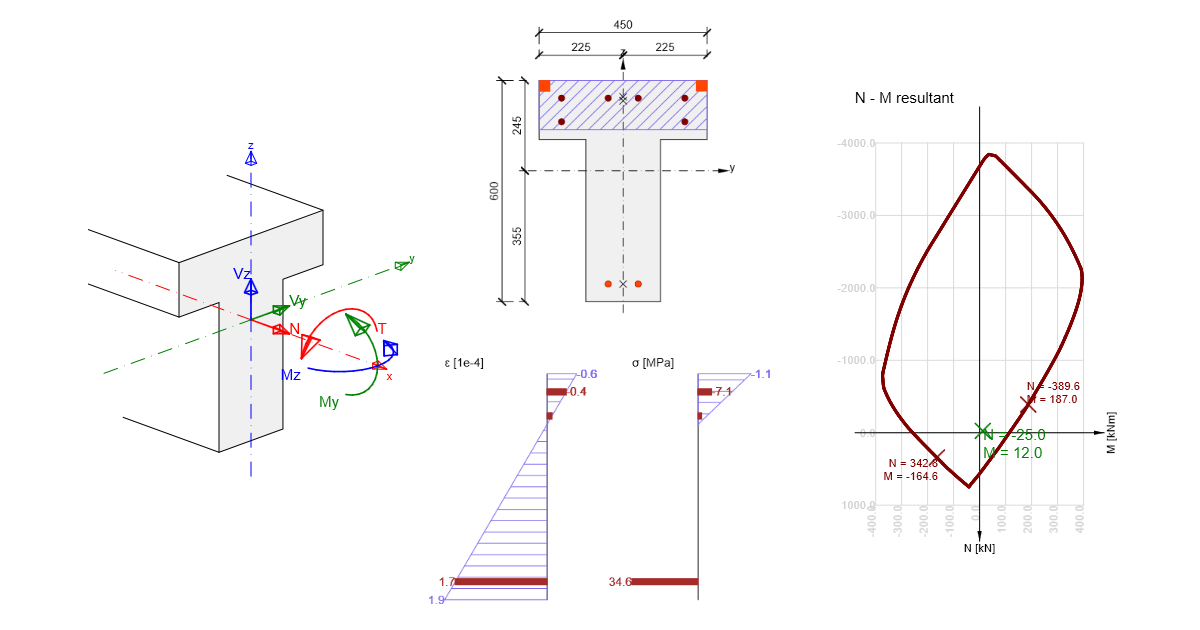
IDEA StatiCa RCS - Dimensionamento estrutural de elementos de betão 1D

Projeto de secções de betão armado segundo as normas EN 1992-1-1 e EN 1992-2.

Flexão
Cisalhamento
Torção
Interação
Verificação da limitação de tensões
Controlo de fissuras
Diagrama N-M-κ
Literatura

Dobragem

Métodos de controlo da capacidade de secção

Dois métodos bem conhecidos podem ser utilizados para verificar o estado limite último para elementos de betão 1D. O primeiro dá-nos a resistência última da secção transversal sob a forma de uma área de interação ou de um diagrama de interação (no caso de momento fletor numa direção).A capacidade da secção transversal pode ser determinada como o rácio entre as forças internas actuantes e as forças do estado limite. A segunda consiste em encontrar o equilíbrio numa secção transversal, onde procuramos o comportamento real da secção carregada, a utilização de materiais em termos de tensões e a perceção das vulnerabilidades da secção.

Pressupostos gerais de projeto e pressupostos de cálculo para o estado limite último

1. A deformação ε na armadura e no betão deve ser assumida como diretamente proporcional à distância ao eixo neutro (as secções planas permanecem planas).
2. A interação entre a armadura e o betão é assegurada pela interação entre o betão e a armadura sem deslizamento (a deformação ε suporta a deformação no betão e as fibras adjacentes são as mesmas).
3. A resistência à tração do betão é negligenciada (todas as tensões de tração são transmitidas pela armadura).
4. As tensões de compressão do betão na zona de compressão são calculadas em relação à deformação calculada a partir dos diagramas tensão-deformação.
5. As tensões da armadura são calculadas em relação à deformação a partir dos diagramas tensão-deformação.
6. Deformação compressiva do betão com um limite de deformação último _εcu2 (diagrama parábola-retângulo para betão sob compressão) e _εcu3 (relação bi-linear tensão-deformação),[2].
7. A deformação de compressão da armadura é ilimitada no caso do ramo superior plástico horizontal, no caso do ramo superior plástico inclinado a deformação é limitada _εud,[2].
8. Um estado limite é considerado quando o estado de pelo menos um dos materiais excede a deformação limite última (se εu não for limitado, o betão comprimido é determinante).

\[ \textsf{\textit{\footnotesize{\qquad Strain stress.}}}\]

\[ \textsf{\textit{\footnotesize{\qquad Diagrama de dimensionamento tensão-deformação para aço de reforço com ramo superior inclinado.}}}\]

Diagrama de interação

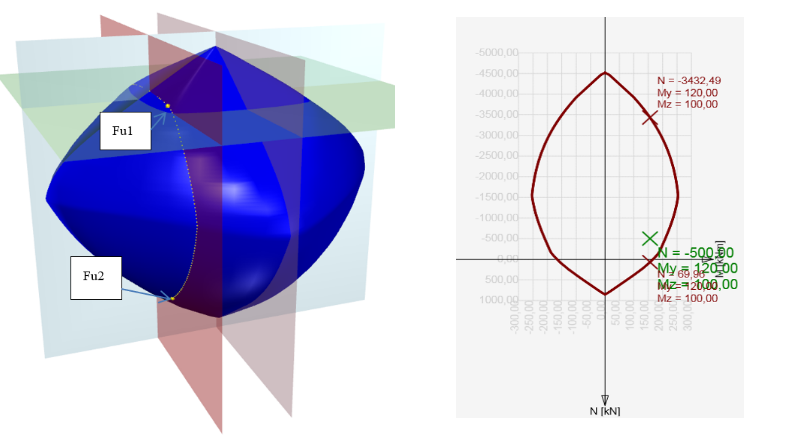
A primeira opção é verificar a secção através de uma superfície de interação (ou diagrama de interação). É fornecida uma explicação sobre uma amostra das superfícies de interação para a secção quadrada reforçada do exemplo na figura abaixo. Na superfície de interação estão localizados pontos que definem o estado limite último da secção examinada.A superfície de interação é desenhada a partir dos pontos (N, My, Mz), que são determinados pela integração de tensões na secção, que atingiu a tensão limite última num dos materiais.Para uma interação 3D, a superfície pode ser derivada de um diagrama de interação 2D, que é uma curva fechada, que corresponde à tensão de um eixo neutro constantemente rodado.

\[ \textsf{\textit{\footnotesize{\qquad Secção reforçada simétrica.}}}\]

\[ \textsf{\textit{\footnotesize{\qquad A superfície de interação mostra as condições de rotura para todos os casos de carga de força normal e momentos fletores.}}}\]

Para o caso de uma secção simétrica em torno do eixo y, o diagrama de interação é simétrico em torno do plano _N-My. De forma idêntica, para o caso de uma secção simétrica em torno do eixo z, o diagrama de interação é simétrico em torno do plano _N-Mz. A secção reforçada unilateral introduz uma forma achatada do diagrama de interação

\[ \textsf{\textit{\footnotesize{\qquad Secção reforçada simétrica simples.}}}\]

\[ \textsf{\textit{\footnotesize{\qquad Superfície de interação para secção com armadura simétrica simples.}}}\]

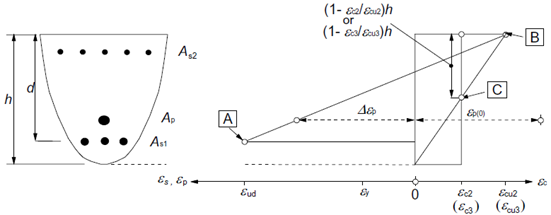
Os pontos que definem o estado limite último são recebidos da integração de tensões. A figura abaixo apresenta a deformação no estado limite último.

Distribuições de deformação no estado limite último (retirado de [2]).

O diagrama de interação mostra a rotura da secção transversal sob força normal e momentos flectores.[1]

Respeitando o problema do diagrama 2D (curva fechada colocada na superfície de interação), podemos descobrir que o plano de deformação passa pelo eixo neutro e pelo ponto crítico [y, z, ε], que é considerado como ponto crítico R. O ponto [y, z] define um ponto na secção transversal com o valor da deformação ε no estado limite último. A inclinação do eixo neutro é constante para todos os pontos do diagrama 2D.

No caso de a tensão de compressão no betão ser crítica para o dimensionamento, o ponto R corresponde à fibra de betão mais comprimida ou ao ponto limite C. No entanto, isto só pode ser aplicado se essa secção for feita de um tipo de betão - não como uma secção transversal mista.

No caso de a tensão de tração na armadura ser crítica para o dimensionamento (a deformação _εud é excedida no estado limite último para um ou mais varões), deve ser cumprida a condição de que, para o plano de deformação dado, o valor _εud não é excedido em nenhum outro varão.

\[ \textsf{\textit{\footnotesize{\qquad Utilização óptima do material da secção}}\]

\[ \textsf{\textit{\footnotesize{\qquad Posições do plano de deformação caraterístico calculadas para efeitos do diagrama de interação.}}\]

A imagem acima mostra que o diagrama pode ser dividido em duas partes: a parte em que a falha é causada por uma força de tração e a parte que falha por uma força de compressão.Os pontos limite correspondem ao caso acima, onde também se pode ver a inclinação extrema do plano de deformação.Ao desenhar um diagrama de interação, a inclinação do plano de deformação de uma secção transversal está a mudar neste intervalo, enquanto procuramos o ponto R (ver acima). Com base nesse plano definido, efectuamos a integração para obter a tensão no estado limite último.

Secção transversal sujeita a força axial e verificação do momento fletor

A verificação de uma secção transversal sujeita a força axial e momento fletor baseia-se em provar que as tensões verificadas (combinação _Nd,_Myd, _Mzd) estão localizadas dentro ou na área de interação da superfície. O exemplo seguinte demonstra a verificação de uma secção retangular sujeita a forças Nd₌ -500 kN,_Myd = 120 kNm, _Mzd = 100 kNm.

Método NuMuMu

Para definir a resistência de uma secção transversal, assumimos alterações proporcionais em todas as componentes da força interna (a excentricidade da força normal permanece constante) até que a superfície interactiva tenha sido desenvolvida.A alteração das forças internas envolvidas pode ser interpretada como um movimento ao longo de uma linhaque liga o sistema de coordenadas inicial (0,0,0) e o ponto definido pelas forças internas (_NEd,_MEd,y,_MEd,z).As duas intersecções desta linha com a superfície de interação, que podem ser encontradas, representam dois conjuntos de forças no estado limite último. Em cada intersecção, o programa determina três forças no estado limite: a resistência da força axial de cálculo_NRd e os correspondentes momentos de resistência de cálculo_MRdy,_MRdz.

Método NuMM

Para definir a resistência da secção transversal, assumimos uma força normal constante (que é igual à força normal de cálculo atuante) e alterações proporcionais nos momentos fletores até que a superfície interactiva tenha sido desenvolvida.A variação das forças internas envolvidas pode ser interpretada como um movimento num plano horizontal ao longo da linha que liga o ponto (_NEd,0,0) e o ponto definido pelas forças internas actuantes (_NEd,_MEd,y,_MEd,z).As duas intersecções desta linha com a superfície de interação, que pode ser encontrada, representam dois conjuntos de forças no estado limite último. Em cada intersecção, o programa determina três forças no estado limite: os momentos resistentes de dimensionamento_MRdy,_MRdz e a força normal de dimensionamento (correspondente) atuante_NEd.

Método NMuMu

Para definir a resistência da secção, assumimos uma força normal constante (que é igual à força normal de cálculo atuante) e alterações proporcionais nos momentos fletores até que a superfície interactiva tenha sido desenvolvida.A alteração das forças internas envolvidas pode ser interpretada como um movimento num plano horizontal ao longo da linha que liga o ponto (_NEd,0,0) e o ponto definido pelas forças internas actuantes (_NEd,_MEd,y,_MEd,z).As duas intersecções desta linha com a superfície de interação, que podem ser encontradas, representam dois conjuntos de forças no estado limite último. Em cada intersecção, o programa determina três forças no estado limite: os momentos resistentes de dimensionamento_MRdy,_MRdz e a (correspondente) força normal de dimensionamento atuante_NEd.

Determinação da resposta da secção

Outra possibilidade de verificar a secção transversal é encontrar a resposta da secção transversal (ou seja, a distribuição de deformação e tensão das forças internas actuantes). Este método também é conhecido como o método da deformação limite.O nível de tensões actuantes em cada fibra (no caso de flexão plana em cada camada) emCada barra reforçada é calculada em função da tensão do diagrama tensão-deformação do material.
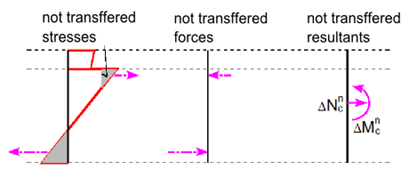
A determinação da resposta da secção transversal é calculada utilizando o método numérico especificado em[6]. O princípio consiste no aumento gradual da carga da secção através dos componentes desequilibrados das forças não transferidas, que são obtidos através da integração da tensão sobre a secção utilizando diagramas tensão-deformação.Se o valor da tensão puder ser encontrado para a deformação no diagrama tensão-deformação, ver Figura abaixo (a), a tensão calculada está correta, assumindo um material elástico linear.Nos casos (b) e (c), a tensão para um cálculo linear atinge valores irrealistas, e parte (b) ou todo o valor (c) não pode ser transmitido pelo material. Integrando as tensões não transferidas, obtemos forças internas não transferidas, e as suas resultantes devem ser adicionadas às forças internas de cargas variáveis.

Tensões não transferidas em diagramas tensão-deformação [4].

Forças internas não transferidas.[4]

Este método de cálculo requer a utilização de métodos numéricos para integrar a tensão sobre a área da secção transversal e para a análise não linear das equações de equilíbrio na secção. A iteração é terminada no momento em que os critérios de convergência são cumpridos.

\[\frac{{F_e} - {F_i}}}{{{F_e}}} \le max\left\{ {e,d} \right\}\]

em que

_{Fe é a} carga da secção,

_{Fi é a} resposta da secção (forças internas calculadas na base do plano de deformação).

Se a é o valor aproximado (aproximado) e b é o valor exato (verdadeiro), então o desvio absoluto é dado pela seguinte equação.

\[e = \left| {b - a} \right|\]

O desvio relativo é dado pela seguinte fórmula:

\[d = \left| {\frac{{b - a}}}{b}} \right|\]

Na maioria dos programas, é possível definir estes critérios de convergência (os valores predefinidos são 1%como erro relativo, 100 N, 100 Nm como erro absoluto da força normal e dos momentos).

Assim, se tivermos a entrada de N = 0 kN, My = 100 kNm, Mz= 0 kNm e as forças integradas após a iteração N = - 0.07 kN, My = 100,5 kNm, Mz = 0,02 kNm, a avaliação será a seguinte. Respeitando o facto de N e Mz serem iguais a 0, pode ser feita uma comparação com o desvio absoluto:

O valor da força normal 100N> | 70 | N
O valor do momento fletor Mz 100Nm> | 20 | Nm
O valor do momento fletor My

\[d = \left| {\frac{{b - a}}{b}} \direita| = \frac{{100 - 100,5}}{{{100}} = 0,005\; < 0,01\]

Verificação da secção transversal pela resposta

No caso de encontrar um equilíbrio na secção, a deformação plana é conhecida.A partir da deformação plana, podemos calcular a deformação em qualquer parte da secção e, em seguida, a tensão ou as forças internas nas barras de reforço, na secção ou nas suas partes utilizando diagramas de tensão-deformação dos materiais. Os valores de tensão e deformação calculados são comparados com o valor de deformação limite dos diagramas de tensão-deformação dos materiais utilizados.
A vantagem deste método é que obtemos uma imagem completa dos valores de tensão e deformação na secção das forças internas que actuam na secção transversal.

Cisalhamento

No que diz respeito à rotura frágil, a verificação do corte é uma das verificações importantes de uma secção de betão armado.

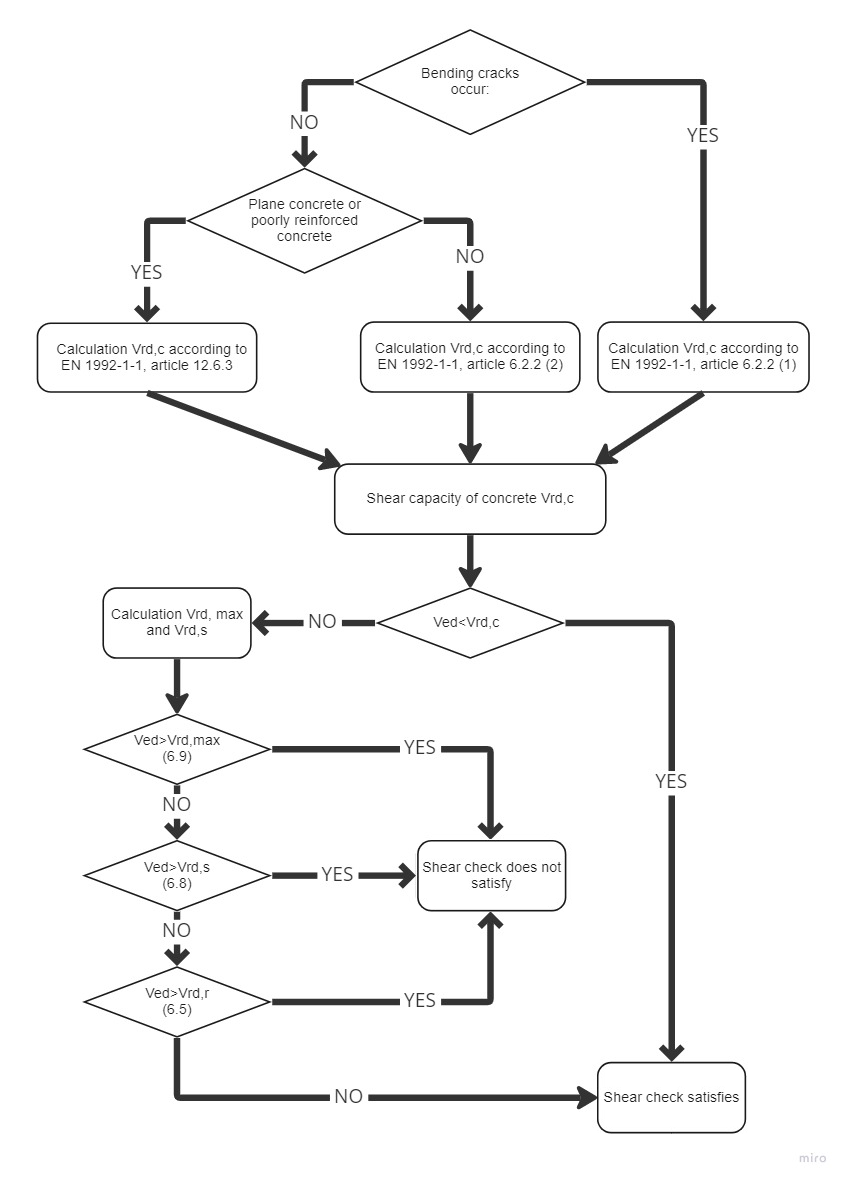
Procedimento de cálculo

O cálculo da resistência ao cisalhamento é composto por várias partes básicas. Em primeiro lugar, deve-se analisar se as fissuras devidas à flexão ocorrem ou não no local verificado.Se existirem, utiliza-se o cálculo de acordo com a EN 1992-1-1[2], Artigo 6.2.2 (1).Caso contrário, determina-se se se trata de betão plano ou de betão mal armado e, em seguida, procede-se de acordo com a norma EN 1992-1-1, artigo 12.6.3.

No caso do betão armado não fissurado (sem armadura de corte), procede-se à verificação de acordo com a norma EN 1992-1-1, artigo 6.2.2 (2) Para Elementos, onde é necessária uma armadura de cisalhamento, verificamos de acordo com o Artigo 6.2.3[2].

\[ \textsf{\textit{\footnotesize{\qquad Diagrama de processo para verificação de corte.}}\]

Resistência ao corte de barras sem armadura de corte

Resistência ao corte de barras em zonas de flexão fendilhadas (art. 6.2.2 (1)[2])

A resistência ao corte de elementos de betão armado sem armadura de corte sujeitos a momento fletor é dada por

\[{{V}_{Rd,cm}}=~{{C}_{Rd.c}}k~{{\left( 100~{{\varrho }_{l}}{{f}_{ck}} \right)}^{{}^{1}/{}_{3}}}~{{b}_{w}}d\]

A qual foi definida com base em ensaios efectuados num número representativo de vigas simples em caso de rotura por força de corte. Uma vez que a resistência acima pode ser nula para elementos sem armadura longitudinal (_rl), para elementos mal armados foram derivadas equações. Uma vez que a resistência acima pode ser nula para elementos sem armadura longitudinal (_rl), para os elementos mal armados foi determinada pela equação

\[{{V}_{Rd,c}}\ge ~{{\upsilon }_{min}}{{{b}_{w}}d\]

Para a resistência ao corte com influência da força normal foi determinada pela equação

\[{{V}_{Rd,cn}}=~{{k}_{1}}{{\sigma }_{cp}}~{{b}_{w}}d\]

Resistência ao corte na sua expressão completa que corresponde à EN 1992-1-1 art. 6.2.2 (1)

\[{{V}_{Rd,c}}=~\left[ {{C}_{Rd.c}}k~{{\left( 100~{{\varrho }_{l}}{{f}_{ck}} \right)}^{{}^{1}/{}_{3}}}+{{{k}_{1}}{{\sigma }_{cp}} \right]~{{b}_{w}}d\]

Com o mínimo de

\[{{V}_{Rd,c}}=~\left( {{\upsilon }_{min}}+{{k}_{1}}{{\sigma }_{cp}} \right){{b}_{w}}d\]

em que

_CRd,c = 0,18 / _γc,

k fator de altura da secção transversal

\[k=1+\sqrt{\frac{200}{d}}<2,0\]

_ρ1 taxa de armadura para armadura longitudinal

\[{{\varrho }_{l}}=\frac{{{A}_{sl}}}{{{b}_{w}}d}\le 0,02\]

_fck resistência caraterística à compressão cilíndrica do betão aos 28 dias

_k1 = 0,15

_σcp =_NEd /_Ac < 0,2 _fcd v MPa

_bw largura mais pequena da secção transversal na zona de tração

d profundidade efectiva de uma secção transversal

_υmin resistência mínima ao cisalhamento equivalente _υmin = 0,035 ^{k3/2 fck1/2}

Resistência ao corte de barras em zonas de flexão não fendilhadas (art. 6.2.2 (2)[2])

A resistência ao corte de barras em zonas de flexão não fendilhadas pode ser determinada a partir do círculo de Mohr. Na equação

\[{{\sigma }_{1,2}}=\frac{{{\sigma }_{x}}+{{\sigma }_{y}}}}{2}\pm \sqrt{{{\left( \frac{{\sigma }_{x}}-{{\sigma }_{y}}}}{2} \right)}^{2}}+\tau _{z}^{2}}\]

Substituímos _σx = _σcp a τz₌ VRd_,c S / (I _bw) e calculamos VRd_,c e obtemos a equação correspondente à fórmula dada na EN 1992-1-1 art. 6.2.2 (2)

em que

I é o segundo momento da área,

_bw é a largura da secção transversal no eixo centroidal

S é o primeiro momento da área acima e em torno do eixo centróide,

_fctd resistência à tração axial de projeto do betão, em MPa,

_scp é a tensão de compressão do betão no eixo centroidal devida à carga e/ou ao pré-esforço,

_al fator de comprimento de transmissão, geralmente 1,0.

Em relação ao que precede, deve notar-se que, em zonas sem fissuras de flexão, aresistência VRd_,c pode ser significativamente mais elevada do que nas zonas fissuradas, de acordo com o artigo 6.2.2 (1)[2]. A figura abaixo mostra claramente que, embora a força de corte seja verificada no seu extremo (o que não produz fissuras), não precisa necessariamente de garantir que será transferida ao longo de todo o comprimento da viga.Isto deve-se a uma alteração no método de cálculo da resistência ao corte do betão.Por segurança, é claro que a resistência ao cisalhamento pode ser considerada de acordo com o Artigo 6.2.2 (1)[2] também em locais onde não ocorrerão fissuras.

\[ \textsf{\textit{\footnotesize{\qquad Comparação da resistência ao corte antes e depois da ocorrência de fendas.}}}\]

Para a expressão de VRd_{, c} de acordo com o Artigo 6.2.2 (2)[2] também deve ser notado que, no caso geral, deve ser baseado na verificação na fibrada tensão de tração principal extrema do betão na zona de tensão de compressão normal, mas não no centro de gravidade da secção.Nesta altura, é necessário calcular as caraterísticas da secção transversal (S e _bW).Para determinar a tensão principal máxima _s1 no programa IDEA RCS, traçamos uma linha através do centro de gravidade na direção das forças de corte resultantes.Esta linha é dividida em 20 sectores e nesta linha serão apresentados mais pontos caraterísticos (pontos do polígono da secção transversal, centro de gravidade, eixo neutro).Dentro destes pontos, calculamos S, _bw, _σx, _τyz a σ1_. No ponto de tensão de tração principal máxima, calcula-se a resistência ao corte.

A força de corte antes de aplicar o fator de redução b requerido pelo Artigo 6.2.2 (6) deve satisfazer a condição extra

\[ {{V}_{Ed}}\le 0,5~{{b}_{w}}d~\upsilon ~{{f}_{cd}}\]

em que

\ [ {{ υ}}\le 0,6\left[ 1-\frac{{{f}_{ck}}}{250} \right]\] kde _fck je v MPa

Resistência ao corte de barras sem armadura ou ligeiramente armadas (art. 12.6.3[2])

A resistência ao corte para betão simples ou ligeiramente armado pode ser determinada a partir da expressão

\[ {{\tau }_{cp}}\le k~{{V}_{Ed~}}/{{{A}_{cc}}\]

Onde

_τcp substituímos por

\[ {{f}_{cvd}}=\sqrt{f_{ctd,pl}^{2}+{{\sigma }_{cp}}{{f}_{ctd,pl}}}~pro~{{\sigma }_{cp}}\le {{\sigma }_{c,lim}}~\]

ou

\[ {{f}_{cvd}}=\sqrt{f_{ctd,pl}^{2}+{{{\sigma }_{cp}}{{f}_{ctd,pl}}-{{\left( \frac{{\sigma }_{cp}}-{{\sigma }_{c,lim}}}}}{2} \right)}^{2}}}~pro~{{\sigma }_{cp}}>{{{\sigma }_{c,lim}}~\]

Os valores parciais utilizados na fórmula acima são dados por:

\[ {{\sigma }_{c,lim}}={{f}_{cd,pl}}-2\sqrt{{f}_{ctd,pl}}\left( {{f}_{ctd,pl}}+{{f}_{cd,pl}} \right)}\]

em que

fcd_,pl Resistência à compressão de projeto para betão simples ou ligeiramente armado,

fctd_,pl Resistência à tração axial de projeto do betão simples ou ligeiramente armado,

_fcvd Resistência ao corte de projeto sob compressão do betão.

A resistência dos elementos com armadura de corte (art. 6.2.3[2])

O cálculo da resistência das barras de betão armado com armadura de corte é baseado no método da analogia da treliça com diagonais de ângulo variável.A base deste método é o equilíbrio de forças no triângulo determinado pela força da escora (diagonal), a força da armadura de corte (estribo) e a força da armadura longitudinal.

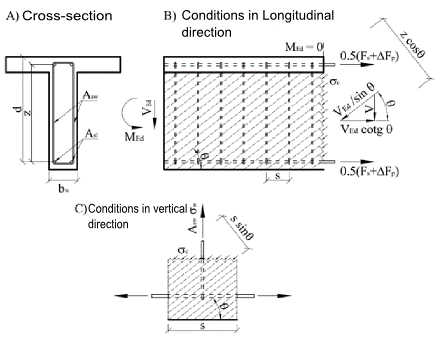
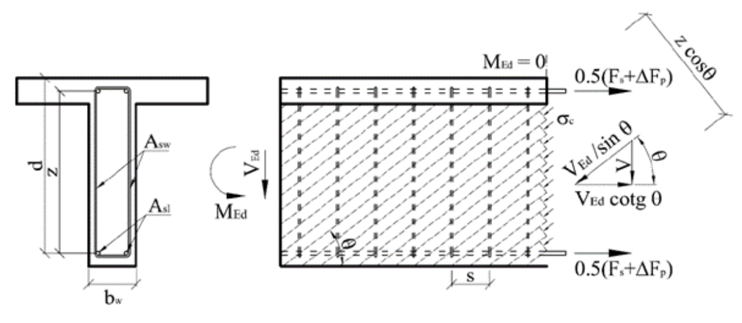
\[ \textsf{\textit{\footnotesize{\qquad Principe of Truss analogy for member under shear load.}}}\]

A secção transversal sob carga de corte é quebrada por fendas num ângulo θ, por esta razão a diagonal de betão com o mesmo ângulo que as forças de corte resiste à força de corte. A força de compressão da diagonal pode ser expressa como _Ved/sinθ. Esta força deve ser transferida pela superfície do betão, perpendicular à diagonal de compressão _bwzcosθ. A tensão de tração do betão na diagonal de compressão é então igual:

\[ {{\sigma }_{c}}=\frac{{{V}_{Ed}}}{{{b}_{w}}z~\sin \text{ }\!\!\theta\!\!\text{ }\cos \theta }=\frac{{V}_{Ed}}}{{{b}_{w}}z}\left( \tan \theta +\cot \theta \right)\]

Substituindo \ [{{\sigma }_{c}}={{{\alpha }_{cw}}{{\nu }_{1}}{{{f}_{cd}}\] e \ [{{V}_{Ed}}={{{V}_{Rd,max}}\] e expressando \ [{{V}_{Rd,max}}\] obtemos a equação para a resistência ao corte da diagonal:

\[ {{V}_{Rd,max}}=~{{\alpha }_{cw}}~{{b}_{w}}~z~{{\nu }_{1~}}{{f}_{cd}}/\left( \cot \theta +\tan \theta \right)\]

Para equilibrar a componente da força vertical na diagonal de compressão, será utilizada uma armadura de corte.A dimensão da força vertical é baseada na tensão de compressão diagonal na área de betãoárea de betão que corresponde a um único estribo - \ [{{\sigma }_{c}}{{{b}_{w}}s{{\sin }^{2}}\theta\]. A força limite do estribo é dada como \ [{{A}_{sw}}{{{f}_{ywd}}/s\].

Inserindo _σc, comparando com a força limite na armadura, após modificações obtemos:

\[ \frac{{{A}_{sw}}{{f}_{ywd}}}{s}=\frac{{{V}_{Ed}}}{z}\tan \theta\]

Em seguida, expressando _Ved como _VRDs, obtemos a resistência da secção com armadura de corte vertical:

\[ {{V}_{Rd,s}}=~\frac{{{A}_{sw}}}{s}z~{{f}_{ywd}}\cot \theta\]

A força de corte longitudinal é transferida pela armadura longitudinal e pode ser determinada como _Vedcotgθ. A derivação das fórmulas acima pode ser encontrada em[4].

Utilizando o programa IDEA RCS, é possível verificar apenas barras com armadura de corte vertical. Em geral, podem ser utilizadas as seguintes equações:

\[{{V}_{Rd,s}}=~\frac{{{A}_{sw}}}{s}z~{{f}_{ywd}}\left( \cot \theta +\cot \alpha \right)\sin \alpha\]

\[{{V}_{Rd,max}}=~{{\alpha }_{cw}}~{{b}_{w}}~z~{{\nu }_{1~}}{{f}_{cd}}\left( \cot \theta +\cot \alpha \right)/\left( 1+{\cot }^{2}}\theta \right)\]

Em que

_Asw é a área da secção transversal da armadura de corte,

s é o espaçamento dos estribos,

_fywd é a tensão de cedência de projeto da armadura de corte,

_bw é a largura mínima entre as cordas de tração e de compressão. Para calcular a resistência VRd_,max , o valor da largura da secção deve ser reduzido para a chamada largura nominal da secção transversal, no caso de a secção transversal ser enfraquecida por condutas de cabos

bw_,nom=bw-0,5ΣΦ para condutas metálicas betumadas

bw_,nom=bw-1,2ΣΦ para condutas metálicas não betumadas

υ = 0,6 pro _fck ≤ 60MPa ou pro _fck > 60MPa,

_αcw é um coeficiente que tem em conta o estado da tensão na corda de compressão.

Carga	σcp = 0	0 <σcp≤0,25fcd	0,25fcd <σcp≤0,5fcd	0,5fcd <σcp≤1,0fcd
Coeficienteacw	1,0	1+σcp/fcd	1,25	2,5(1 - σcp/fcd)

Tab. 1-1 Coeficiente de determinação _αcw

O ângulo θ é o ângulo entre a escora de compressão do betão e o eixo da viga perpendicular à força de corte. Os valores limite de cotθ para utilização num país podem ser consultados no respetivo Anexo Nacional. Os limites recomendados são dados pela expressão:

\[1~\le ~\cot \theta \le 2,5\]

A escolha do tamanho do ângulo θ pode afetar o valor das resistências. A dependência das resistências é visível na Figura 1.15 A figura mostra que, com o aumento do ângulo θ, a resistência VRd_,max aumenta e a resistência VRd_,s diminui. A resistência VRd_,c é constante, uma vez que se baseia no método da analogia da treliça.

\[ \textsf{\textit{\footnotesize{\qquad Dependência entre a resistência ao corte e o ângulo q.}}}\]

Cálculo das caraterísticas da secção para o corte

Para calcular o corte, é importante calcular as variáveis da secção que afetam a resistência ao corte.Estas variáveis incluem principalmente a largura da secção resistente ao corte _bw, a profundidade efetiva d e o braço de alavanca z. O código[2] fornece estes valores que se correlacionam diretamente com a tensão de flexão real.Mas o problema é determinar estes valores quando a direção dos momentos flectores resultantes (ou mais precisamentea direção da resultante da resistência da secção) é significativamente diferente da direção das forças de corte resultantes.Neste caso, o código EC2 não fornece quaisquer recomendações.

Largura da secção transversal que resiste ao corte _bw

O programa IDEA RCS calcula a largura da secção transversal resistente ao corte na direção perpendicular à resultante das forças de corte.Dependendo do artigo do Eurocódigo, esta largura é calculada como
- A menor largura da secção entre a resultante de compressão do betão e a armadura de tração na direção perpendicular à resultante das forças de corte para o artigo 6.2.2 (a) e 6.2.3 (1)
- A largura da secção numa direção perpendicular à resultante das forças de corte no ponto verificado de acordo com o artigo 6.2.2 (2)

Profundidade efectiva de uma secção transversal

A profundidade efectiva é normalmente definida como a distância da fibra de betão mais comprimida ao centro de gravidade da armadura.Uma vez que está diretamente relacionada com a flexão, a distância é dada como projeção perpendicular à linha de gravidade da deformação plana.

Esta definição pode ser clarificada de modo a que, em vez do centro de gravidade da armadura de tração, seja utilizada a posição da resultante das forças da armadura.Durante o desenvolvimento do programa IDEA RCS, o problema foi resolvido:como definir a profundidade efectiva da secção transversal, para a qual o plano das cargas de flexão não corresponde à direção das forças de corte resultantes.Assim, a profundidade efectiva é definida como a distância da fibra de betão mais comprimida às forças resultantesna armadura de tração (com base na tensão de flexão) e na direção das forças de corte resultantes, ver Figura 1.17.

Casos excepcionais ocorrerão se não for possível determinar a fibra comprimida ou a resultante na armadura de tração. Neste caso, recomenda-se a utilização do valor 0.9 h (90% da profundidade da secção na direção das forças de corte resultantes). Este valor pode ser definido pelo utilizador no programa IDEA RCS através da definição de variáveis de código.

Braço de alavanca das forças internas

O braço de alavanca das forças internas está em 6.2.3 (3)[2] e é definido como a "distância entre as cordas de tração e compressão". A norma não define como proceder quando o plano do momento fletor atuante é diferente da direção das forças de corte resultantes.Portanto, como no caso da profundidade efectiva, definimos a distância na direção das forças de corte resultantes.Também aqui, podemos enfrentar casos de exceção semelhantes, por exemplo, toda a secção está sob compressão, etc. Neste caso, tomamos o valor 0,9 d (90% da altura efectiva da secção). Este valor, o utilizador pode definir no programa IDEA RCS através da definição de variáveis de código.

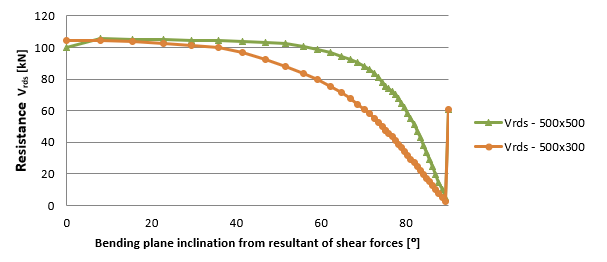
A dependência entre a inclinação do plano de flexão e a resultante da força de corte é claramente visível na Figura 1.18 e na Figura 1.19.19. Com o aumento da inclinação, os valores da altura efectiva, dos braços de alavanca e das resistências relacionadas diminuem. O estado limite é 90°. Para esta inclinação, o braço de alavanca das forças internas não pode ser calculado, pelo que o braço de alavanca é igual a zero. Neste caso, é considerado o valor especificado na definição das variáveis de código. Desta forma, existe um salto no final do gráfico. Este estudo prova que o máximo recomendado para a inclinação é de cerca de 20°.

\[ \textsf{\textit{\footnotesize{\qquad Dependência entre a profundidade efectiva, o braço de alavanca para a inclinação do plano de flexão e a resultante das forças de corte.}}}\]

\[ \textsf{\textit{\footnotesize{\qquad Dependência entre a resistência Vrds para a inclinação do plano de flexão e a resultante do corte.}}}\]

Como parte dos testes da aplicação RCS, foi realizado um estudo sobre a dependência da resistência ao corte com a alteração da força normal. A resistência VRd_,max é afetada apenas pelo coeficiente _αcw, ver Fig. 1.20. 1.20. A Fig. 1.21 mostra um valor constante da resistência _VRds. Para a resistência _VRdc, as diminuições causam o aumento da força normal.A curva azul da Fig. 1.21 mostra a resistência _VRdc, negligenciando a influência das fissuras, e foi calculada utilizando a fórmula da secção 6.2.2 (1)[2] O salto na transição entre pressão e tração é causado pela contribuição da armadura de tração. A curva vermelha é calculada utilizando a fórmula da secção 6.2.2 (2)[2]. Após a ocorrência da primeira fissura, a curva de dependência é a mesma que para 6.2.2 (1)[2].

\[ \textsf{\textit{\footnotesize{\qquad Curva de dependência da resistência ao corte VRd,max para a força normal.}}}\]

\[ \textsf{\textit{\footnotesize{\qquad Dependência das resistências ao corte VRd,c a VRd,s em relação à força normal.}}}\]

Torção

Pressupostos de cálculo

O comportamento de uma secção de betão armado sujeita a torção pode ser dividido em duas categorias - antes e depois do momento em que se espera que as fissuras ocorram pela primeira vez. Antes de uma fissura, a secção transversal comporta-se como um material elástico. A tensão de torção pode ser expressa pela fórmula

\[\tau =~\frac{{{T}_{Ed}}}{{{W}_{t}}}\]

onde _Wt je módulo seccional em torção.

As fendas na barra não reforçada devido à tensão de torção principal são também o estado limite último. O comportamento de uma secção de betão armado sujeita a torção pode ser descrito com base numa secção fechada de parede fina, ver Fig. abaixo.

\[ \textsf{\textit{\footnotesize{\qquad Secção de parede fina equivalente.}}}\]

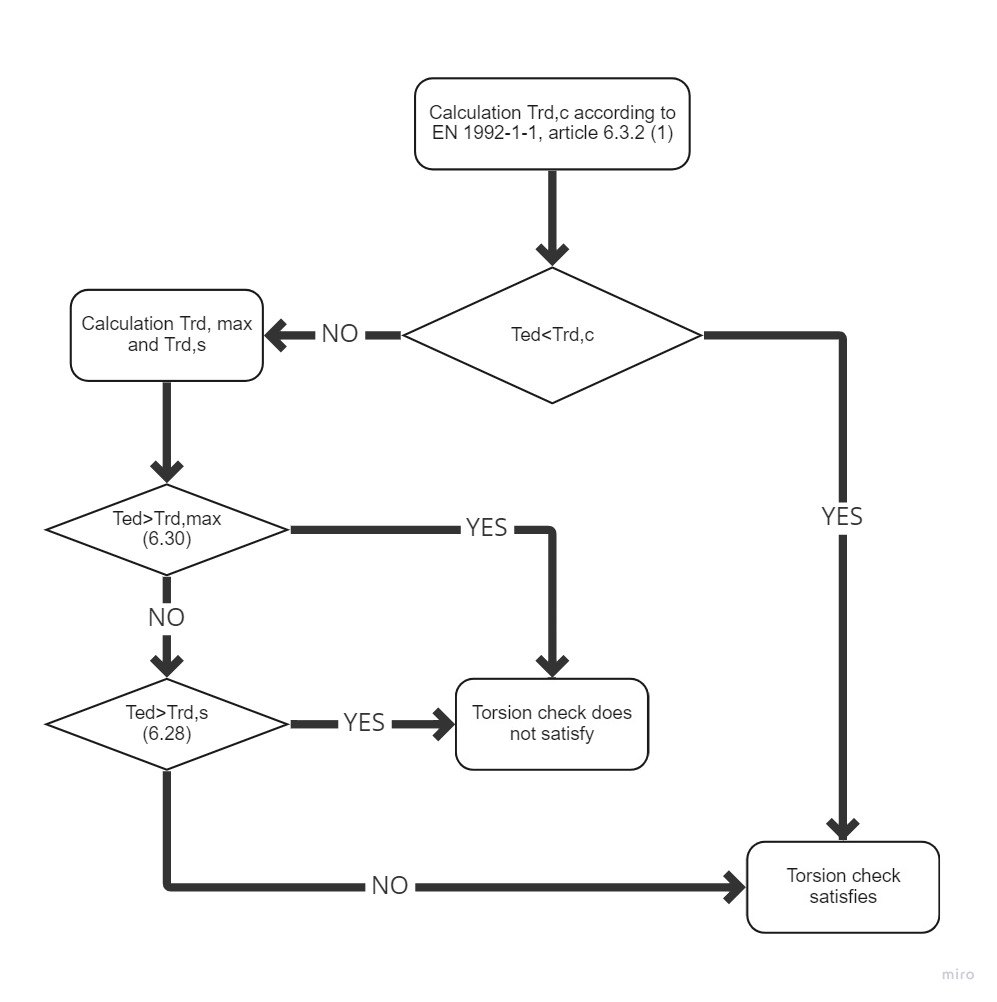
Procedimento de cálculo

O processo de uma verificação de betão armado para torção é muito semelhante à verificação para corte. Em primeiro lugar, verificamos a resistência do betão.Se a verificação do betão for satisfeita, a armadura pode ser dimensionada utilizando as regras de pormenorização. Caso contrário, é necessário verificar a armadura e a resistência diagonal à compressão através do cálculo.

\[ \textsf{\textit{\footnotesize{\qquad Diagrama de processo para verificação de torção.}}}\]

Resistência

O fluxo de corte numa parede de uma secção de parede fina sob torção pode ser expresso como:

\[ {{\tau }_{t}}{{t}_{ef}}=~\frac{{{T}_{Ed}}}}{2{{A}_{k}}}\]

A força de corte numa parede de uma secção transversal de parede fina pode ser expressa como:

\[ V={{\tau }_{t}}{{{t}_{ef}}z\]

Onde

τ Fluxo de cisalhamento na parede,

_tef é a espessura efectiva da parede,

z é o comprimento lateral da parede,

_TEd é o momento de torção,

_Ak é a área delimitada pelas linhas centrais das paredes de ligação, incluindo as áreas ocas interiores.

Momento de torção de fendilhação, que pode ser determinado ajustando _fctd à expressão anterior. Assim, obtém-se a expressão para a resistência à torção sem armadura de torção.

\[ {{T}_{Rd,c}}=2{{A}_{k}}{{t}_{ef}}{{f}_{ctd}}\]

onde _fctd resistência à tração axial de projeto do betão

\[ \textsf{\textit{\footnotesize{\qquad Principles of Truss analogia para membro sob momento de torção.}}}\]

A resistência da barra com armadura de torção é composta a partir da resistência das diagonais de betão à compressão, que se baseia novamente no método de analogia de treliça. A tensão de compressão na diagonal pode ser expressa com a ajuda da força de corte na parede de uma secção de parede fina na superfície da parede que está em consideração, ou seja

\[{{\sigma }_{c}}=\frac{\frac{{{T}_{Ed}}z}{2{{A}_{k}}\sin \theta }}{z~{{t}_{ef}}\cos \theta }=\frac{{{T}_{Ed}}}{2{{A}_{k}}{{{t}_{ef}}\sin \theta \cos \theta }\]

Substituindo _σc=σcwfcd e_TEd=TRd,max e expressando_TRd,max obtemos uma equação para a resistência diagonal à compressão

\[{{T}_{Rd,max}}=2~\nu ~{{\alpha }_{cw}}~{{f}_{cd}}~{{A}_{k}}~{{t}_{ef~\sin \theta ~\cos \theta }}\]

em que

ν = 0,6 para _fck ≤ 60MPa ou para _fck > 60MPa

Coeficiente _αcw que tem em conta o estado de tensão de compressão na corda de compressão

_fcd valor de projeto da resistência à compressão do betão

a resistência da armadura de corte sujeita a torção é novamente baseada na tensão na diagonal de compressão. A força do estribo é igual à tensão na diagonal comprimida na área que corresponde à linha de estribo específica, ou seja

\[{{A}_{sw}}{{f}_{ywd}}=\frac{{{T}_{Ed}}}}{2{{A}_{k}}{{{t}_{ef}}\sin \theta \cos \theta }~{{t}_{ef}}~s{\sin }^{2}}\theta =\frac{{{T}_{Ed}}}~s}{2{{A}_{k}}\cot \theta }~\]

Substituindo_TEd=TRd,s e exprimindo_TRd, s obtemos a equação:

\[{{T}_{Rd,s}}=2{{A}_{k}}\frac{{{A}_{sw}}{{f}_{ywd}}}{s}~\cot \theta\]

Se a quantidade de armadura longitudinal e de corte for conhecida, podemos definir o ângulo θ através da expressão

\[{{\tan }^{2}}\theta =\frac{\frac{{{A}_{sw}}{{f}_{ywd}}}{s}}{\frac{{{A}_{sl}}{{f}_{yd}}}{{{u}_{k}}}}\]

Substituindo por_TRd,s obtemos

\[{{T}_{Rd,s}}=2{{A}_{k}}\sqrt{\frac{{{A}_{sw}}}{s}{{f}_{ywd~}}\frac{{{A}_{sl}}}{{{u}_{k}}}~{{f}_{yd}}}\]

Onde

_Asw área de armadura de corte

s é o espaçamento radial dos estribos da armadura de cisalhamento

_fywd é a resistência efectiva de projeto da armadura de corte

_Asl área da armadura longitudinal

_uk é o perímetro exterior da secção transversal

_fywd é a resistência efectiva de projeto da armadura longitudinal

A força na armadura longitudinal pode ser deduzida da força de corte numa parede de uma secção sujeita a um momento de torção puro, que é dada como

\[V=\frac{{{T}_{Ed}}}{2{{A}_{k}}}{{u}_{k}}\]

Essa força é transformada para a direção longitudinal e obtemos:

\[{{F}_{l}}=\frac{{{T}_{Ed}}{{u}_{k}}}{2{{A}_{k}}~\tan \theta }\]

O intervalo permitido dos valores para o ângulo θ é semelhante ao da verificação de cisalhamento, ou seja, 1 < cot θ < 2,5. A dependência entre as resistências pode ser vista na Fig. abaixo. O diagrama mostra que com o aumento do ângulo θ a resistência_TRd,max está a aumentar, a resistência_TRd.s está a diminuir e a resistência_TRd,c é constante, uma vez que não se baseia no método de analogia de treliça.

\[ \textsf{\textit{\footnotesize{\qquad Závislost únosnosti průřezu v kroucení na úhlu θ.}}}\]

Cálculo das caraterísticas da secção transversal para torção

Para verificar a secção transversal para torção, é necessário estabelecer uma chamada secção fechada de parede fina equivalente. Para determinar as dimensões da secção transversal de parede fina equivalente, assumindo uma forma retangular.Para a área real dos estados rectangulares A = b×h e para a circunferência do retângulo u =2 (b +h).A utilização destas duas equações pode fornecer uma área alternativa em forma de retângulo fino e a periferia da secção transversal original. Resolvendo duas equações com duas incógnitas, obtemos

\[b=\frac{-u\pm \sqrt{{{u}^{2}}-16A}}{-4}\text{ }\!\!~\!\!\text{ }\]

\[h=\frac{\left( u-2\text{b} \right)}{2}\]

A espessura da parede da secção transversal efectiva pode ser definida a partir da periferia e da área da secção como:

\[t=\text{A}/\text{u}\]

Em seguida, a área e a periferia definidas pela linha central da secção efetiva:

\[{{A}_{k}}=\left( \text{h}-\text{t} \right)\text{ }\!\!~\!\!\text{ }\left( \text{b}-\text{t} \right)\text{ }\!\!~\!\!\text{ }\]

\[{{u}_{k}}=2\left( \left( \text{h}-\text{t} \right)+\text{ }\!\!~\!\!\text{ }\left( \text{b}-\text{t} \right) \right)\]

O problema com este método é para secções transversais do tipo T com uma placa larga quando a área total e a periferia são consideradas para calcular as dimensões (incluindo esta placa).Nas versões futuras do programa IDEA RCS, será permitida a seleção da parte da secção mais maciça, que será utilizada para verificar a torção.

Interação

Interação da força de corte e da torção para armaduras de corte

Determinação da força na armadura de corte devido à força de corte.

O cálculo baseia-se na fórmula de cálculo da resistência da armadura de corte definida na EN 1992-1-1. Com base na equação 6.13 (cap. 6.2.3 (4)), a resistência à carga de uma perna de estribo pode ser derivada como:

\[{{V}_{Rd,s}}=\frac{{{A}_{sw,V}}}{s}z{{{f}_{ywd}}\left( \cot \theta +\cot \alpha \right)\sin \alpha \cos \beta \]

\[\frac{{{A}_{sw,V}}}{s}={{a}_{sw,V}}\]

_Asw,V. . . área da secção transversal de uma perna do estribo que resiste ao corte na secção considerada

s . . . . . espaçamento da armadura de corte na direção do eixo longitudinal da barra

_asw,V. . . . área da secção transversal da armadura de corte por unidade de comprimento

z . . . . . o braço de alavanca interior. Para uma barra com profundidade constante, correspondente ao momento fletor no elemento em consideração. Na análise de corte do betão armado sem força axial, o valor aproximado z = 0,9d pode ser normalmente utilizado.

_fywd. . . a tensão de cedência de projeto da armadura de corte

θ . . . . . o ângulo entre a escora de compressão do betão e o eixo da barra perpendicular à força de corte

α . . . . . o ângulo entre a armadura de cisalhamento e o eixo da barra perpendicular à força de cisalhamento

β . . . . . inclinação da perna do estribo em relação à resultante da força de corte aplicada

A força de corte é redistribuída uniformemente entre as armaduras individuais que resistem à força de corte com base no ângulo da armadura e na rigidez axial das pernas individuais do estribo.

\[{{V}_{ed}}={{V}_{ed,1}}+{{V}_{ed,2}}+...+{{V}_{ed,n}}\]

\[{{V}_{ed}}={{\varepsilon }_{sw,V}}\cdot z\cdot \sum\limits_{i=1}^{{{n}_{V}}}{{{a}_{sw,i,V}}\cdot {{E}_{sw,i,V}}\cdot \left( \cot \theta +\cot {{\alpha }_{i}} \right)\cdot {{\cos }^{2}}{{\beta }_{i}}}\]

Além disso, a deformação média da armadura considerada na direção da força de corte resultante pode ser derivada:

\[{{\varepsilon }_{sw,V}}=\frac{{{V}_{ed}}}{z\cdot \sum\limits_{i=1}^{{{n}_{V}}}{{{a}_{sw,i,V}}\cdot {{E}_{sw,i,V}}\cdot \left( \cot \theta +\cot {{\alpha }_{i}} \right)\cdot {{\cos }^{2}}{{\beta }_{i}}}}\]

A deformação efectiva da i-ésima armadura pode ser calculada como:

\[{{\varepsilon }_{sw,i,V}}=\frac{{{\varepsilon }_{sw,V}}}{\sin {{\alpha }_{i}}}\cdot \cos {{\beta }_{i}}\]

A tensão numa determinada perna da armadura:

\[{{\sigma }_{sw,i,V}}={{\varepsilon }_{sw,i,V}}\cdot {{E}_{si,V}}\]

Determinação da força num estribo individual devido à torção

A resistência à torção de uma secção pode ser calculada com base numa secção fechada de parede fina, na qual o equilíbrio é satisfeito por um fluxo de corte fechado. As secções sólidas podem ser modeladas por secções de parede fina equivalentes. Para secções não sólidas, a espessura da parede equivalente não deve exceder a espessura real da parede.

O fluxo de cisalhamento nas paredes de uma secção fechada de parede fina devido à torção pode ser calculado como:

\[{{\tau }_{t}}\cdot {{t}_{ef}}=\frac{{{T}_{ed}}}{2{{A}_{k}}}\]

A força de corte numa determinada parede é então:

\[{{V}_{i}}={{\tau }_{t}}\cdot {{t}_{ef}}\cdot {{l}_{i}}\]

_li. . . . comprimento da linha de centro do muro em consideração

Força de corte na alma - o comprimento da linha central da alma pode ser substituído pelo valor do braço de alavanca "z".

\[{{V}_{ed,T}}=\frac{{{T}_{ed}}}{2{{A}_{k}}}\cdot z\]

Força nos estribos que resiste à torção por um metro de comprimento da barra (por unidade de comprimento):

\[{{F}_{sw,T}}=\frac{{{V}_{ed,T}}}{z\cdot \cot \theta }=\frac{{{T}_{ed}}}{2{{A}_{k}}}\cdot tg\theta\]

Decomposições de forças para estribos individuais

Se for definido o mesmo material para todos os estribos, a tensão resultante devido à torção em cada perna do estribo é constante. Então:

\[{{\sigma }_{sw,T}}=\frac{{{F}_{sw,T}}}{{{a}_{sw,T}}}\]

em que_asw,T é a área total dos estribos que resistem à torção por unidade de comprimento.

No caso de os estribos individuais terem materiais diferentes, a rigidez axial das barras individuais deve ser tida em conta.

\[{{F}_{sw,T}}={{F}_{s1,T}}+{{F}_{s2,T}}+{{F}_{s3,T}}+...+{{F}_{sn,T}}=\sum\limits_{i=1}^{{{n}_{T}}}{{{F}_{si,T}}}\]

\[{{\varepsilon }_{sw,T}}=\frac{{{F}_{sw,T}}}{\sum\limits_{i=1}^{{{n}_{T}}}{\left( {{a}_{si,T}}\cdot {{E}_{si,T}} \right)}}\]

_nT. . . . . número de pernas de armadura (grupos de armadura) que resistem à torção

Fsi_,T. . . força no i-ésimo grupo de armadura resultante da torção por unidade de comprimento

_asi,T. . . área da secção transversal da armadura de corte que resiste à torção por unidade de comprimento

_Esi,T. . . módulo de elasticidade de Young do i-ésimo grupo de armaduras resistentes à torção

εsw_,T. . deformação na armadura devido à torção

A tensão resultante em cada estribo devido à torção aplicada é calculada como:

\[{{\sigma }_{sw,i,T}}={{\varepsilon }_{sw,T}}\cdot {{E}_{si,T}}\]

Interação V+T

O cálculo das tensões nos estribos devido ao corte e à torção é então uma soma das tensões devidas a componentes de carga individuais.

\[{{\sigma }_{sw,i}}={{{\sigma }_{sw,i,V}}+{{\sigma }_{sw,i,T}}\]

Força resultante na i-ésima armadura:

\[{{F}_{sw,i}}={{{a}_{sw,i}}\cdot {{\sigma }_{sw,i}}\]

Interação de corte, torção e flexão para armadura longitudinal

Determinação da força em cada armadura longitudinal devido à força normal e ao momento fletor

A aplicação RCS é utilizada para calcular a resposta da secção transversal devido à combinação da força normal e do momento fletor para determinar a tensão e a deformação nos varões longitudinais individuais e na armadura de pré-esforço.

Determinação da força na armadura longitudinal individual devido à força de corte

O incremento da força de tração na armadura longitudinal _ΔFtd a partir da força de corte depende da geometria do modelo de escora e tirante.

\[\ Delta {{F}_{td}}={{{V}_{ed}}}\left( \cot \theta -\cot \alpha \right)\]

_ΔFtd. . . incremento da força de tração na armadura longitudinal devido à força de corte

_Ved. . . . valor de projeto da força de corte que actua na secção em consideração

θ . . . . . o ângulo entre a escora de compressão de betão e o eixo da barra

α . . . . . o ângulo entre a armadura de corte e o eixo da barra

Para a armadura longitudinal situada na corda de tração, a força resultante _Ft na armadura longitudinal devido à combinação N+M+V não deve ser superior a_MEd,max/z(onde_MEd,max é o momento máximo ao longo da viga)

\[{{F}_{t}}=\frac{{{M}_{Ed}}}{z}+0,5{{V}_{ed}}\left( \cot \theta -\cot \alpha \right)\le \frac{{{M}_{Ed,\max }}}{z}\]

A força _ΔFtd é transmitida por todos os tendões de pré-esforço ligados e armaduras localizadas na parte da secção que resiste ao corte (a alma no caso de um perfil em I). Por segurança, a contribuição da armadura de pré-esforço pode ser considerada 0. O pressuposto do cálculo é que o incremento da deformação axial da armadura longitudinal individual que resiste ao corte é constante (Δεs1_,V = Δεs2_,V = .... =Δεp1_,V = Δεp2_,V = ... = _ΔεV = const.). A derivação é válida para um diagrama de trabalho de armadura bilinear com um ramo plástico horizontal. No caso de um diagrama com um ramo inclinado, o cálculo deve ser modificado.

\[\Delta {{F}_{td}}=\Delta {{F}_{s}}+\Delta {{F}_{s}}\]

\[\Delta {{F}_{td}}=\Delta {{\varepsilon }_{V}}\cdot \sum\limits_{i=1}^{{{n}_{s,V}}}{{{A}_{sl,i,V}}\cdot {{E}_{sl,i,V}}}+\Delta {{\varepsilon }_{V}}\cdot \sum\limits_{i=1}^{{{n}_{p,V}}}{{{A}_{pl,i,V}}\cdot {{E}_{pl,i,V}}}\]

_ΔεV. . . . incremento de deformação na armadura longitudinal devido à força de corte

ns_,V. . . . número de armaduras longitudinais que resistem à força de corte

_Asl,i,V. . . . área da i-ésima armadura longitudinal que resiste à força de corte

_Esl,i,V. . . . módulo de elasticidade de Young da i-ésima armadura longitudinal que resiste à força de corte

np_,V. . . . número de tendões que resistem à força de corte

_Apl,i,V. . . . área do i-ésimo tendão que resiste à força de corte

Epl_,i,V. . . . módulo de elasticidade de Young do i-ésimo tendão que resiste à força de corte

Após determinar o valor da força _ΔFtd, a deformação média da armadura _ΔεV pode então ser calculada.

\[\Delta {{\varepsilon }_{V}}=\frac{\Delta {{F}_{td}}}{\sum\limits_{i=1}^{{{n}_{s,V}}}{{{A}_{sl,i,V}}\cdot {{E}_{sl,i,V}}}+\sum\limits_{i=1}^{{{n}_{p,V}}}{{{A}_{pl,i,V}}\cdot {{E}_{pl,i,V}}}}\]

Incremento de tensão nas barras longitudinais individuais devido à força de corte aplicada:

para vergalhões \[\Delta {{\sigma }_{sl,i,V}}=\Delta {{\varepsilon }_{V}}\cdot {{E}_{sl,i,V}}\]

para o tendão \[\Delta {{\sigma }_{pl,i,V}}=\Delta {{\varepsilon }_{V}}\cdot {{E}_{pl,i,V}}\]

Determinação da força em cada armadura longitudinal a partir da torção

É muito importante determinar a armadura longitudinal que resiste à torção. Estas são as armaduras que estão localizadas numa secção de parede fina eficaz alternativa resistente à torção.

\[\frac{\sum{{{A}_{sl}}{{f}_{yd}}}}{{{u}_{k}}}=\frac{{{T}_{ed}}}{2{{A}_{k}}}\cot \theta \]

De acordo com a norma EN 1992-1-1, devem ser cumpridas várias condições para uma armadura longitudinal resistente à torção:

- a armadura deve estar uniformemente distribuída ao longo do comprimento _zi, mas em secções transversais pequenas a armadura pode estar concentrada nos cantos do estribo

- a distância axial máxima da armadura longitudinal é de 350 mm

A contribuição da armadura de pré-esforço não é considerada de acordo com a norma EN 1992-1-1.

A norma EN 1992-2 estabelece que a contribuição da armadura de pré-esforço pode ser considerada, mas o incremento máximo de tensão na armadura de pré-esforço não deve exceder _Δσp ≤ 500MPa. Nesse caso, a fórmula pode ser modificada:

\[\frac{\sum{{{A}_{sl}}{{f}_{yd}}+\sum{{{A}_{p}}\Delta {{\sigma }_{p}}}}}{{{u}_{k}}}=\frac{{{T}_{ed}}}{2{{A}_{k}}}\cot \theta\]

No entanto, uma vez que o incremento da armadura de pré-esforço pode ser considerado, mas fica à escolha do utilizador. Atualmente, a armadura de pré-esforço não é considerada no cálculo.

O pressuposto do cálculo é que o aumento da deformação axial de cada armadura longitudinal resistente ao corte é constante (Δεs1_,T = Δεs2_,T = .... =Δεp1_,T = Δεp2_,T = ... = _ΔεT = const.). A derivação é válida para um diagrama de trabalho de armadura bilinear com um ramo plástico horizontal. No caso de um diagrama com um ramo crescente, o cálculo deve ser modificado.

\[\frac{\sum\limits_{i=1}^{{{n}_{T}}}{{{A}_{sl,i,T}}\cdot \Delta {{\sigma }_{s,i,T}}}}{{{u}_{k}}}=\frac{{{T}_{ed}}}{2{{A}_{k}}}\cot \theta\]

\[\frac{\sum\limits_{i=1}^{{{n}_{T}}}{{{A}_{sl,i,T}}\cdot \Delta {{\varepsilon }_{T}}\cdot {{E}_{s,i,T}}}}{{{u}_{k}}}=\frac{{{T}_{ed}}}{2{{A}_{k}}}\cot \theta\]

\[\Delta {{\varepsilon }_{T}}=\frac{{{T}_{ed}}\cdot {{u}_{k}}}}{2{{A}_{k}}\cdot \sum\limits_{i=1}^{{n}_{T}}}{{{A}_{sl,i,T}}\cdot {{E}_{s,i,T}}}}\cot \theta\]

\[\frac{\sum\limits_{i=1}^{{{n}_{T}}}{{{A}_{sl,i,T}}\cdot \Delta {{\sigma }_{s,i,T}}}}{{{u}_{k}}}=\frac{{{T}_{ed}}}{2{{A}_{k}}}\cot \theta\]

\[\frac{\sum\limits_{i=1}^{{{n}_{T}}}{{{A}_{sl,i,T}}\cdot \Delta {{\varepsilon }_{T}}\cdot {{E}_{s,i,T}}}}{{{u}_{k}}}=\frac{{{T}_{ed}}}{2{{A}_{k}}}\cot \theta\]

\[\Delta {{\varepsilon }_{T}}=\frac{{{T}_{ed}}\cdot {{u}_{k}}}}{2{{A}_{k}}\cdot \sum\limits_{i=1}^{{n}_{T}}}{{{A}_{sl,i,T}}\cdot {{E}_{s,i,T}}}}\cot \theta\]

_Ted. . . . o valor de projeto do binário aplicado na secção em consideração

θ . . . . . inclinação das diagonais de compressão em relação ao eixo longitudinal da viga (idêntica à da força de corte)

_uk. . . . . perímetro da área_Ak

_Af. . . . a área definida pela linha de centro da secção oca de substituição de paredes finas

ns_,T. . . . número de armaduras longitudinais de betão que resistem ao binário

_Asl,i,T. . . área da i-ésima armadura longitudinal de betão resistente ao binário

_ΔεT. . . a alteração da transformação da armadura longitudinal de betão devido ao binário

Δσs_,i,T. . alteração da tensão na i-ésima armadura longitudinal devido ao binário

_Esl,i,T. . . módulo de elasticidade da i-ésima armadura longitudinal de betão que resiste ao binário

Incremento de tensão em cada armadura longitudinal devido ao binário aplicado:

\[\Delta {{\sigma }_{sl,i,T}}=\Delta {{\varepsilon }_{T}}\cdot {{E}_{sl,i,T}}\]

Controlo da limitação do stress

A verificação baseia-se em hipóteses gerais, em que são resolvidos dois estados da secção transversal: a secção não fendilhada (a resistência à tração do betão não é ignorada) e a secção totalmente fendilhada (a resistência à tração do betão é ignorada).A solução com a resistência à tração do betão ignorada é considerada sob os pressupostos do Artigo 7.1 (2) EN 1992-1-1.

Ao calcular a tensão e as deformações, considera-se uma secção não fendilhada, se a tensão de tração na flexão não exceder fct_{, eff}.O valor de fct_{, eff} pode ser considerado como _fctm ou fctm_,fl. O valor de_fctm é utilizado para calcular a largura da fenda e o reforço de tração.

Como parte desta verificação, lidamos com quatro casos básicos em termos de limite de tensão.

• 7.2 (2) A tensão de compressão em barras expostas a ambientes das classes de exposição XD, XF e XS deve ser limitada:

\[\left| {{s}_{c}} \right|\le {{k}_{1}}{{{f}_{ck}}\]

\[{{k}_{1}}=0,6\]

• 7.2 (3) A tensão no betão sob as cargas quase permanentes é limitada:

\[\left| {{s}_{c}} \right|\le {{k}_{2}}{{{f}_{ck}}\]

\[{{k}_{2}}=0,45\]

• 7.2 (5) As tensões de tração na armadura sob a combinação caraterística de cargas devem ser limitadas:

\[\left| {{s}_{s}} \right|\le {{k}_{3}}{{{f}_{yk}}\]

\[{{k}_{3}}=0,8\]

• 7.2 (5) Quando a tensão é causada por uma deformação imposta, a tensão de tração não deve exceder:

\[\left| {{s}_{s}} \right|\le {{k}_{4}}{{f}_{yk}}\]

\[{{k}_{4}}=1\]

Os valores _k1, _k2, _k3, _k4 para utilização num país podem ser consultados no respetivo anexo nacional. Os valores recomendados são 0,8; 1 e 0,75, respetivamente, tensão de cedência caraterística da armadura, _fck resistência cilíndrica caraterística _fck determinada aos 28 dias.

Fissuras

A formação de fissuras

Uma caraterística das estruturas de betão armado sujeitas a tensões de flexão ou de tração é a ocorrência de fissuras nos pontos em que a tensão de tração no betão excede a resistência à tração do betão. Para a durabilidade da estrutura e também para a estética da estrutura, é importante assegurar que as fissuras resultantes sejam tão pequenas quanto possível. O cálculo das larguras das fissuras, bem como as larguras máximas permitidas para as diferentes classes de exposição, são apresentados na norma EN 1992-1-1, capítulo 7.3.

No primeiro passo do cálculo, determina-se se a secção transversal está fendilhada ou não. A largura da fenda em si é sempre calculada a partir da combinação de cargas quase permanentes ou frequentes (dependendo do anexo nacional), mas a formação de fendas tem de ser verificada a partir de todas as combinações SLS especificadas. Assim, podem ocorrer dois casos:

• A tensão máxima de tração nas fibras de betão não excederá a resistência à tração do betão a partir de qualquer combinação de cargas (_ME,qp quase permanente,_ME,fr frequente ou_ME,k caraterístico), pelo que se considera a secção transversal sem fissuras.

\[{{M}_{E,i}}\le {{M}_{cr}}={{f}_{ct,ef}}\frac{{I}_{I}}{h-{{a}_{I}}}\]

• Se as fendas se desenvolverem para qualquer uma das combinações (quase permanente, frequente ou caraterística), ou seja, o momento fletor desenvolvido a partir da combinação de cargas considerada é maior do que o momento crítico_Mcr, a secção está fendilhada a partir dessa combinação de cargas e as caraterísticas da secção fendilhada e a largura da fenda têm de ser calculadas.

\[{{M}_{E,i}}>{{M}_{cr}}={{f}_{ct,ef}}\frac{{I}_{I}}{h-{{a}_{I}}}\]

_ME,i. . o momento fletor obtido a partir de um pente de carga SLS. Assim, pode ser_ME,qp,_ME,fr ou_ME,k.

fct_,ef . . a resistência à tração do betão no momento considerado. Se o betão tiver mais de 28 dias, considera-se uma resistência igual a _fctm.

Cálculo da largura da fenda

Num elemento carregado por flexão, a formação de fendas divide-se em 2 fenómenos:

• Fase de formação de fissuras (etapa número 2 da Fig. 1)
• Desenvolvimento de fissuras estabilizadas (fase número 3 na Fig. 1)

\[ \textsf{\textit{\footnotesize{Fig. 1 Fases do comportamento da secção de betão armado durante o carregamento}}}\]

Fase de desenvolvimento da fissura

Esta é a parte inicial do processo quando as fendas individuais ainda estão a aparecer gradualmente até que toda a parte de tração da barra seja afetada por fendas que estão aproximadamente igualmente distribuídas ao longo do comprimento da barra. A primeira fissura é formada quando a força na tira tensionada excede o valor da força crítica_Nr (Força crítica de tração, ver abaixo), e outras fissuras desenvolvem-se até um nível de carga que exerce uma força na tira tensionada igual a aproximadamente 1,_3Ncr (fase número 2 na Fig. 1).

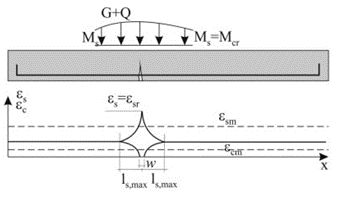
\[ \textsf{\textit{\footnotesize{Fig. 2 Tensões do betão e da armadura no momento da primeira fissura}}}\]

As fissuras em desenvolvimento dividem-se em 2 tipos - fissuras primárias e secundárias. As fissuras primárias ocorrem nas fibras de tração quando a resistência efectiva à tração do betão (fct_,eff) é atingida. As fissuras primárias representam o primeiro padrão de fissuras (Fig. 2). Entre as fissuras primárias formam-se depois fissuras secundárias mais curtas (Fig. 3). A tensões correspondentes a cerca de 1,2 a 1,5 _σsr (geralmente considera-se um valor médio de 1,3 _σsr, onde _σsr é a tensão na armadura na formação de fissuras primárias na zona de tração do betão), o desenvolvimento de fissuras secundárias também está concluído.

\[ \textsf{\textit{\footnotesize{Fig. 3 Fissuras primárias e secundárias}}\]

A largura da fenda na fase de formação da fenda pode ser calculada da seguinte forma:

\[{{w}_{k}}=2{{l}_{s,\max }}\left( {{\varepsilon }_{sm}}-{{\varepsilon }_{cm}} \right)\]

\[ \textsf{\textit{\footnotesize{Fig. 4 Caraterísticas do comprimento de transmissão para a primeira fissura}}}\]

Fase de fissuração estabilizada

Depois de exceder aproximadamente 1,3 vezes a força crítica na zona de tração, não se formam novas fendas, o número de fendas no elemento é estabilizado e apenas a largura das fendas existentes aumenta com o carregamento adicional (fase número 3 na Fig. 1).

\[ \textsf{\textit{\footnotesize{Fig. 5 Tensões do betão e da armadura na fase de fendilhação estabilizada}}}\]

A largura da fenda durante o desenvolvimento estável pode ser calculada como:

\[{{w}_{k}}={{s}_{r,\max }}\left( {{\varepsilon }_{sm}}-{{\varepsilon }_{cm}} \right)\]

\[ \textsf{\textit{\footnotesize{Fig. 6 Fissuração estabilizada}}}\]

Força de tração crítica

O cálculo é baseado no modelo de corda de tração (TCM). A consideração básica é calcular a capacidade última de uma faixa de betão armado formada por um varão de armadura de área_As,eff rodeado por uma área efectiva de betão de tração_Ac,eff, que é capaz de resistir à tensão de tração até que a resistência à tração fct_,eff seja excedida (normalmente consideramos _fctm). Assumindo uma ligação perfeita entre a armadura e o betão, podemos considerar que até à ocorrência da primeira fissura, a remodelação da armadura e do betão envolvente é idêntica. Assim, a força máxima na faixa de tração imediatamente antes da primeira fissura_Nr pode ser determinada:

\[{{N}_{r}}={{A}_{c,eff}}\cdot {{f}_{ctm}}+{{A}_{s,eff}}\cdot {{\sigma }_{s}}\]

Introduzindo a substituição

\[{{\alpha }_{e}}={}^{{{E}_{s}}}/{}_{{{E}_{cm}}};{{\rho }_{p,eff}}={}^{{{A}_{s,eff}}}/{}_{{{A}_{c,eff}}}\]

obtemos:

\[{{N}_{r}}={{A}_{c,eff}}\cdot {{f}_{ctm}}\cdot \left( 1+{{\alpha }_{e}}\cdot {{\rho }_{p,eff}} \right)\]

Logo após a formação da primeira fenda, toda a força_Nr é transferida pela armadura e, portanto, a tensão na armadura que passa pela fenda recém-formada pode ser calculada como:

\[{{\sigma }_{sr}}=\frac{{{f}_{ctm}}}{{{\rho }_{p,eff}}}}\cdot \left( 1+{{\alpha }_{e}}\cdot {{\rho }_{p,eff}} \right)\Rightarrow {{\varepsilon }_{sr}}=\frac{{{f}_{ctm}}}{{{E}_{s}}\cdot {{\rho }_{p,eff}}}\cdot \left( 1+{{\alpha }_{e}}\cdot {{\rho }_{p,eff}} \right)\]

Cálculo da largura da fenda de acordo com EC 1992-1-1

A seguinte equação é utilizada para calcular a largura das fendas em elementos de betão armado:

\[{{w}_{k}}={{s}_{r,\max }}\left( {{\varepsilon }_{sm}}-{{\varepsilon }_{cm}} \right)\]

_sr,max. . . espaçamento máximo entre fissuras

_εsm . . . . a deformação média da armadura a partir da combinação de cargas, incluindo os efeitos da rigidez à tração.

_εcm . . . . deformação média do betão entre fissuras

Cálculo da diferença de deformação

A diferença de deformação da armadura e do betão entre fissuras pode ser obtida a partir da equação:

\[{{\varepsilon }_{sm}}-{{\varepsilon }_{cm}}=\frac{{{\sigma }_{s}}-{{k}_{t}}\cdot \frac{{{f}_{ct,eff}}}}{{{\rho }_{p,eff}}\cdot \left( 1+{{\alpha }_{e}}\cdot {{\rho }_{p,eff}} \right)\,}{{{E}_{s}}}\ge 0,6\frac{{{\sigma }_{s}}}{{{E}_{s}}}\]

σs_. . . . a tensão na armadura na fenda a partir da combinação de cargas em consideração

_{kt .} . . . um coeficiente empírico que tem em conta a deformação média, dependente da duração da carga. Pode assumir valores de 0,6 para análises a curto prazo. Para a análise a longo prazo, a redução da rigidez do compósito para cerca de 70% é tida em conta, pelo que o seu valor é 0,4, que inclui a taxa de degradação da coesão entre a armadura e o betão devido ao tempo.

_αe. . . . o rácio efetivo dos módulos elásticos

\[{{\alpha }_{e}}={}^{{{E}_{s}}}/{}_{{{E}_{cm}}}\]

_ςp,eff. . . . nível efetivo de reforço

\[{{\rho }_{p,eff}}={}^{\left( {{A}_{s,eff}}+{{\xi }^{2}_{1}}A_{p}^{\acute{\ }} \right)}/{}_{{{A}_{c,eff}}}\]

_Ac,eff. . . . a área efectiva do betão sob tração que envolve a armadura (determinação de_Ac,eff abaixo)

_As,eff. . . . a área da armadura ligada localizada na área de_Ac,eff

_Ap' . . . . é a área dos tendões pré ou pós-tensionados dentro de_Ac,eff

_ξ1. . . . . é o rácio ajustado da resistência da ligação, tendo em conta os diferentes diâmetros do aço de pré-esforço e de reforço:

\[{{\xi }_{1}}=\sqrt{\xi \,\cdot \,\frac{{{\phi }_{s}}}{{{\phi }_{p}}}}\]

ξ . . . o rácio da resistência da ligação entre o aço de pré-esforço e o aço de reforço (Quadro 6.2)

_ϕs. . . maior diâmetro da barra de aço de reforço

_ϕp. . . o diâmetro ou diâmetro equivalente do aço de pré-esforço

Para feixes,_Ap é a área da armadura no tendão

\[{{\phi }_{p}}=1,6\sqrt{{{A}_{p}}}\]

Para fios simples de sete fios, em que _φfio é o diâmetro do fio

\[{{\phi }_{p}}=1,75\,\,{{\phi }_{wire}}\]

Para cordões simples de três fios em que _φfio é o diâmetro do fio

\[{{\phi }_{p}}=1,20\,\,{{\phi }_{wire}}\]

Se apenas a armadura de pré-esforço for utilizada para evitar a fendilhação, então deve ser considerado o seguinte.

\[{{\xi }_{1}}=\sqrt{\xi \,}\]

Em elementos pré-esforçados, não é necessária uma área mínima de armadura ligada, desde que, sob a combinação caraterística de carga e o valor caraterístico da força de pré-esforço, a tensão de tração em qualquer fibra não seja superior à resistência à tração do betão, fct_,eff. (ver EN 1992-1-1 cap. 7.3.2 para mais pormenores)

A área efectiva do betão em tração

Um passo importante mas simultaneamente o mais complicado do cálculo é a determinação da área efectiva do betão à tração que envolve a armadura. Tanto o Eurocódigo como o Código Modelo consideram modos simples de carregamento, onde o elemento de betão armado é carregado por flexão uniaxial ou tensão. O valor da altura efectiva é determinado como:

\[{{h}_{c,eff}}=\min \left\{ 2,5\left( h-d \right);\frac{\left( h-x \right)}{3};{}^{h}/{}_{2} \right\}\]

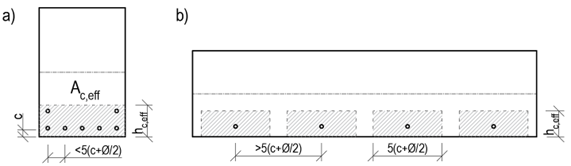
\[ \textsf{\textit{\footnotesize{Fig. 6 Determinação de Ac,eff para barras fletidas (esquerda) e barras em tração (direita)}}}\]

Normalmente, o valor hc_,eff = 2,5 (h-d) é crítico. Para elementos tensionados, o limite superior é h/2, enquanto para elementos dobrados é (h-x)/3. No entanto, a área_Ac,eff também é limitada pela largura determinada a partir da equação 5(c+ϕ/2). Se o espaçamento das armaduras for superior a 5(c+ϕ/2), então a área efetiva do betão tensionado de largura 5(c+ϕ/2) é considerada para as barras individuais.

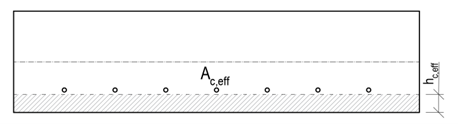
\[ \textsf{\textit{\footnotesize{Fig. 9 Determinação de Ac,eff com base no espaçamento da armadura}}\]

Distância máxima de fendilhação

Ao calcular a distância máxima de fendilhação_sr,max, podem ocorrer dois casos:

• A distância axial da armadura ligada não excede uma distância de 5(c+ϕ/2) - Fig. 9a
• A distância axial das armaduras ligadas é superior a 5(c+ϕ/2) - Fig. 9b

O cálculo da distância máxima de fendilhação_sr,max para o caso de as distâncias axiais das armaduras não excederem o valor 5(c+ϕ/2) é definido da seguinte forma:

\[{{s}_{r,\max }}={{{k}_{3}}c+{{{k}_{1}}{{k}_{2}}{{{k}_{4}}\frac{\phi }{{{\rho }_{p,eff}}}\]

c . _. . . . valor do recobrimento do betão em mm. Uma vez que o valor do recobrimento pode ser diferente para a armadura de borda para as bordas horizontais e verticais, recomenda-se considerar o valor máximo de recobrimento encontrado para a armadura em consideração.

_ϕ . . . . diâmetro da armadura ligada. No caso de diâmetros de armadura diferentes, o diâmetro equivalente deve ser calculado de acordo com a Equação 7.12 da EN 1992-1-1.

\[{{\phi }_{eq}}=\frac{{{n}_{1}}\phi _{1}^{2}+{{n}_{2}}\phi _{2}^{2}}{{{n}_{1}}{{\phi }_{1}}+{{n}_{2}}{{\phi }_{2}}\]

_k1. . . . é um coeficiente que tem em conta as propriedades de ligação da armadura ligada

• _k1 = 0,8 para varões de alta aderência
• _k1 = 1,6 para varões com uma superfície efetivamente plana (por exemplo, tendões de pré-esforço)

_k2. . . . é um coeficiente que tem em conta a distribuição das deformações

• _k2 = 1,0 para a flexão
• _k2 = 0,5 para a tração pura

Para casos de tensão excêntrica ou para áreas locais, devem ser utilizados valores intermédios de _k2 que podem ser calculados a partir da relação:

\[{{k}_{2}}=\frac{{{\varepsilon }_{1}}+{{\varepsilon }_{2}}}{2{{\varepsilon }_{1}}}\]

k3_. . . . coeficiente que expressa o comprimento da área próxima de uma fissura onde a ligação entre o betão e a armadura é quebrada. O valor recomendado do CE de base _k3 = 3,4 pode ser modificado pelo Anexo Nacional.

O coeficiente k4_. . . . exprime a relação entre a ligação e a resistência à tração do betão. O valor recomendado do CE de base k4 = 0,425 pode ser ajustado pelo Anexo Nacional.

O cálculo da distância máxima de fendilhação_sr,max para o caso de as distâncias axiais das armaduras excederem o valor 5(c+ϕ/2) é definido da seguinte forma:

\[{{s}_{r,\max }}=1,3\left( h-x \right)\]

Valores máximos de distância de fenda de acordo com a equação

\[{{s}_{r,\max }}=1,3\left( h-x \right)\]

devem ser sempre superiores aos valores determinados pela equação

\[{{s}_{r,\max }}={{k}_{3}}c+{{k}_{1}}{{k}_{2}}{{k}_{4}}}{\phi }/{{{\rho }_{p,eff}}}\;\]

caso contrário, recomenda-se que se considere a maior distância obtida a partir das equações acima. A equação para a deformação no betão/reforço não é modificada para o caso da grande distância axial do reforço. Em áreas com larguras de fendas controladas, a distância axial das armaduras individuais não deve ser superior a 5(c+ϕ/2).

Cálculo da largura da fenda implementado no RCS

Determinação da área efectiva_Ac,eff

Uma vez que não é tão simples determinar qual a armadura que pode ser considerada como armadura longitudinal resistente à fendilhação,_Ac,eff é determinada utilizando o seguinte processo iterativo.

• De todas as armaduras que actuam em tração, é determinado o centro de força de tração Cg_,s,1. A profundidade efectiva da armadura d é a distância entre Cg_,s, e a fibra de betão mais comprimida calculada na direção do momento fletor resultante. Ao mesmo tempo, são determinadas a posição do eixo neutro e a altura da área comprimida x para a secção fendilhada. Isto torna possível determinar a altura efectiva hc_,eff:

\[{{h}_{c,eff}}=\min \left\{ 2,5\left( h-d \right);\frac{\left( h-x \right)}{3};{}^{h}/{}_{2} \right\}\]

• Ao excluir todas as armaduras que se encontram fora de_Ac,eff,1, o novo centro da armadura Cg_,s,2 é determinado, juntamente com a nova profundidade efectiva da armadura d, a altura efectiva hc_,eff é determinada da mesma forma que no passo anterior, apenas com valores de entrada alterados.

Mais uma vez, é verificado se toda a armadura tensionada em consideração se encontra no_Ac,eff,2. Se esta condição for satisfeita, a iteração pode ser terminada e os valores de hc_,eff,2,_Ac,eff,2 e_As,eff,2 são apresentados como os valores resultantes no IDEA StatiCa RCS.

Casos possíveis de cálculo da largura da fenda

Em geral, podem ocorrer três casos no cálculo da largura da fenda:

• A armadura de tração encontra-se na região_Ac,eff, sendo a distância axial das armaduras individuais inferior a 5(c+ϕ/2). Então, as seguintes definições são utilizadas para o cálculo:

\[{{s}_{r,\max }}={{k}_{3}}c+{{{k}_{1}}{{k}_{2}}{{{k}_{4}}\frac{\phi }{{{\rho }_{p,eff}}}\]

\[{{\varepsilon }_{sm}}-{{\varepsilon }_{cm}}=\frac{{{\sigma }_{s}}-{{{k}_{t}}\,\cdot \,\frac{{{f}_{ct,eff}}}}{{{\rho }_{p,eff}}}\,\cdot \,\left( 1+,{{\alpha }_{e}}\cdot \,{{\rho }_{p,eff}} \right)\,\,}{{{E}_{s}}}\ge 0,6\frac{{{\sigma }_{s}}}{{{E}_{s}}}\]

• A armadura de tração encontra-se no_Ac,eff, com a distância axial das armaduras individuais a exceder a distância 5(c+ϕ/2). De seguida, são utilizadas as seguintes definições para o cálculo:

\[{{s}_{r,\max }}=1,3\left( h-x \right)\]

\[{{\varepsilon }_{sm}}-{{{\varepsilon }_{cm}}=\frac{{{\sigma }_{s}}-{{k}_{t}}\,\cdot \,\frac{{{f}_{ct,eff}}}}{{{\rho }_{p,eff}}}\,\cdot \,\left( 1+,{{\alpha }_{e}}\cdot \,{{\rho }_{p,eff}} \right)\,\,}{{{E}_{s}}}\ge 0,6\frac{{{\sigma }_{s}}}{{{E}_{s}}}\]

• A armadura de tração não se encontra no_Ac,eff (isto pode ser causado, por exemplo, por uma cobertura espessa).

Neste caso, não seria possível calcular a largura das fendas. Por isso, o cálculo da altura efectiva hc_,eff é modificado da seguinte forma:

\[{{h}_{c,eff}}=\min \left\{ 2,5\left( h-d \right);h/2 \right\}\]

Ao mesmo tempo, é apresentada a seguinte não conformidade:

A área efectiva de betão à tração que envolve a armadura ou os tendões de pré-esforço de profundidade hc_,eff, em que hc_,eff é o menor de 2,5(h - d) ou h/2. Considerando o valor como(h - x)/3, a armadura está fora da área efectiva do betão em tração, pelo que não seria possível calcular a largura da fenda de acordo com o ponto 7.3.4.

Diagrama N-M-κ

O diagrama N-M-κ mostra a curvatura de um elemento (rigidez à flexão) em função de um momento fletor e de uma força normal aplicados. Existem três tipos de diagramas N-M-κ:
- curto prazo,
- longo prazo
- ULS.
Estes diagramas diferem nos tipos de diagramas tensão-deformação utilizados para o cálculo (explicados abaixo).

O cálculo da rigidez para estados caraterísticos selecionados da secção transversal é utilizado para determinar o diagrama N-M-κ. Em geral, pode ser qualquer estado da secção transversal a partir do qual a resposta é calculada e a partir do qual a rigidez à flexão e a curvatura são derivadas. No IDEA RCS, consideramos quatro pontos caraterísticos (_Mr,_Mc,_Ms e_Mu)

_Mr - o momento de fendilhação

A secção transversal é sujeita a uma força normal definida pelo utilizador e o plano de deformação começa a rodar (na direção do momento fletor especificado) até que a resistência à tração máxima do betão seja atingida numa fibra de betão (para o grau de betão C30/37, isto é _fctm = 2,896 MPa). Para o cálculo, é utilizado um diagrama de tensão-deformação bilinear com um ramo plástico horizontal tanto para a armadura como para o betão.

_Mc - o momento fletor quando a resistência à compressão do betão é atingida

A partir do passo anterior, é identificada a fibra de betão mais utilizada na compressão. Para esta fibra, é definida a deformação na resistência máxima do betão (_fck/Ecm para curto prazo, _fck/Eceff para longo prazo e _fcd/Ecm para o diagrama ULS). Com base na força normal definida e na direção do momento fletor, o processo de iteração para encontrar o plano de deformação é executado para encontrar um equilíbrio entre a resposta da secção transversal e a força normal definida. É utilizado para o cálculo um diagrama tensão-deformação bilinear com um ramo plástico horizontal para a armadura e o betão.

_Ms - o momento fletor quando é atingida a tensão de cedência na barra de armadura mais utilizada

Outro ponto caraterístico do diagrama N-M-κ é o estado de tensão da secção quando a tensão de cedência no varão de armadura mais utilizado é atingida (a deformação do varão é igual a _fyk/Es para os diagramas de curto e longo prazo, _fyd/Es para o diagrama ULS). O processo de iteração encontra um equilíbrio de forças normais na secção transversal rodando o plano de deformação em torno do ponto especificado pela posição do varão de armadura mais utilizado. Para o cálculo, é utilizado um diagrama de tensão-deformação bilinear com um ramo plástico horizontal para a armadura e o betão.

_Mu - o momento fletor no estado limite último

Esta é a capacidade de carga última de uma secção transversal em flexão, quando a secção transversal está sujeita a uma força normal de projeto definida _Ned. Para o cálculo da capacidade da secção transversal, assume-se que a resistência à compressão na fibra mais utilizada do betão e a resistência à tração no varão de armadura mais utilizado são atingidas (deformação máxima para o betão _εcu = 0,1 e para a armadura εs_,max = 0,5. Para o cálculo, é utilizado um diagrama bilinear tensão-deformação com um ramo plástico horizontal para a armadura e um diagrama parábola-retângulo para o betão.

A rigidez e a curvatura resultantes devido à combinação definida pelo utilizador da força normal e do momento fletor ( Md) são então calculadas utilizando a interpolação linear dos pontos caraterísticos individuais do diagrama N-M-κ.

Cálculo de rigidezes e curvaturas

As rigidezes e curvaturas para cada estado de tensão na secção transversal (_Mr,_Mc,_Ms ou_Mu) são calculadas diretamente a partir da rotação do plano de deformação.

\[E{{A}_{x}}=\frac{N}{{{\varepsilon }_{x}}}\]

_EAx. . . rigidez axial do elemento

N . . . . a força normal especificada

_εx. . . deformação axial no centro de gravidade da secção transversal de betão

\[E{{I}_{y}}=\frac{M}{\kappa }\]

_EIy. . . rigidez à flexão do elemento

M . . . o momento fletor calculado_Mr,_Mc,_Ms ou_Mu

κ . . . . a curvatura do elemento, calculada como a tangente do ângulo entre o plano da deformação e o eixo longitudinal do elemento

Exemplo prático

Uma secção transversal de betão (betão de grau C30/37) é reforçada com armadura ϕ32 (grau B500B). A combinação quase-permanente definida é N = -730 kN e_My = 557 kNm.

O plano de deformação para o ponto caraterístico_Ms é determinado pelo IDEA RCS da seguinte forma:

\[E{{A}_{x}}=\frac{N}{{{\varepsilon }_{x}}}=\frac{730}{6,9471\cdot {{10}^{-4}}}=1050,798MN\]

\[\kappa =\frac{28,4386\cdot {{10}^{-4}}}}{0,463}=61,422\cdot {{10}^{-4}}{{{m}^{-1}}\]

\[E{{I}_{y}}=\frac{{{M}_{s}}}{\kappa }=\frac{2277,4}{61,422\cdot {{10}^{-4}}}=370,776MN{{m}^{2}}\]

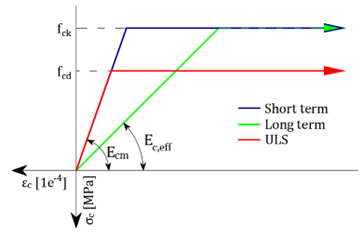
Diagramas de tensão-deformação utilizados para o cálculo

Reforço -_Mr,_Mc,_Ms e_Mu

Betão -_Mr,_Mc,_Ms

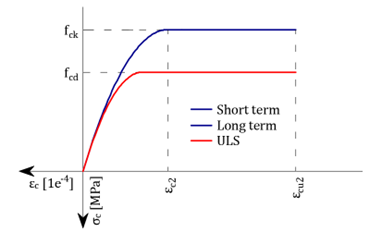
Betão -_Mu

Literatura

[1] Bradáč Betonové konstrukce (estruturas de betão), 1.part: Dimensionamento de elementos de betão armado e simples, EXPERT Ostrava, 1996

[2] ČSN EN 1992-1-1 (73 1201) Eurocódigo 2: Dimensionamento de estruturas de betão - Parte 1-1: Regras gerais e regras para edifícios, inc. alteração NA ed. A (2007) e revisão 1 (2009)

[3] ČSN EN 1992-2 (73 6208) Eurokód 2: Navrhování betonových konstrukcí - Část 2: Betonové mosty - Navrhování a konstrukční zásady

[4] Navrátil, J. Předpjaté betonové konstrukce. 2. vydání, Akademické nakladatelství CERM, Vysoké učení technické v Brně, Fakulta stavební, 2008

[5] Šmiřák, S. Pružnost a plasticita I, Vysoké učení technické v Brně, Akademické nakladatelství CERM, Brno, 1999

[6] Vondráček, R. Métodos numéricos no projeto não linear de betão, Diplomová práce, ČVUT, Praha, 2000

[7] Zich, M. a kolektiv Konstrukční Eurokódy - Příklady posouzení betonových prvků dle Eurokódů, livro em linha http://www.stavebniklub.cz/konstrukcni-eurokody-onbecd/, Verlag Dashöfer, 2010