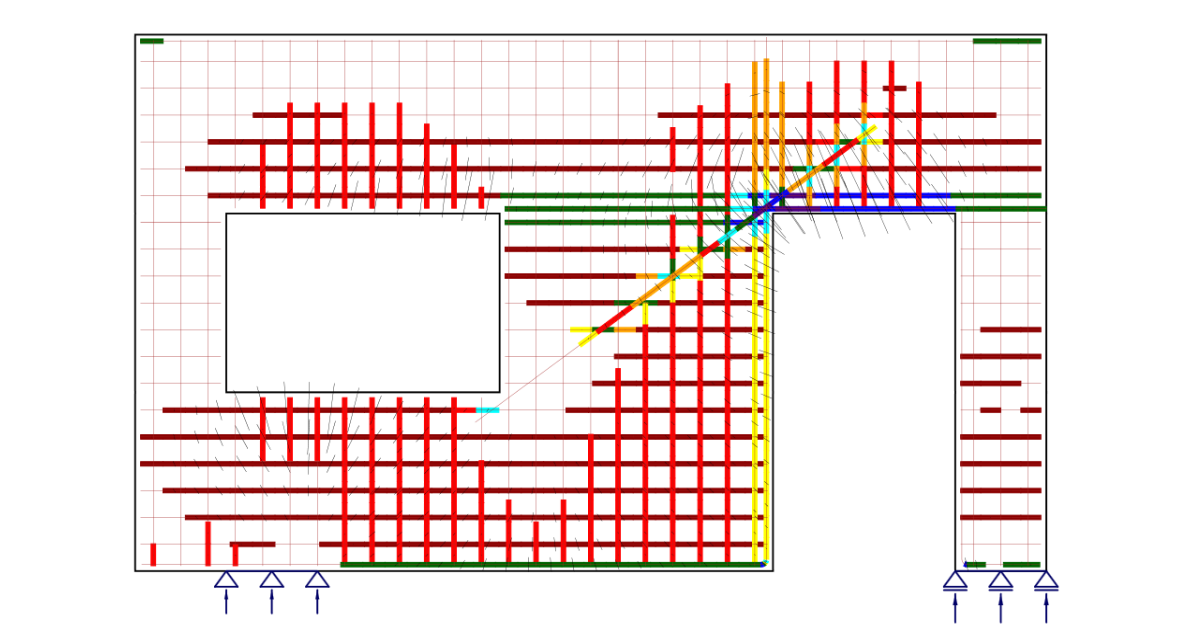
IDEA StatiCa Detail – Structural design of concrete discontinuities
The theoretical background is based on COMPATIBLE STRESS FIELD DESIGN OF STRUCTURAL CONCRETE
(Kaufmann et al., 2020)
Structural design of concrete discontinuities in IDEA StatiCa Detail
Introduction to the CSFM method
General introduction for the structural design of concrete details
Main assumptions and limitations
Design tools for reinforcement
Analysis model of IDEA StatiCa Detail
Introduction to finite element implementation
Supports and load transmitting components
Load transfer at trimmed ends of beams
Geometric modification of cross-sections
Finite element types
Meshing
Solution method and load-control algorithm
Presentation of results
Model verification
Limit states, crack width calculation, and Tension stiffening
Structural verifications according to EUROCODE
- Material models (EN)
- Safety factors
- Ultimate limit state analysis
- Partially loaded areas (PLA)
- Serviceability limit state analysis
Structural verifications according to ACI 318-19
- Material models (ACI)
- Strength reduction and load factors
- Strength verifications
- Bearing and anchorage zones - Partially loaded areas
- Serviceability verifications
Structural verifications according to AS 3600
- Material models (AUS)
- Stress reduction and load factors
- Strength and anchorage verifications
- Serviceability checks
Prestressing in Detail - Model description
Introduction to the CSFM method
Analysis model of IDEA StatiCa Detail
Introdução à implementação de elementos finitos
O CSFM considera campos de tensão contínuos no betão (elementos finitos 2D), complementados por elementos discretos de "barras" que representam a armadura (elementos finitos 1D). Assim, a armadura não é difusamente incorporada nos elementos finitos 2D do betão, mas explicitamente modelada e ligada a eles. No modelo de cálculo é considerado um estado de tensão plano.
\[ \textsf{\textit{\footnotesize{Fig. 6\qquad Visualização do modelo de cálculo de um elemento estrutural (viga aparada) no Idea StatiCa Detail.}}}\]
Podem ser modeladas paredes e vigas inteiras, bem como pormenores (partes) de vigas (região de descontinuidade isolada, também designada por extremidade aparada). No caso de paredes e vigas inteiras, os apoios devem ser definidos de forma a resultar numa estrutura (externamente) isostática (estaticamente determinada) ou hiperestática (estaticamente indeterminada). A transferência de carga nas extremidades cortadas das vigas é introduzida através de uma zona de transferência especial de Saint-Venant, que assegura uma distribuição de tensões realista na região de pormenor analisada.
Tipos de elementos finitos
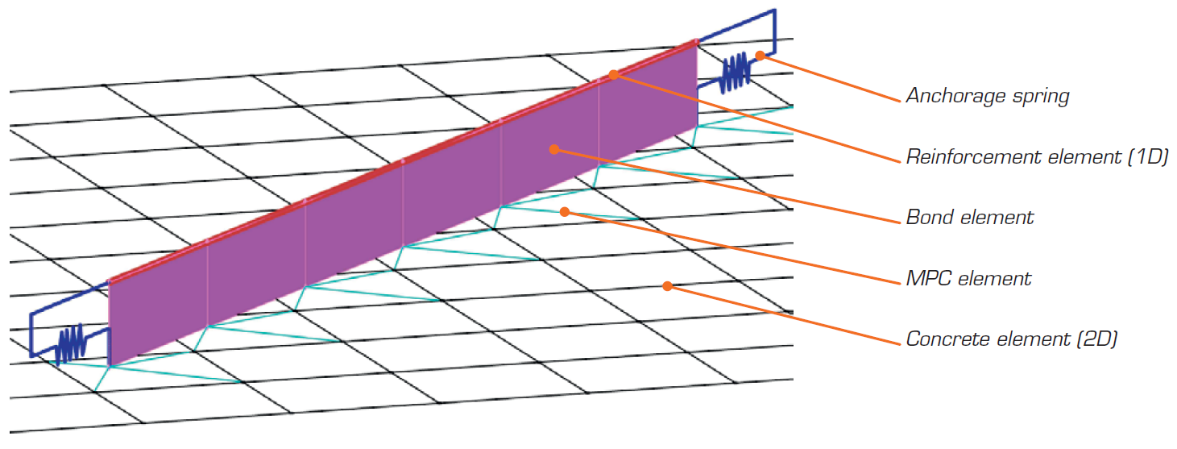
O modelo de análise de elementos finitos não linear (inelástico) é criado por vários tipos de elementos finitos utilizados para modelar o betão, a armadura e a ligação entre eles. Os elementos de betão e de armadura são inicialmente engrenados de forma independente e depois ligados entre si através de restrições multiponto (elementos MPC). Isto permite que a armadura ocupe uma posição arbitrária e relativa em relação ao betão. Se for necessário calcular a verificação do comprimento da ancoragem, são inseridos elementos de ligação e de mola final de ancoragem entre a armadura e os elementos MPC.
\[ \textsf{\textit{\footnotesize{Fig. 13\qquad Modelo de elementos finitos: elementos de reforço mapeados para a malha de betão utilizando elementos MPC e elementos de ligação.}}}\]
Betão
O betão é modelado utilizando elementos de casca quadrilaterais e trilaterais, CQUAD4 e CTRIA3. Estes podem ser definidos por quatro ou três nós, respetivamente. Assume-se que apenas existem tensões planas nestes elementos, ou seja, não são consideradas tensões ou deformações na direção z.
Cada elemento tem quatro ou três pontos de integração que são colocados a aproximadamente 1/4 do seu tamanho. Em cada ponto de integração de cada elemento, são calculadas as direcções das deformações principais α1, α2. Em ambas as direcções, as tensões principais σc1, σc2 e as rigidezes E1, E2 são avaliadas de acordo com o diagrama tensão-deformação do betão especificado, conforme a Fig. 2. Deve notar-se que o impacto do efeito de suavização da compressão associa o comportamento da direção principal de compressão ao estado atual da outra direção principal.
Reforço
As armaduras são modeladas por elementos de barra 1D de dois nós (CROD), que apenas têm rigidez axial. Estes elementos são ligados a elementos especiais de "ligação" que foram desenvolvidos para modelar o comportamento de deslizamento entre um varão de reforço e o betão circundante. Estes elementos de ligação são posteriormente ligados por elementos MPC (multi-point constraint) à malha que representa o betão. Esta abordagem permite a criação de malhas independentes para a armadura e para o betão, enquanto a sua interligação é assegurada posteriormente.
Elementos de ligação
O comprimento de ancoragem é verificado através da implementação das tensões de corte de ligação entre os elementos de betão (2D) e os elementos de barras de reforço (1D) no modelo de elementos finitos. Para este efeito, foi desenvolvido um elemento finito do tipo "ligação".
A definição do elemento de ligação é semelhante à de um elemento de casca (CQUAD4). Também é definido por 4 nós, mas, ao contrário de uma casca, apenas tem uma rigidez ao corte diferente de zero entre os dois nós superiores e os dois inferiores. No modelo, os nós superiores estão ligados aos elementos que representam as armaduras e os nós inferiores aos que representam o betão. O comportamento deste elemento é descrito pela tensão de ligação, τb, como uma função bilinear do deslizamento entre os nós superiores e inferiores, δu, ver Fig. 14.
\[ \textsf{\textit{\footnotesize{Fig. 14\qquad (a) ilustração concetual da deformação de um elemento de ligação; (b) uma função tensão-deformação.}}}\]
O módulo de rigidez elástica da relação ligação-deslizamento, Gb, é definido da seguinte forma:
\[G_b = k_g \cdot \frac{E_c}{Ø}\]
onde:
coeficientekg dependente da superfície do varão de reforço (por defeitokg = 0,2)
Ec módulo de elasticidade do betão (tomado como Ecm no caso da EN)
Ø o diâmetro do varão de reforço
Os valores de cálculo (valores ponderados) da tensão última de corte da ligação, fbd, fornecidos nos respectivos códigos de cálculo selecionados EN 1992-1-1 ou ACI 318-19 são utilizados para verificar o comprimento da ancoragem. O endurecimento do ramo plástico é calculado por defeito como Gb/105.
Mola de ancoragem
O fornecimento de extremidades de ancoragem aos varões de reforço (i.e., curvas, ganchos, laços...), que cumprem as prescrições dos códigos de dimensionamento, permite a redução do comprimento de ancoragem básico dos varões(lb,net) por um determinado fator β (referido como o "coeficiente de ancoragem" abaixo). O valor de projeto do comprimento de ancoragem(lb) é então calculado da seguinte forma:
\[l_b = \left(1 - \beta\right)l_{b,net}\]
A redução pretendida em lb,net é equivalente à ativação do varão de armadura na sua extremidade a uma percentagem da sua capacidade máxima dada pelo coeficiente de redução da ancoragem, como se mostra na Fig. 15a.
\[ \textsf{\textit{\footnotesize{Fig. 15\qquad Modelo para a redução do comprimento da ancoragem:}}}\]
\[ \textsf{\textit{\footnotesize{(a) força de ancoragem ao longo do comprimento de ancoragem do varão de reforço; (b) relação constitutiva da força de ancoragem-deslizamento.}}}\]
A redução do comprimento de ancoragem é incluída no modelo de elementos finitos através de um elemento de mola na extremidade do varão (Fig. 15), que é definido pelo modelo constitutivo apresentado na Fig. 15b. A força máxima transmitida por esta mola(Fau) é:
\[F_{au} = \beta \cdot A_s \cdot f_{yd}\]
onde :
β o coeficiente de ancoragem baseado no tipo de ancoragem,
a secção transversal do varão de reforço,
fyd o valor de projeto (valor calculado) da tensão de cedência da armadura.
Model verification
Structural verifications according to Eurocode
Assessment of the structure using CSFM is performed by two different analyses: one for serviceability, and one for ultimate limit state load combinations. The serviceability analysis assumes that the ultimate behavior of the element is satisfactory, and the yield conditions of the material will not be reached at serviceability load levels. This approach enables the use of simplified constitutive models (with a linear branch of concrete stress-strain diagram) for serviceability analysis to enhance numerical stability and calculation speed.
Structural verifications according to ACI 318-19
Assessment of the structure using the CSFM is performed by two different analyses: one for serviceability, and one for strength load combinations. The serviceability analysis assumes that the behavior under factored loads is satisfactory, and the yield conditions of the material will not be reached at serviceability load levels. This approach enables the use of simplified constitutive models (with a linear branch of concrete stress-strain diagram) for serviceability analysis to enhance numerical stability and calculation speed.
CSFM is in accordance with ACI 318-19, chapter 6.8.1.1. In order for the CSFM to meet the requirements from ACI 318-19 Section 6.8.1.2, a lot of verification testing was done at various universities. Individual articles summarizing the results of verification and validation can be found at the following link.
Structural verifications according to Australian standard AS 3600 (2018)
Assessment of the structure using the CSFM is performed by two different analyses: one for serviceability, and one for strength load combinations. The serviceability analysis assumes that the behavior under factored loads is satisfactory, and the yield conditions of the material will not be reached at serviceability load levels. This approach enables the use of simplified constitutive models (with a linear branch of concrete stress-strain diagram) for serviceability analysis to enhance numerical stability and calculation speed.
The CSFM is a structural analysis method that satisfies the general rules in Chapters 6.1.1 and 6.1.2 and is defined as (f) non-linear stress analysis in Chapter 6.1.3 - further in Chapter 6.6.
The analysis by CSFM takes into account all relevant non-linear and inelastic effects (except shrinkage) defined in 6.6.3.
In order to satisfy the requirements in Sections 6.6.4 and 6.6.5 - more can be found in AS3600:2018 Sup 1:2022 Section C6.6 - verification and validations of the method were done at various universities. Individual articles summarizing the results of verification and validation can be found at the following link.
Since IDEA StatiCa Detail is a practical design program, factored characteristic compressive cylinder strength at 28 days f'c is used for calculations, as is described in the next chapter.
Prestressing - model description
References
ACI Committee 318. 2019. Building Code Requirements for Structural Concrete (ACI 318-19) and Commentary. Farmington Hills, MI: American Concrete Institute.
Alvarez, Manuel. 1998. Einfluss des Verbundverhaltens auf das Verformungsvermögen von Stahlbeton. IBK Bericht 236. Basel: Institut für Baustatik und Konstruktion, ETH Zurich, Birkhäuser Verlag.
Beeby, A. W. 1979. “The Prediction of Crack Widths in Hardened Concrete.” The Structural Engineer 57A (1): 9–17.
Broms, Bengt B. 1965. “Crack Width and Crack Spacing In Reinforced Concrete Members.” ACI Journal Proceedings 62 (10): 1237–56. https://doi.org/10.14359/7742.
Burns, C.. 2012. “Serviceability Analysis of Reinforced Concrete Members Based on the Tension Chord Model.” IBK Report Nr. 342, Zurich, Switzerland: ETH Zurich.
Crisfield, M. A. 1997. Non-Linear Finite Element Analysis of Solids and Structures. Wiley.
European Committee for Standardization (CEN). 2015. 1 Eurocode 2: Design of concrete structures - Part 1-1: General rules and rules for buildings. Brussels: CEN, 2005.
Fernández Ruiz, M., and A. Muttoni. 2007. “On Development of Suitable Stress Fields for Structural Concrete.” ACI Structural Journal 104 (4): 495–502.
Kaufmann, W., J. Mata-Falcón, M. Weber, T. Galkovski, D. Thong Tran, J. Kabelac, M. Konecny, J. Navratil, M. Cihal, and P. Komarkova. 2020. “Compatible Stress Field Design Of Structural Concrete. Berlin, Germany.”AZ Druck und Datentechnik GmbH, ISBN 978-3-906916-95-8.
Kaufmann, W., and P. Marti. 1998. “Structural Concrete: Cracked Membrane Model.” Journal of Structural Engineering 124 (12): 1467–75. https://doi.org/10.1061/(ASCE)0733-9445(1998)124:12(1467).
Kaufmann, W.. 1998. “Strength and Deformations of Structural Concrete Subjected to In-Plane Shear and Normal Forces.” Doctoral dissertation, Basel: Institut für Baustatik und Konstruktion, ETH Zürich. https://doi.org/10.1007/978-3-0348-7612-4.
Konečný, M., J. Kabeláč, and J. Navrátil. 2017. Use of Topology Optimization in Concrete Reinforcement Design. 24. Czech Concrete Days (2017). ČBS ČSSI. https://resources.ideastatica.com/Content/06_Detail/Verification/Articles/Topology_optimization_US.pdf.
Marti, P. 1985. “Truss Models in Detailing.” Concrete International 7 (12): 66–73.
Marti, P. 2013. Theory of Structures: Fundamentals, Framed Structures, Plates and Shells. First edition. Berlin, Germany: Wiley Ernst & Sohn.
http://sfx.ethz.ch/sfx_locater?sid=ALEPH:EBI01&genre=book&isbn=9783433029916.
Marti, P., M.Alvarez, W. Kaufmann, and V. Sigrist. 1998. “Tension Chord Model for Structural Concrete.” Structural Engineering International 8 (4): 287–298.
https://doi.org/10.2749/101686698780488875.
Mata-Falcón, J. 2015. “Serviceability and Ultimate Behaviour of Dapped-End Beams (In Spanish: Estudio Del Comportamiento En Servicio y Rotura de Los Apoyos a Media Madera).” PhD thesis, Valencia: Universitat Politècnica de València.
Meier, H. 1983. “Berücksichtigung Des Wirklichkeitsnahen Werkstoffverhaltens Beim Standsicherheitsnachweis Turmartiger Stahlbetonbauwerke.” Institut für Massivbau, Universität Stuttgart.
Navrátil, J., P. Ševčík, L. Michalčík, P. Foltyn, and J. Kabeláč. 2017. A Solution for Walls and Details of Concrete Structures. 24. Czech Concrete Days.
Schlaich, J., K. Schäfer, and M. Jennewein. 1987a. “Toward a Consistent Design of Structural Concrete.” PCI Journal 32 (3): 74–150.
Standards Australia. 2018. Concrete Structures (AS 3600:2018). Sydney, NSW: Standards Australia.
Standards Australia. 2022. Concrete Structures – Commentary (Supplement 1 to AS 3600:2018). Sydney, NSW: Standards Australia.
Vecchio, F.J., and M.P. Collins. 1986. “The Modified Compression Field Theory for Reinforced Concrete Elements Subjected to Shear.” ACI Journal 83 (2): 219–31.