Vergelijking van IDEA StatiCa met ANSYS
Inleiding
Het doel van deze vergelijking is om aan te tonen dat de resultaten van IDEA StatiCa vergelijkbaar of veilig zijn in vergelijking met algemene eindige-elementen softwarevan derden. Er is gekozen voor ANSYS-software [1], die als bewezen en betrouwbaar wordt beschouwd. Het ANSYS-model is gemaakt en geëvalueerd door prof. ing. Jiří Kala, Ph.D. aan de Technische Universiteit van Brno, Tsjechië.
Twee geselecteerde verbindingen werden geselecteerd en gemodelleerd in ANSYS, release 19.2, en IDEA StatiCa Connection, release 21.1.4.
ANSYS-model
Er zijn meerdere manieren om stalen verbindingen te modelleren. Het doel was om te controleren of de eindige elementen die in het IDEA StatiCa model worden gebruikt werken zoals bedoeld. Daarom is het model in ANSYS gemaakt met de bedoeling om het automatisch gemaakte model in IDEA StatiCa na te bootsen. Terwijl dit vrij eenvoudig is voor platen, is het erg ingewikkeld voor lassen en bouten, omdat deze speciale eindige elementen bevatten die de weerstand en belasting-vervormingseigenschappen van bouten en lassen simuleren volgens de codes, zoals Code of Practice for the Structural Use of Steel 2011 [2]. Ze zijn ook verbonden met de platen door een geavanceerd samenstel van meerpuntsbeperkingen en andere aanvullende elementen.
Het ANSYS-model is gemaakt met schelpelementen SHELL 181 in de middellijn. SHELL 181 is een 4-knoops isoparametrisch schaalelement met zes vrijheidsgraden in elke knoop. Er werden vijf integratielagen langs de dikte van de schaal gebruikt. Platen, lassen, boutkoppen en moeren werden gesimuleerd door dit element met von Mises rekgrens. De vloeigrens van platen was 275 MPa voor stalen platen met een dikte kleiner dan of gelijk aan 16 mm en 265 MPa voor platen met een dikte groter dan 16 mm.
Simulatie van lasverbindingen is een moeilijke taak. Een gecombineerd lasmodel opgesteld door Turlier [3] werd gebruikt. Het bestaat uit een hellend schaalelement dat de las simuleert. De dikte en breedte zijn gelijk aan de dikte van de keel. Verder bevat het schaalelementen met een elastisch materiaalmodel die het hellende schaalelement verbinden met het net van de schaalelementen die platen simuleren door de plaatdikte heen. Het Von Mises vloeicriterium wordt gewoonlijk gecontroleerd voor het hellende schaalelement van de las. Het is niet ideaal voor de vergelijking omdat het ontwerplasmodel vereenvoudigd is en sommige spanningen in de las niet worden aangenomen.
Figuur 1: Gecombineerd lasmodel
Een contact wordt beschreven door een paar elementen CONTA 174 en TARGE 170 tussen het oppervlak van de eindplaat en de kolomflens en ook tussen de boutkop (moer) en de platen. Een contactalgoritme Augmented Lagrange methode en contact zoeken op plaatsen van Gauss punten werd gebruikt. Wrijvingscoëfficiënt 0,3 werd gebruikt. Het verschil tussen wrijvingsloos contact is klein. Omdat er geen voorspanning van bouten wordt verondersteld, beweegt de eindplaat aanvankelijk, bij kleine belastingsstappen, naar beneden en wordt door bouten tegengehouden wanneer de contactspanning nog steeds erg laag is. De oppervlakte-oppervlakte variant van het flexibele contact werd gebruikt.
De bout werd gemodelleerd met BEAM 188 element met elastisch materiaal en bijbehorend oppervlak. De bout is aan beide uiteinden gefixeerd in de schaalelementen die een boutkop en een moer simuleren. Extra elementen zorgen voor de positie van de bout in de boutgaten in platen.
Er werden meerdere varianten gemaakt met verschillende contactinstellingen. Een contact is van nature een geometrisch niet-lineaire eigenschap. Er werd een oplossing gevonden voor een analyse met grote vervormingen, waarbij de evenwichtsvergelijkingen worden bijgewerkt op een vervormd model; er werd echter ook een oplossing gevonden voor een analyse met kleine vervormingen. Contacten met wrijvingscoëfficiënten 0,3 en 0,0 werden uitgeprobeerd. Deze varianten dienden om het risico op onnauwkeurigheden van de numerieke analyse te kwantificeren en te minimaliseren. Bovengenoemde varianten gaven coherente en vergelijkbare resultaten. Gedetailleerde beoordeling werd gedaan met slechts één model dat betrouwbaar is en overeenkomt met de methoden van het vergeleken IDEA StatiCa model.
Sparse matrix direct solver werd gebruikt voor de analyse. De niet-lineaire analyse gebruikt de volledige Newton-Raphson methode. Automatische selectie van belastingsstappen werd gebruikt. De initiële belasting komt overeen met 0,01 van de toegepaste belasting, de minimale en maximale belastingstap is respectievelijk 0,002 en 1. Het maximale aantal iteraties in elke stap is 22.
Voorbeeld 1
Voorbeeld 1 is een ligger-kolomverbinding. De balkdoorsnede is UB 686 x 254 x 125. De kolomdoorsnede is UC 356 x 406 x 235 en is aan beide uiteinden bevestigd. Staalkwaliteit S275 wordt gebruikt voor alle balken en platen. De verbinding is ontworpen als eindplaat met acht bouten M45 kwaliteit 10.9. De verdisconteerde belasting op de balk in de verbinding wordt berekend:
- My = 920 kNm
- Vz = 460 kN
ANSYS model
Het ANSYS-model heeft een kolom met een lengte van 5 216 mm, wat overeenkomt met het IDEA StatiCa-model. De kolom is aan beide uiteinden gefixeerd. De ligger is gemodelleerd als een uitkragende ligger met een lengte van 2 000 mm (van knooppunt tot uiteinde) en wordt belast door een neerwaartse kracht van 460 kN, die gelijkmatig is verdeeld over de knooppunten die de liggerconstructie simuleren. In tegenstelling tot het IDEA StatiCa-model worden de kolom en de ligger over de hele lengte gemaakt door schaalelementen. In IDEA StatiCa wordt alleen de verbinding gemaakt door schaalelementen. Voor de rest van de elementen worden de gecondenseerde elementen gebruikt.
43 076 SHELL 181 elementen werden gebruikt om het model te maken. Het rekenmodel had 259 326 vergelijkingen met een breedte van 144. Er waren 12 substappen en 31 iteraties nodig om de analyse te voltooien.
Figuur 2: ANSYS schaalmodel - het algemene beeld
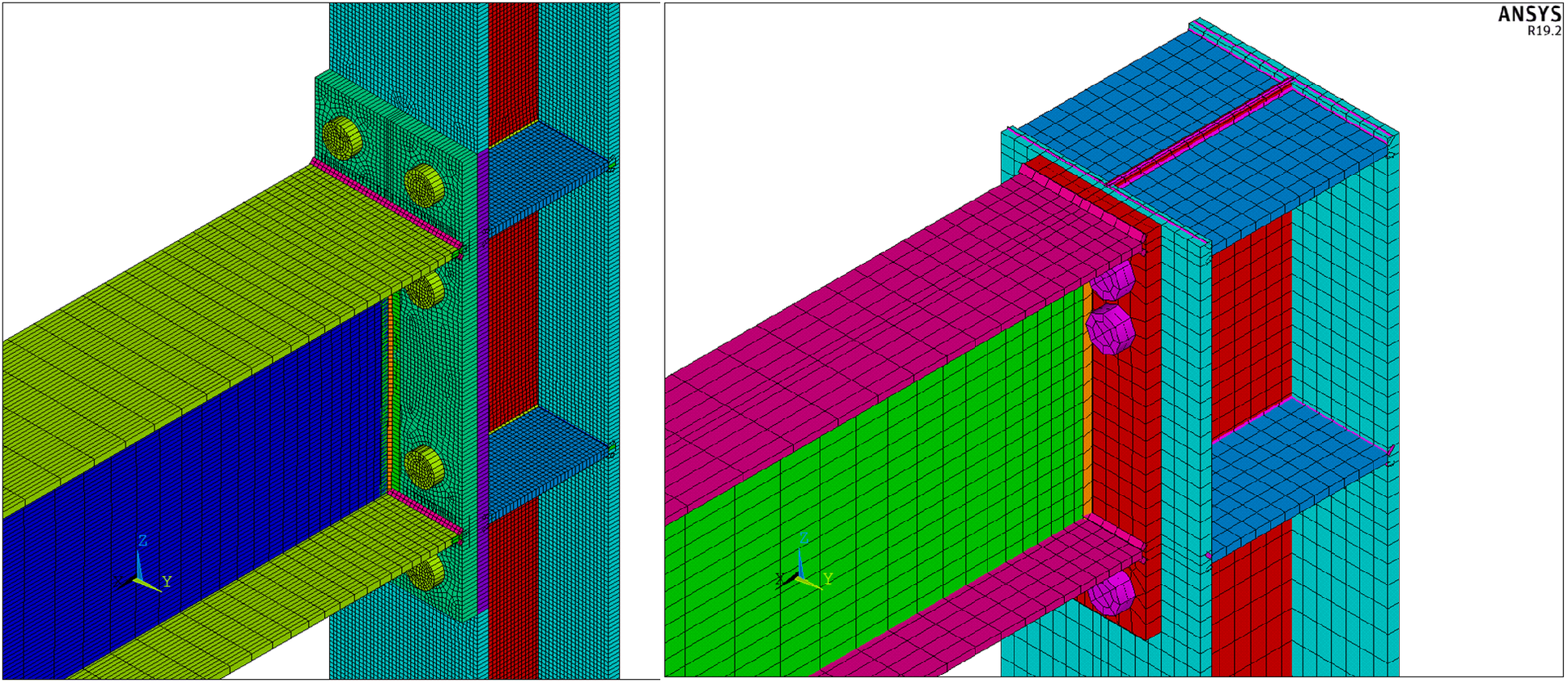
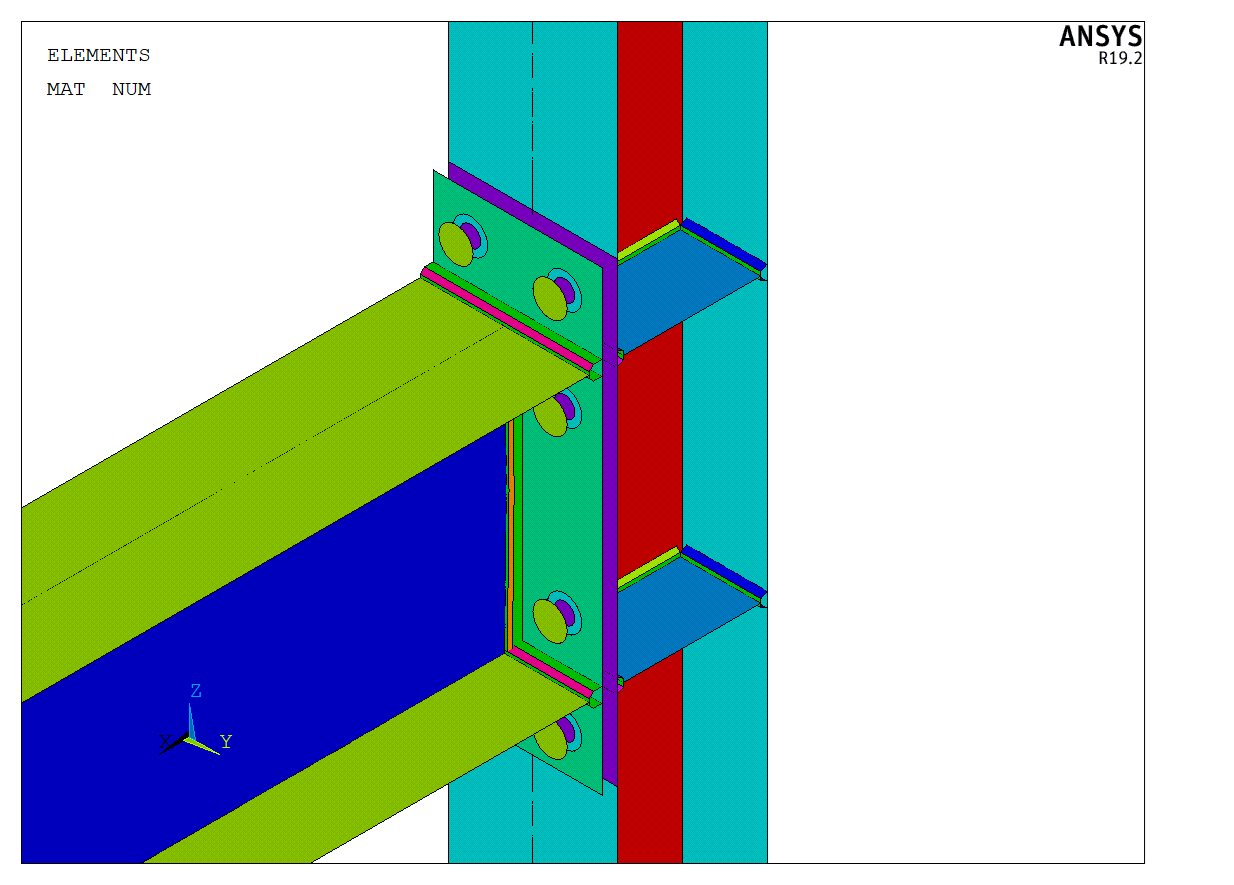
Figuur 3: Detail van de verbinding
Figuur 4: Detail van lassen en bouten
Figuur 5: Schaalelementen weergegeven met hun dikte - zijaanzicht
Figuur 6: Schaalelementen weergegeven met hun dikte - axonometrie
Vergelijking van resultaten
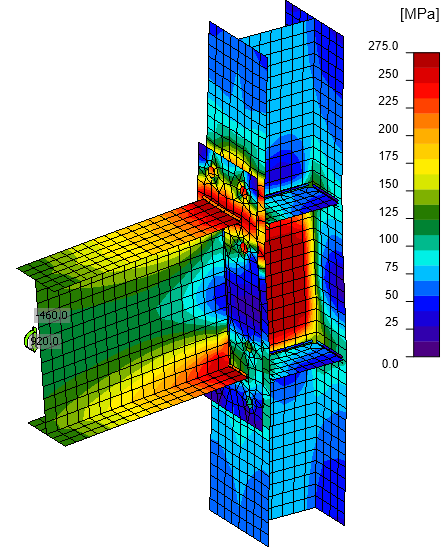
Figuur 7: ANSYS model - von Mises spanning - axonometrie
Figuur 8: IDEA StatiCa model - von Mises spanning - axonometrie
Figuur 9: ANSYS model - von Mises spanning - zijaanzicht
Figuur 10: IDEA StatiCa model - von Mises spanning - zijaanzicht
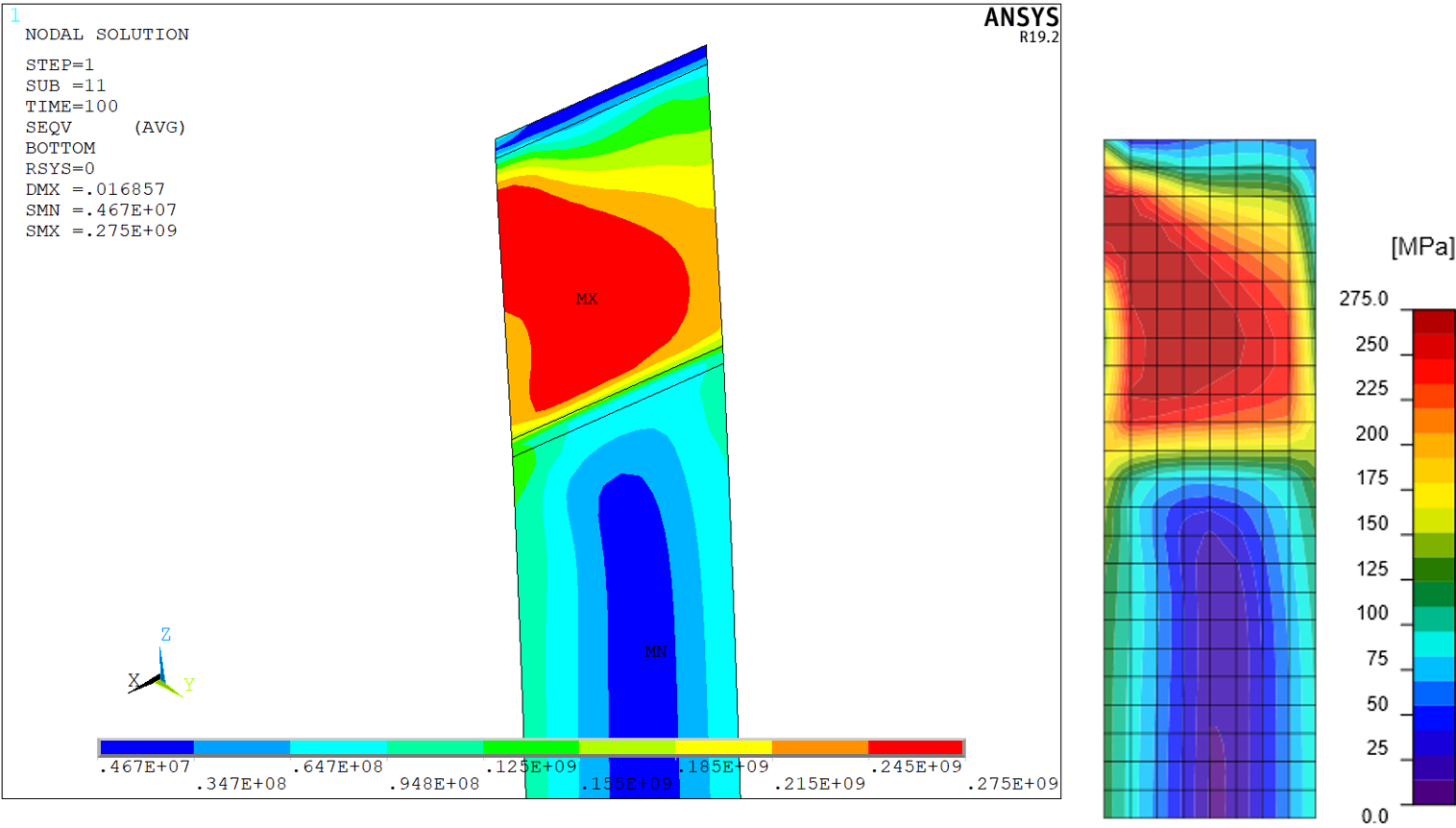
Figuur 11: Kolom achterflens - von Mises spanning
Figuur 12: Kolom voorflens (bij eindplaat) - von Mises spanning
Figuur 13: Kolom lijf - von Mises spanning
Figuur 14: Eindplaat - von Mises spanning
Figuur 15: Kolomverstijvers (doorgaande platen)
De verdeling van von Mises-spanningen in beide modellen is bijna identiek. Kleine verschillen worden toegeschreven aan fijnere mazen in het ANSYS-model en verschillen in de modellering van bouten, lassen en contacten. Merk op dat IDEA StatiCa een constante schaal gebruikt, maar dat de schaal in ANSYS varieert.
De piekspanningen zijn ook erg vergelijkbaar, zoals te zien is in de volgende tabellen. Een iets groter verschil zit in de piek plastische rek van de eindplaat. Ook dit wordt veroorzaakt door fijnere mesh en verschillen in de modellering van bouten en lassen.
Tabel 1: Spanningen en rek bij platen - ANSYS
| Materiaal | Dikte [mm] | \(\sigma) [MPa] | \varepsilon_{pl} \) [-] | |
| C-bfl1 | S275 | 30.2 | 265 | 0.3 |
| C-tfl1 | S275 | 30.2 | 214 | |
| C-w1 | S275 | 18.4 | 265 | 0.1 |
| b-bfl1 | S275 | 16.2 | 265 | 0.07 |
| B-tfl1 | S275 | 16.2 | 265 | 0.05 |
| B-w1 | S275 | 11.7 | 275 | 0.01 |
| EP1 | S275 | 40 | 267 | 0.9 |
| STIFF1a | S275 | 18 | 201 | |
| STIFF1b | S275 | 18 | 201 | |
| STIFF1c | S275 | 18 | 118 | |
| STIFF1d | S275 | 18 | 118 |
Tabel 2: Spanningen en rek bij platen - IDEA StatiCa
De verschillen zijn groter in het geval van bouten. In IDEA StatiCa zijn de boutkrachten in twee bovenste rijen altijd hoger. Dat wordt veroorzaakt door het optreden van wrikkrachten. Dat wordt hoogstwaarschijnlijk veroorzaakt door de hogere stijfheid van bouten in IDEA StatiCa in trek en een stijver contact. De wrikkrachten in IDEA StatiCa hebben de neiging af te nemen wanneer bouten zwaarder worden belast, bouten meegeven, meer vervormen en de spanningen in contacten afnemen. Het gedrag van T-stub in IDEA StatiCa en het optreden van wrikrachten wordt hier als voorbeeld beschreven. De verschillen tussen de dwarskrachten kunnen worden toegeschreven aan het verschil tussen de contacten. Het contact in het ANSYS-model is met de algemeen gebruikte wrijvingscoëfficiënt 0,3. Aan de andere kant gebruikt IDEA StatiCa wrijvingsloos contact, wat de veiligste aanname is.
Tabel 3: Krachten in bouten - ANSYS
| Trekkracht [kN] | Schuifkracht [kN] | |
| B1 | 304 | 83 |
| B2 | 304 | 83 |
| B3 | 334 | 44 |
| B4 | 334 | 44 |
| B5 | 34.6 | 71 |
| B6 | 34.6 | 71 |
| B7 | 37.1 | 37 |
| B8 | 37.1 | 37 |
Tabel 4: Krachten in bouten - IDEA StatiCa
De lasnaden zijn moeilijk te evalueren in ANSYS vanwege de aanwezigheid van spanningen die in het ontwerp worden verwaarloosd. Er werd echter een goede overeenstemming bereikt tussen IDEA StatiCa en ANSYS. Over het algemeen zijn de spanningen bij belangrijke lassen, zoals lassen tussen liggers en eindplaten, in IDEA StatiCa iets hoger, wat betekent dat het ontwerp veiliger is. In het geval van sommige verstijvingslassen werden de spanningen in ANSYS hoger gevonden.
Tabel 5: Spanningen in lassen - vergelijking van ANSYS en IDEA StatiCa
| Onderdeel | Rand | a [mm] | ANSYS fw [MPa] | IDEA StatiCa fw [MPa] |
| EP1 | B-bfl 1 | ◢10.0◣ | 202.1 | 217.6 |
| ◢10.0◣ | 207.5 | 218.4 | ||
| EP1 | B-tfl 1 | ◢10.0◣ | 214.1 | 217.5 |
| ◢10.0◣ | 196.4 | 216.6 | ||
| EP1 | B-w 1 | ◢6.0◣ | 215.1 | 218.2 |
| ◢6.0◣ | 215.1 | 218.2 | ||
| C-bfl 1 | STIFF1a | ◢8.0◣ | 106.3 | 144.6 |
| ◢8.0◣ | 206.2 | 190.6 | ||
| C-w 1 | STIFF1a | ◢8.0◣ | 201.1 | 68.6 |
| ◢8.0◣ | 61.0 | 65.9 | ||
| C-tfl 1 | STIFF1a | ◢8.0◣ | 90.4 | 76.3 |
| ◢8.0◣ | 65.1 | 60.8 | ||
| C-bfl 1 | STIFF1b | ◢8.0◣ | 195.1 | 191.8 |
| ◢8.0◣ | 129.2 | 145.5 | ||
| C-w 1 | STIFF1b | ◢8.0◣ | 207.1 | 65.9 |
| ◢8.0◣ | 63.6 | 68.7 | ||
| C-tfl 1 | STIFF1b | ◢8.0◣ | 110.0 | 60.8 |
| ◢8.0◣ | 86.5 | 76.3 | ||
| C-bfl 1 | STIFF1c | ◢8.0◣ | 157.5 | 162.2 |
| ◢8.0◣ | 135.2 | 158.1 | ||
| C-w 1 | STIFF1c | ◢8.0◣ | 29.4 | 67.6 |
| ◢8.0◣ | 28.2 | 65.8 | ||
| C-tfl 1 | STIFF1c | ◢8.0◣ | 54.4 | 51.8 |
| ◢8.0◣ | 74.4 | 66.5 | ||
| C-bfl 1 | STIFF1d | ◢8.0◣ | 137.6 | 159.8 |
| ◢8.0◣ | 161.1 | 163.7 | ||
| C-w 1 | STIFF1d | ◢8.0◣ | 87.9 | 65.8 |
| ◢8.0◣ | 92.4 | 67.6 | ||
| C-tfl 1 | STIFF1d | ◢8.0◣ | 65.4 | 66.5 |
| ◢8.0◣ | 54.2 | 51.8 |
Voorbeeld 2
Voorbeeld 2 is een balk-kolomverbinding. De balk heeft een doorsnede UB 356 x 127 x 33. De kolom heeft een doorsnede UC 254 x 254 x 73 en is aan de onderkant bevestigd. Alle gebruikte staalsoorten zijn S275. De eindplaatverbinding is voorzien van zes bouten M24 kwaliteit 8.8. De verdisconteerde belasting op de ligger in de verbinding is berekend:
- My = 100 kNm
- Vz = 100 kN
ANSYS model
Het ANSYS-model heeft een kolom met een lengte van 1 606 mm, wat overeenkomt met het IDEA StatiCa-model. De kolom is aan de onderkant gefixeerd. De ligger is gemodelleerd als een uitkragende ligger met een lengte van 1 000 mm (van knooppunt tot uiteinde) en wordt belast door een neerwaartse kracht van 100 kN die gelijkmatig verdeeld is over de knooppunten die de liggerconstructie simuleren. In tegenstelling tot het IDEA StatiCa-model worden de kolom en de ligger over de hele lengte gemaakt met schaalelementen.
5 036 SHELL 181 elementen werden gebruikt om het model te maken. Dat leidde tot 25 152 vergelijkingen met een matrixbreedte van 126. Om de analyse te voltooien waren 11 substappen en 22 iteraties nodig.
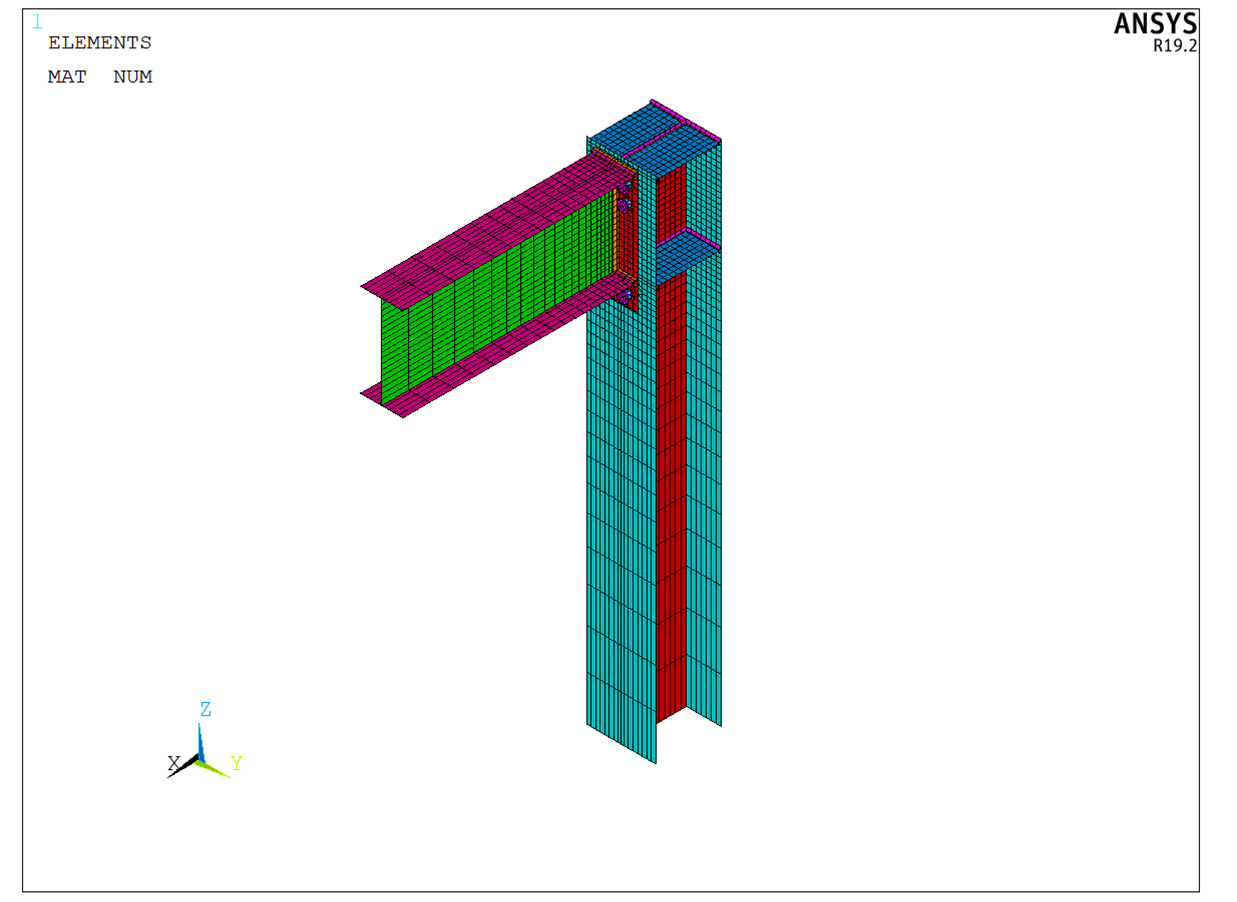
Figuur 16: ANSYS model - axonometrie
Figuur 17: ANSYS model - detail bij verbinding
Figuur 18: ANSYS model - met schaalelement dikte
Figuur 19: ANSYS model - zijaanzicht met schaalelementdikte
Figuur 20: ANSYS model - zijaanzicht met schelpelementdikte - detail van de verbinding
Vergelijking van resultaten
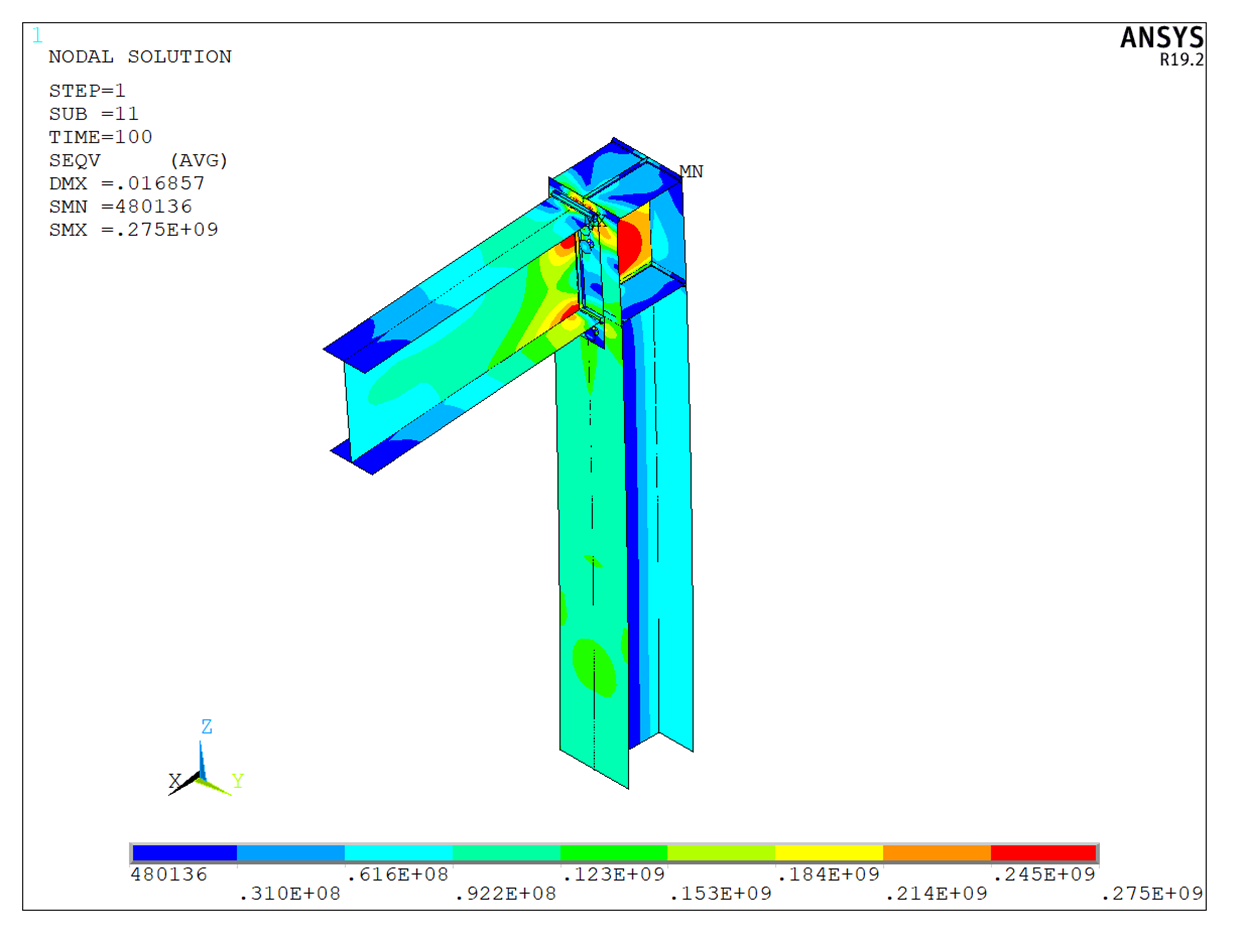
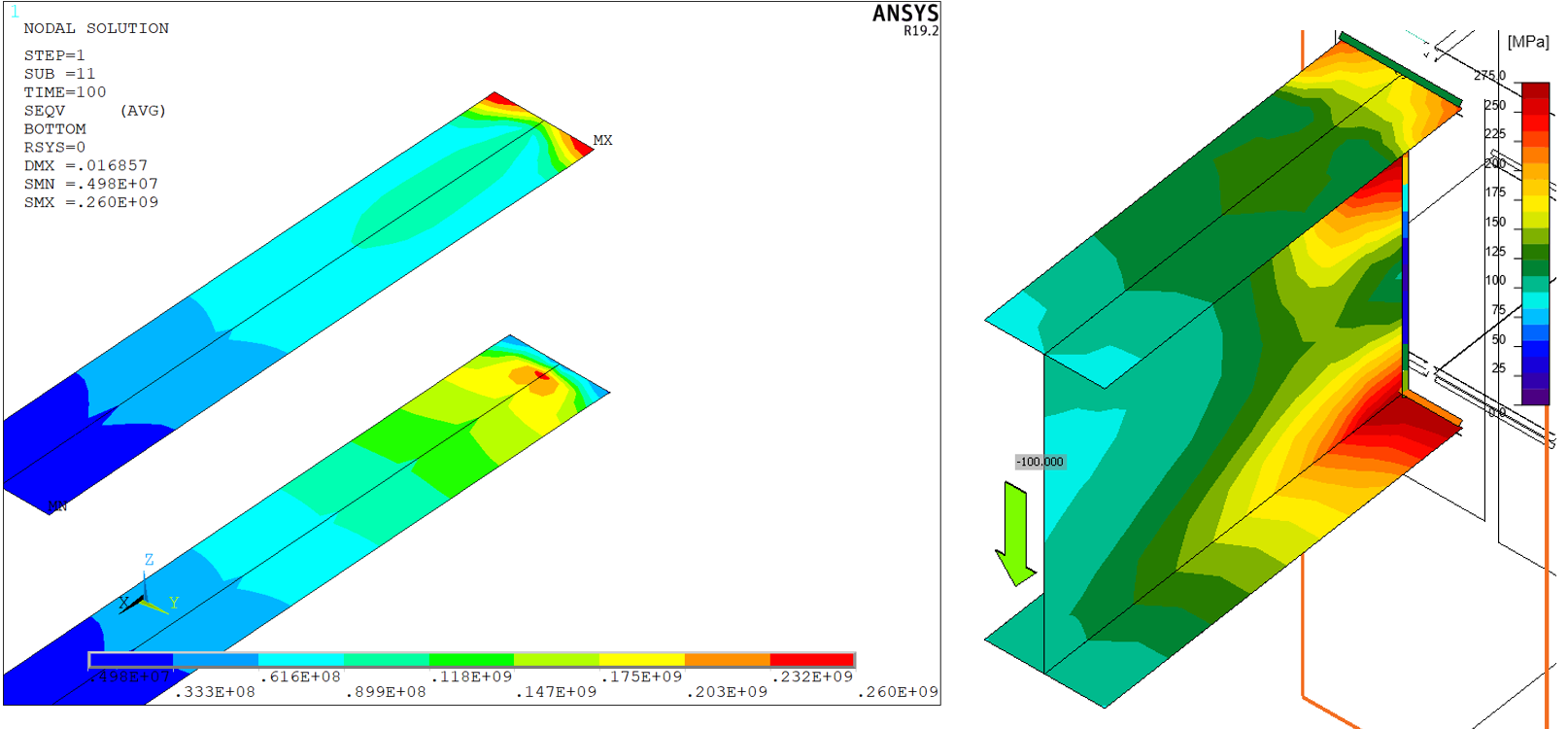
Figuur 21: ANSYS - Axonometrie - von Mises spanning
Figuur 22: IDEA StatiCa - Axonometrie - von Mises spanning
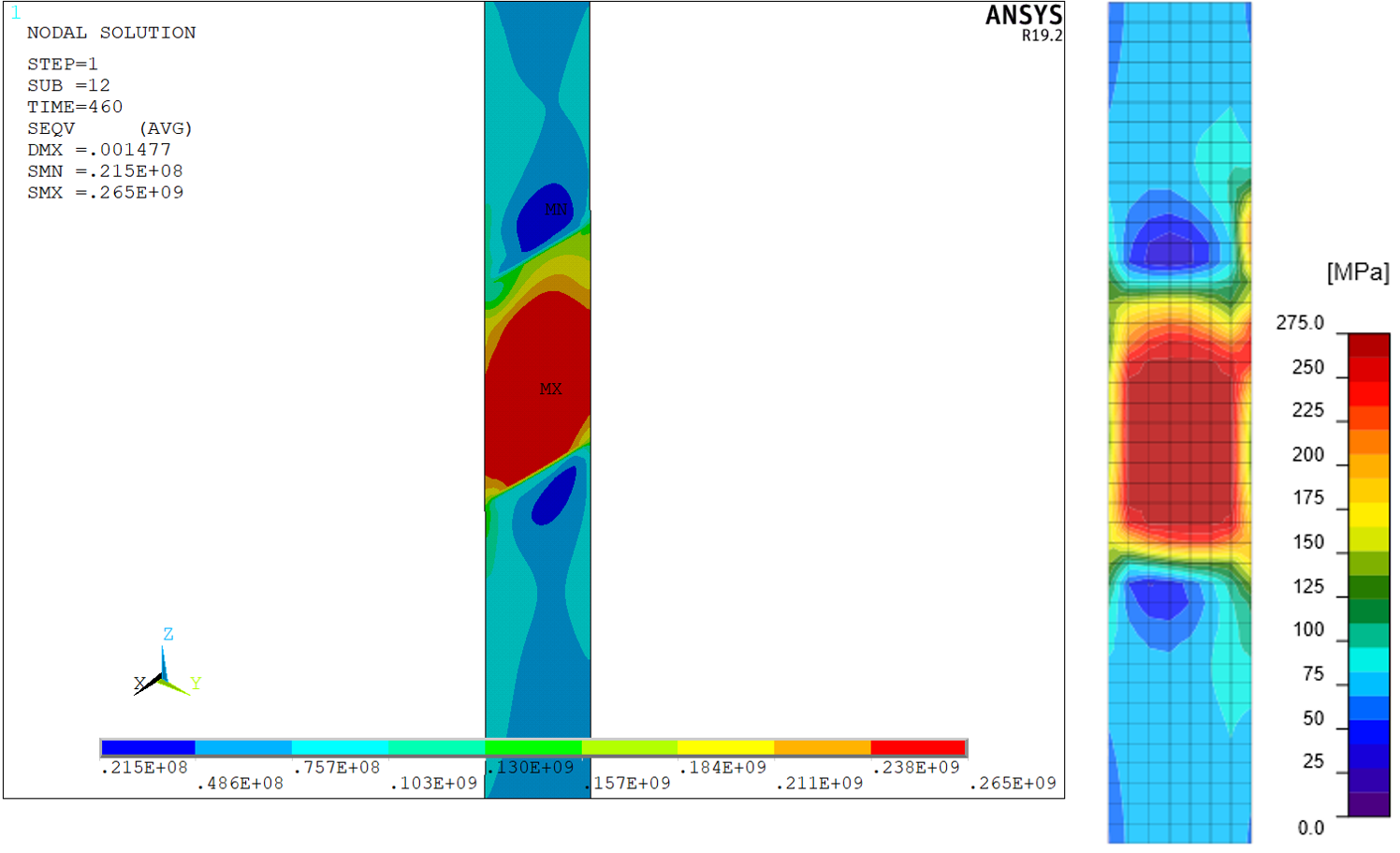
Figuur 23: Kolomflens bij eindplaat - von Mises spanning
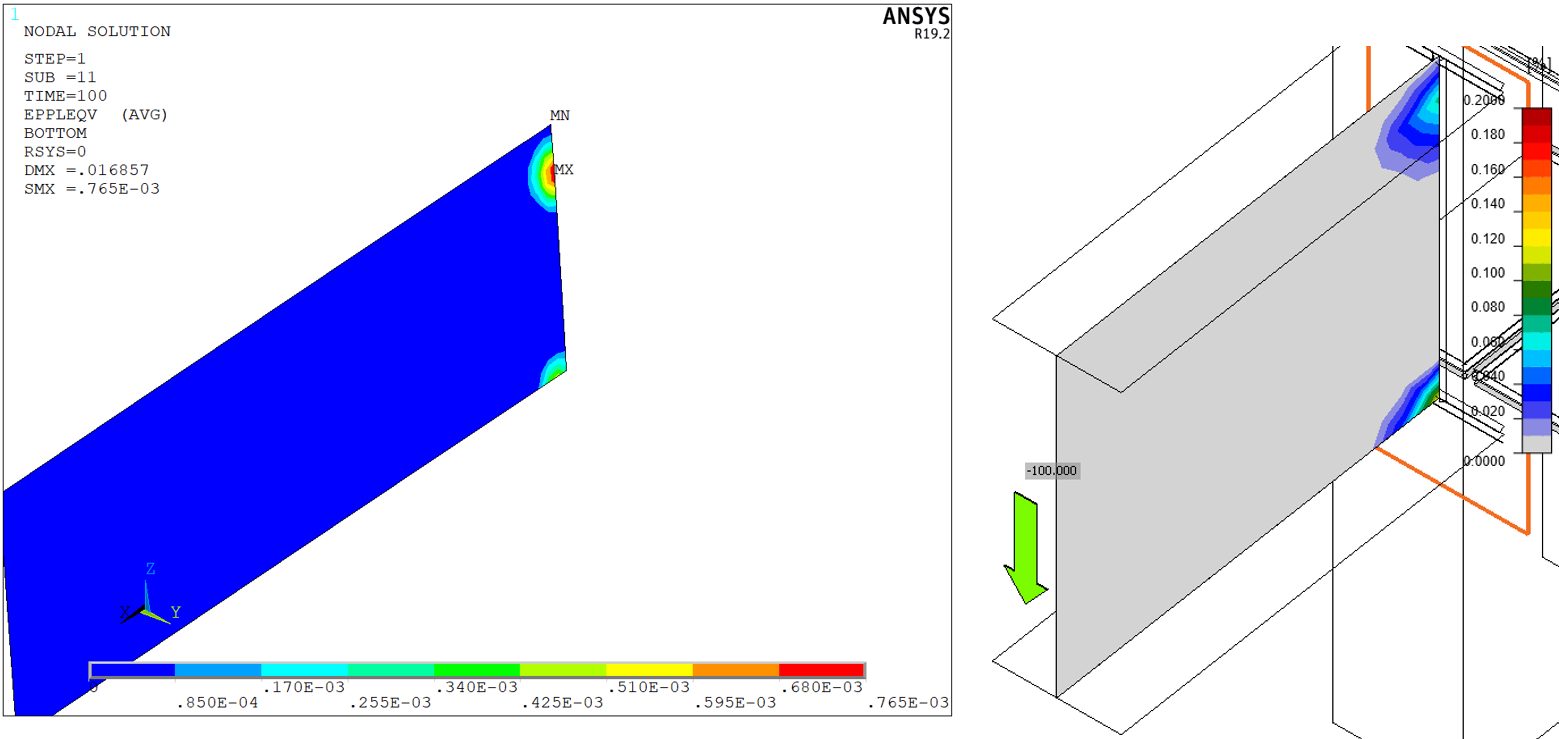
Figuur 24: Kolomflens bij eindplaat - plastische rek
Figuur 25: Kolom web - von Mises spanning
Figuur 26: Kolom verstijvers - von Mises spanning
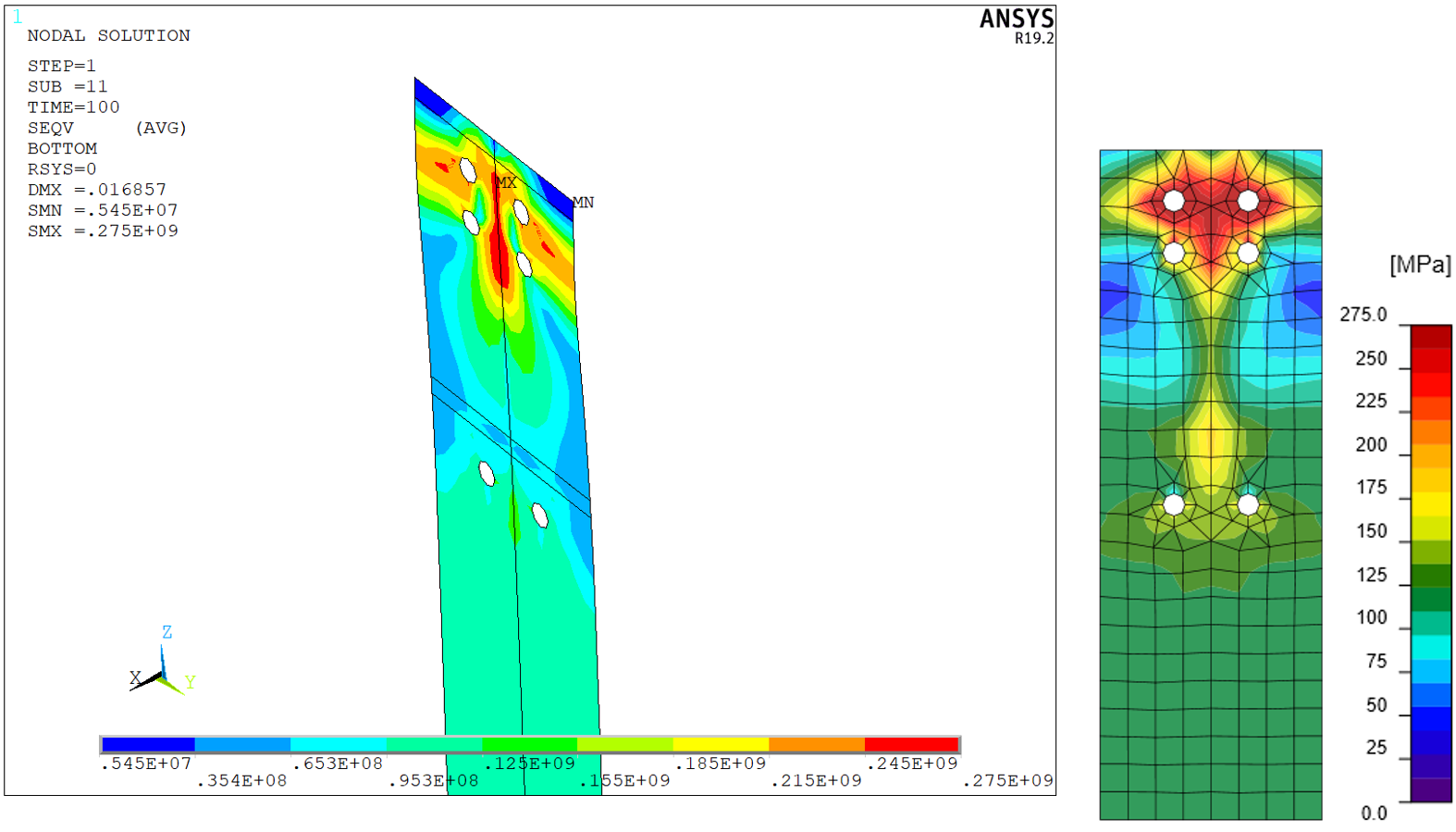
Figuur 27: Eindplaat - von Mises spanning
Figuur 28: Ligger flenzen - von Mises spanning
Afbeelding 29: Ligger web - von Mises spanning
Afbeelding 30: Liggerplaat - plastische spanningen
De verdeling van von Mises-spanningen in beide modellen is bijna identiek. Kleine verschillen worden toegeschreven aan fijnere mazen in het ANSYS-model en verschillen in de modellering van bouten, lassen en contacten. Merk op dat IDEA StatiCa een constante schaal gebruikt, maar dat de schaal in ANSYS varieert.
De piekspanningen zijn ook erg vergelijkbaar, zoals te zien is in de volgende tabellen. Een iets groter verschil zit in de piek plastische rek van de eindplaat. Ook dit wordt veroorzaakt door fijnere mesh en verschillen in de modellering van bouten en lassen.
Tabel 6: Spanningen en rek bij platen - ANSYS
| Materiaal | Dikte [mm] | \(\sigma) [MPa] | \(\varepsilon_{pl}) [-] | |
| C-bfl1 | S275 | 14.2 | 174 | |
| C-tfl1 | S275 | 14.2 | 275 | 0.386 |
| C-w 1 | S275 | 8.6 | 275 | 0.026 |
| B-bfl 1 | S275 | 8.5 | 246 | |
| B-tfl1 | S275 | 8.5 | 260 | |
| B-w1 | S275 | 6 | 275 | 0.077 |
| EP2 | S275 | 20 | 264 | |
| Stijf1a | S275 | 10 | 155 | |
| Stijf1b | S275 | 10 | 155 | |
| Stijf1c | S275 | 10 | 264 | |
| Stijf1d | S275 | 10 | 264 |
Tabel 7: Spanningen en rek bij platen - IDEA StatiCa
Tabel 8: Krachten in bouten - ANSYS
| Trekkracht | Schuifkracht | |
| B1 | 104.2 | 14.7 |
| B2 | 104.2 | 14.7 |
| B3 | 47.1 | 14.3 |
| B4 | 47.1 | 14.3 |
| B5 | 12.1 | 21 |
| B6 | 12.1 | 21 |
Tabel 9: Krachten en controles van bouten - IDEA StatiCa
De verschillen zijn groter in het geval van bouten. In IDEA StatiCa zijn de boutkrachten altijd hoger, behalve voor de onderste rij bouten. Dat wordt veroorzaakt door het optreden van wrikkrachten. Dit wordt hoogstwaarschijnlijk veroorzaakt door de hogere stijfheid van bouten in IDEA StatiCa in trek en een stijver contact. De wrikkrachten in IDEA StatiCa hebben de neiging af te nemen wanneer bouten zwaarder worden belast, bouten meegeven, meer vervormen en de spanningen in contacten afnemen. De verschillen tussen de dwarskrachten kunnen worden toegeschreven aan het verschil tussen de contacten. Het contact in het ANSYS-model heeft de algemeen gebruikte wrijvingscoëfficiënt van 0,3. Aan de andere kant gebruikt IDEA StatiCa wrijvingsloos contact, wat de veiligste aanname is.
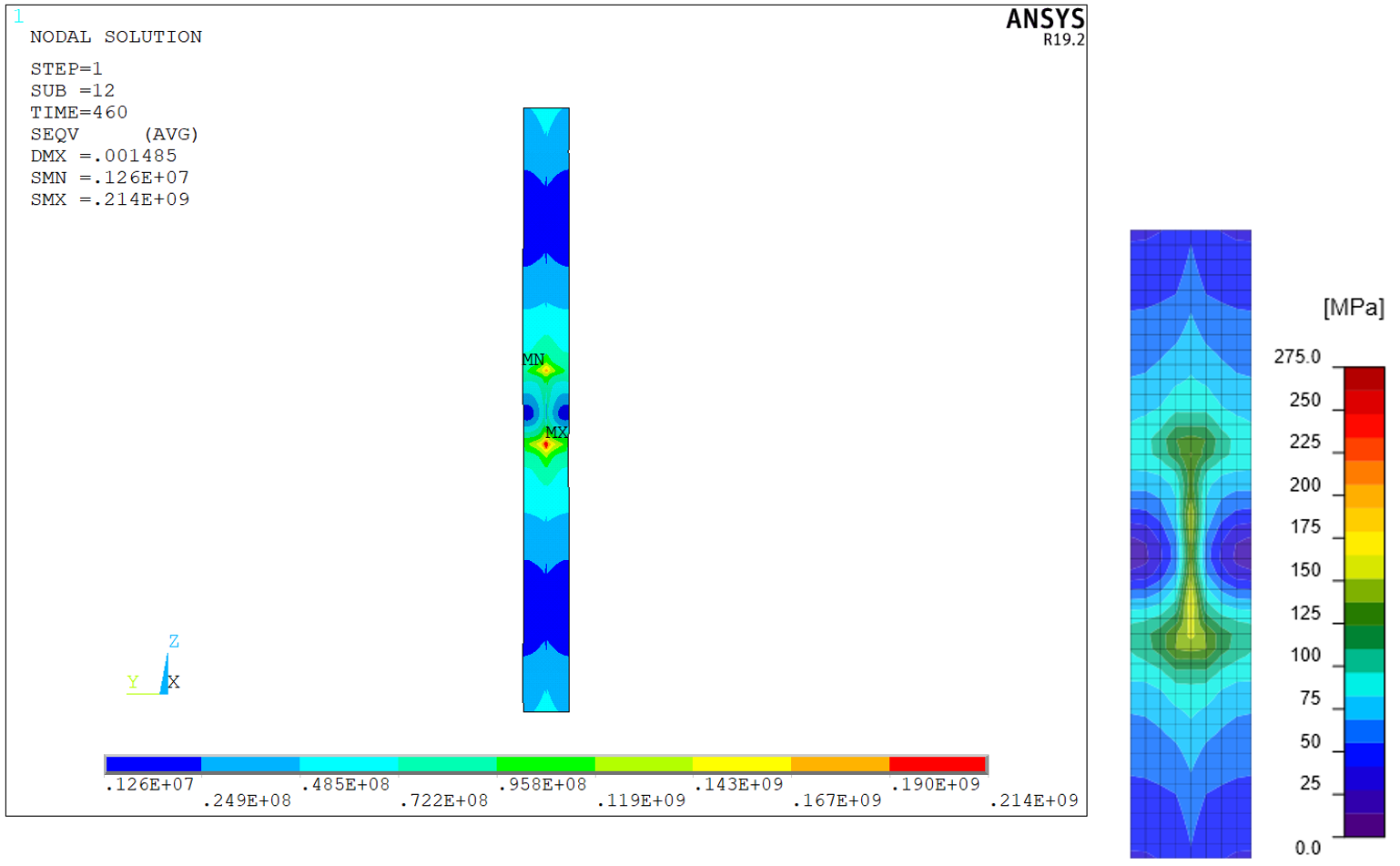
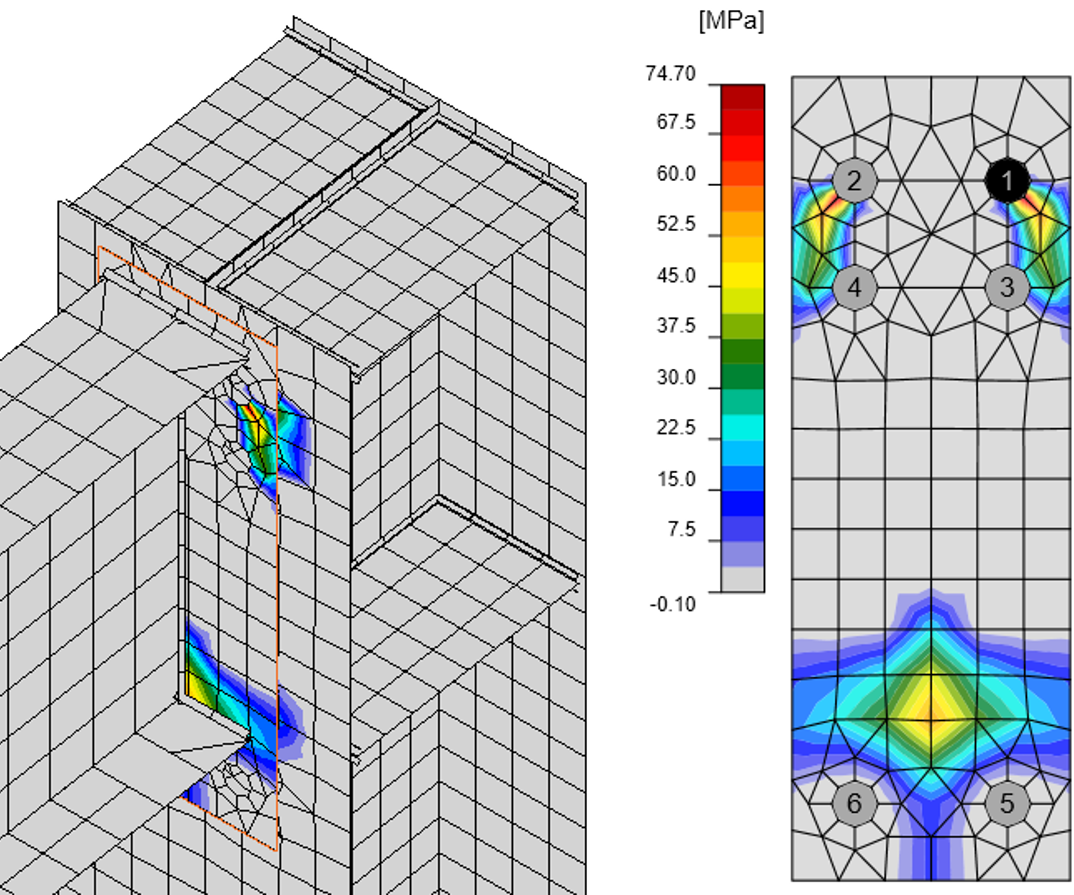
Figuur 31: Contactspanningen tussen eindplaat en kolomflens in ANSYS
Figuur 32: Contactspanningen tussen eindplaat en kolomflens in IDEA StatiCa
De lasnaden zijn moeilijk te evalueren in ANSYS vanwege de aanwezigheid van spanningen die in het ontwerp worden verwaarloosd. Er werd echter een goede overeenkomst bereikt tussen IDEA StatiCa en ANSYS. Over het algemeen zijn de spanningen in IDEA StatiCa iets hoger, wat betekent dat het ontwerp veiliger is.
Tabel 10: Spanningen in lassen
| Lid | Las | a [mm] | ANSYS fw [MPa] | IDEA StatiCa fw [MPa] |
| EP2 | B-bfl 1 | ◢6.0◣ | 218.0 | 215.7 |
| ◢6.0◣ | 166.5 | 215.7 | ||
| EP2 | B-tfl 1 | ◢6.0◣ | 129.2 | 120.7 |
| ◢6.0◣ | 88.3 | 135.9 | ||
| EP2 | B-w 1 | ◢5.0◣ | 219.1 | 215.6 |
| ◢5.0◣ | 219.1 | 215.6 | ||
| C-bfl 1 | STIFF1a | ◢4.0◣ | 40.8 | 41.5 |
| ◢4.0◣ | 60.8 | 57.3 | ||
| C-w 1 | STIFF1a | ◢4.0◣ | 47.5 | 61.2 |
| ◢4.0◣ | 37.9 | 57.5 | ||
| C-tfl 1 | STIFF1a | ◢4.0◣ | 167.1 | 137.2 |
| ◢4.0◣ | 111.0 | 105.7 | ||
| C-bfl 1 | STIFF1b | ◢4.0◣ | 62.7 | 57.2 |
| ◢4.0◣ | 41.8 | 41.4 | ||
| C-w 1 | STIFF1b | ◢4.0◣ | 47.5 | 57.6 |
| ◢4.0◣ | 66.4 | 61.2 | ||
| C-tfl 1 | STIFF1b | ◢4.0◣ | 120.2 | 105.4 |
| ◢4.0◣ | 167.4 | 136.9 | ||
| C-bfl 1 | STIFF1c | ◢4.0◣ | 58.8 | 32.2 |
| ◢4.0◣ | 30.8 | 30.8 | ||
| C-w 1 | STIFF1c | ◢4.0◣ | 83.2 | 80.9 |
| ◢4.0◣ | 65.4 | 82.4 | ||
| C-tfl 1 | STIFF1c | ◢4.0◣ | 174.0 | 215.8 |
| ◢4.0◣ | 164.3 | 214.3 | ||
| C-bfl 1 | STIFF1d | ◢4.0◣ | 19.6 | 30.8 |
| ◢4.0◣ | 20.9 | 32.2 | ||
| C-w 1 | STIFF1d | ◢4.0◣ | 73.9 | 82.4 |
| ◢4.0◣ | 96.6 | 80.9 | ||
| C-tfl 1 | STIFF1d | ◢4.0◣ | 163.3 | 214.0 |
| ◢4.0◣ | 173.6 | 215.8 |
Samenvatting
Twee ligger-kolom verbindingen zijn ontworpen in IDEA StatiCa en vergeleken met ANSYS. Staalverbindingen kunnen op veel manieren gemodelleerd worden. Het doel was niet om verschillende modelleertechnieken te vergelijken, maar om het IDEA StatiCa berekeningsmodel te verifiëren. Daarom werd een vergelijkbare modelleertechniek gebruikt in ANSYS - schaalelementen voor platen en lassen, en balkelementen voor bouten. Mesh was dichter in ANSYS model en het bevatte geen speciale elementen, zoals multipoint constraints of elementen met faalcriteria gebaseerd op codes, in dit geval de Hong Kong code. De verschillen tussen de modellen van ANSYS en IDEA StatiCa worden toegeschreven aan deze verschillen in modellering. De verschillen zijn echter zeer klein; de spannings- en plastische vervormingspatronen zijn bijna identiek. Het grootste verschil zit in de boutkrachten, waar IDEA StatiCa hogere trekkrachten geeft, dus veiligere resultaten dan ANSYS. Spanningen in lassen zijn moeilijk te bepalen in tegenstelling tot IDEA StatiCa waar speciale eindige elementen worden gebruikt die voldoen aan de ontwerpeisen van de code. Over het algemeen was er een goede overeenkomst tussen de lasspanningen. De lasspanningen waren iets hoger in IDEA StatiCa, wat betekent dat het ontwerp veilig is.
Referenties
[1] Ansys® Mechanical Enterprise, release 19.2
[2] Hong Kong Buildings Department, Code of Practice for Structural Use of Steel 2011 (Editie 2021), beschikbaar op https://www.bd.gov.hk/doc/en/resources/codes-and-references/code-and-design-manuals/SUOS2011.pdf.
[3] Turlier D., Klein P., Bérard F. ¨Seam Sim¨ methode voor de beoordeling van de constructie van naadlassen binnen een globale structuur-FEA. Proc. Int. Conf. IIW2010 Istanbul (Turkije). AWST 651-658, 2010.