IDEA StatiCa Detail – Structural design of concrete discontinuities
The theoretical background is based on COMPATIBLE STRESS FIELD DESIGN OF STRUCTURAL CONCRETE
(Kaufmann et al., 2020)
Structural design of concrete discontinuities in IDEA StatiCa Detail
Introduction to the CSFM method
General introduction for the structural design of concrete details
Main assumptions and limitations
Design tools for reinforcement
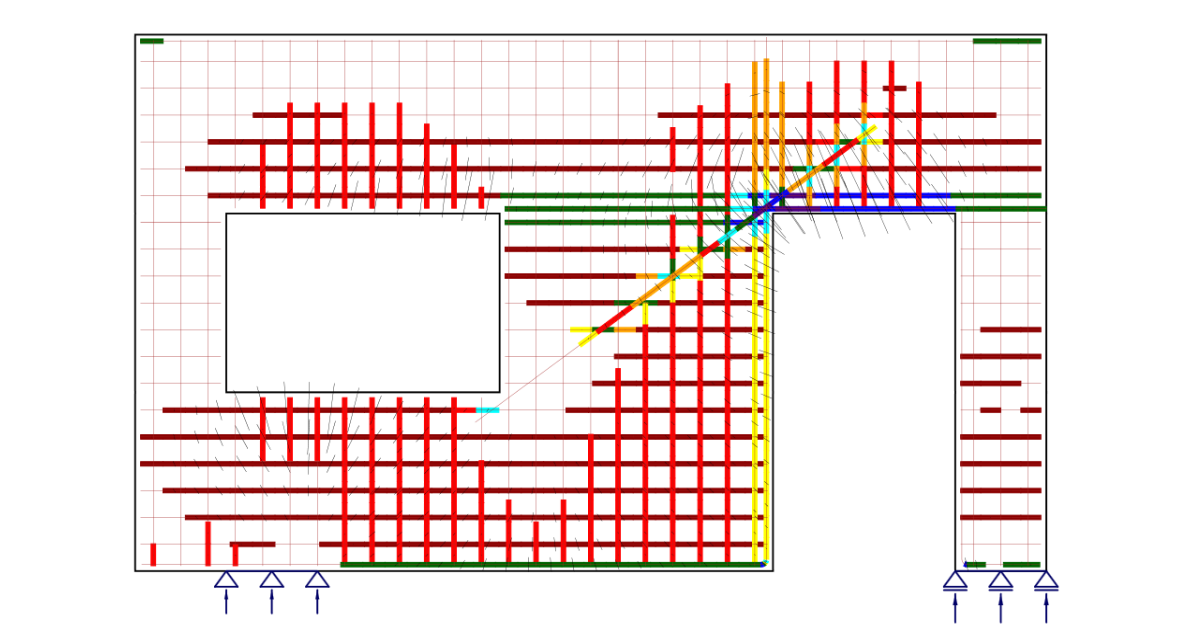
Analysis model of IDEA StatiCa Detail
Introduction to finite element implementation
Supports and load transmitting components
Load transfer at trimmed ends of beams
Geometric modification of cross-sections
Finite element types
Meshing
Solution method and load-control algorithm
Presentation of results
Model verification
Limit states, crack width calculation, and Tension stiffening
Structural verifications according to EUROCODE
- Material models (EN)
- Safety factors
- Ultimate limit state analysis
- Partially loaded areas (PLA)
- Serviceability limit state analysis
Structural verifications according to ACI 318-19
- Material models (ACI)
- Strength reduction and load factors
- Strength verifications
- Bearing and anchorage zones - Partially loaded areas
- Serviceability verifications
Prestressing in Detail - Model description
Introduction to the CSFM method
Analysis model of IDEA StatiCa Detail
Introducción a la aplicación de elementos finitos
El CSFM considera campos de tensión continuos en el hormigón (elementos finitos 2D), complementados por elementos discretos de "varilla" que representan la armadura (elementos finitos 1D). Por lo tanto, la armadura no se incrusta difusamente en los elementos finitos 2D del hormigón, sino que se modela explícitamente y se conecta a ellos. En el modelo de cálculo se considera un estado de tensiones plano.
\[ \textsf{\textit{footnotesize{Fig. 6\qquad Visualización del modelo de cálculo de un elemento estructural (viga recortada) en Idea StatiCa Detail.}}]
Se pueden modelizar tanto muros y vigas enteras, como detalles (partes) de vigas (región de discontinuidad aislada, también llamada extremo recortado). En el caso de muros y vigas enteras, los apoyos deben definirse de tal manera que resulte una estructura (externamente) isostática (estáticamente determinada) o hiperestática (estáticamente indeterminada). La transferencia de carga en los extremos recortados de las vigas se introduce mediante una zona de transferencia especial de Saint-Venant, que garantiza una distribución de tensiones realista en la región de detalle analizada.
Finite element types
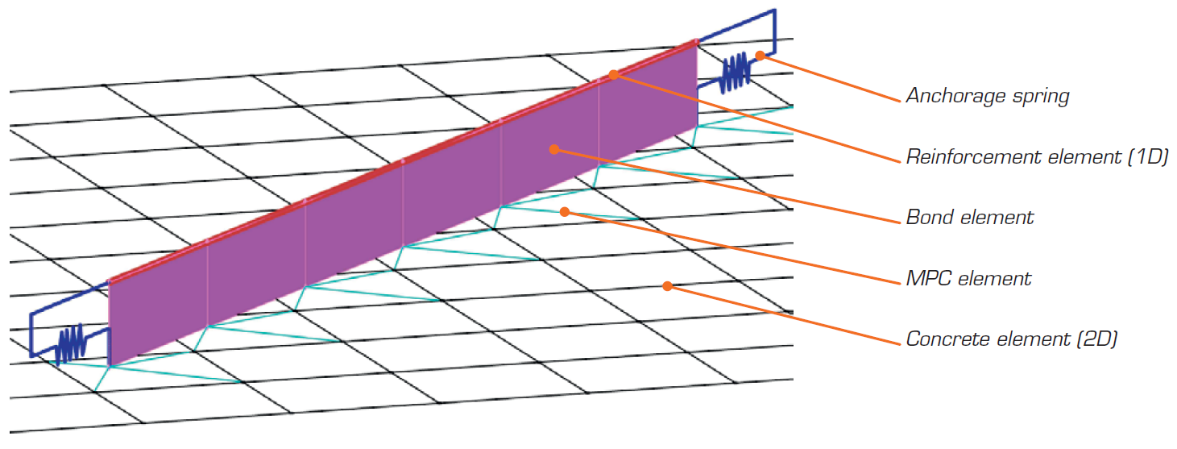
The non-linear (inelastic) finite element analysis model is created by several types of finite elements used to model concrete, reinforcement, and the bond between them. Concrete and reinforcement elements are first meshed independently and then connected to each other using multi-point constraints (MPC elements). This allows the reinforcement to occupy an arbitrary, relative position in relation to the concrete. If anchorage length verification is to be calculated, bond and anchorage end spring elements are inserted between the reinforcement and the MPC elements.
\[ \textsf{\textit{\footnotesize{Fig. 13\qquad Finite element model: reinforcement elements mapped to concrete mesh using MPC elements and bond elements.}}}\]
Concrete
Concrete is modeled using quadrilateral and trilateral shell elements, CQUAD4 and CTRIA3. These can be defined by four or three nodes, respectively. Only plane stress is assumed to exist in these elements, i.e., stresses or strains in the z-direction are not considered.
Each element has four or three integration points which are placed at approximately 1/4 of its size. At each integration point in every element, the directions of principal strains α1, α2 are calculated. In both of these directions, the principal stresses σc1, σc2 and stiffnesses E1, E2 are evaluated according to the specified concrete stress-strain diagram, as per Fig. 2. It should be noted that the impact of the compression softening effect couples the behavior of the main compressive direction to the actual state of the other principal direction.
Reinforcement
Rebars are modeled by two-node 1D “rod” elements (CROD), which only have axial stiffness. These elements are connected to special “bond” elements which were developed in order to model the slip behavior between a reinforcing bar and the surrounding concrete. These bond elements are subsequently connected by MPC (multi-point constraint) elements to the mesh representing the concrete. This approach allows the independent meshing of reinforcement and concrete, while their interconnection is ensured later.
Bond elements
The anchorage length is verified by implementing the bond shear stresses between concrete elements (2D) and reinforcing bar elements (1D) in the finite element model. To this end, a “bond” finite element type was developed.
The definition of the bond element is similar to that of a shell element (CQUAD4). It is also defined by 4 nodes, but in contrast to a shell, it only has a non-zero stiffness in shear between the two upper and two lower nodes. In the model, the upper nodes are connected to the elements representing reinforcement and the lower nodes to those representing concrete. The behavior of this element is described by the bond stress, τb, as a bilinear function of the slip between the upper and lower nodes, δu, see Fig. 14.
\[ \textsf{\textit{\footnotesize{Fig. 14\qquad (a) conceptual illustration of the deformation of a bond element; (b) a stress-deformation function.}}}\]
The elastic stiffness modulus of the bond-slip relationship, Gb, is defined as follows:
\[G_b = k_g \cdot \frac{E_c}{Ø}\]
where:
kg coefficient depending on the reinforcing bar surface (by default kg = 0.2)
Ec modulus of elasticity of concrete (taken as Ecm in case of EN)
Ø the diameter of the reinforcing bar
The design values (factored values) of ultimate bond shear stress, fbd, provided in the respective selected design codes EN 1992-1-1 or ACI 318-19 are used to verify the anchorage length. The hardening of the plastic branch is calculated by default as Gb/105.
Anchorage spring
The provision of anchorage ends to the reinforcing bars (i.e., bends, hooks, loops…), which fulfills the prescriptions of design codes, allows the reduction of the basic anchorage length of the bars (lb,net) by a certain factor β (referred to as the ‘anchorage coefficient’ below). The design value of the anchorage length (lb) is then calculated as follows:
\[l_b = \left(1 - \beta\right)l_{b,net}\]
The intended reduction in lb,net is equivalent to the activation of the reinforcing bar at its end at a percentage of its maximum capacity given by the anchorage reduction coefficient, as shown in Fig. 15a.
\[ \textsf{\textit{\footnotesize{Fig. 15\qquad Model for the reduction of the anchorage length:}}}\]
\[ \textsf{\textit{\footnotesize{(a) anchorage force along the anchorage length of the reinforcing bar; (b) slip-anchorage force constitutive relationship.}}}\]
The reduction of the anchorage length is included in the finite element model by means of a spring element at the end of the bar (Fig. 15), which is defined by the constitutive model shown in Fig. 15b. The maximum force transmitted by this spring (Fau) is:
\[F_{au} = \beta \cdot A_s \cdot f_{yd}\]
where :
β the anchorage coefficient based on anchorage type,
As the cross-section of the reinforcing bar,
fyd the design value (factored value) of the yield strength of the reinforcement.
Model verification
Structural verifications according to Eurocode
Assessment of the structure using CSFM is performed by two different analyses: one for serviceability, and one for ultimate limit state load combinations. The serviceability analysis assumes that the ultimate behavior of the element is satisfactory, and the yield conditions of the material will not be reached at serviceability load levels. This approach enables the use of simplified constitutive models (with a linear branch of concrete stress-strain diagram) for serviceability analysis to enhance numerical stability and calculation speed.
Structural verifications according to ACI 318-19
Assessment of the structure using the CSFM is performed by two different analyses: one for serviceability, and one for strength load combinations. The serviceability analysis assumes that the behavior under factored loads is satisfactory, and the yield conditions of the material will not be reached at serviceability load levels. This approach enables the use of simplified constitutive models (with a linear branch of concrete stress-strain diagram) for serviceability analysis to enhance numerical stability and calculation speed.
CSFM is in accordance with ACI 318-19, chapter 6.8.1.1. In order for the CSFM to meet the requirements from ACI 318-19 Section 6.8.1.2, a lot of verification testing was done at various universities. Individual articles summarizing the results of verification and validation can be found at the following link.
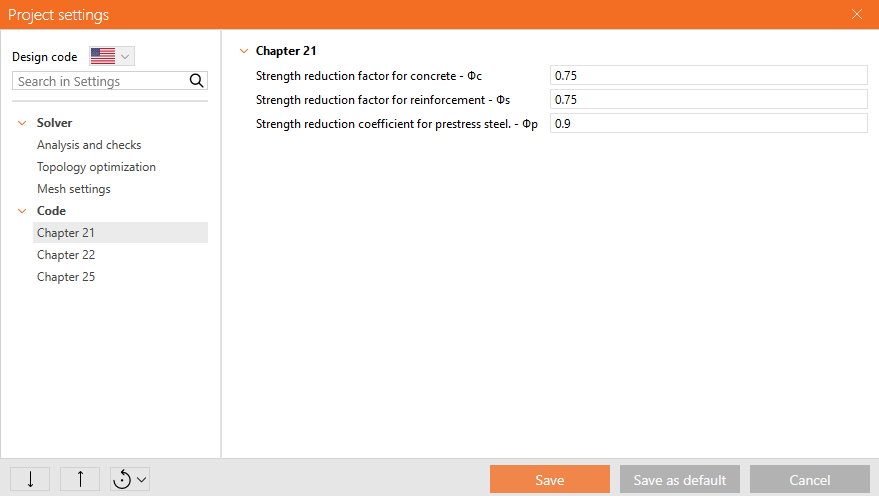
Reducción de la resistencia y factores de carga
El Método del Campo de Tensiones Compatible cumple los códigos de diseño modernos. Dado que los modelos de cálculo sólo utilizan propiedades de material estándar, el formato de factor de seguridad parcial prescrito en los códigos de diseño puede aplicarse sin ninguna adaptación. De este modo, las cargas de entrada se factorizan y las propiedades características del material se reducen utilizando los factores de reducción de resistencia respectivos, exactamente igual que en el análisis convencional del hormigón.
Los valores de los factores de reducción de resistencia se prescriben en ACI 318-19 Cl. 21.2. Los valores por defecto para el hormigón y la armadura se eligen basándose en la suposición de que el ejemplo típico resuelto en la aplicación es a cortante controlado (basado en la Tabla 21.2.1 (b), (f), (g)). Sin embargo, es posible modelizar cualquier tipo de elemento. Por lo tanto, si se evalúa un elemento controlado por compresión o tracción, el usuario tiene la opción de cambiar el valor del factor de reducción de resistencia en las Preferencias.
\[ \textsf{\textit{footnotesize{Fig. 44\qquad Ajuste de los factores de reducción de resistencia en IDEA StatiCa Detail.}}]
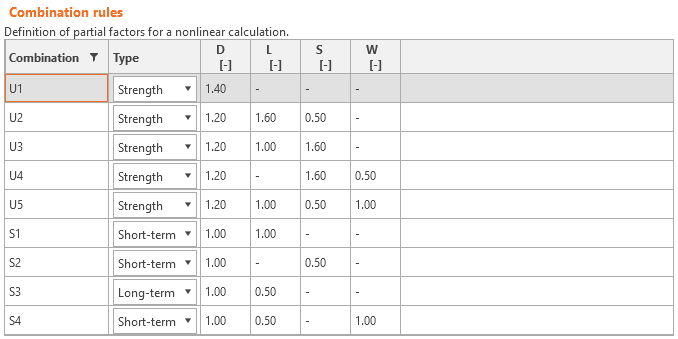
Losfactores de carga para las combinaciones de resistencia se definirán de acuerdo con ACI 318-19 Tabla 5.3.1.
Excepto lo indicado en el Capítulo 34, las combinaciones de carga a nivel de servicio no están definidas en ACI 318-19. Se recomienda utilizar reglas de combinación basadas en el Apéndice C de ASCE/SEI 7-16. Para todas las plantillas, los factores de carga ya están predefinidos.
\[ \textsf{\textit{footnotesize{Fig. 45\qquad La configuración de factores de carga en Idea StatiCa Detail.}}]
Structural verifications according to Australian standard AS 3600 (2018)
Assessment of the structure using the CSFM is performed by two different analyses: one for serviceability, and one for strength load combinations. The serviceability analysis assumes that the behavior under factored loads is satisfactory, and the yield conditions of the material will not be reached at serviceability load levels. This approach enables the use of simplified constitutive models (with a linear branch of concrete stress-strain diagram) for serviceability analysis to enhance numerical stability and calculation speed.
The CSFM is a structural analysis method that satisfies the general rules in Chapters 6.1.1 and 6.1.2 and is defined as (f) non-linear stress analysis in Chapter 6.1.3 - further in Chapter 6.6.
The analysis by CSFM takes into account all relevant non-linear and inelastic effects (except shrinkage) defined in 6.6.3.
In order to satisfy the requirements in Sections 6.6.4 and 6.6.5 - more can be found in AS3600:2018 Sup 1:2022 Section C6.6 - verification and validations of the method were done at various universities. Individual articles summarizing the results of verification and validation can be found at the following link.
Since IDEA StatiCa Detail is a practical design program, factored characteristic compressive cylinder strength at 28 days f'c is used for calculations as is described in the next chapter.
Prestressing - model description
References
ACI Committee 318. 2019. Building Code Requirements for Structural Concrete (ACI 318-19) and Commentary. Farmington Hills, MI: American Concrete Institute.
Alvarez, Manuel. 1998. Einfluss des Verbundverhaltens auf das Verformungsvermögen von Stahlbeton. IBK Bericht 236. Basel: Institut für Baustatik und Konstruktion, ETH Zurich, Birkhäuser Verlag.
Beeby, A. W. 1979. “The Prediction of Crack Widths in Hardened Concrete.” The Structural Engineer 57A (1): 9–17.
Broms, Bengt B. 1965. “Crack Width and Crack Spacing In Reinforced Concrete Members.” ACI Journal Proceedings 62 (10): 1237–56. https://doi.org/10.14359/7742.
Burns, C.. 2012. “Serviceability Analysis of Reinforced Concrete Members Based on the Tension Chord Model.” IBK Report Nr. 342, Zurich, Switzerland: ETH Zurich.
Crisfield, M. A. 1997. Non-Linear Finite Element Analysis of Solids and Structures. Wiley.
European Committee for Standardization (CEN). 2015. 1 Eurocode 2: Design of concrete structures - Part 1-1: General rules and rules for buildings. Brussels: CEN, 2005.
Fernández Ruiz, M., and A. Muttoni. 2007. “On Development of Suitable Stress Fields for Structural Concrete.” ACI Structural Journal 104 (4): 495–502.
Kaufmann, W., J. Mata-Falcón, M. Weber, T. Galkovski, D. Thong Tran, J. Kabelac, M. Konecny, J. Navratil, M. Cihal, and P. Komarkova. 2020. “Compatible Stress Field Design Of Structural Concrete. Berlin, Germany.”AZ Druck und Datentechnik GmbH, ISBN 978-3-906916-95-8.
Kaufmann, W., and P. Marti. 1998. “Structural Concrete: Cracked Membrane Model.” Journal of Structural Engineering 124 (12): 1467–75. https://doi.org/10.1061/(ASCE)0733-9445(1998)124:12(1467).
Kaufmann, W.. 1998. “Strength and Deformations of Structural Concrete Subjected to In-Plane Shear and Normal Forces.” Doctoral dissertation, Basel: Institut für Baustatik und Konstruktion, ETH Zürich. https://doi.org/10.1007/978-3-0348-7612-4.
Konečný, M., J. Kabeláč, and J. Navrátil. 2017. Use of Topology Optimization in Concrete Reinforcement Design. 24. Czech Concrete Days (2017). ČBS ČSSI. https://resources.ideastatica.com/Content/06_Detail/Verification/Articles/Topology_optimization_US.pdf.
Marti, P. 1985. “Truss Models in Detailing.” Concrete International 7 (12): 66–73.
Marti, P. 2013. Theory of Structures: Fundamentals, Framed Structures, Plates and Shells. First edition. Berlin, Germany: Wiley Ernst & Sohn.
http://sfx.ethz.ch/sfx_locater?sid=ALEPH:EBI01&genre=book&isbn=9783433029916.
Marti, P., M.Alvarez, W. Kaufmann, and V. Sigrist. 1998. “Tension Chord Model for Structural Concrete.” Structural Engineering International 8 (4): 287–298.
https://doi.org/10.2749/101686698780488875.
Mata-Falcón, J. 2015. “Serviceability and Ultimate Behaviour of Dapped-End Beams (In Spanish: Estudio Del Comportamiento En Servicio y Rotura de Los Apoyos a Media Madera).” PhD thesis, Valencia: Universitat Politècnica de València.
Meier, H. 1983. “Berücksichtigung Des Wirklichkeitsnahen Werkstoffverhaltens Beim Standsicherheitsnachweis Turmartiger Stahlbetonbauwerke.” Institut für Massivbau, Universität Stuttgart.
Navrátil, J., P. Ševčík, L. Michalčík, P. Foltyn, and J. Kabeláč. 2017. A Solution for Walls and Details of Concrete Structures. 24. Czech Concrete Days.
Schlaich, J., K. Schäfer, and M. Jennewein. 1987a. “Toward a Consistent Design of Structural Concrete.” PCI Journal 32 (3): 74–150.
Vecchio, F.J., and M.P. Collins. 1986. “The Modified Compression Field Theory for Reinforced Concrete Elements Subjected to Shear.” ACI Journal 83 (2): 219–31.