Stützen, die einer hohen Druckbelastung ausgesetzt sind - Passive Umschnürung

Einführung

Der passive Umschnürungseffekt in Betonskonstruktionen bezieht sich auf das Phänomen, dass die Festigkeit und Duktilität von Beton aufgrund des Umschnürungseffekts der umgebenden Materialien, wie z. B. der Verbügelung, verbessert wird. Dieser Effekt ist besonders wichtig für die Erhöhung der Druckfestigkeit von Beton, insbesondere bei hohen Lasten.

Im Folgenden werden die wichtigsten Aspekte der Umschnürungswirkung erläutert:

1. Erhöhte Festigkeit: Die Umschnürung erhöht die Druckfestigkeit des Betons. Wenn seitlicher Druck ausgeübt wird, wird die seitliche Ausdehnung des Betons eingeschrenkt, so dass er höheren axialen Belastungen standhalten kann, bevor er versagt.
2. Erhöhte Duktilität: Eingeschlossener Beton weist eine höhere Duktilität auf, d. h. er kann größere Verformungen ertragen, bevor er versagt.
3. Mechanismen der passiven Umschnürung:
   • Innere Umschnürung: Erreicht wird durch Querbewehrung wie Bügel. Diese Bewehrungen verhindern, dass der Beton reißt und sich nach außen wölbt.
   • Externe Bewehrung: Hierbei handelt es sich um die Verwendung externer Materialien wie faserverstärkte Lamellen oder Stahlmäntel, die um das Bauteil herum angebracht werden. Diese Methode wird häufig für die Nachrüstung und Verstärkung bestehender Strukturen verwendet.
4. Verhalten unter Last: Durch die Umschnürung ändert sich die Versagensart des Betons von einem spröden, plötzlichen Versagen zu einem duktilen, allmählichen Versagen.

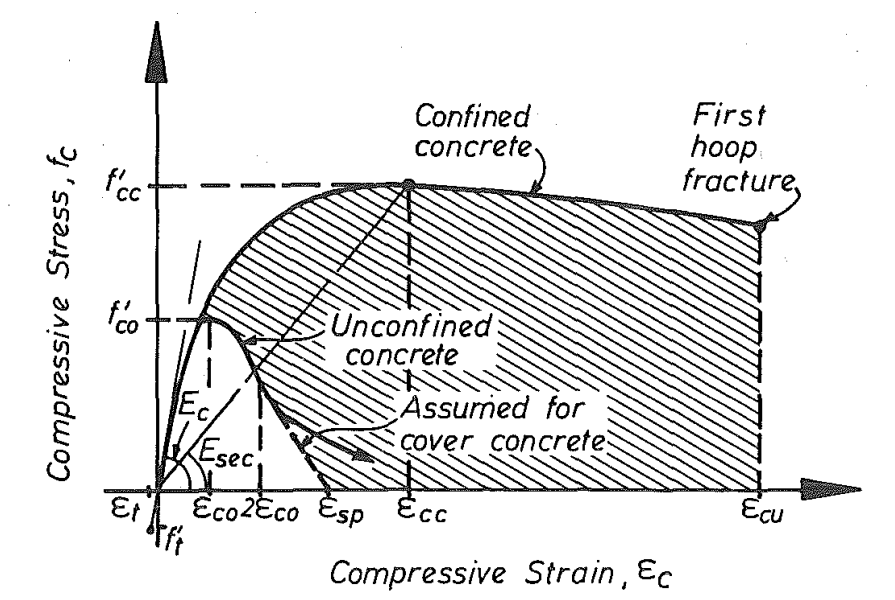
In der folgenden Abbildung können Sie sehen, wie sich das Spannungs-Dehnungs-Diagramm und die Tragfähigkeit mit und ohne Umschnürung unterscheiden können.

\[ \textsf{\textit{\footnotesize{Abb. 1\qquad Vorgeschlagenes Spannungs-Dehnungs-Modell für monotone Belastung mit und ohne Umschnürung [2]}}}\]

Stützen, die einer hohen Druckbelastung ausgesetzt sind - ein Beispiel der passiven Umschnürung

In diesem Beispiel vergleichen wir mehrere unterschiedlich geformte Stützen, die einer hohen Druckbelastung ausgesetzt sind, mit verschiedenen Topologien und Bewehrungsgraden, die in IDEA StatiCa Detail und mit verschiedenen analytischen Ansätzen von Morger et al. [1] berechnet wurden, die in mehreren aktuellen Normen angegeben sind - fib Model Code for Concrete Structures 2010 (MC 2010) [3], SIA 262:2013 Concrete Structures (SIA 262) [4] und Eurocode 2 - Design of concrete structures EN 1992-1-1:2023 (EC 2) [5].

Bevor wir uns mit dem Nachweis selbst beschäftigen, wollen wir die theoretischen Grundlagen von 3D CSFM in Erinnerung rufen, die in der Anwendung IDEA StatiCa Detail implementiert sind - Statische Bemessung von 3D-Diskontinuitäten aus Beton in IDEA StatiCa Detail

Analytische Methoden

Der gesamte Nachweis basiert auf den bereits in [1] erwähnten analytischen Ansätzen. In diesem Text werden wir nur eine grundlegende Beschreibung der analytischen Berechnungsmethoden einschließlich der relevanten Formeln geben. Für ein besseres Verständnis empfehlen wir, die Arbeit [1] genauer zu studieren.

Der Tragwiderstand eines Betonbauteils auf Druck ergibt sich aus der Summe der drei Einzelkomponenten mit ihren zugehörigen Querschnittsflächen: (i) die einachsige Betondruckfestigkeit des gesamten Betonquerschnitts, (ii) die Festigkeit der Längsbewehrung und (iii) die Erhöhung der Betondruckfestigkeit infolge eines dreiachsigen Spannungszustandes durch einschnürende Bewehrung:

\[N_{R}=\underset{(i)}{\underbrace{f_{c}\cdot A_{c}}}+\underset{(ii)}{\underbrace{(f_{sy.l}-f_{c})\cdot A_{s.l}}}+\underset{(iii)}{\underbrace{\Delta f_{conf}\cdot A_{conf}}}\]

wobei f_c = einachsige Betondruckfestigkeit, A_c = Betonquerschnittsfläche, f_sy,l und A_s,l = Streckgrenze und Gesamtquerschnittsfläche der Längsbewehrung, Δf_conf = Betondruckfestigkeitszunahme infolge Umschließung und A_conf = maßgebende Umschließungsbetonfläche.

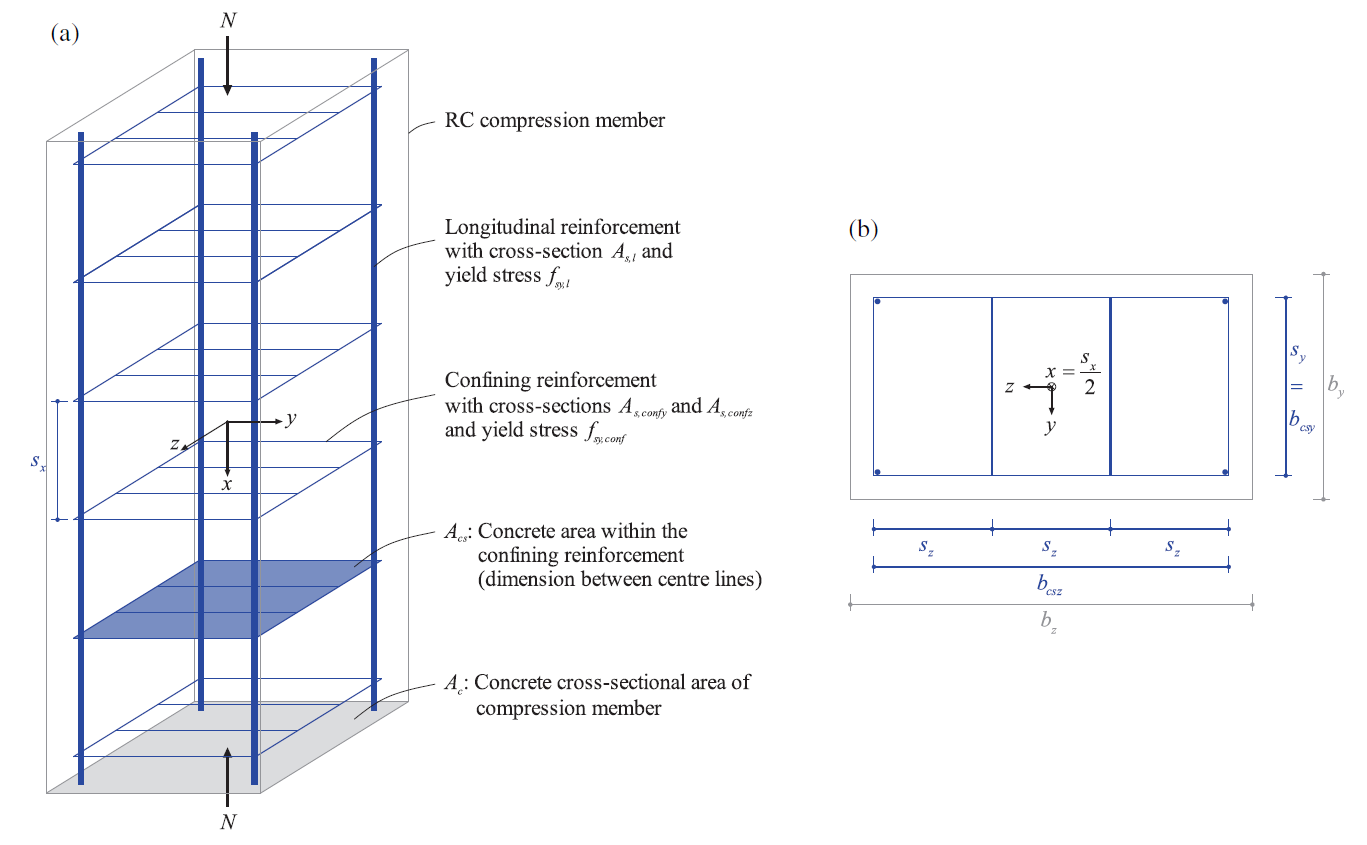
In diesem Artikel wird das Koordinatensystem eines Betonbauteils unter Druck so gewählt, dass die Belastungsrichtung mit der x-Achse zusammenfällt, die als Längsrichtung bezeichnet wird. Die y- und z-Richtung werden daher als Querrichtung bezeichnet.

\[ \textsf{\textit{\footnotesize{Abb. 2\qquad Definition der wichtigsten geometrischen Parameter [1]}}}\]

Die Erhöhung der Betondruckfestigkeit Δf_conf infolge der Umschnürung beträgt etwa das Vierfache der seitlichen Druckspannung [6].

\[\Delta f_{conf}=4\cdot min(\sigma_{confy},\sigma_{confz})\]

Unter der Annahme, dass die umschnürende Bewehrung nachgibt und die einschnürenden Kräfte sich vollständig ausbreiten, folgen die einschnürenden Spannungen dem Gleichgewicht wie folgt:

\[\sigma_{confy}=\frac{\sum A_{s.confy}\cdot f_{sy.conf}}{s_{x}\cdot b_{csz}};\sigma_{confz}=\frac{\sum A_{s.confz}\cdot f_{sy.conf}}{s_{x}\cdot b_{csy}}\]

Dabei ist f_sy.conf die Streckgrenze der einschnürenden Bewehrung.

In den folgenden Abschnitten werden die verschiedenen bestehenden Ansätze zur Bestimmung der maßgebenden Umschließungsfläche A_conf (und des entsprechenden Wirksamkeitsfaktors k) nach den aktuellen Bemessungsrichtlinien (EC 2, SIA 262 und MC 2010) und nach einem in [1] vorgestellten neuen Modellansatz für passive Umschnürung vorgestellt.

Bemessungsansätze nach Bemessungsrichtlinien

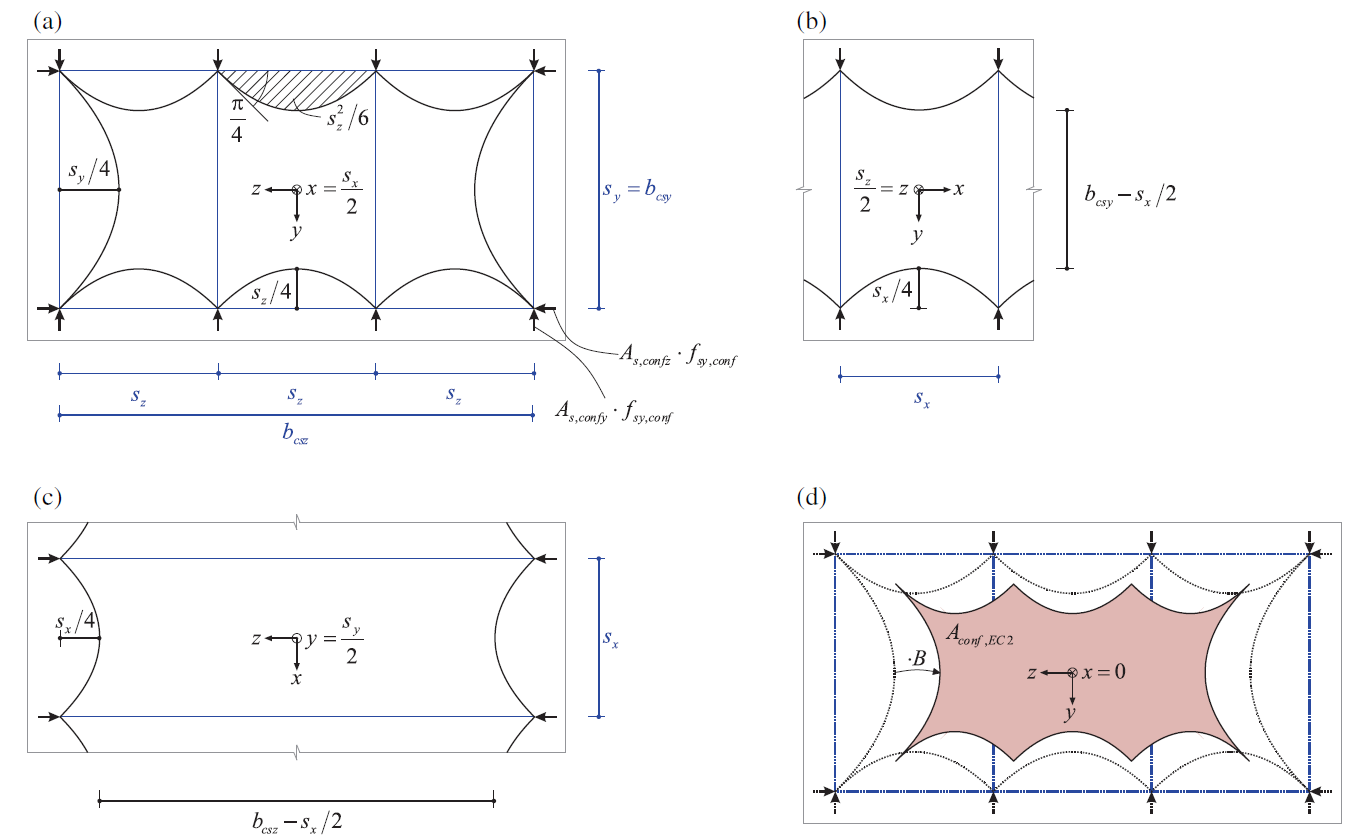
EC2 ermittelt die maßgebende Umschnürungsbetonfläche A_conf,EC2 aus der Wölbungswirkung zwischen den diskret verteilten Lasteinleitungspunkten der Umschließungsbewehrung.

\[A_{conf.EC2}=\underset{A}{\underbrace{\left( b_{csy}\cdot b_{csz}-\frac{\sum s^{2}_{i}}{6}\right)}}\cdot \underset{B}{\underbrace{\left( \frac{(b_{csy}\cdot s_{x}/2)\cdot(b_{csz}-s_{x}/2)}{b_{csy}\cdot b_{csz}}\right)}}\]

\[= \left( b_{csy}\cdot b_{csz}-\frac{\sum s^{2}_{i}}{6}\right) \cdot \left(1-\frac{s_{x}}{2\cdot b_{csy}} \right) \cdot \left(1-\frac{s_{x}}{2\cdot b_{csz}} \right)\]

Diese Gleichung, die für rechteckige Querschnitte gilt, basiert auf der Arbeit von Mander [2]. Weitere Informationen und ein Verständnis der Teile A und B finden Sie in [1].

\( \textsf{\textit{\footnotesize{Abb. 3\qquad Definition der Spannbetonfläche nach EC 2: (a) Spannbetonfläche im Schnitt einer Umschließung }}}\) \( \textsf{\textit{\footnotesize{Bewehrungsschicht (z. B. x = sx/2), (b) und (c) Längsausbreitung der Umschließungskräfte, (d) maßgebende Umschließungsbetonfläche }}}\) \( \textsf{\textit{\footnotesize{Fläche in der Mitte zwischen zwei einschnürenden Bewehrungslagen (z.B. x=0, gestrichelte Linien zeigen den Schnitt aus (a) als Referenz).}}}\)

Es ist erwähnenswert, dass in EC2 der Wirksamkeitsfaktor der Umschnürungsbewehrung k verwendet wird, um den Tragwiderstand auszudrücken. Der Faktor k ist das Verhältnis zwischen der maßgebenden Spannbetonfläche A_conf und der Querschnittsfläche A_c.

\[k=\frac{A_{conf}}{A_{c}}\]

Mit diesem Faktor kann der Tragwiderstand N_R wie folgt umgeschrieben werden:

\[N_{R}=\left( f_{c}+k\cdot \Delta f_{conf}\right)\cdot A_{c}+(f_{sy.l}-f_{c})\cdot A_{s.l}\]

Der effektive Faktor ist dann definiert als:

\[k=\left(\frac{b_{csy}\cdot b_{csz}-\frac{1}{6} \sum b_{i}^{2}}{b_{cy}\cdot b_{cz}}\right)\cdot \left(1-\frac{s_{x}}{2\cdot b_{csy}} \right)\cdot \left(1-\frac{s_{x}}{2\cdot b_{csz}} \right)\]

Für die Zwecke dieses Artikels halten wir uns jedoch an den Ausdruck für den Tragwiderstand N_R vom Anfang des Kapitels über die Verwendung der maßgebenden begrenzten Betonfläche A_conf.

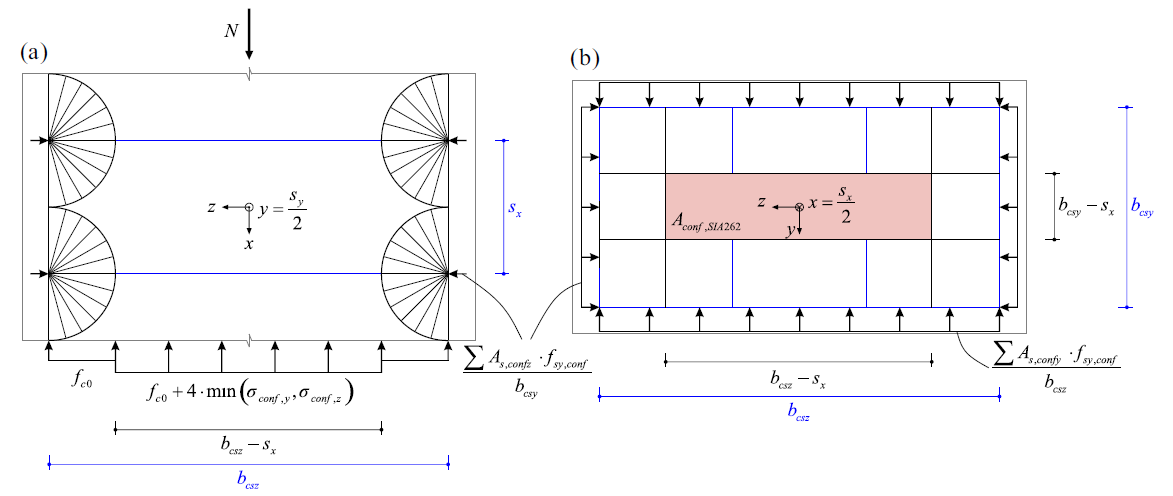
SIA 262 definiert die maßgebende Spannbetonfläche A_conf,SIA262 auf der Grundlage des in Abbildung 4 dargestellten Spannungsfeldes, das von Sigrist [7] vorgeschlagen wurde.

\[A_{conf.SIA262}=(b_{csy}-s_{x})\cdot (b_{csz}-s_{x})\]

\( \textsf{\textit{\footnotesize{Abb. 4\qquad Definition des Spannbetonbereichs nach SIA 262: (a) Spannungsfeld und (b) Seitenschnitt in der Ebene }}}\) \( \textsf{\textit{\footnotesize{der einschnürenden Bewehrung (z.B. x = sx/2).}}}\)

MC 2010 definiert den maßgebenden umgeschnürten Betonbereich als eine Kombination der beiden Modelle, die der Formulierung von EC 2 und SIA 262 zugrunde liegen:

\[A_{conf.MC2010}=\left( b_{csy}\cdot b_{csz}-\frac{\sum s^{2}_{i}}{6}\right)\cdot \left( \frac{(b_{csy}\cdot s_{x})\cdot(b_{csz}-s_{x})}{b_{csy}\cdot b_{csz}}\right)\]

\[= \left( b_{csy}\cdot b_{csz}-\frac{\sum s^{2}_{i}}{6}\right) \cdot \left(1-\frac{s_{x}}{b_{csy}} \right) \cdot \left(1-\frac{s_{x}}{b_{csz}} \right)\]

Der in [1] eingeführteneue Modellansatz für passive Umschnürung definiert die vereinfachte Umschließungsfläche A_conf,simp als Funktion der Geometrie und des Abstands der Umschließungsbewehrung.

\[A_{conf.simp}=\left(b_{csy}-\frac{\sqrt{s_{x}^{2}+s_{z}^{2}}}{2}\right)\cdot \left(b_{csz}-\frac{\sqrt{s_{x}^{2}+s_{y}^{2}}}{2}\right)\]

IDEA StatiCa Detailmodelle

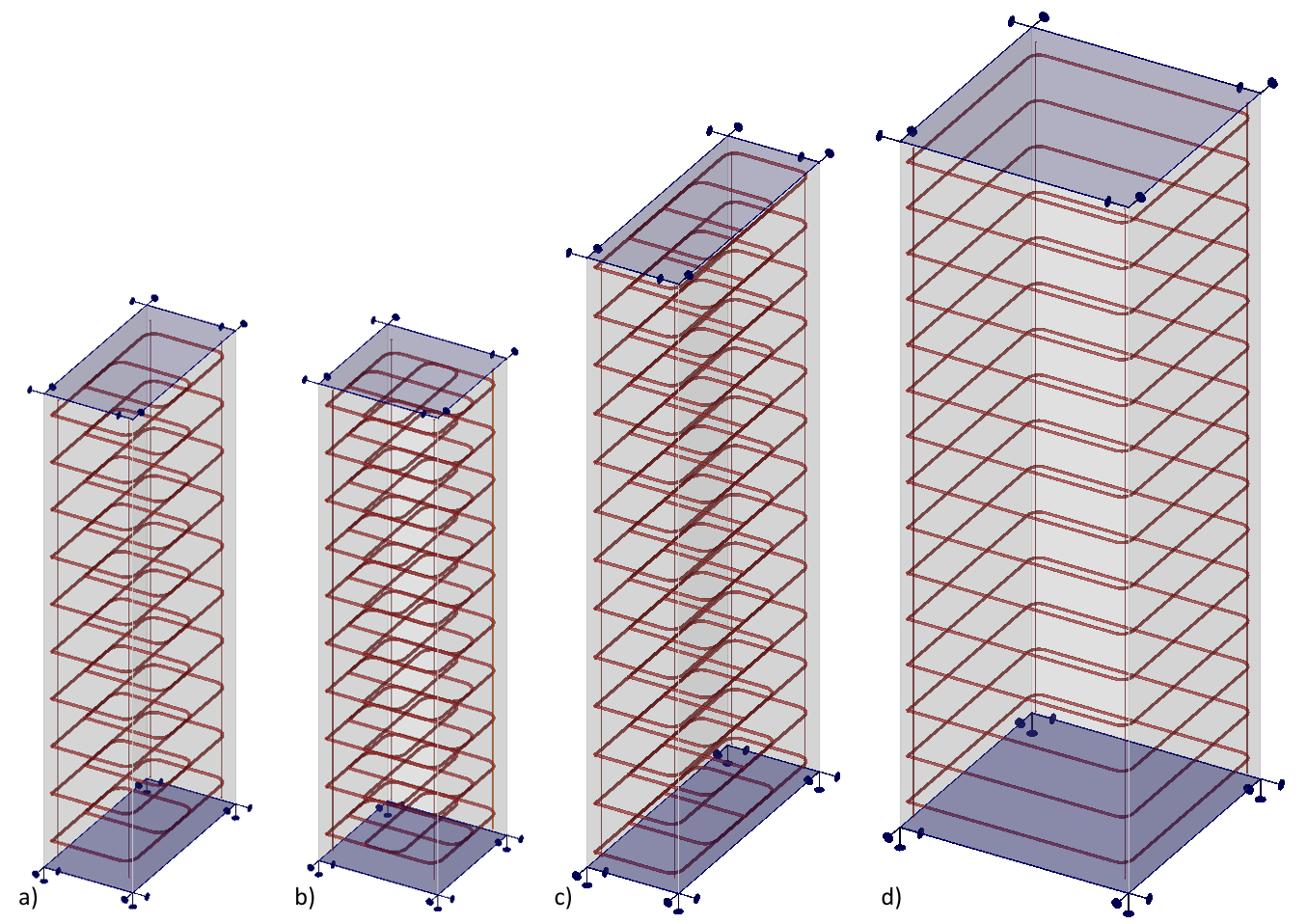
Bei den Modellen handelt es sich um Volumenmodelle mit unterschiedlichen Grundrissabmessungen b_cy x b_cz, Höhe h_x und Bügelabstand s_x aus Beton C30/37, die an der Unterseite in X-, Y- und Z-Richtung starr abgestützt sind. Um die Stabilität der oberen Betondecke im Modell zu gewährleisten, wird die obere Fläche auch in horizontaler Richtung starr abgestützt. Die Betondeckung c beträgt bei allen Modellen 30 mm. Es sind immer vier Längsbewehrungsstäbe mit dem Durchmesser Φ_s,l = 10 mm vorhanden. Die Bügel, die einschnürende Bewehrung und die Längsstäbe werden aus Stahl B500B modelliert. Alle Berechnungen erfolgen in charakteristischen Werten.

\[ \textsf{\textit{\footnotesize{Abb. 5\qquad IDEA StatiCa Detailmodelle a) 0,75 x 1,5 x 4,0; b) 1,0 x 1,0 x 4,0; c) 0,75 x 2,5 x 5,0; d) 2,0 x 2,0 x 6,0}}}\]

Es wird immer eine Last aufgebracht, die größer ist als die erwartete Tragfähigkeit. Das Programm sucht dann nach der maximal möglichen anwendbaren Last, damit eines der definierten Kriterien nicht überschritten wird. In diesem Fall ist es immer das Grenzdehnungskriterium der Bügelbewehrung, das bei maximal 5% liegt, aber aufgrund der implementierten Zugaussteifung ist der Grenzwert in der Regel niedriger. Für weitere Details siehe Theoretischer Hintergrund.

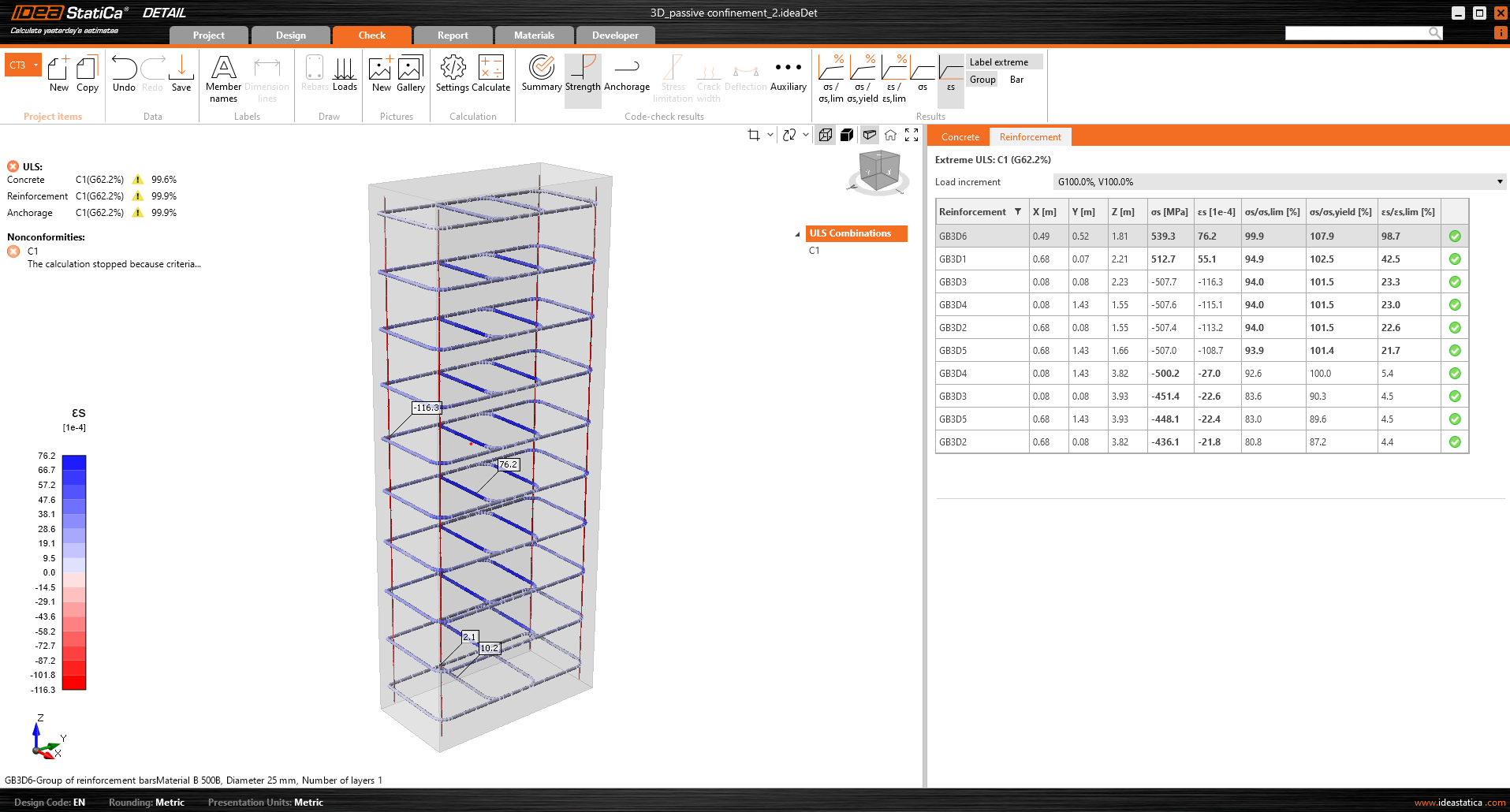
In der folgenden Abbildung ist zu sehen, dass die Berechnung des Modells 0,75 x 1,5 x 4,0 abgebrochen wurde und ein Vielfaches der aufgebrachten Last als maximale Last, die das Element aushalten kann, ermittelt wurde.

\[ \textsf{\textit{\footnotesize{Abb. 6\qquad IDEA StatiCa Detail - Grenzdehnung in der Bewehrung}}}\]

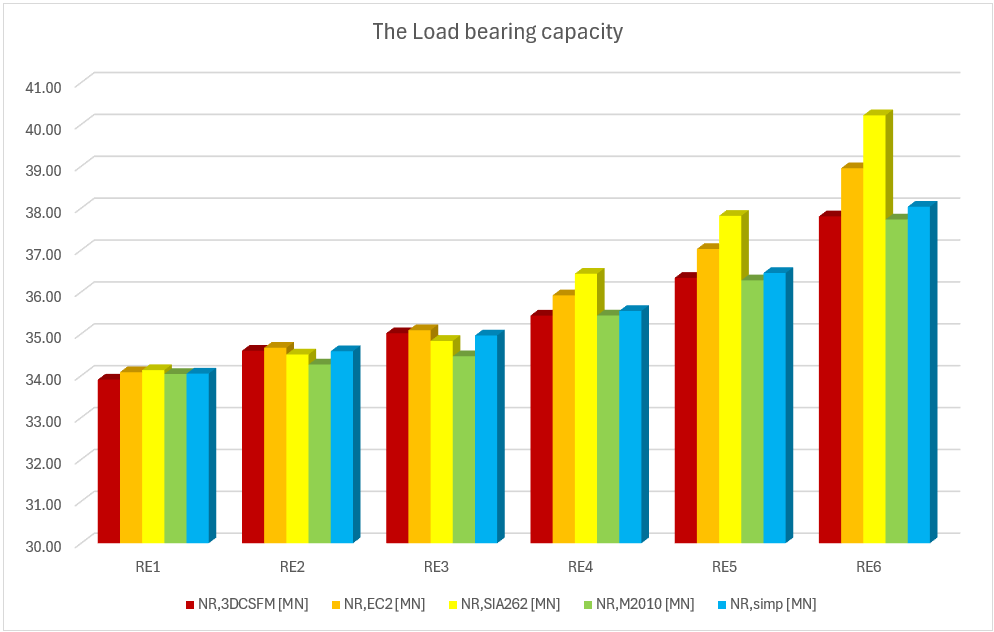
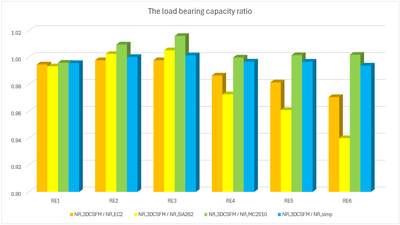
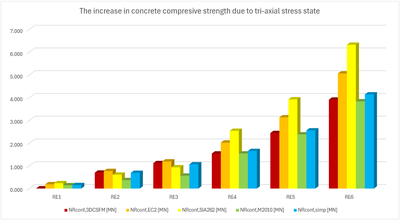
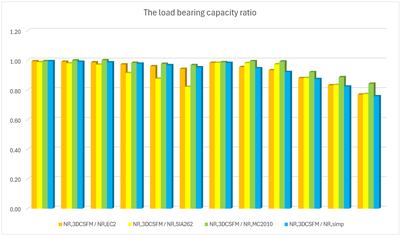
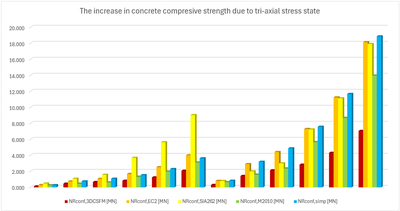
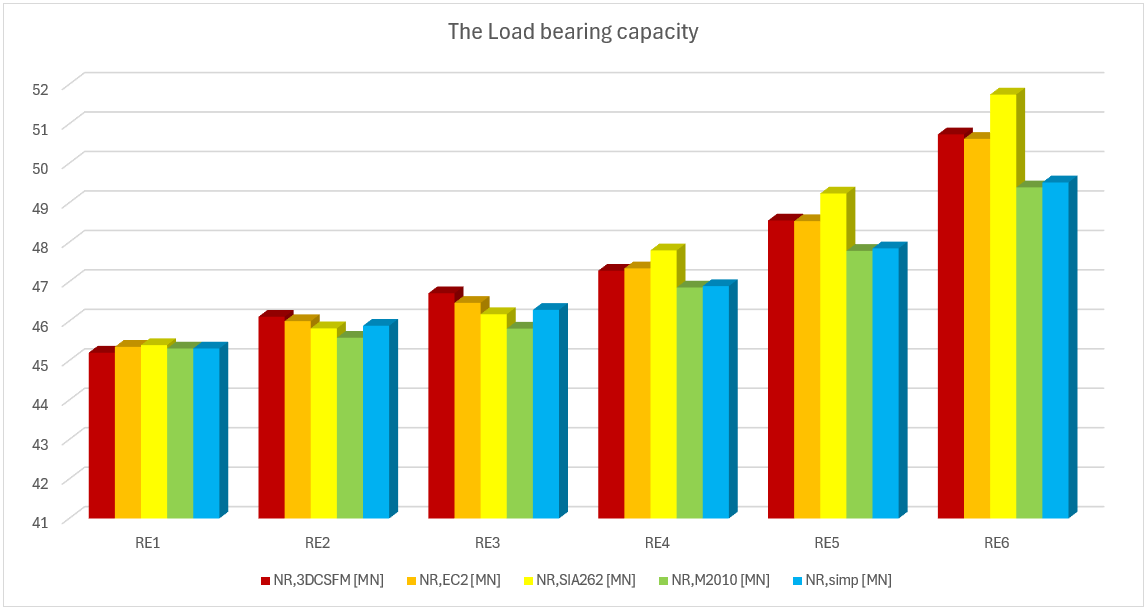
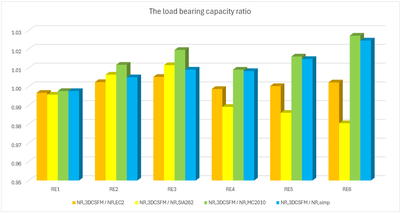
Vergleich der einzelnen Modelle

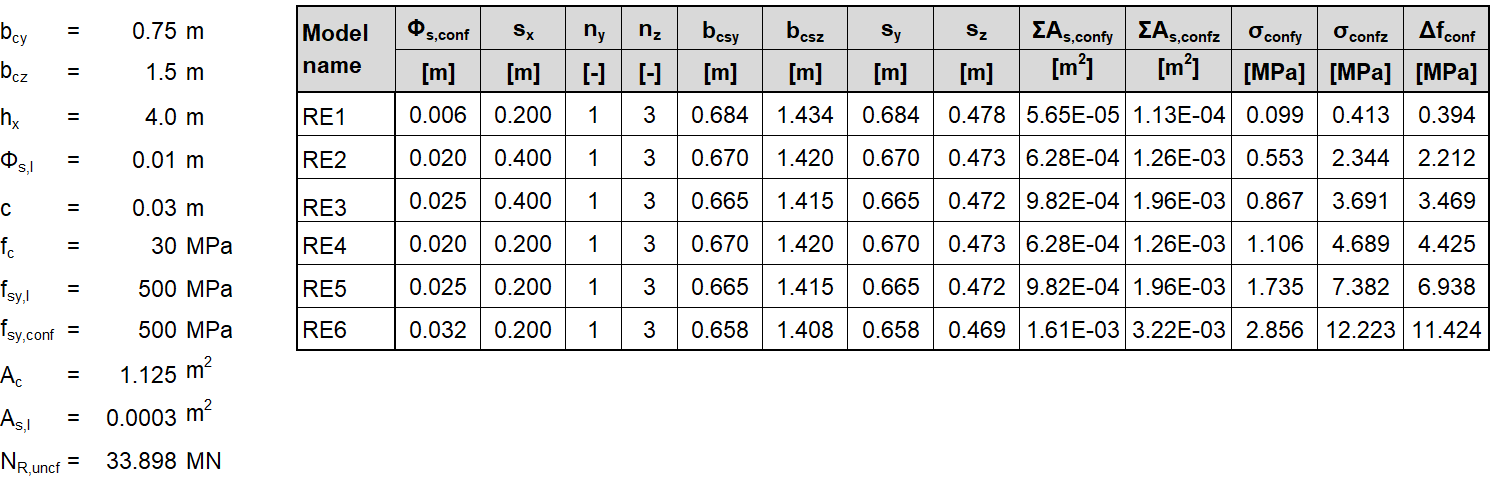
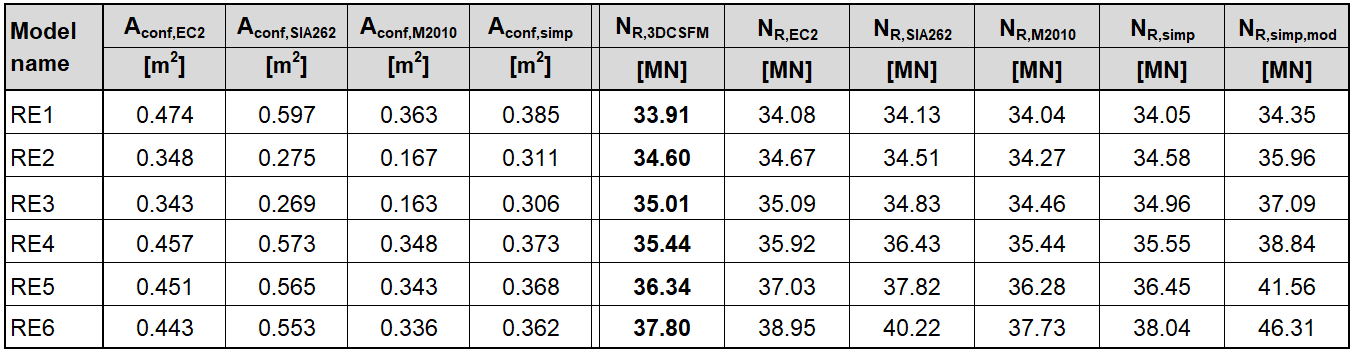
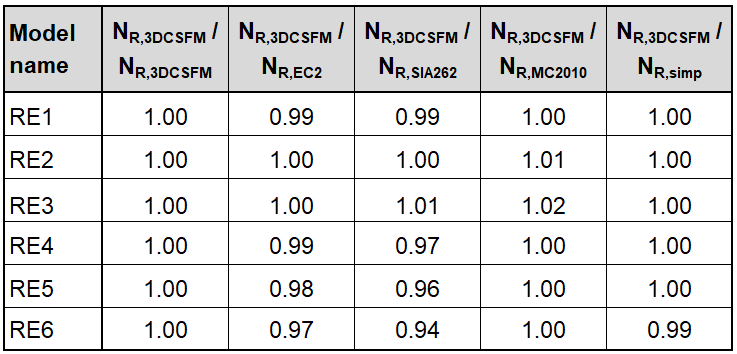
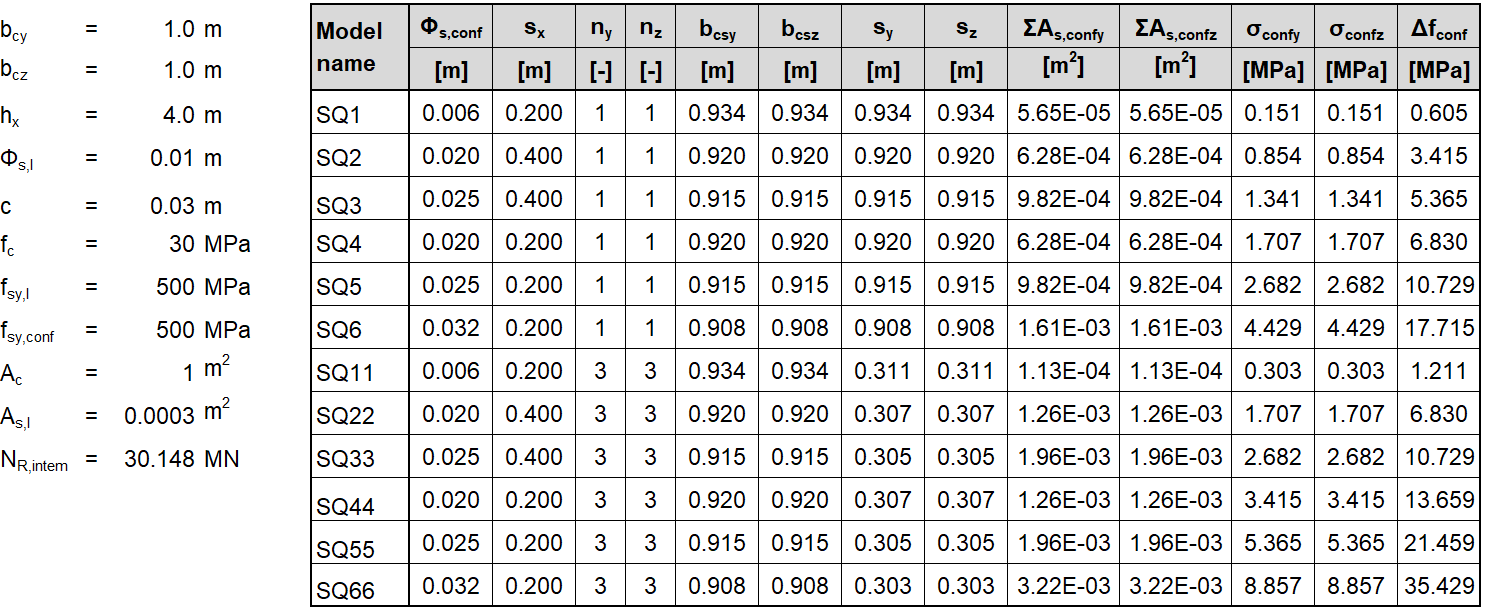
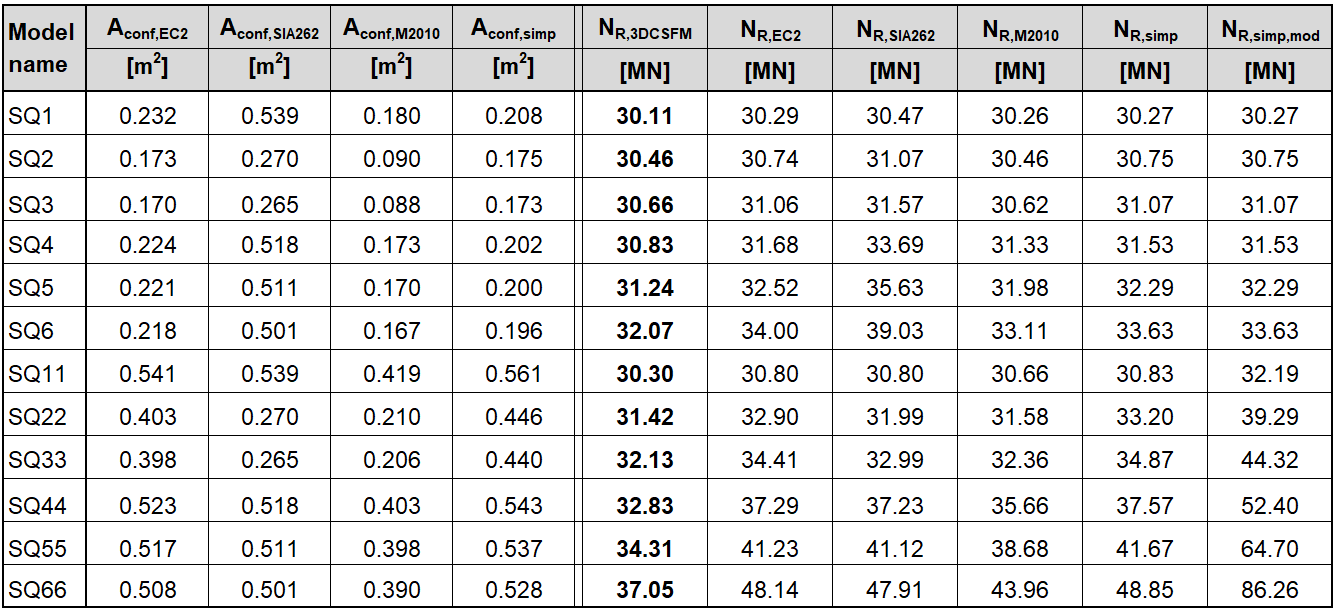
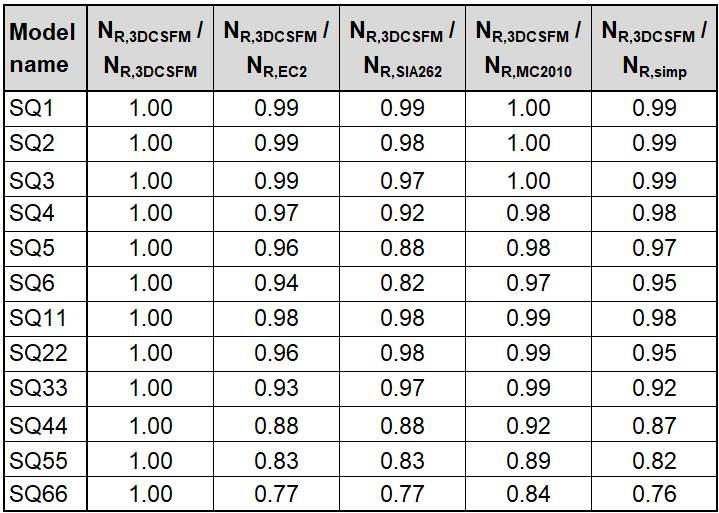
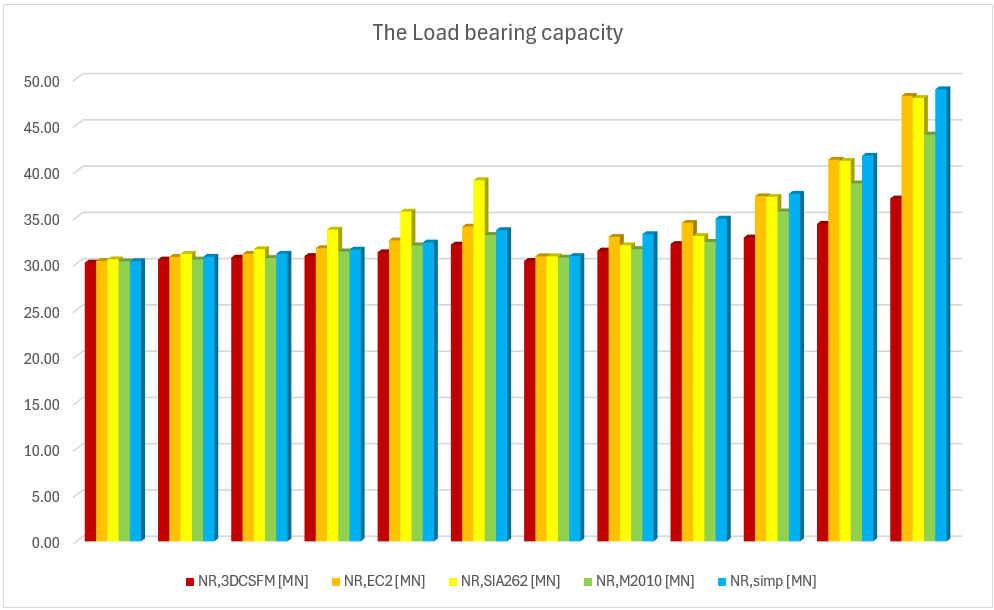
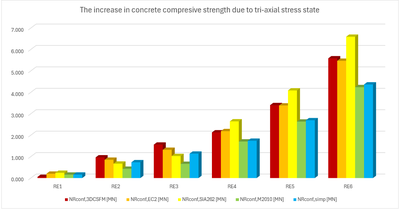
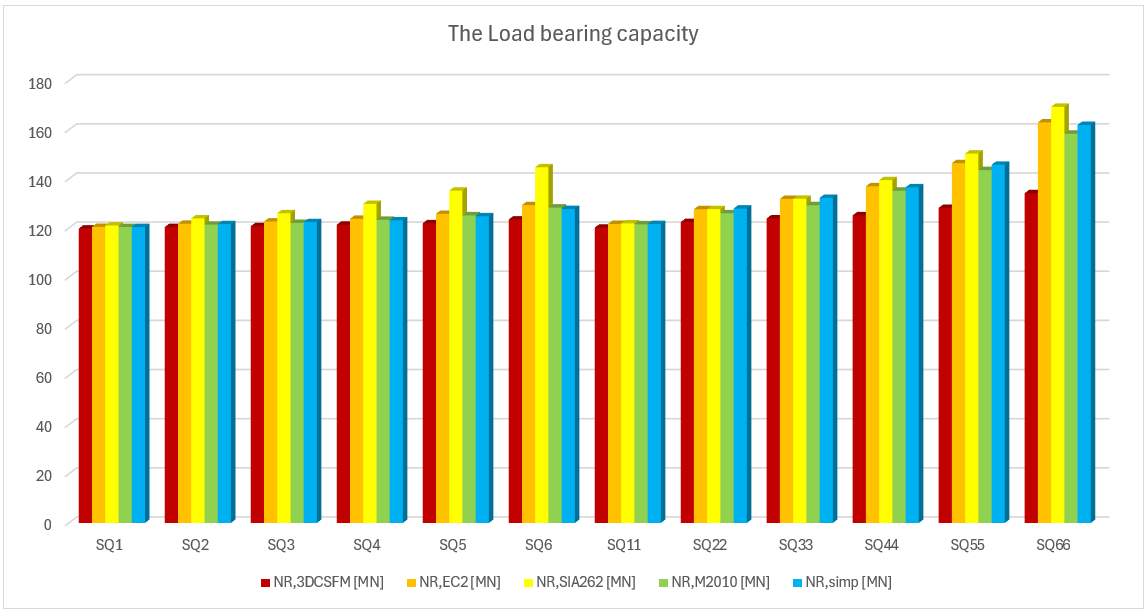
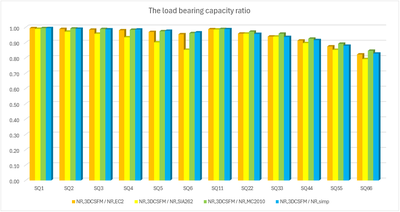
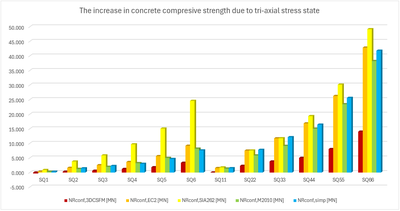
In den folgenden Tabellen und Grafiken werden alle in der Anwendung IDEA StatiCa Detail erstellten Modelle mit den analytischen Ansätzen verglichen, einschließlich aller Zwischenergebnisse für ein rechteckiges und ein quadratisches Modell. Allerdings gibt es Hilfsvariablen, die zunächst definiert werden müssen.

Φ_s,l und Φ_s,conf sind die Durchmesser der Längs- und Umschnürungsbewehrung, n_y und n_z sind die Anzahl der Zwischenräume s_y und s_z (was bedeutet, dass die Anzahl der Bügelschenkel n+1 ist), N_R,uncf und N_R,conf sind wie folgt definiert:

\[N_{R,uncf}=f_{c}\cdot A_{c}+(f_{sy.l}-f_{c})\cdot A_{s.l}; N_{R,conf}=\Delta f_{conf}\cdot A_{conf}\]

Rechteckiges Modell a) 0,75 x 1,5 x 4,0

Quadratisches Modell b) 1,0 x 1,0 x 4,0

Rechteckiges Modell c) 0,75 x 2,5 x 5,0

Quadratisches Modell d) 2,0 x 2,0 x 6,0

Schlussfolgerung

Aus den oben dargestellten Ergebnissen können mehrere Schlussfolgerungen gezogen werden. Im Allgemeinen haben sich die 3D-CSFM-Ergebnisse als recht konservativ erwiesen, insbesondere bei quadratischen Modellen, bei denen der Anstieg der Tragfähigkeit aufgrund der Einschließung in einigen Beispielen weniger als die Hälfte beträgt. Für rechteckige Modelle ist eine gute Übereinstimmung innerhalb von 2 % Abweichung zu beobachten. Von den untersuchten analytischen Methoden zeigt der EC2-Ansatz bei allen Modellen die beste Übereinstimmung. Diese Überprüfung zeigt, dass die Verwendung von 3D-CSFM unter dem Gesichtspunkt des passiven Einschlusses sicher ist und mit den etablierten Methoden der Normen übereinstimmt.

Referenzen

[1] MORGER, Fabian; KENEL, Albin und KAUFMANN, Walter. Passive Umschließung von Stahlbetonbauteilen revisited. Online. Structural Concrete. ISSN 1464-4177. https://doi.org/10.1002/suco.202400209.

[2] Mander JB, Priestley MJN, Park R. Observed stress-strain behavior of confined concrete. J Struct Eng. 1988;114:1827–49. https://doi.org/10.1061/(ASCE)0733-9445(1988)114:8(1827)

[3] Internationaler Verband für Baubeton (fib). Model code for concrete structures 2010; 2013.

[4] SIA. Swisscode SIA 262: Betonbauwerke. Zürich, Schweiz: Schweizerischer Ingenieur- und Architektenverein (SIA); 2013.

[5] EN 1992-1-1:2023. Eurocode 2 - Bemessung und Konstruktion von Betontragwerken - Teil 1-1: Allgemeine Regeln und Regeln für Gebäude, Brücken und Ingenieurbauwerke; 2023.

[6] Nielsen MP, Hoang LC. Grenzwertanalyse und Betonplastizität. 3rd ed. Boca Raton, FL: CRC Press; 2011. https://doi.org/10.1201/b10432

[7] Sigrist V. Zum Verformungsvermögen von Stahlbetonträgern [On the deformation capacity of structural concrete girders]. Dissertation. ETH Zürich; 1995. https://doi.org/10.3929/ethz-a-001492371