Schubversuche an Balken mit geringen Bügelmengen
Einführung
Im folgenden Artikel wollen wir das Schuversagen in Trägern mit geringen Bügelmengen untersuchen. Wir werden experimentelle Daten mit dem 3D-CSFM Solid Block Modell vergleichen, um das Last-Verformungs-Verhalten zu analysieren und Versagensarten vorherzusagen. Dieser Test umfasst drei Beispiele, die sich in der Bewehrungsmenge und den Abmessungen des Trägers unterscheiden. Darüber hinaus erweitert dieser Artikel die bestehende Überprüfung des 2D-CSFM[1], indem er eine detailliertere Untersuchung der Netzvariationen bietet. Alle CSFM-basierten Methoden wurden in der IDEA StatiCa Detail-Anwendung unter Verwendung der meisten Standardeinstellungen durchgeführt. Weitere Erkenntnisse zu diesem Thema werden später in diesem Artikel diskutiert.
Definition der Versagensarten
Um den Vergleich der in den Versuchen beobachteten Versagensarten mit den von der CSFM vorhergesagten zu erleichtern, werden die Versagensarten entweder als Biegeversagen (F) oder als Schubversagen (S) kategorisiert. Obwohl das Fließen der Bewehrung an sich kein Materialversagen darstellt, wird es als Teil der Klassifizierung der Versagensarten in Verbindung mit dem Bruch des Betons berücksichtigt.
\[ \textsf{\textit{\footnotesize{Tabelle 1.1\qquad Definition der Versagensarten}}}\]
Aufbau der Versuche
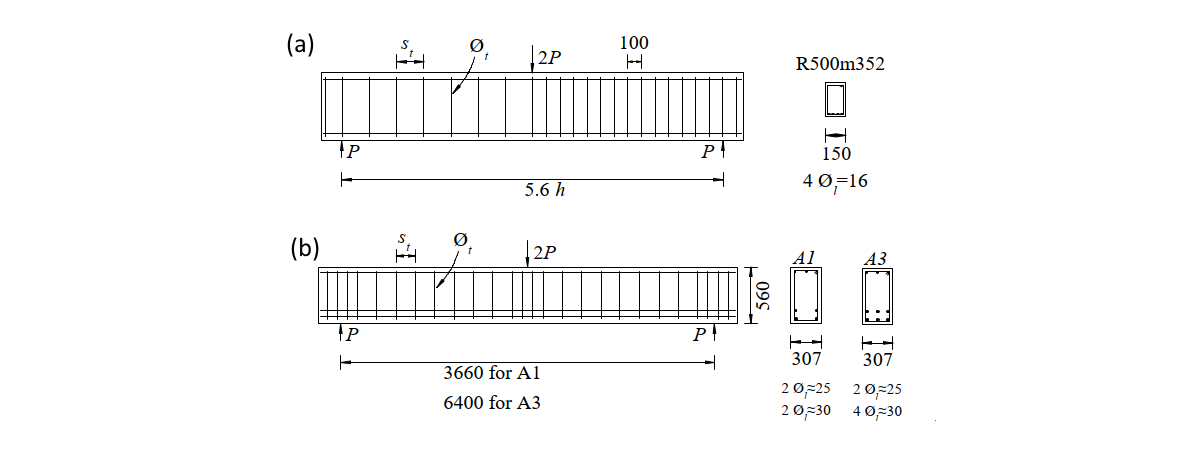
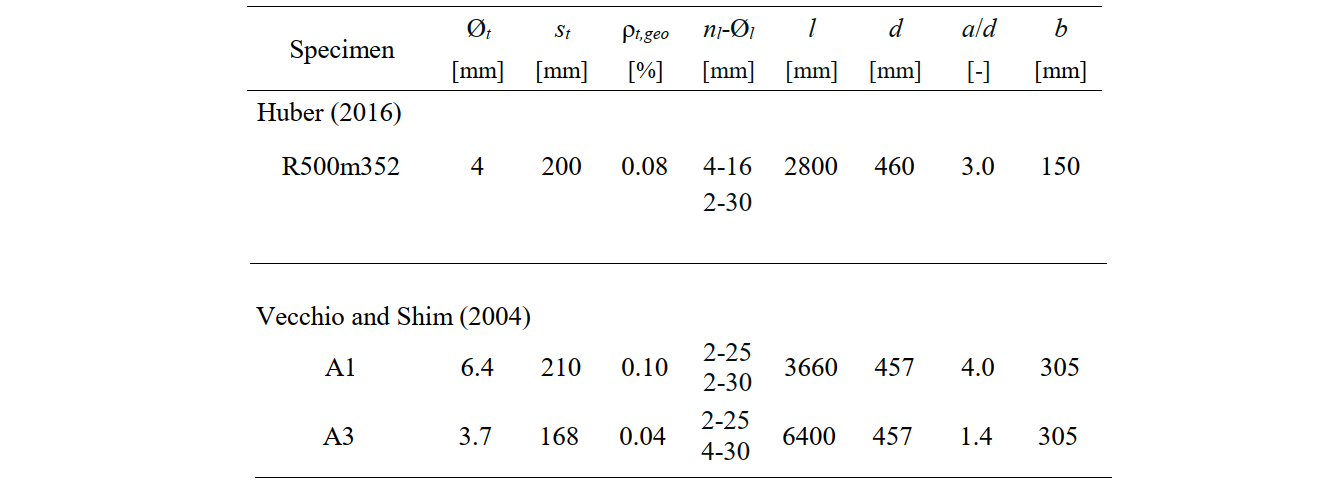
In diesem Einzelversuch handelt es sich um ein Einfeldsystem, das mit einer Einzelkraft in der Mitte der Spannweite belastet ist. Die Parameter für die Bewehrung des Trägers sind in Abb. 2.1 zusammengefasst. Diese Tabelle enthält Informationen wie den Durchmesser der Querkraftbewehrung (Øt), den Abstand (st) und den geometrischen Bewehrungsgrad (ρt,geo). Darüber hinaus werden Angaben zur Biegebewehrung, einschließlich der Anzahl (nl) und des Durchmessers (Øl) der Stäbe, sowie zur Geometrie der Balken mit der effektiven Höhe (d), dem Schubschlankheitsverhältnis (a/d) und der Breite (b) gemacht. Bei dem von Huber 2016[3] durchgeführten Versuch mit der Bezeichnung R 500m352 wurden Einzelbewehrungsstäbe verwendet. Im Gegensatz dazu wurden bei den Probekörpern A1 und A3, die Teil eines von Vecchio und Shim im Jahr 2004[2] durchgeführten Versuchs waren, geschlossene Bügel mit zwei Schenkel verwendet.
\[ \textsf{\textit{\footnotesize{Abb. 2.1\qquad Abmessungen und Art der Bewehrung: (a) R500m352, (b) A1, A3 }}}\]
\[ \textsf{\textit{\footnotesize{Tabelle 1.2\qquad Verstärkungseigenschaften}}}\]
Materialeigenschaften
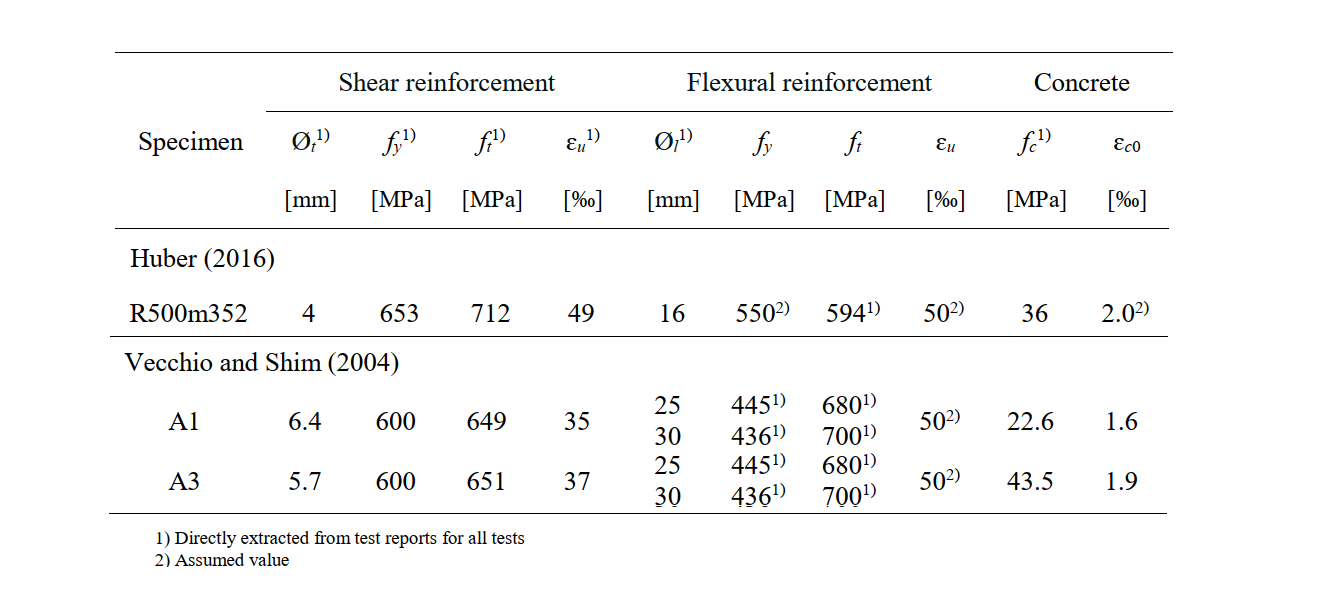
Die Materialeigenschaften des Betons, der Bewehrung und der Anker, die in der CSFM-Analyse verwendet werden, sind in Tabelle 1.3 aufgeführt. Die meisten der für die Eingabe in das CSFM erforderlichen Materialeigenschaften wurden in den Berichten der jeweiligen Versuche angegeben. Werte, die nicht explizit angegeben wurden und daher angenommen wurden, sind in der Tabelle markiert.
\[ \textsf{\textit{\footnotesize{Tabelle 1.3\qquad Materialeigenschaften}}}\]
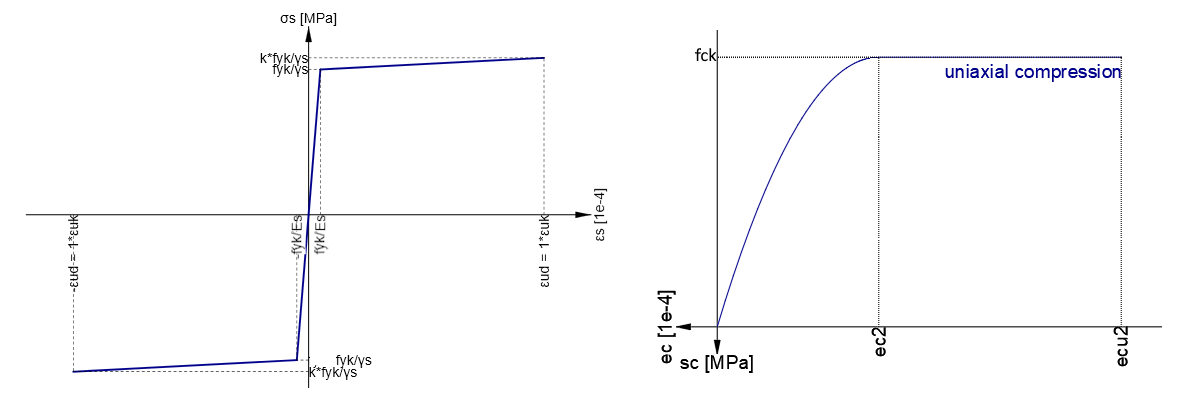
\[ \textsf{\textit{\footnotesize{Abb. 2.2\qquad Spannungs-Dehnungs-Diagramme der Materialien: (a) Spannungs-Dehnungs-Diagramm der Bewehrung,}}}\] \[ \textsf{\textit{\footnotesize{(b) Spannungs-Dehnungs-Diagramm des Betons}}}\]
Modellierung mit 3D-CSFM
Die in den 2D- und 3D-CSFM-Analysen verwendeten Material- und Bewehrungsparameter wurden aus Tabelle 1.2 bzw. Tabelle 1.3 entnommen. In der 3D-CSFM wurden die Balken mit der Solid-Block-Modellklasse in IDEA StatiCa Detail modelliert. Die Belastung der Träger wurde in der Mitte der Spannweite als Flächenlast über eine Fläche von 0,2 m mal b (Breite des Trägers) aufgebracht, wobei die resultierende Kraft in Übereinstimmung mit den experimentellen Daten wirkte. Die Auflagerbedingungen für die Balken wurden als einfach gestützt modelliert, wobei eine 0,15 m x 0,30 m große Flächenstütze verwendet wurde. Diese Konfiguration wurde entwickelt, um die experimentellen Aufbaubedingungen genau nachzubilden und eine realistische Simulation des Balkenverhaltens unter Last zu ermöglichen.
Alle Teilfaktoren in IDEA StatiCa Detail sind auf den Wert 1.0 eingestellt.
\[ \textsf{\textit{\footnotesize{Abb. 2.3\qquad Lasten in IDEA StatiCa Detail: (a) 3D-CSFM: A1 - Vecchio und Shim (2004), (b) 2D-CSFM: R500m352 - Huber (2016)}}}\]
Last-Verformungs-Kurve
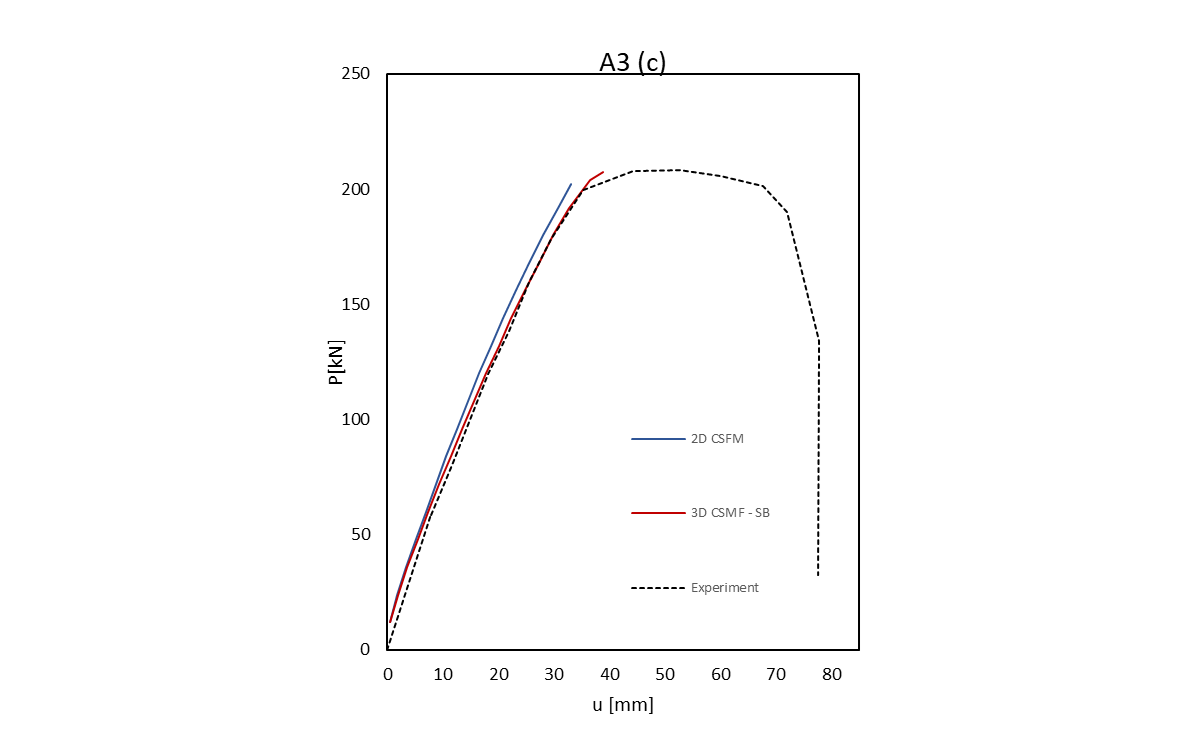
Der Vergleich zwischen den numerischen Methoden und den experimentellen Daten kann in Abbildung 2.4 veranschaulicht werden. In dieser Abbildung sind die experimentellen Daten durch eine schwarze gestrichelte Linie dargestellt, während das 2D-CSFM mit einer blauen durchgezogenen Linie und das 3D-CSFM mit einer roten durchgezogenen Linie abgebildet ist. Die Diagramme zeigen eine starke Korrelation zwischen den numerischen Methoden und den experimentellen Daten, was darauf hindeutet, dass die Simulationen das in den physikalischen Experimenten beobachtete Verhalten effektiv abbilden.
\[ \textsf{\textit{\footnotesize{Abb. 2.4\qquad Last-Verformungs-Reaktionen: (a) R500m352, (b) A1, (c) A3}}}\]
Der Vergleich der kritischen Last ist aus Abbildung 2.5 und der prozentualen Nachgiebigkeit aus Tabelle 1.4 ersichtlich. Für alle Beispiele ergibt sich eine konsistente Übereinstimmung mit den experimentellen Ergebnissen.
\[ \textsf{\textit{\footnotesize{Abb. 2.5\qquad Kritische Last: (a) R500m352, (b) A1, (c) A3}}}\]
\[ \textsf{\textit{\footnotesize{Tabelle 1.4\qquad Kritische Last im Vergleich}}}\]
\[ \textsf{\textit{\footnotesize{Tabelle 1.5\qquad Kritische Belastung und Vergleich der Ausfallarten}}}\]
Fazit
Im Rahmen des Einheitstests wird ein Vergleich zwischen dem experimentellen Verhalten und den CSFM-Simulationen, sowohl in 2D als auch in 3D, eines Trägers mit einer geringen Bewehrung durchgeführt. Zu den wichtigsten Erkenntnissen des Artikels gehören:
- Sowohl die 2D- als auch die 3D-CSFM-Simulationen stimmen gut mit den experimentellen Daten überein und zeigen, dass sie in der Lage sind, das Tragverhalten von Trägern mit minimaler Bewehrung genau vorherzusagen.
- Die Verwendung der 3D-Volumenblockmodellierung und der äquivalenten 2D-Modellierungstechniken ist wirksam bei der Darstellung der tatsächlichen Bedingungen der Träger unter Last, was durch die starke Korrelation mit den experimentellen Ergebnissen bestätigt wird.
- Die Ergebnisse des Last-Verformungs-Verhaltens, des Vergleichs der kritischen Last und der Vorhersage des Versagensmodus zeigen eine ausreichende Übereinstimmung mit den experimentellen Resultaten. Diese gute Übereinstimmung unterstreicht die Wirksamkeit und Genauigkeit der CSFM-Simulationen bei der Modellierung des tatsächlichen Verhaltens von Trägern unter verschiedenen Belastungsbedingungen.
\[ \textsf{\textit{\footnotesize{Abb. 2.6\qquad Spannungsfeldergebnisse R500m352}}}\]
Referenzen
[1] - Kaufmann, W., J. Mata-Falcón, M. Weber, T. Galkovski, D. Thong Tran, J. Kabelac, M. Konecny, J. Navratil, M. Cihal, and P. Komarkova. 2020. "Compatible Stress Field Design Of Structural Concrete". Berlin, Deutschland. "AZ Druck und Datentechnik GmbH, ISBN 978-3-906916-95-8.
[2] - Vecchio, F.J., und W. Shim. 2004. "Experimental and Analytical Reexamination of Classic Concrete Beam Tests". Journal of Structural Engineering 130 (3): 460-69.
[3] - Huber, P. 2016. "Beurteilung der Querkrafttragfähigkeit bestehender Stahlbeton- und Spannbetonbrücken." Dissertation, Wien: TU Wien, Fakultät für Bauingenieurwesen.