Auszugsverhalten von Ankerbolzen mit unterschiedlichen Verankerungstiefen
Einführung
Die Tragfähigkeit von in Beton eingegossenen Ankern hängt von vielen Faktoren ab. Die Festigkeit des Betons und des Ankermaterials sowie der Verbund zwischen Dübel und Beton sind entscheidende Materialparameter, die das Verhalten des Ankers bestimmen. Ein weiterer Faktor, der nicht weniger wichtig ist, ist die Geometrie des Ankers (und möglicherweise des gesamten Fundamentblocks). Die Länge des Ankers und das Vorhandensein anderer Bewehrung spielt ebenfalls eine wichtige Rolle für die Leistungsfähigkeit des Ankers.
Ziel dieses Artikels ist es, die auf dem CFSM basierende Berechnung zu überprüfen und zu validieren. Für die Validierung werden verschiedene Ankerlängen gemäß den verfügbaren Literaturdaten [1] ausgewählt. Die Verifizierung des vorgestellten Ansatzes basiert auf (I) dem Vergleich mit anderer etablierter Software für numerische Simulationen des Materialverhaltens und (II) der Übereinstimmung mit Standard-Bemessungsregeln.
Beschreibung des Versuchs
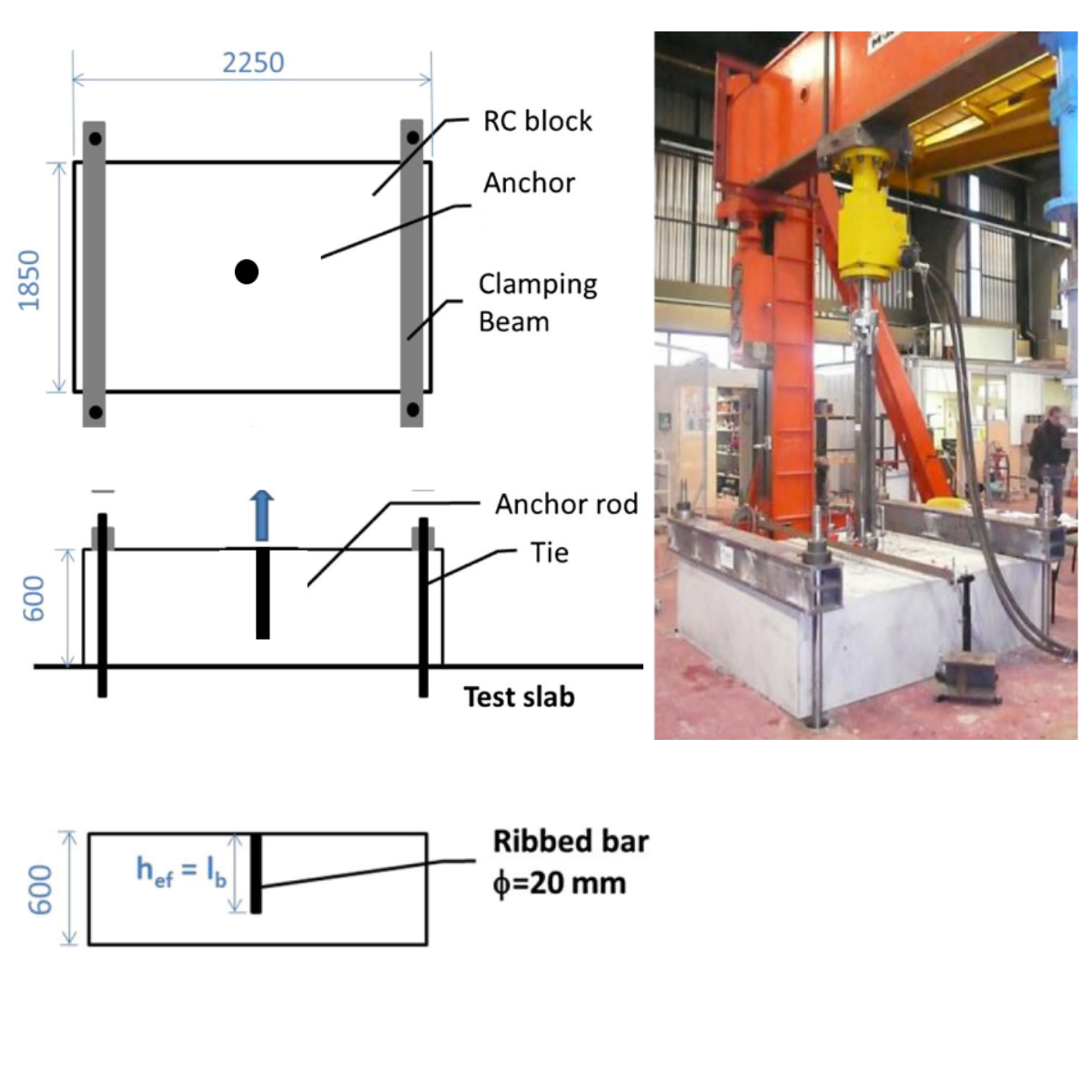
Bei der Versuchskampagne [1] werden in einem Betonblock Anker in voller Größe getestet. Die Stäbe bestehen aus Rippenstahl (FeE500B) und haben einen Durchmesser von 20 mm. Der Rippenstab hat eine Streckgrenze von 585 MPa, eine Bruchfestigkeit von 700 MPa, eine Bruchdehnung von 16 % und einen Elastizitätsmodul von 210 GPa. Drei verschiedene Tiefen (100, 150, 200 mm) werden getestet, um den Verbund, den Betonkonus oder das Versagen des Stabes zu beobachten. Die Anker sind in einen Stahlbetonblock (2250x1850x600 mm) eingegossen.
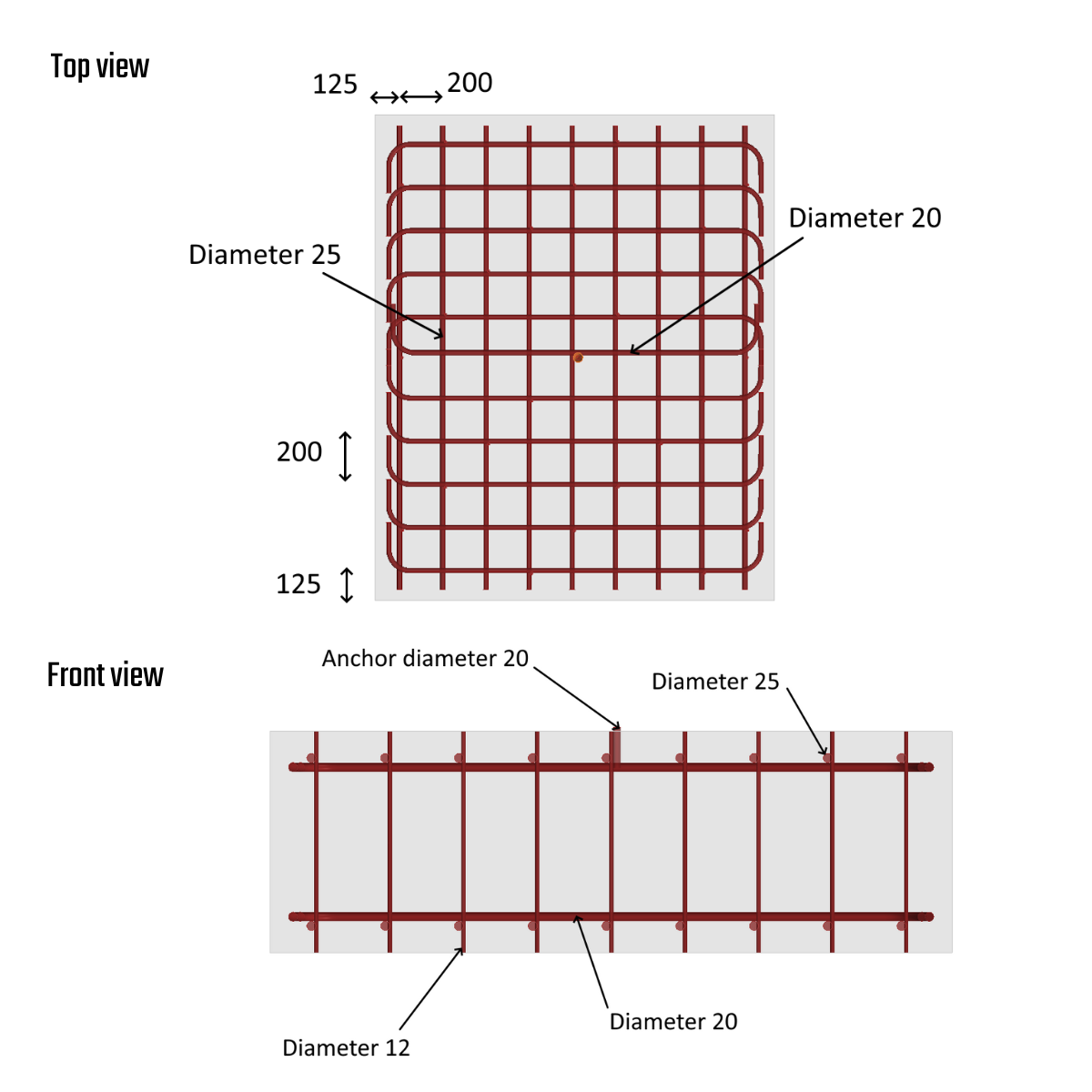
Zusätzlich werden einige Bügel mit einem Durchmesser von 12 mm eingebaut, um die beiden Bewehrungslagen zu stützen. Der Bewehrungsgrad beträgt 0,64 %. Die verwendete Betongüte ist C40/50. Der Betonblock wird durch zwei Metallprofile gesichert, die mit vier Spannstäben mit der Prüfplatte verbunden sind. Um die Verankerung herum wird kein einschränkender Druck ausgeübt. Der Hydraulikzylinder ist mit zwei symmetrischen Stangen an der Verankerung befestigt. Die quasi-statische Zugbelastung erfolgt weggesteuert mit einer Belastungsrate von 1 mm/min, und die Last wird bis zum Versagen des Dübels aufgebracht.
1) Ausziehversuchsaufbau - aus dem Artikel: Ausziehverhalten von eingegossenen Kopfankern und Verbundankern mit unterschiedlichen Verankerungstiefen - Fabien Delhomme, Thierry Roure ,Benjamin Arrieta, Ali Limam
2) Bewehrung und Ankeranordnung
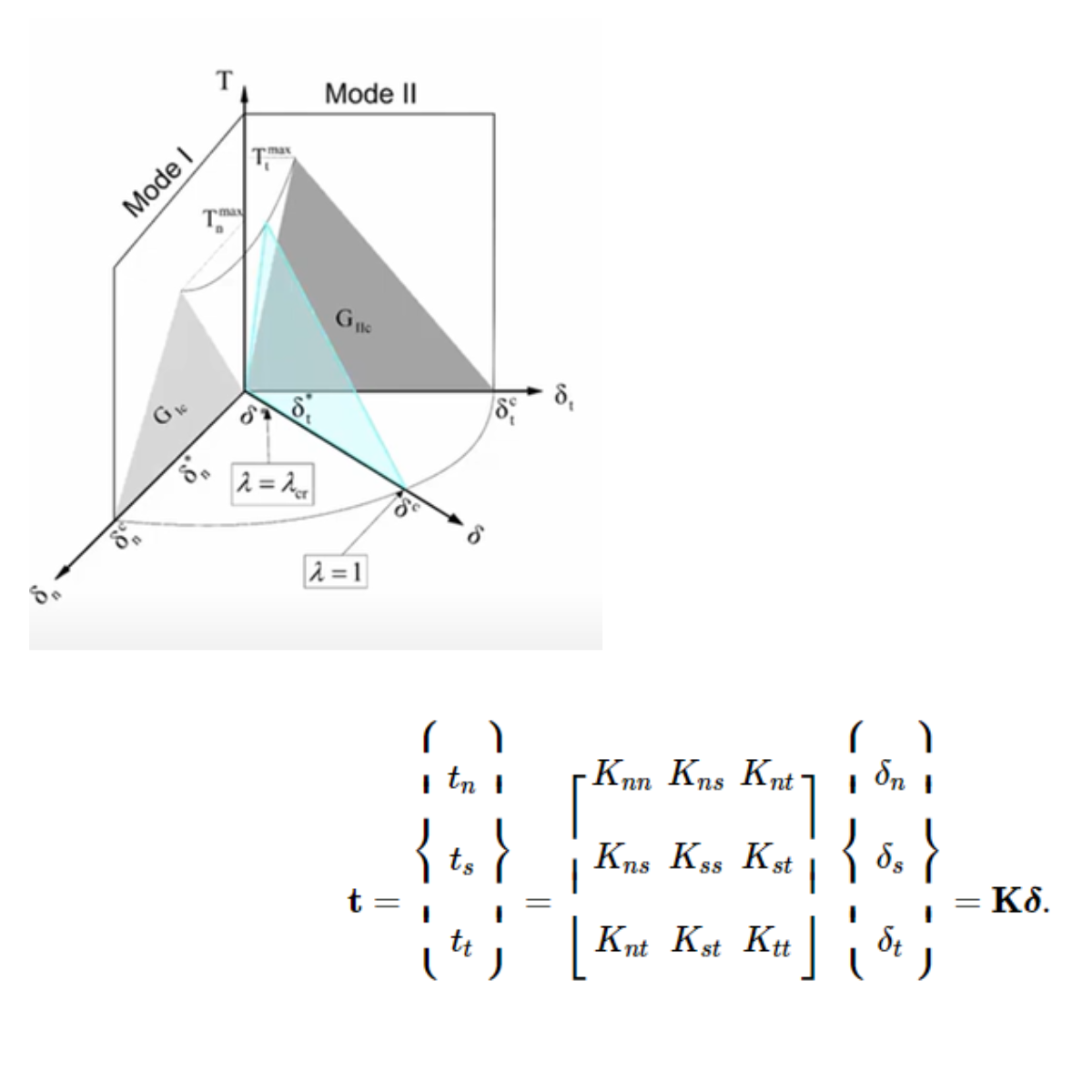
3D CSFM - Kompatible Spannungsfeldmethode
Theorie
3D CSFM definiert das Betonverhalten auf der Grundlage der Mohr-Coulomb-Plastizitätstheorie für monotone Belastung. Die Methode untersucht das Betonverhalten in Bezug auf die Hauptspannungen und vernachlässigt dabei die Betonzugfestigkeit. Die Auswirkung der Betonspannung wird nur bei der Zugaussteifung von Stahlstäben berücksichtigt.
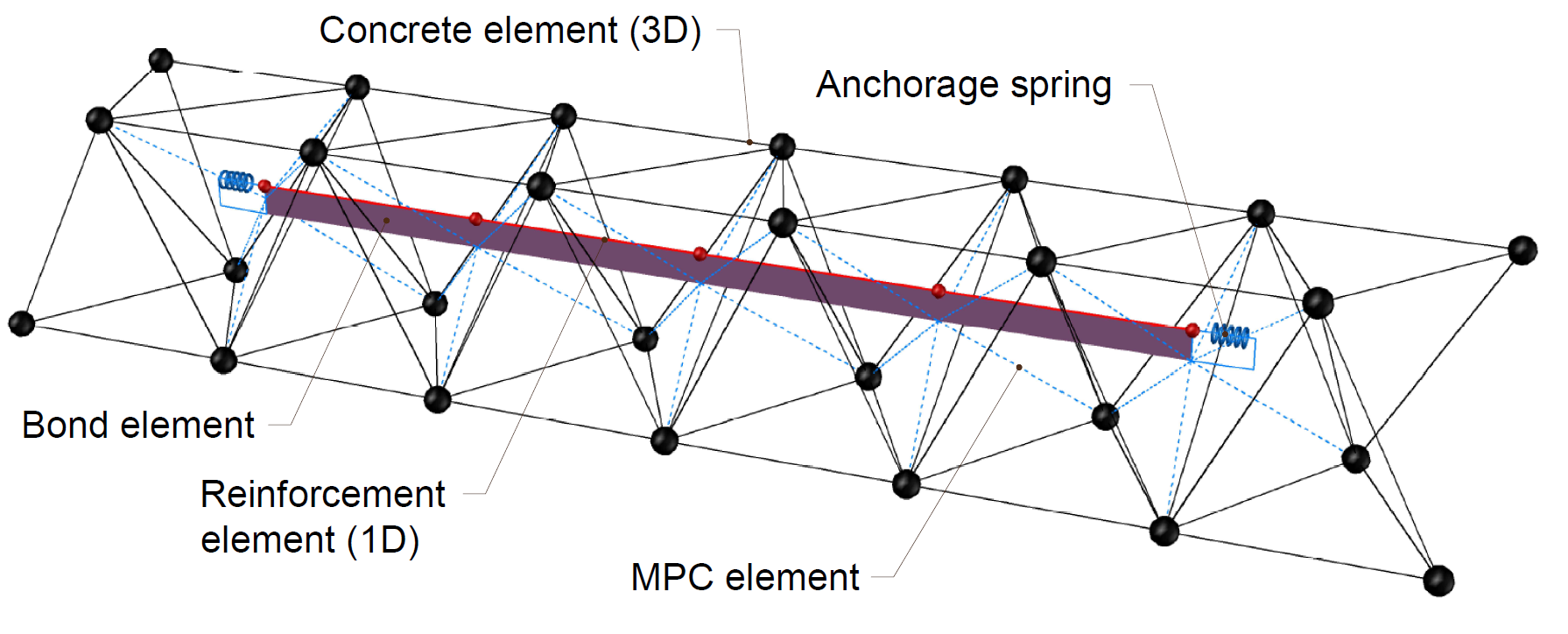
Die Bewehrungsstäbe sind mit den finiten Elementen des Betonvolumens durch Verbundelemente verbunden, die ein Gleiten zwischen Beton und Bewehrung ermöglichen. Es ist zu beachten, dass 3D CSFM nicht für die Simulation von unbewehrtem Beton geeignet ist, da es keine Zugspannung gibt, was zu irreführenden Verformungen und Modelldivergenzen führen kann.
Im Allgemeinen umfasst die Mohr-Coulomb-Theorie zwei grundlegende Eigenschaften, die die Entwicklung der Plastizitätsfläche unter Druck und teilweise unter Zug bestimmen: den inneren Reibungswinkel φ und den Kohäsionsparameter c. 3D CSFM geht von einem inneren Reibungswinkel von Null aus, was zu einer konservativen Auslegung führt, da die Plastizitätsfläche dem Tresca-Modell ähnelt, das von der ersten Spannungsinvariante unabhängig ist. Weitere Informationen finden Sie unter Theoretischer Hintergrund [2].
Modellaufbau
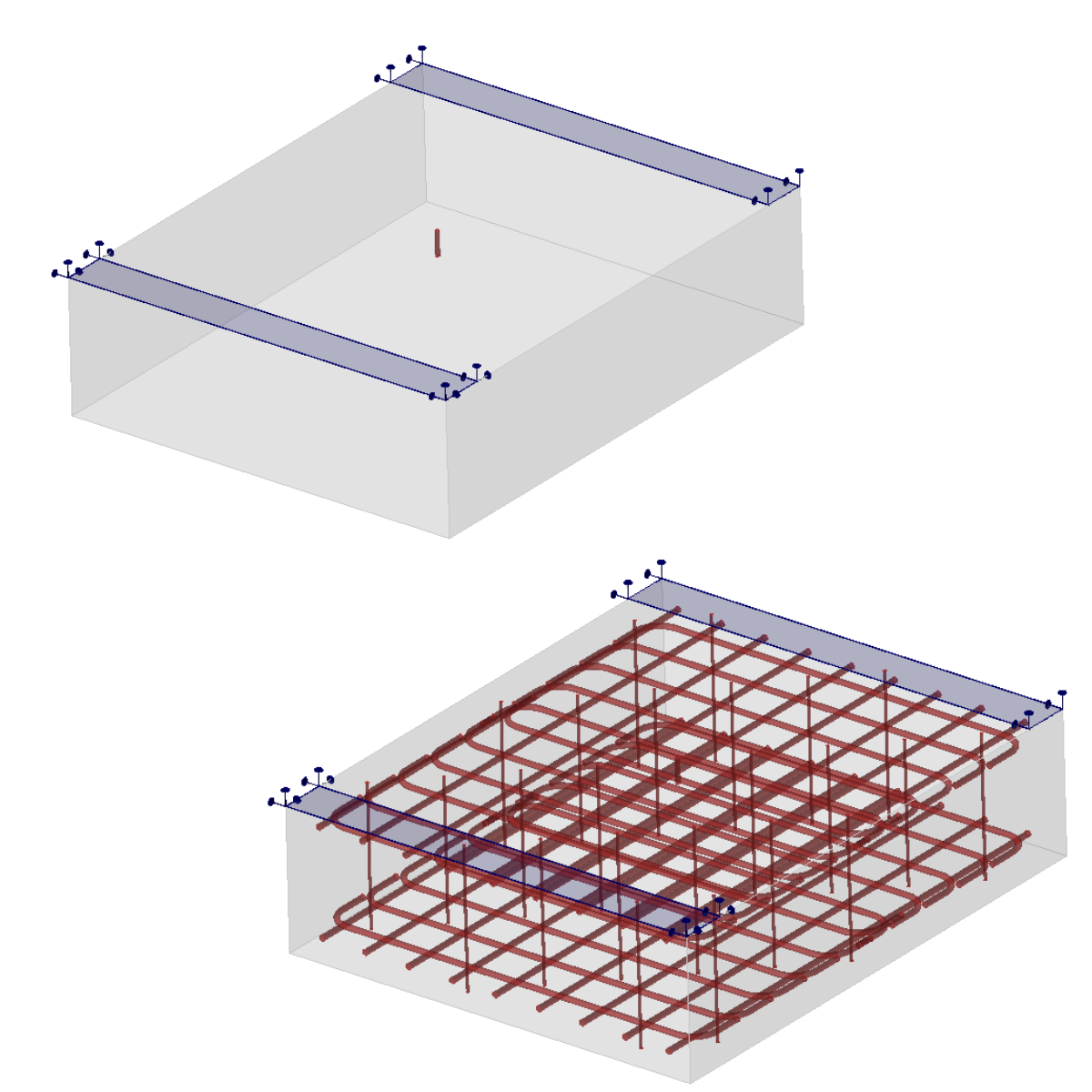
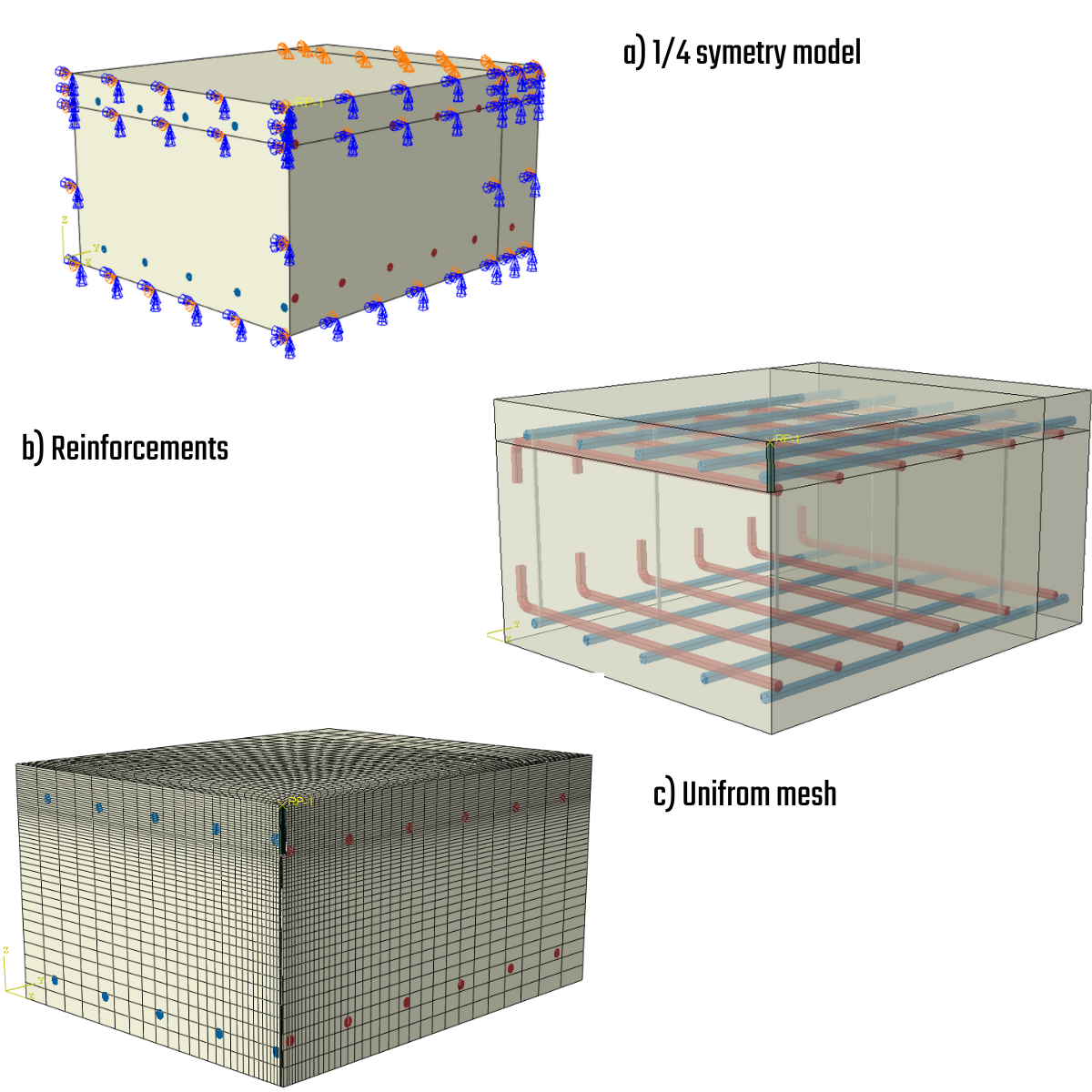
Das FEA-Modell wird mit tetraedrischen Betonelementen höherer Ordnung aufgebaut, wobei eingebettete 1D-Stäbe die Bewehrung darstellen, die über MPC (Multi-Point-Constraints) und Verbundelemente miteinander verbunden sind, um ein Gleiten zu ermöglichen. Die Bewehrungsstäbe sind in zwei Oberflächenschichten mit einer Überdeckung von 60 mm und Scherverbindungen aufgeteilt (siehe Abb. 2). Das Modell verwendet eine Flächenlagerung mit eingeschränkten X-, Y- und Z-Freiheitsgraden auf einer Breite von 200 mm. Gegossene Anker werden in der Mitte des Probekörpers positioniert, und die Länge des Ankers variiert von 100-200 mm, um alle möglichen Versagensarten zu testen.
3) Montage des Modells
Modell des Ankers
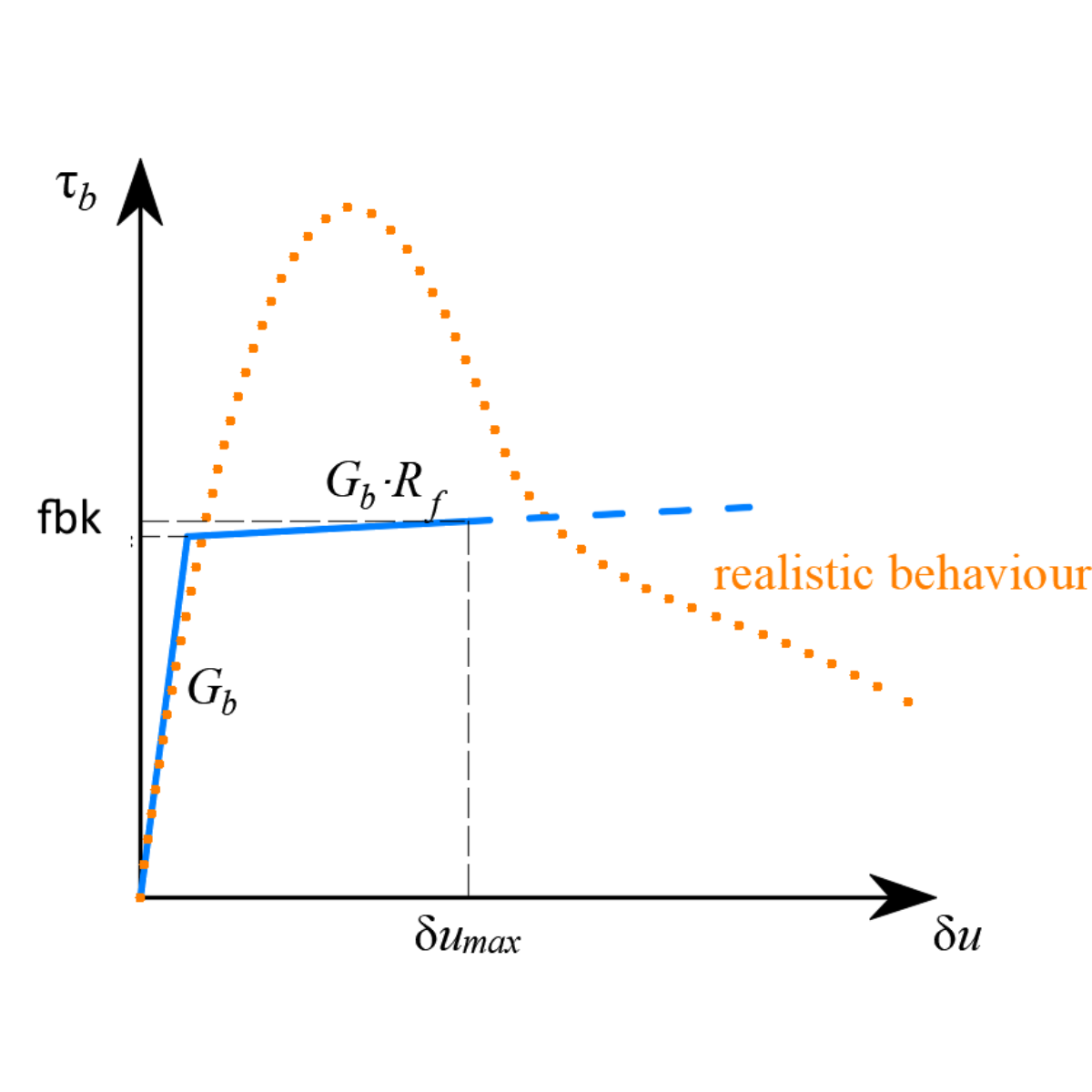
Der Anker wird mit einem Fachwerkelement modelliert, das nur Druck und Zug übertragen kann. Wichtig ist das Verbundmodell und wie der Anker mit dem umgebenden Beton verbunden ist, um den Kraft- und Spannungsfluss bei einer Interaktion zwischen Beton, Anker und Bewehrung zu gewährleisten. Die Verbindung hat eine spezifische lineare SchersteifigkeitGb, die vom Elastizitätsmodul des Betons Ecm und dem Durchmesser des Ankers abhängt. Mehr über das Verbundmodell finden Sie in Theoretischer Hintergrund [2].
4) Verbundmodell und MPC
Bemessungsnormen
CEB-FIB Modus Code 2020
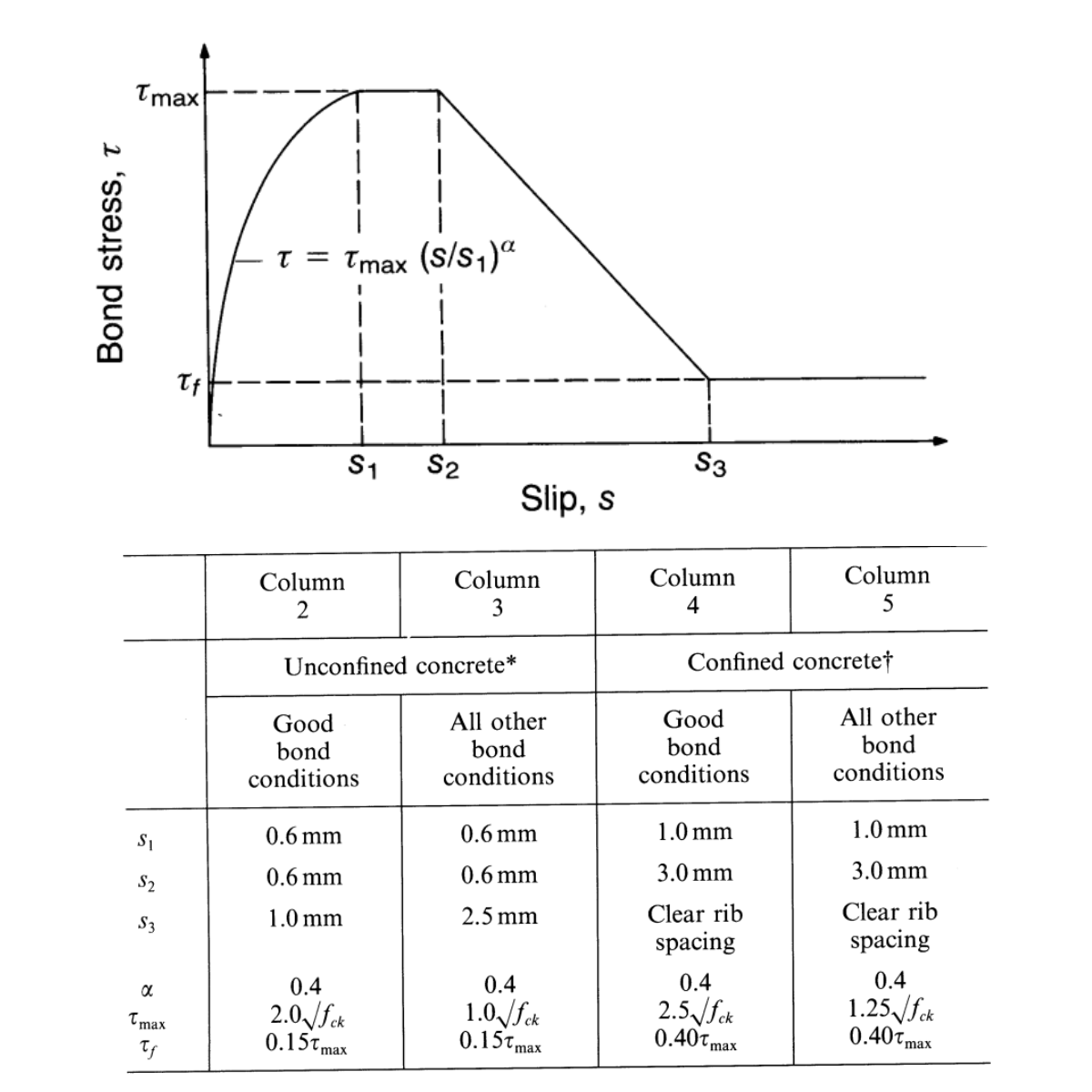
Die Ingenieure haben die Unterstützung im Code und in den gültigen Normen. Diese Aussage gibt den Anstoß, die experimentelle Lösung mit den Code-Lösungen zu vergleichen, um die Sicherheit der aktuellen Normen und Codes zu überprüfen. Die Betoneigenschaften C40/50 wurden aus den Code-Eigenschaften übernommen. Die Materialeigenschaften von Bewehrungsstäben und Verankerungen wurden experimentell geprüft und die Daten wurden bereitgestellt. Wir haben die Lösung für ungespannten Beton und die Unterkategorie der guten/anderen Verbundbedingungen überprüft. Der CEB-FIB-Moduscode [3] bietet eine klare Definition der Funktionsweise des Verbunds. Die Eingaben wurden für die numerische Simulation des Dübels in ABAQUS [4] verwendet.
4) CEB-FIB mode code 2020 - Verbundmodell
Eurocode 1992-1-1
Die Annahme des Eurocode 1992-1-1 [5] wurde als Voraussetzung für 3D CSFM verwendet. Das starr-plastische Modell mit einem charakteristischen und experimentell berechneten Bindungsmodell wurde für die Simulation und den Vergleich mit einer experimentellen Lösung verwendet.
5) Eurocode 1992-1-1 und 3D CSFM - Bindungsmodell
Eurocode 1992-4
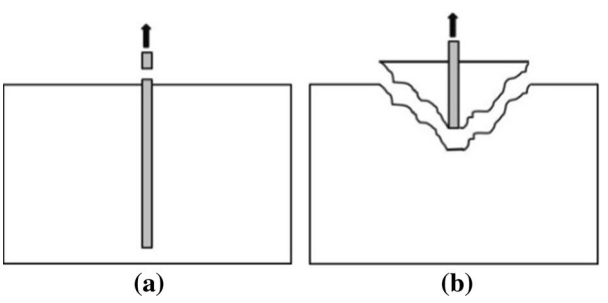
Die charakteristischen Werte wurden auch mit dem Eurocode 1992-4 [6] verglichen, der in IDEA StatiCa Connection implementiert ist. Dies gibt Aufschluss darüber, wie die Bewehrung im Betonblock das lokale Verhalten des Dübels beeinflusst. Es ermöglicht die Überprüfung von Effekten wie dem Versagen des Ankers auf Zug und dem Ausbrechen des Betonkegels.
6) a) Stabversagen auf Zug; b) Betonkonusausbruch
ABAQUS - Betonschädigung Plastizität
Annahmen
Concrete Damage Plasticity (nachfolgend CDP) basiert auf dem Drucker-Prager-Plastizitätszustand [7]. Dieses Modell eignet sich für Materialien mit innerer Reibung, wie z.B. Böden oder Beton. Die Zugfestigkeit ist deutlich geringer als die Druckfestigkeit, und der hydrostatische Teil des Spannungstensors spielt eine Rolle bei der Entwicklung der Plastizitätsfläche. Unter allgemeiner Spannung hat der Plastizitätszustand die Oberfläche eines rotierenden Kegels. Das Materialmodell für Druck- und Zugspannungen berücksichtigt auch das postkritische Verhalten, das durch die so genannten Schädigungsparameter gesteuert wird, die Werte von Null (ungeschädigt) bis Eins annehmen (für eine Steifigkeit des Betons in Druck oder Zug im postkritischen Zustand nahe Null).
Materialmodelle
Das einachsige Materialmodell in Druck und Zug für Beton basiert auf der Theorie von Thorenfeldt [8]. Alle Eingaben sind charakteristische Werte, die dem Zuverlässigkeitsansatz von EN 1992-1-1 [5] folgen. Die Parameter für das Materialmodell der Bewehrung und des Ankers sind dem Kapitel "Experimentelle Beschreibung" entnommen, wobei die lineare Verfestigung im plastischen Zweig des Diagramms berücksichtigt wird.
FEA-Elemente
Für das FEM-Modell des Betons wurde das C3D8, ein Hexa-Element mit einer linearen Basisfunktion und acht Integrationspunkten, verwendet. Der Beton und die Bewehrung bestehen aus T3D2-Elementen, die nur axiale Effekte übertragen. Die Interaktion zwischen der Bewehrung und dem Beton wird durch MPC-Zwangsbedingungen gewährleistet, bei denen die Zugversteifung berücksichtigt wird, was bis zu einem gewissen Grad das Kohäsionsmodell oder den Dübeleffekt abdeckt.
Modellaufbau
Das FEA-Modell wird mit symmetrischen Randbedingungen aufgebaut, um die Berechnungskosten zu minimieren und die Effizienz und Geschwindigkeit der Lösung zu verbessern. Es ist wichtig zu beachten, dass aufgrund des reduzierten Modells die auf den Anker wirkenden Kräfte ein Viertel der Maximalkraft erreichen werden.
7) Montage des Modells
Anker
Der Anker wird mit 3D-Volumenelementen modelliert. Für die Modellierung des Verbundes zwischen Beton und Anker wurde das kontaktkohäsive Verhalten verwendet. Die Oberflächeninteraktion ermöglicht eine Delamination auf der Grundlage des linear-elastischen Zug-Trennungs-Gesetzes, bevor eine Schädigung auftritt. Harter Kontakt wurde bei Druck und reibungsfreies Verhalten bei tangentialen Bewegungen verwendet. Das kohäsive Verhalten in Normal- und Scherrichtung wurde mit Hilfe von volumetrischen Steifigkeits- und Schädigungsparametern eingeführt, um postkritisches Verhalten darzustellen. Die Auslösung des nachkritischen Verhaltens wird durch die maximale Verbundspannung in Normal- und Scherrichtung und die Bruchenergie mit linearer oder exponentieller Erweichung ausgedrückt [7].
8) Kohäsiver Kontakt
Ergebnisse - Anker 100 mm
9) Input-Output notwendige Eigenschaften für die Simulation
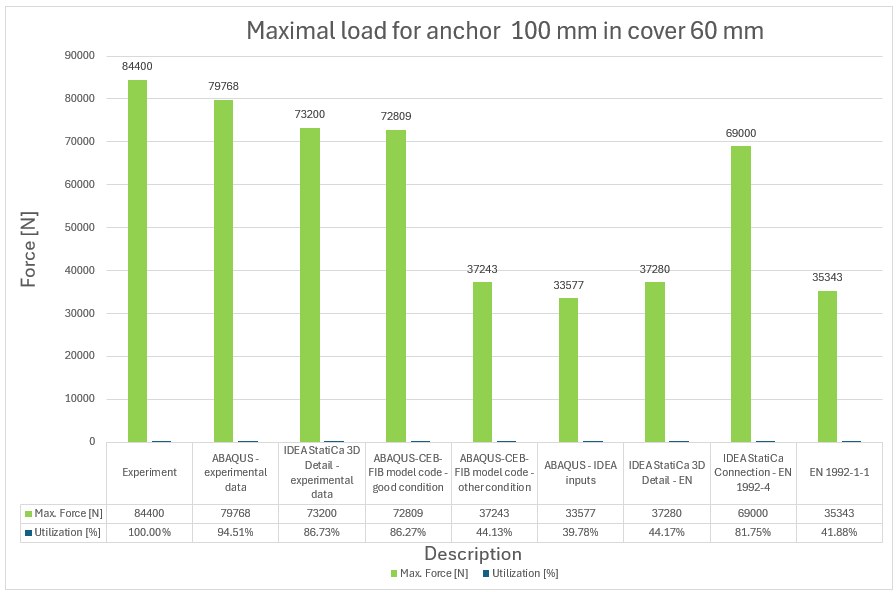
10) Maximale Kraft und Auslastung im Vergleich zum Experiment für Anker 100 mm
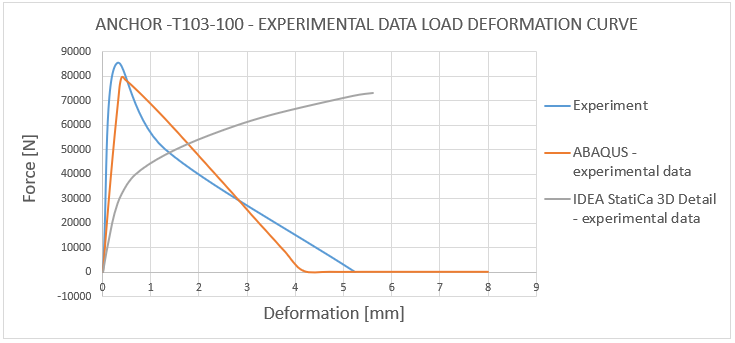
11) Lastverformungskurve - Vergleich der experimentellen Daten von T103-100
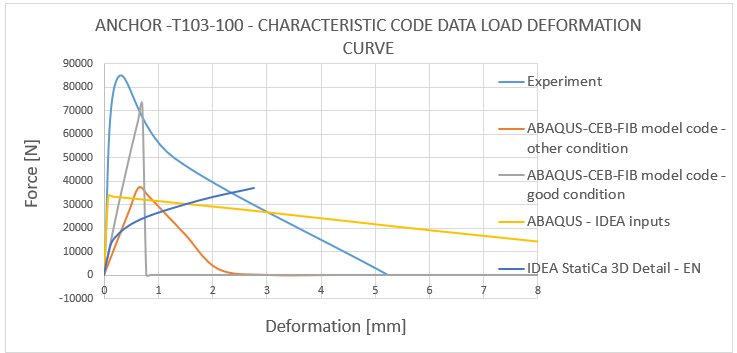
12) Lastverformungskurve - Vergleich der charakteristischen Code-Daten von T103-100
Ergebnisse - Anker 150 mm
12) Für die Simulation erforderliche Input-Output-Eigenschaften
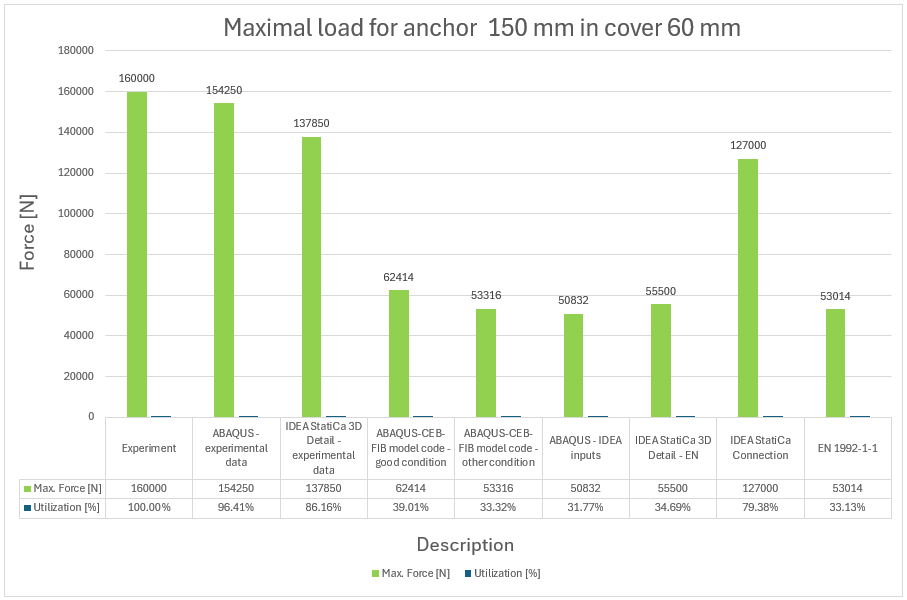
13) Maximale Kraft und Ausnutzung im Vergleich zum Experiment für Anker 150 mm
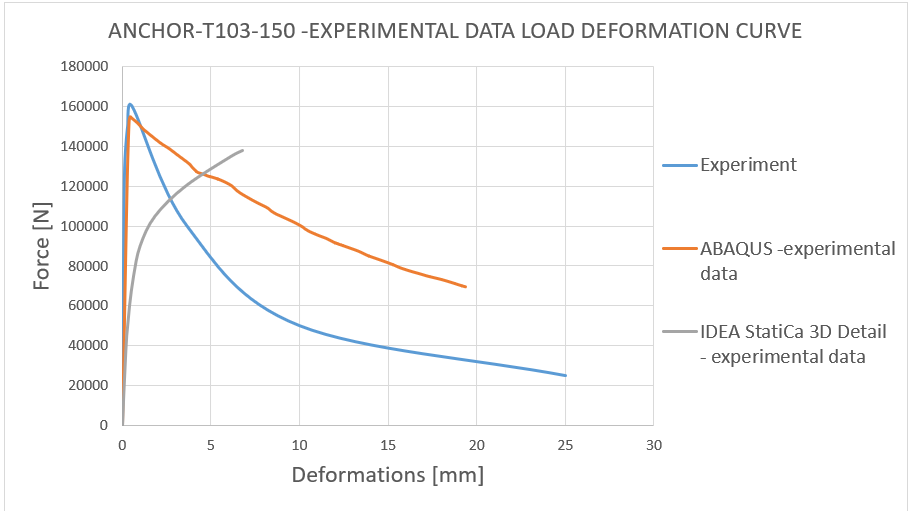
14) Lastverformungskurve - Vergleich der experimentellen Daten von T103-150
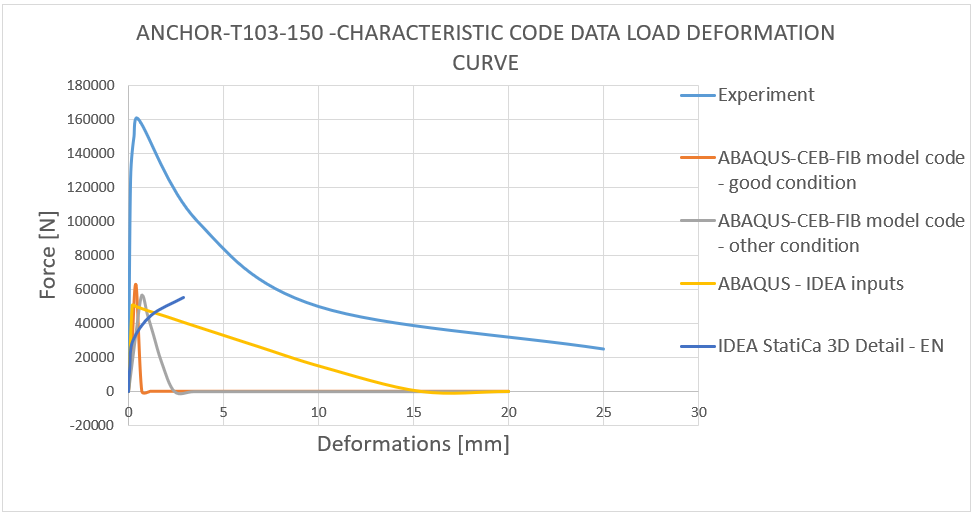
15) Lastverformungskurve - Vergleich der charakteristischen Code-Daten von T103-100
Ergebnisse - Anker 200 mm
16) Für die Simulation erforderliche Input-Output-Eigenschaften
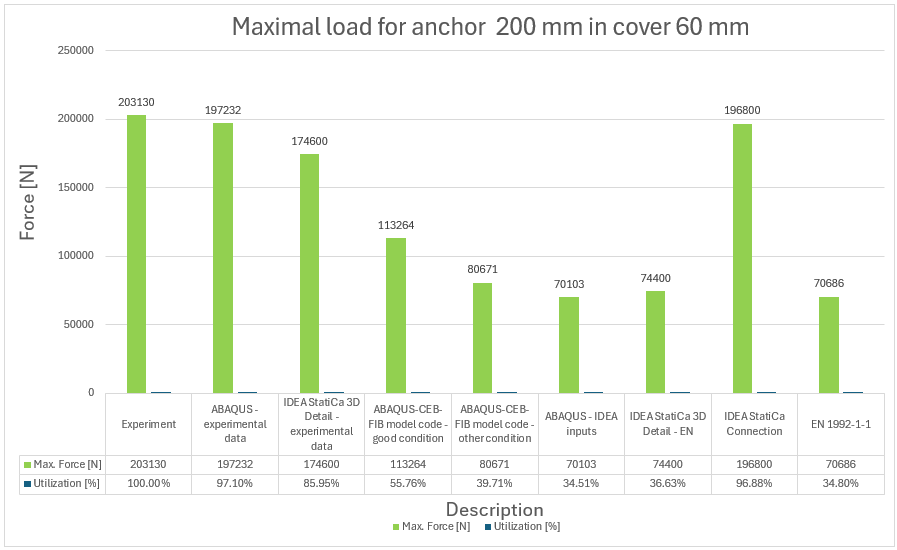
17) Maximale Kraft und Auslastung im Vergleich zum Experiment für Anker 200 mm
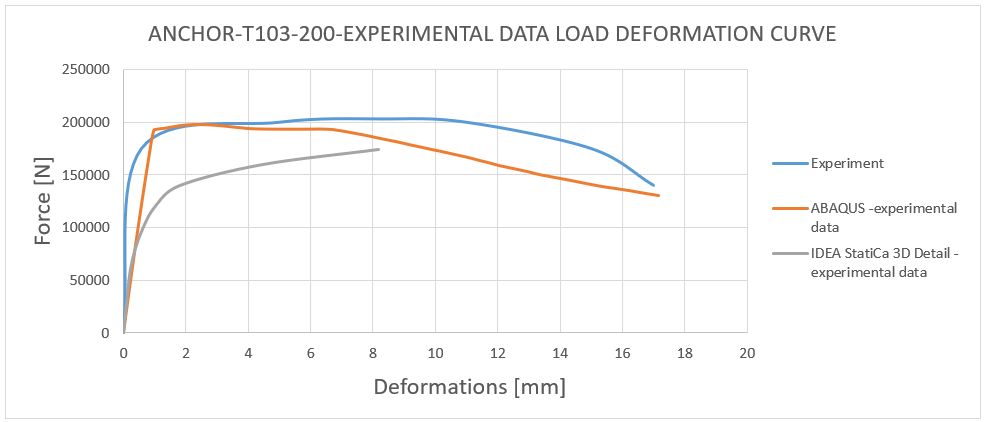
18) Lastverformungskurve - Vergleich der experimentellen Daten des T103-200
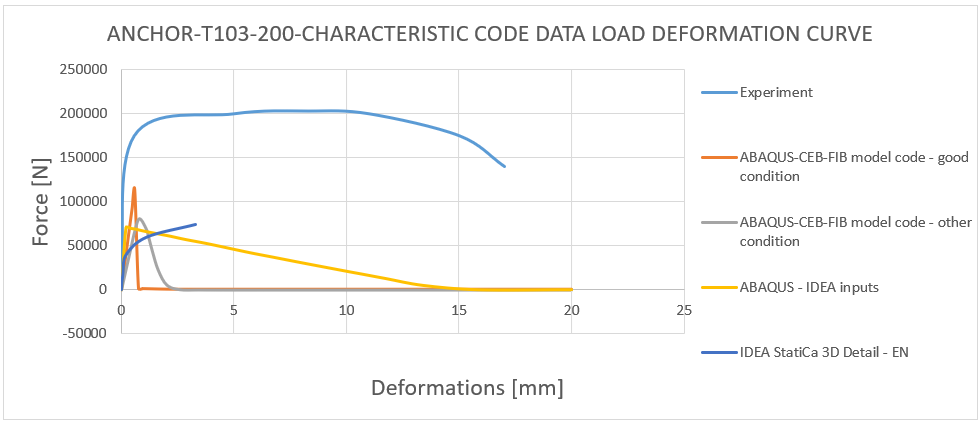
19) Lastverformungskurve - Vergleich der charakteristischen Code-Daten von T103-200
Fazit
Die Versuchskampagne untersuchte erfolgreich das Verhalten von Ankern in voller Größe, die in einen Stahlbetonblock einbetoniert sind, unter Verwendung eines umfassenden Ansatzes, der sowohl experimentelle Tests als auch numerische Modellierung umfasst. Durch Variation der Einbindetiefen der Anker (100, 150, 200 mm) konnten verschiedene Versagensarten beobachtet werden, darunter Verbundversagen, Betonkonusausbruch und Stabversagen. Die Ergebnisse wurden streng mit den Vorhersagen des CEB-FIB-Modellcodes und der Eurocodes verglichen, wodurch die Sicherheit und Zuverlässigkeit der aktuellen Bemessungsstandards für solche Verankerungssysteme bestätigt wurde.
Der Einsatz fortschrittlicher Modellierungstechniken wie 3D CSFM und ABAQUS-Simulationen mit Concrete Damage Plasticity ermöglichte tiefere Einblicke in die Interaktion zwischen Beton und Bewehrung sowie in das Verbundverhalten unter quasistatischer Zugbelastung. Die Ergebnisse bestätigten die Wirksamkeit der vorgeschlagenen Methoden bei der Vorhersage der Ankerleistung und betonten die Bedeutung einer genauen Materialmodellierung und geeigneter Randbedingungen bei solchen Simulationen.
Der Vergleich zwischen dem tatsächlichen Verhalten, das während des Experiments beobachtet wurde, und der numerischen Lösung, die mit 3D CSFM und ABAQUS abgeleitet wurde, zeigt eine Korrelation von ungefähr 85 %. Daraus lässt sich schließen, dass keine numerische Lösung die experimentellen Daten übertrifft und eine Fehlermarge von 15 % im Vergleich zum Experiment beibehält, was aus technischer Sicht als akzeptabel angesehen wird. Wichtig ist auch, dass die Versagensarten übereinstimmen, mit Ausnahme der Ankerlänge von 200 mm, bei der in 3D CSFM eine kombinierte Versagensart von Betonkonus und Herausziehen vor dem Versagen der Stahlstange auftrat. Der Grund dafür ist, dass in diesem Fall die Spitzenlasten, die diesen beiden Versagensarten entsprechen, sehr nahe beieinander liegen.
Die Ergebnisse von CEB-FIB Mode Code 2020 und Eurocode 1992-1-1 stimmen mit den experimentellen Ergebnissen zu 30-40 % überein. Dies zeigt, dass der im Code verwendete Ansatz Sicherheit gewährleistet. Es ist wichtig zu beachten, dass es sich bei den ermittelten Werten um charakteristische Werte und nicht um Bemessungswerte handelt, so dass die tatsächliche Bemessungsfestigkeit noch niedriger ist.
Die Ergebnisse des Berichts sollen den Ingenieuren vermitteln, dass die 3D-CSFM-Methode sichere Ergebnisse in Übereinstimmung mit dem Eurocode 1992-1-1[5] liefert und zu einer konservativen Bemessung führt, die in die Norm selbst integriert ist.
Referenzen
[1]Delhomme, F. & Roure, Thierry & Arrieta, Benjamin & Limam, Ali. (2015). Auszugsverhalten von eingegossenen Kopf- und Verbundankern mit unterschiedlichen Verankerungstiefen. Materials and Structures. 49. 10.1617/s11527-015-0616-4.
[2] "IDEA StatiCa Detail - Statische Bemessung von 3D-Diskontinuitäten aus Beton (BETA)". IDEA StatiCa Support Center, 2023. https://www.ideastatica.com/support-center/idea-statica-detail-structural-design-of-concrete-3d-discontinuities-beta
[3] International Federation for Structural Concrete (fib). fib Model Code 2020 for Concrete Structures. Berlin: Ernst & Sohn, 2021.
[4] ABAQUS Standard User's Manual, Version 6.6*. Washington University in St. Louis, 2006.[https://classes.engineering.wustl.edu/2009/spring/mase5513/abaqus/docs/v6.6/books/stm/default.htm]
[5] Europäisches Komitee für Normung (CEN). EN 1992-1-1:2004: Eurocode 2 - Bemessung und Konstruktion von Betontragwerken - Teil 1-1: Allgemeine Regeln und Regeln für Bauwerke. Dezember 2004. https://www.phd.eng.br/wp-content/uploads/2015/12/en.1992.1.1.2004.pdf.
[6] Europäisches Komitee für Normung (CEN). EN 1992-4:2018: Eurocode 2 - Bemessung und Konstruktion von Betontragwerken - Teil 4: Bemessung und Konstruktion von Befestigungsmitteln für die Verwendung in Beton. Brüssel: CEN, April 2018
[7]ABAQUS, Inc. ABAQUS User Subroutines Reference Manual, Version 6.6. Washington University in St. Louis, 2006. https://classes.engineering.wustl.edu/2009/spring/mase5513/abaqus/docs/v6.6/books/usb/default.htm?startat=pt05ch18s05abm36.html.
[8] Massone, L. M.; et al. Shear-Flexure Interaction for Structural Walls, 2006. ResearchGate. https://www. researchgate.net/publication/284079633_Shear-flexure_interaction_for_structural_walls (Zugriff am 01. Januar 2006).