Connection design can be difficult to teach, given the detailed nature of the topic and the fundamentally three-dimensional behavior of most connections. However, connections are critically important, and lessons learned in the study of connection design, including load path and identification and evaluation of failure modes, are general and applicable to structural design broadly. IDEA StatiCa uses a rigorous nonlinear analysis model and has an easy-to-use interface with a three-dimensional display of results (e.g., deformed shape, stress, plastic strain) and thus is well suited for the exploration of the behavior of structural steel connections. Building on these strengths, a suite of guided exercises that use IDEA StatiCa as a virtual laboratory to help students learn about concepts in structural steel connection behavior and design was developed. These learning modules were primarily targeted to advanced undergraduate and graduate students but were made suitable for practicing engineers as well. The learning modules were developed at Laboratory for Numerical Structural Design by Assistent Professor Martin Vild from the Brno University of Technology.
Learning Objective
After performing this exercise, the learner should be able to describe the basic component of bolted connections, T-stub and associated phenomena, like prying action.
Background
Component method in EN 1993-1-8 divides the connection into components. The basic component of bolted connections, widely used for assembly joints, is T-stub. The shape of the T-stub varies depending on its location in the connection, but the calculation remains very similar. Even such a complicated haunched end-plate connection is divided between eight rows of T-stubs. Each such a T-stub is calculated individually or as a part of a bolt group, and the ultimate moment resistance is the sum of T-stub tensile resistance times the lever arm to the center of compression.
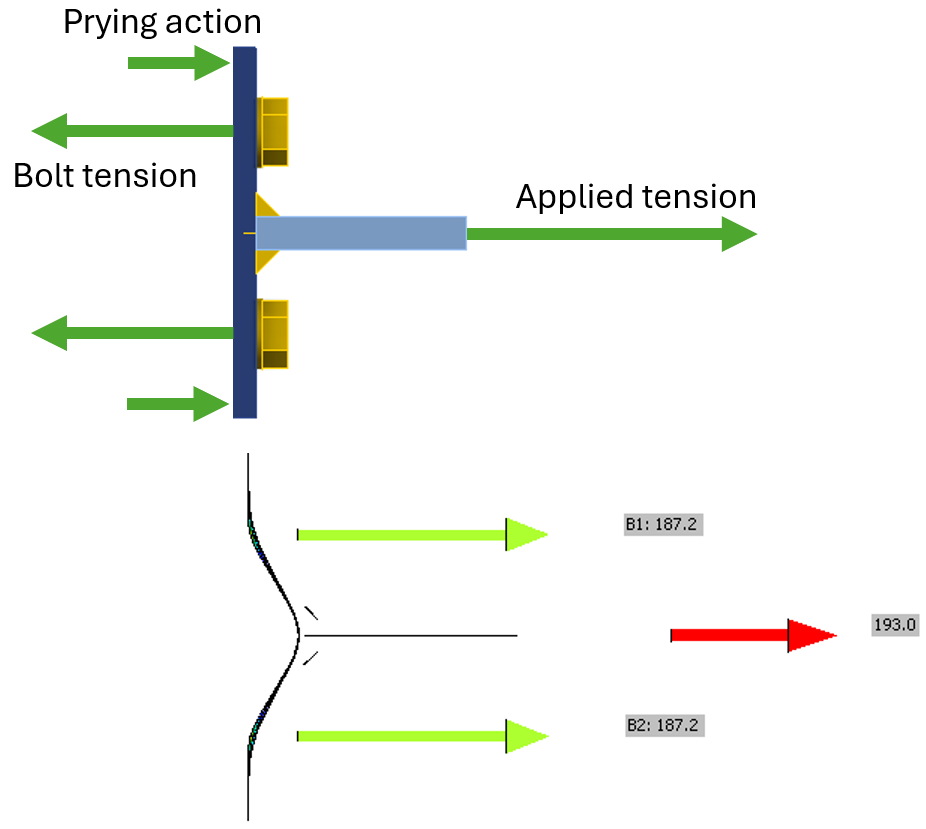
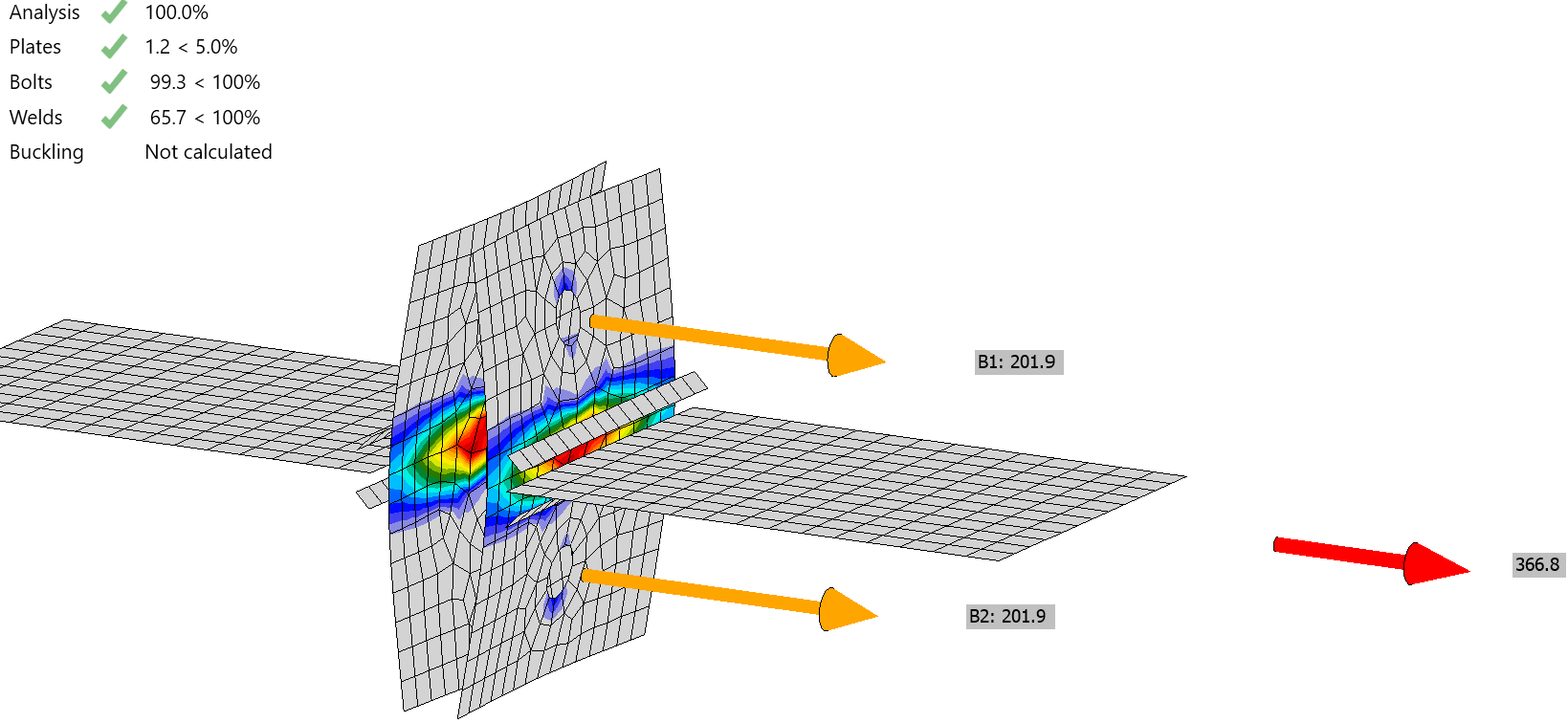
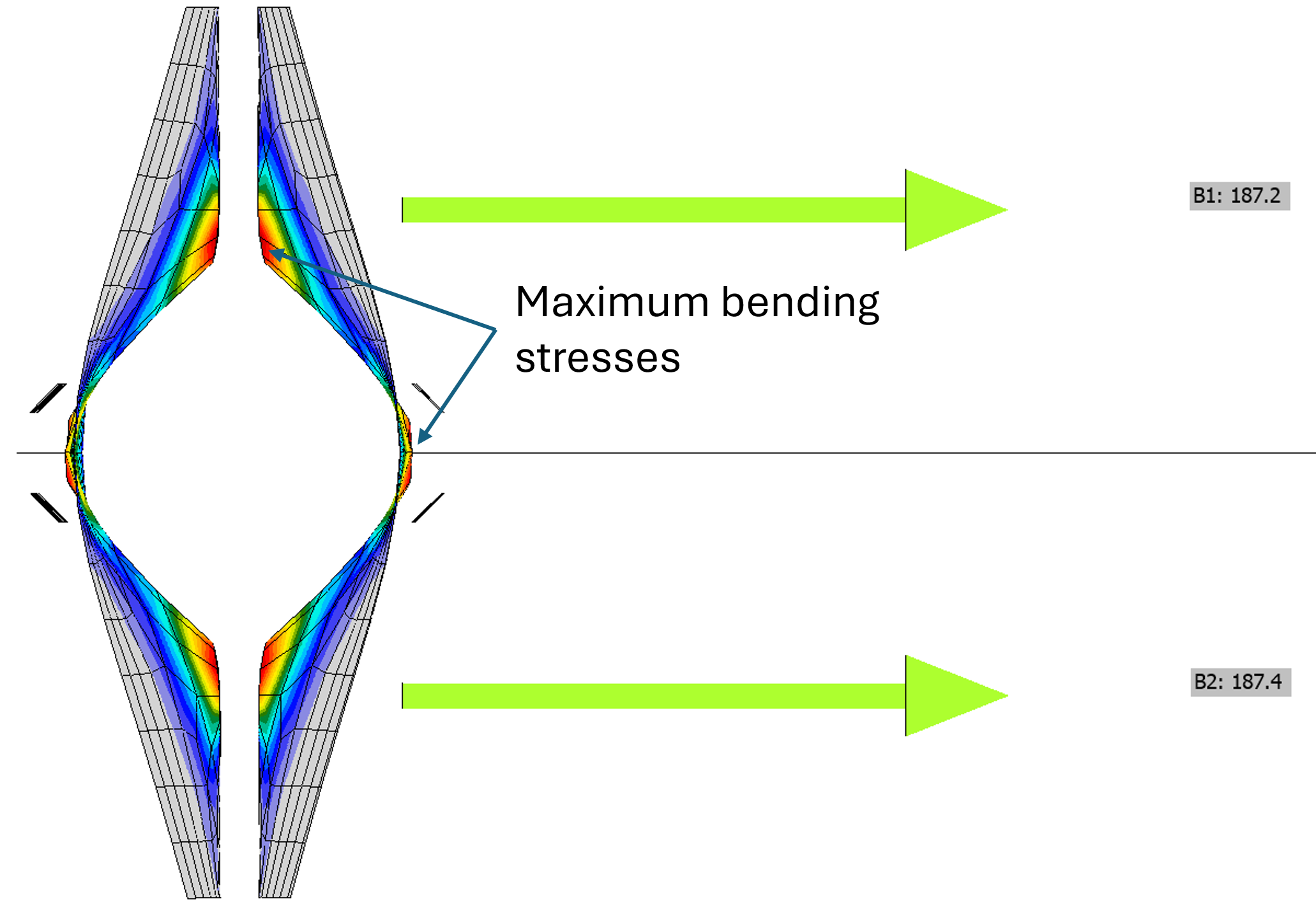
A typical feature of T-stubs is prying action. The sum of tension in bolts is higher than the applied tension to T-stub. This is caused by prying – a bearing action of plates to the support, typically another T-stub, in this case consisting of the column flange and web. Notice that the sum of bolt tensile forces in the following figure is \(2 \cdot 187.2 = 374.4\) kN, which is significantly more than 193 kN of applied force.
The magnitude of the bearing force depends on the stiffness and strength of the connected elements and bolts.
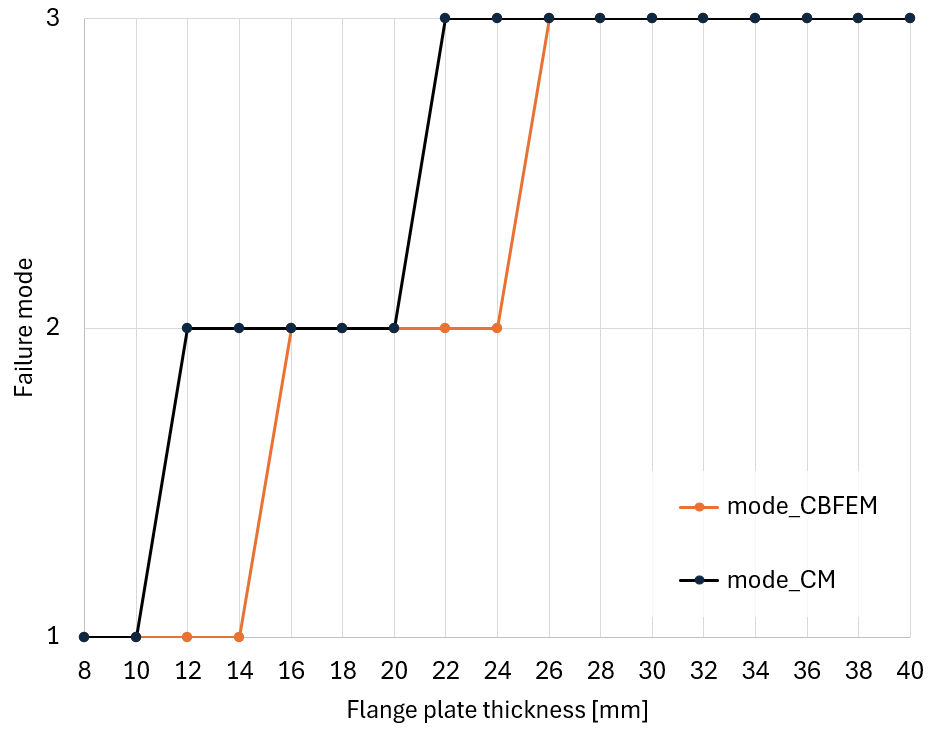
- If the end plate is very thin, it will yield both near the weld and near the bolt line, and the strength of the end plate will control even when considering additional tension in the bolts due to prying action. The Eurocode describes this as failure mode 1.
- If the end plate is very thick, it will not bend enough to overcome the elongation of the bolt, and the end plate will not contact the column flange. In this case, there is no prying action, the strength of the bolts will control, and a simple analysis is sufficient to estimate the force in the bolts. The Eurocode describes this as Mode 3.
- For end-plate thicknesses between these extremes, the flexural strength of the angles and the tensile strength of the bolts can control simultaneously.
In Eurocode 3 (CEN, 2005), these different behaviors are called “Mode 1: Complete yielding of the flange”; “Mode 2: Bolt failure with yielding of the flange”; and “Mode 3: Bolt failure” and correspond to thin, intermediate, and thick connecting elements, respectively.
Equations to assess prying action are included in Eurocode EN 1993-1-8, Cl. 6.2.4. These equations can be used to efficiently assess prying action, but they use abstracted parameters that obscure the physical behavior. This exercise is intended to help develop physical intuition on prying action.
Connection
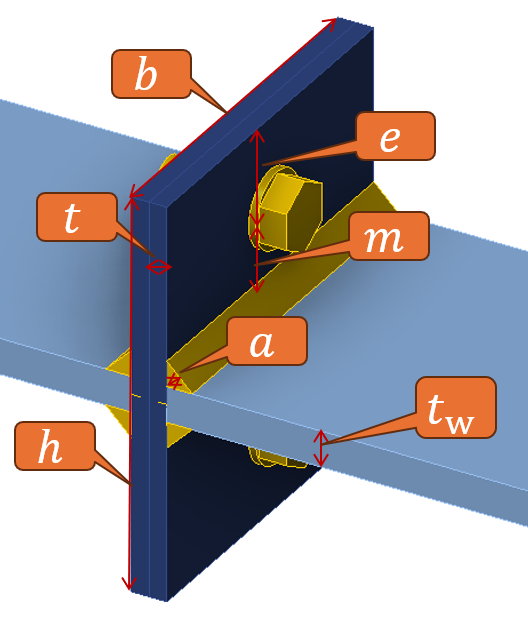
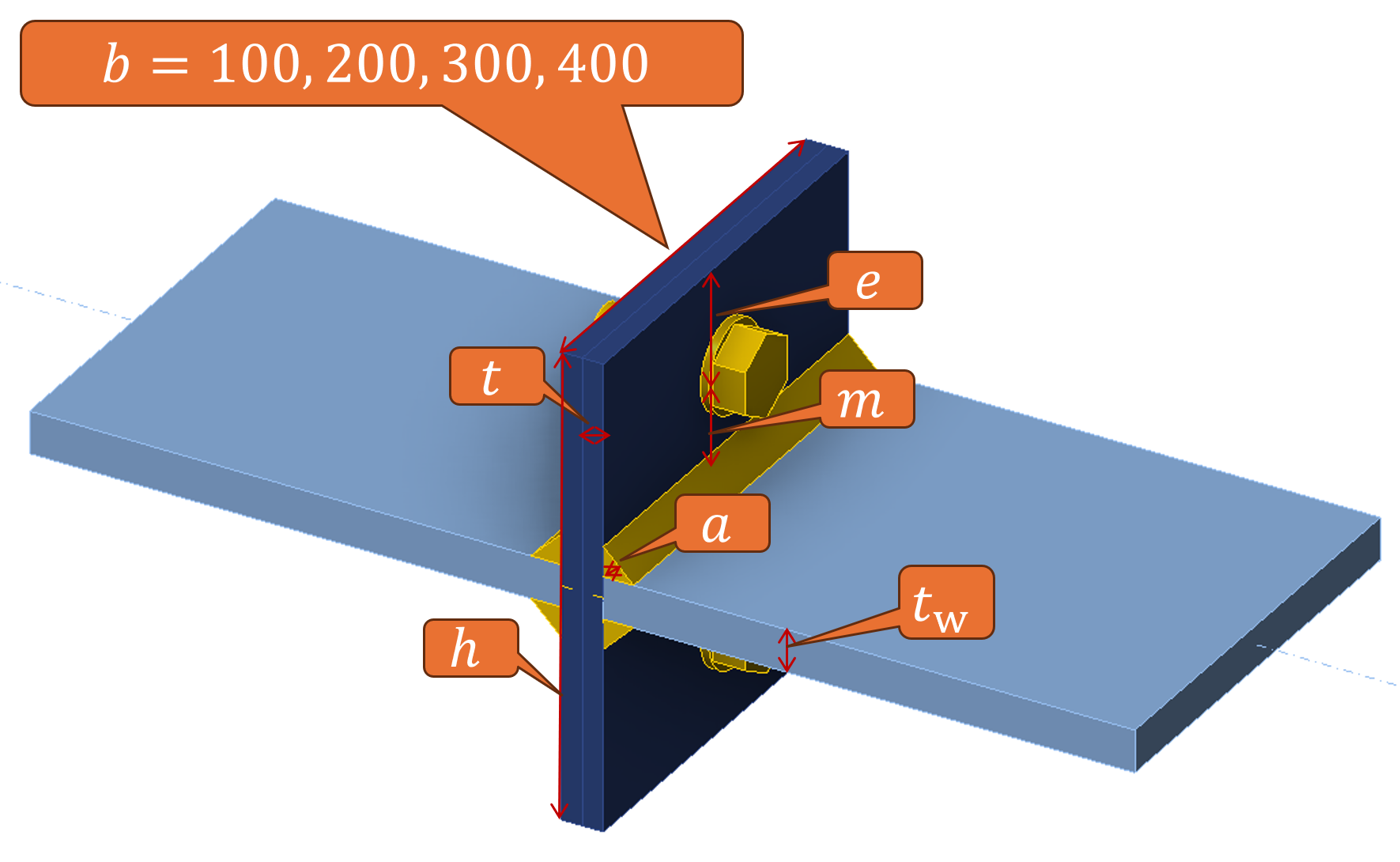
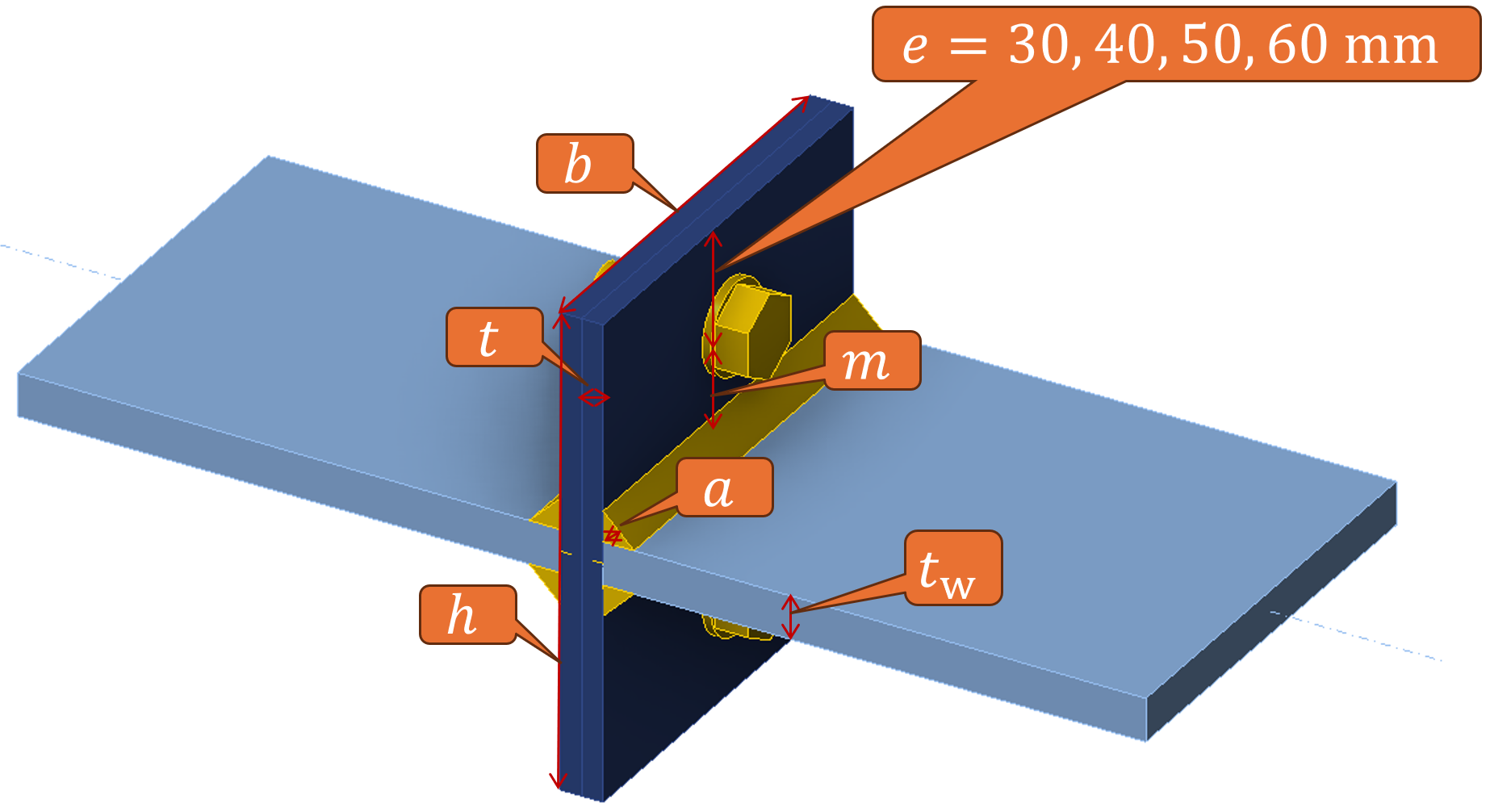
The connection examined in this exercise is the basic example of two identical T-stubs oriented back-to-back. The basic case consists of two end plates (or T-stub flanges) with the dimensions \(b \cdot h = 200 \cdot 220\) mm and the thickness of \(t = 20\) mm. Tensioned plates (or T-stub webs) are 20 mm thick. All elements are from S355 steel grade. Double fillet welds with the throat thickness of 10 mm connect the T-stub webs to flanges. T-stub flanges are connected by M24 8.8 bolts (\(d = 24\) mm, \(f_u = 800\) MPa). The bolts are in the middle of the T-stub and their edge distance is \(e = 50\) mm.
Procedure
The procedure for this exercise assumes that the learner has a working knowledge of how to use IDEA StatiCa (e.g., how to navigate the software, define and edit operations, perform analyses, and look up results). Guidance for how to develop such knowledge is available on the IDEA StatiCa website (https://www.ideastatica.com/).
Retrieve the IDEA StatiCa file for the example connection provided with this exercise. Open the file in IDEA StatiCa. To perform the exercise, follow the narrative, complete the tasks, and answer the questions.
The learner is provided with two helper files:
- T-stub calculation-Calcpad.zip – a hand calculation in an open-source Calcpad
- T-stub.py – a Python code for the automation of IDEA StatiCa using its API
Running these files is not mandatory to complete the learning module, but they speed up the hand calculation.
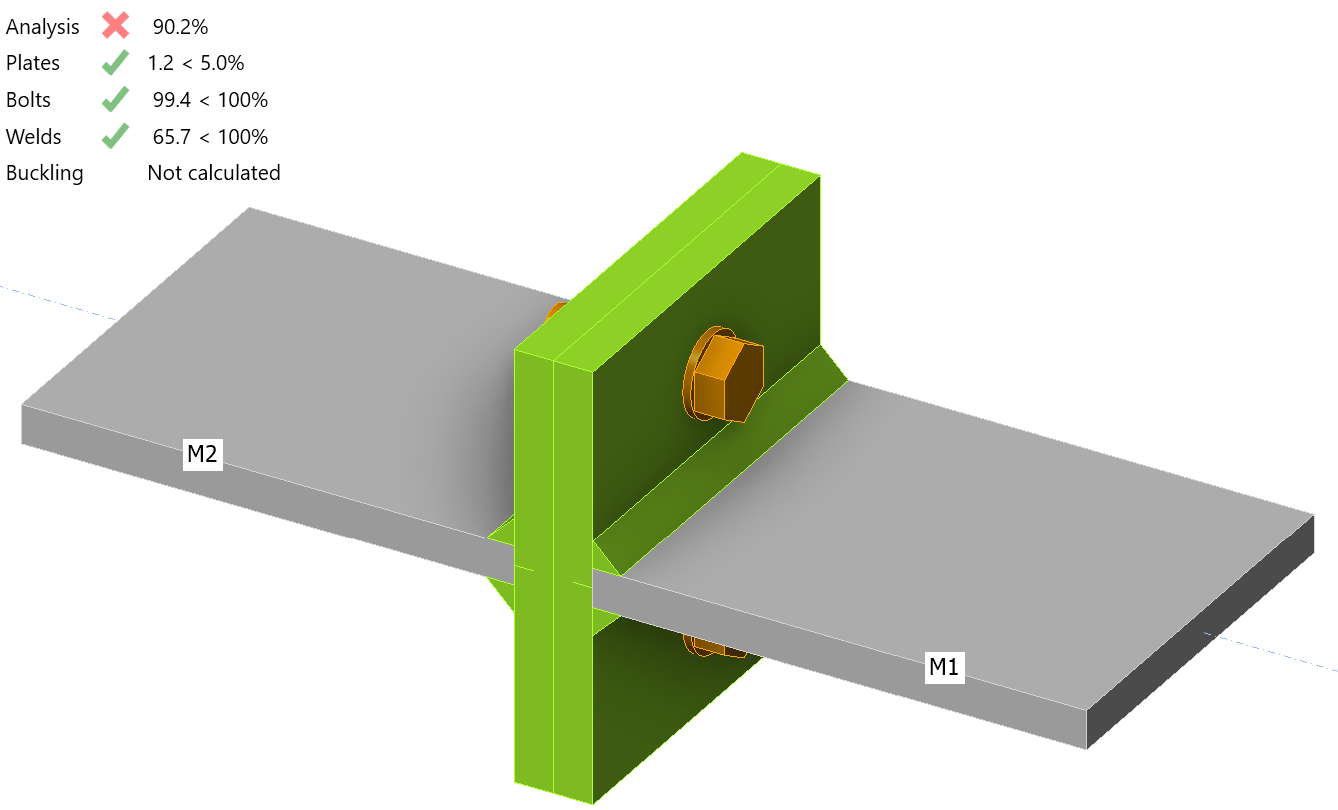
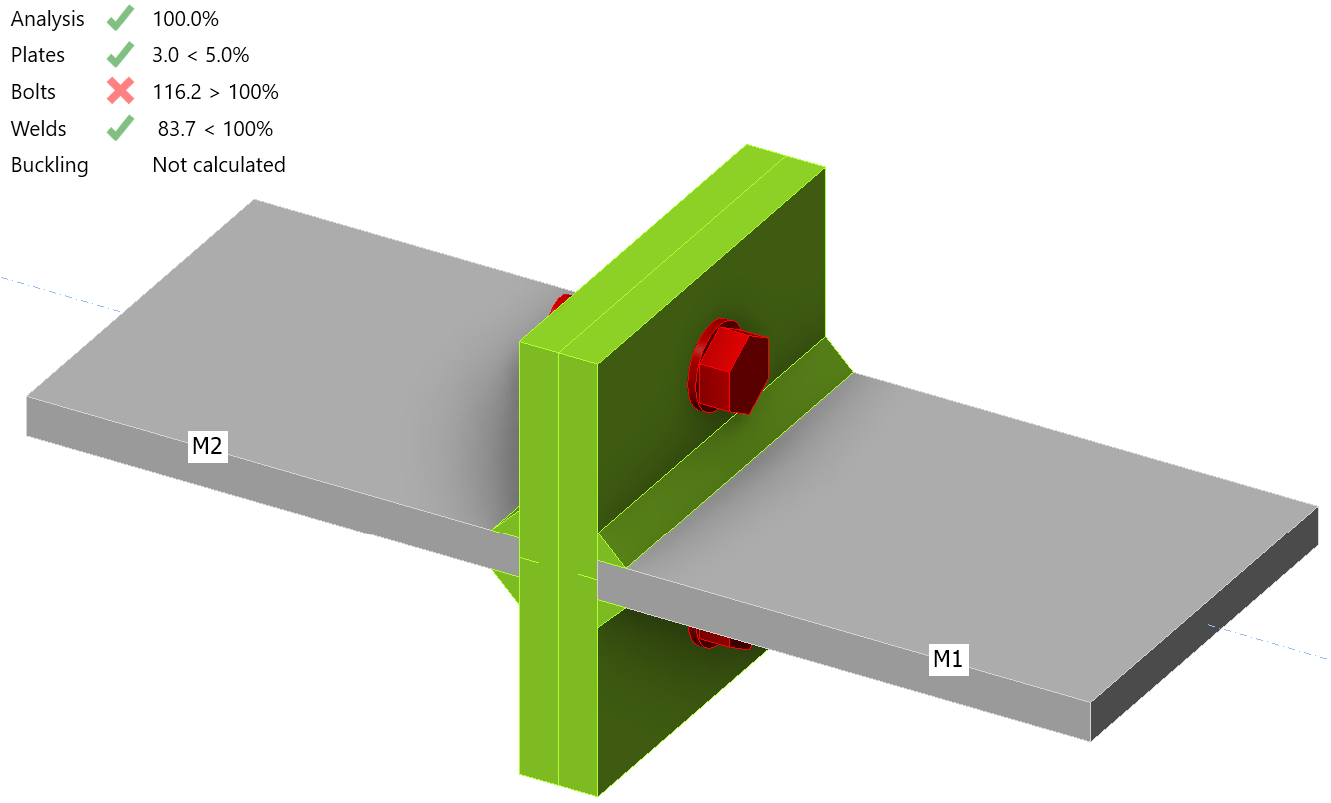
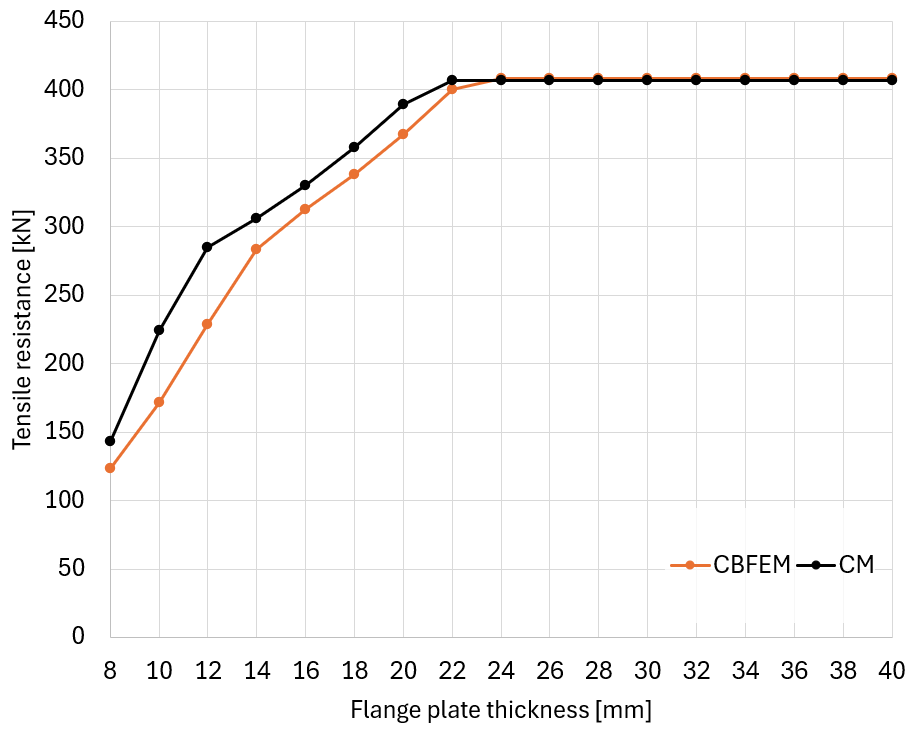
Complete the table shown below by determining the maximum force that the connection can support for a variety flange plate thickness, then recording that force along with the maximum plastic strain and maximum bolt utilization at that force.
| Flange plate thickness [mm] | Maximum force [kN] | Maximum plastic strain [%] | Bolt utilization [%] |
| 8 | 123.0 | 4.16 | 90.9 |
| 10 | |||
| 12 | 228.5 | 4.87 | 97.4 |
| 14 | 283.2 | 4.03 | 99.5 |
| 16 | 312.5 | 1.90 | 99.4 |
| 18 | 337.9 | 1.40 | 99.3 |
| 20 | |||
| 22 | 400.4 | 1.20 | 99.8 |
| 24 | 408.2 | 0.32 | 99.6 |
| 26 | 408.2 | 0.11 | 99.6 |
| 28 | 408.2 | 0.05 | 99.6 |
| 30 | |||
| 32 | 408.2 | 0.00 | 99.6 |
| 34 | 408.2 | 0.00 | 99.6 |
| 36 | 408.2 | 0.00 | 99.6 |
| 38 | 408.2 | 0.00 | 99.6 |
| 40 |
Does the strength of the connection increase, decrease, or stay the same when the following dimensions are increased? Consider how the answer might be different for different flange plate thicknesses.
Note that the hand calculation according to EN 1993-1-8 is well explained in SCI P398 on pages 10–17.
References
EN 1993-1-8:2005 Eurocode 3: Design of steel structures – Part 1-8: Design of joints, CEN, Brussels
SCI P398 Joints in Steel Construction: Moment-resisting Joints to Eurocode 3, 2013