Fissuras

A formação de fissuras

Uma caraterística das estruturas de betão armado sujeitas a tensões de flexão ou de tração é a ocorrência de fissuras nos pontos em que a tensão de tração no betão excede a resistência à tração do betão. Para a durabilidade da estrutura e também para a estética da estrutura, é importante assegurar que as fissuras resultantes sejam tão pequenas quanto possível. O cálculo das larguras das fissuras, bem como as larguras máximas permitidas para as diferentes classes de exposição, são apresentados na norma EN 1992-1-1, capítulo 7.3.

No primeiro passo do cálculo, determina-se se a secção transversal está fendilhada ou não. A largura da fenda em si é sempre calculada a partir da combinação de cargas quase permanentes ou frequentes (dependendo do anexo nacional), mas a formação de fendas tem de ser verificada a partir de todas as combinações SLS especificadas. Assim, podem ocorrer dois casos:

• A tensão máxima de tração nas fibras de betão não excederá a resistência à tração do betão a partir de qualquer combinação de cargas (_ME,qp quase permanente,_ME,fr frequente ou_ME,k caraterístico), pelo que se considera a secção transversal sem fissuras.

\[{{M}_{E,i}}\le {{M}_{cr}}={{f}_{ct,ef}}\frac{{I}_{I}}{h-{{a}_{I}}}\]

• Se as fendas se desenvolverem para qualquer uma das combinações (quase permanente, frequente ou caraterística), ou seja, o momento fletor desenvolvido a partir da combinação de cargas considerada é maior do que o momento crítico_Mcr, a secção está fendilhada a partir dessa combinação de cargas e as caraterísticas da secção fendilhada e a largura da fenda têm de ser calculadas.

\[{{M}_{E,i}}>{{M}_{cr}}={{f}_{ct,ef}}\frac{{I}_{I}}{h-{{a}_{I}}}\]

_ME,i. . o momento fletor obtido a partir de um pente de carga SLS. Assim, pode ser_ME,qp,_ME,fr ou_ME,k.

fct_,ef . . a resistência à tração do betão no momento considerado. Se o betão tiver mais de 28 dias, considera-se uma resistência igual a _fctm.

Cálculo da largura da fenda

Num elemento carregado por flexão, a formação de fendas divide-se em 2 fenómenos:

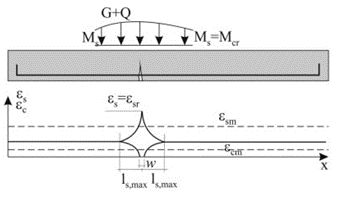
• Fase de formação de fissuras (etapa número 2 da Fig. 1)
• Desenvolvimento de fissuras estabilizadas (fase número 3 na Fig. 1)

\[ \textsf{\textit{\footnotesize{Fig. 1 Fases do comportamento da secção de betão armado durante o carregamento}}}\]

Fase de desenvolvimento da fissura

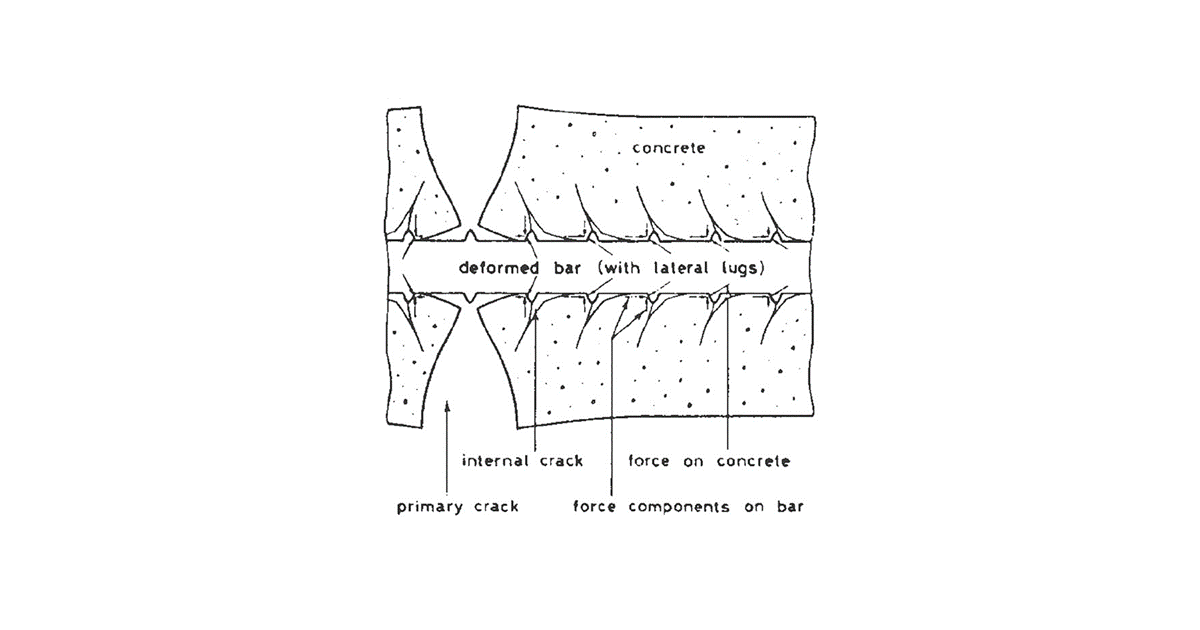
Esta é a parte inicial do processo quando as fendas individuais ainda estão a aparecer gradualmente até que toda a parte de tração da barra seja afetada por fendas que estão aproximadamente igualmente distribuídas ao longo do comprimento da barra. A primeira fissura é formada quando a força na tira tensionada excede o valor da força crítica_Nr (Força crítica de tração, ver abaixo), e outras fissuras desenvolvem-se até um nível de carga que exerce uma força na tira tensionada igual a aproximadamente 1,_3Ncr (fase número 2 na Fig. 1).

\[ \textsf{\textit{\footnotesize{Fig. 2 Tensões do betão e da armadura no momento da primeira fissura}}}\]

As fissuras em desenvolvimento dividem-se em 2 tipos - fissuras primárias e secundárias. As fissuras primárias ocorrem nas fibras de tração quando a resistência efectiva à tração do betão (fct_,eff) é atingida. As fissuras primárias representam o primeiro padrão de fissuras (Fig. 2). Entre as fissuras primárias formam-se depois fissuras secundárias mais curtas (Fig. 3). A tensões correspondentes a cerca de 1,2 a 1,5 _σsr (geralmente considera-se um valor médio de 1,3 _σsr, onde _σsr é a tensão na armadura na formação de fissuras primárias na zona de tração do betão), o desenvolvimento de fissuras secundárias também está concluído.

\[ \textsf{\textit{\footnotesize{Fig. 3 Fissuras primárias e secundárias}}\]

A largura da fenda na fase de formação da fenda pode ser calculada da seguinte forma:

\[{{w}_{k}}=2{{l}_{s,\max }}\left( {{\varepsilon }_{sm}}-{{\varepsilon }_{cm}} \right)\]

\[ \textsf{\textit{\footnotesize{Fig. 4 Caraterísticas do comprimento de transmissão para a primeira fissura}}}\]

Fase de fissuração estabilizada

Depois de exceder aproximadamente 1,3 vezes a força crítica na zona de tração, não se formam novas fendas, o número de fendas no elemento é estabilizado e apenas a largura das fendas existentes aumenta com o carregamento adicional (fase número 3 na Fig. 1).

\[ \textsf{\textit{\footnotesize{Fig. 5 Tensões do betão e da armadura na fase de fendilhação estabilizada}}}\]

A largura da fenda durante o desenvolvimento estável pode ser calculada como:

\[{{w}_{k}}={{s}_{r,\max }}\left( {{\varepsilon }_{sm}}-{{\varepsilon }_{cm}} \right)\]

\[ \textsf{\textit{\footnotesize{Fig. 6 Fissuração estabilizada}}}\]

Força de tração crítica

O cálculo é baseado no modelo de corda de tração (TCM). A consideração básica é calcular a capacidade última de uma faixa de betão armado formada por um varão de armadura de área_As,eff rodeado por uma área efectiva de betão de tração_Ac,eff, que é capaz de resistir à tensão de tração até que a resistência à tração fct_,eff seja excedida (normalmente consideramos _fctm). Assumindo uma ligação perfeita entre a armadura e o betão, podemos considerar que até à ocorrência da primeira fissura, a remodelação da armadura e do betão envolvente é idêntica. Assim, a força máxima na faixa de tração imediatamente antes da primeira fissura_Nr pode ser determinada:

\[{{N}_{r}}={{A}_{c,eff}}\cdot {{f}_{ctm}}+{{A}_{s,eff}}\cdot {{\sigma }_{s}}\]

Introduzindo a substituição

\[{{\alpha }_{e}}={}^{{{E}_{s}}}/{}_{{{E}_{cm}}};{{\rho }_{p,eff}}={}^{{{A}_{s,eff}}}/{}_{{{A}_{c,eff}}}\]

obtemos:

\[{{N}_{r}}={{A}_{c,eff}}\cdot {{f}_{ctm}}\cdot \left( 1+{{\alpha }_{e}}\cdot {{\rho }_{p,eff}} \right)\]

Logo após a formação da primeira fenda, toda a força_Nr é transferida pela armadura e, portanto, a tensão na armadura que passa pela fenda recém-formada pode ser calculada como:

\[{{\sigma }_{sr}}=\frac{{{f}_{ctm}}}{{{\rho }_{p,eff}}}}\cdot \left( 1+{{\alpha }_{e}}\cdot {{\rho }_{p,eff}} \right)\Rightarrow {{\varepsilon }_{sr}}=\frac{{{f}_{ctm}}}{{{E}_{s}}\cdot {{\rho }_{p,eff}}}\cdot \left( 1+{{\alpha }_{e}}\cdot {{\rho }_{p,eff}} \right)\]

Cálculo da largura da fenda de acordo com EC 1992-1-1

A seguinte equação é utilizada para calcular a largura das fendas em elementos de betão armado:

\[{{w}_{k}}={{s}_{r,\max }}\left( {{\varepsilon }_{sm}}-{{\varepsilon }_{cm}} \right)\]

_sr,max. . . espaçamento máximo entre fissuras

_εsm . . . . a deformação média da armadura a partir da combinação de cargas, incluindo os efeitos da rigidez à tração.

_εcm . . . . deformação média do betão entre fissuras

Cálculo da diferença de deformação

A diferença de deformação da armadura e do betão entre fissuras pode ser obtida a partir da equação:

\[{{\varepsilon }_{sm}}-{{\varepsilon }_{cm}}=\frac{{{\sigma }_{s}}-{{k}_{t}}\cdot \frac{{{f}_{ct,eff}}}}{{{\rho }_{p,eff}}\cdot \left( 1+{{\alpha }_{e}}\cdot {{\rho }_{p,eff}} \right)\,}{{{E}_{s}}}\ge 0,6\frac{{{\sigma }_{s}}}{{{E}_{s}}}\]

σs_. . . . a tensão na armadura na fenda a partir da combinação de cargas em consideração

_{kt .} . . . um coeficiente empírico que tem em conta a deformação média, dependente da duração da carga. Pode assumir valores de 0,6 para análises a curto prazo. Para a análise a longo prazo, a redução da rigidez do compósito para cerca de 70% é tida em conta, pelo que o seu valor é 0,4, que inclui a taxa de degradação da coesão entre a armadura e o betão devido ao tempo.

_αe. . . . o rácio efetivo dos módulos elásticos

\[{{\alpha }_{e}}={}^{{{E}_{s}}}/{}_{{{E}_{cm}}}\]

_ςp,eff. . . . nível efetivo de reforço

\[{{\rho }_{p,eff}}={}^{\left( {{A}_{s,eff}}+{{\xi }^{2}_{1}}A_{p}^{\acute{\ }} \right)}/{}_{{{A}_{c,eff}}}\]

_Ac,eff. . . . a área efectiva do betão sob tração que envolve a armadura (determinação de_Ac,eff abaixo)

_As,eff. . . . a área da armadura ligada localizada na área de_Ac,eff

_Ap' . . . . é a área dos tendões pré ou pós-tensionados dentro de_Ac,eff

_ξ1. . . . . é o rácio ajustado da resistência da ligação, tendo em conta os diferentes diâmetros do aço de pré-esforço e de reforço:

\[{{\xi }_{1}}=\sqrt{\xi \,\cdot \,\frac{{{\phi }_{s}}}{{{\phi }_{p}}}}\]

ξ . . . o rácio da resistência da ligação entre o aço de pré-esforço e o aço de reforço (Quadro 6.2)

_ϕs. . . maior diâmetro da barra de aço de reforço

_ϕp. . . o diâmetro ou diâmetro equivalente do aço de pré-esforço

Para feixes,_Ap é a área da armadura no tendão

\[{{\phi }_{p}}=1,6\sqrt{{{A}_{p}}}\]

Para fios simples de sete fios, em que _φfio é o diâmetro do fio

\[{{\phi }_{p}}=1,75\,\,{{\phi }_{wire}}\]

Para cordões simples de três fios em que _φfio é o diâmetro do fio

\[{{\phi }_{p}}=1,20\,\,{{\phi }_{wire}}\]

Se apenas a armadura de pré-esforço for utilizada para evitar a fendilhação, então deve ser considerado o seguinte.

\[{{\xi }_{1}}=\sqrt{\xi \,}\]

Em elementos pré-esforçados, não é necessária uma área mínima de armadura ligada, desde que, sob a combinação caraterística de carga e o valor caraterístico da força de pré-esforço, a tensão de tração em qualquer fibra não seja superior à resistência à tração do betão, fct_,eff. (ver EN 1992-1-1 cap. 7.3.2 para mais pormenores)

A área efectiva do betão em tração

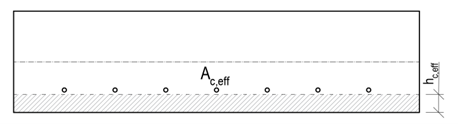
Um passo importante mas simultaneamente o mais complicado do cálculo é a determinação da área efectiva do betão à tração que envolve a armadura. Tanto o Eurocódigo como o Código Modelo consideram modos simples de carregamento, onde o elemento de betão armado é carregado por flexão uniaxial ou tensão. O valor da altura efectiva é determinado como:

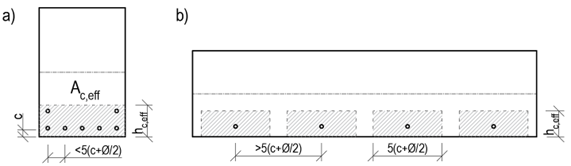
\[{{h}_{c,eff}}=\min \left\{ 2,5\left( h-d \right);\frac{\left( h-x \right)}{3};{}^{h}/{}_{2} \right\}\]

\[ \textsf{\textit{\footnotesize{Fig. 6 Determinação de Ac,eff para barras fletidas (esquerda) e barras em tração (direita)}}}\]

Normalmente, o valor hc_,eff = 2,5 (h-d) é crítico. Para elementos tensionados, o limite superior é h/2, enquanto para elementos dobrados é (h-x)/3. No entanto, a área_Ac,eff também é limitada pela largura determinada a partir da equação 5(c+ϕ/2). Se o espaçamento das armaduras for superior a 5(c+ϕ/2), então a área efetiva do betão tensionado de largura 5(c+ϕ/2) é considerada para as barras individuais.

\[ \textsf{\textit{\footnotesize{Fig. 9 Determinação de Ac,eff com base no espaçamento da armadura}}\]

Distância máxima de fendilhação

Ao calcular a distância máxima de fendilhação_sr,max, podem ocorrer dois casos:

• A distância axial da armadura ligada não excede uma distância de 5(c+ϕ/2) - Fig. 9a
• A distância axial das armaduras ligadas é superior a 5(c+ϕ/2) - Fig. 9b

O cálculo da distância máxima de fendilhação_sr,max para o caso de as distâncias axiais das armaduras não excederem o valor 5(c+ϕ/2) é definido da seguinte forma:

\[{{s}_{r,\max }}={{{k}_{3}}c+{{{k}_{1}}{{k}_{2}}{{{k}_{4}}\frac{\phi }{{{\rho }_{p,eff}}}\]

c . _. . . . valor do recobrimento do betão em mm. Uma vez que o valor do recobrimento pode ser diferente para a armadura de borda para as bordas horizontais e verticais, recomenda-se considerar o valor máximo de recobrimento encontrado para a armadura em consideração.

_ϕ . . . . diâmetro da armadura ligada. No caso de diâmetros de armadura diferentes, o diâmetro equivalente deve ser calculado de acordo com a Equação 7.12 da EN 1992-1-1.

\[{{\phi }_{eq}}=\frac{{{n}_{1}}\phi _{1}^{2}+{{n}_{2}}\phi _{2}^{2}}{{{n}_{1}}{{\phi }_{1}}+{{n}_{2}}{{\phi }_{2}}\]

_k1. . . . é um coeficiente que tem em conta as propriedades de ligação da armadura ligada

• _k1 = 0,8 para varões de alta aderência
• _k1 = 1,6 para varões com uma superfície efetivamente plana (por exemplo, tendões de pré-esforço)

_k2. . . . é um coeficiente que tem em conta a distribuição das deformações

• _k2 = 1,0 para a flexão
• _k2 = 0,5 para a tração pura

Para casos de tensão excêntrica ou para áreas locais, devem ser utilizados valores intermédios de _k2 que podem ser calculados a partir da relação:

\[{{k}_{2}}=\frac{{{\varepsilon }_{1}}+{{\varepsilon }_{2}}}{2{{\varepsilon }_{1}}}\]

k3_. . . . coeficiente que expressa o comprimento da área próxima de uma fissura onde a ligação entre o betão e a armadura é quebrada. O valor recomendado do CE de base _k3 = 3,4 pode ser modificado pelo Anexo Nacional.

O coeficiente k4_. . . . exprime a relação entre a ligação e a resistência à tração do betão. O valor recomendado do CE de base k4 = 0,425 pode ser ajustado pelo Anexo Nacional.

O cálculo da distância máxima de fendilhação_sr,max para o caso de as distâncias axiais das armaduras excederem o valor 5(c+ϕ/2) é definido da seguinte forma:

\[{{s}_{r,\max }}=1,3\left( h-x \right)\]

Valores máximos de distância de fenda de acordo com a equação

\[{{s}_{r,\max }}=1,3\left( h-x \right)\]

devem ser sempre superiores aos valores determinados pela equação

\[{{s}_{r,\max }}={{k}_{3}}c+{{k}_{1}}{{k}_{2}}{{k}_{4}}}{\phi }/{{{\rho }_{p,eff}}}\;\]

caso contrário, recomenda-se que se considere a maior distância obtida a partir das equações acima. A equação para a deformação no betão/reforço não é modificada para o caso da grande distância axial do reforço. Em áreas com larguras de fendas controladas, a distância axial das armaduras individuais não deve ser superior a 5(c+ϕ/2).

Cálculo da largura da fenda implementado no RCS

Determinação da área efectiva_Ac,eff

Uma vez que não é tão simples determinar qual a armadura que pode ser considerada como armadura longitudinal resistente à fendilhação,_Ac,eff é determinada utilizando o seguinte processo iterativo.

• De todas as armaduras que actuam em tração, é determinado o centro de força de tração Cg_,s,1. A profundidade efectiva da armadura d é a distância entre Cg_,s, e a fibra de betão mais comprimida calculada na direção do momento fletor resultante. Ao mesmo tempo, são determinadas a posição do eixo neutro e a altura da área comprimida x para a secção fendilhada. Isto torna possível determinar a altura efectiva hc_,eff:

\[{{h}_{c,eff}}=\min \left\{ 2,5\left( h-d \right);\frac{\left( h-x \right)}{3};{}^{h}/{}_{2} \right\}\]

• Ao excluir todas as armaduras que se encontram fora de_Ac,eff,1, o novo centro da armadura Cg_,s,2 é determinado, juntamente com a nova profundidade efectiva da armadura d, a altura efectiva hc_,eff é determinada da mesma forma que no passo anterior, apenas com valores de entrada alterados.

Mais uma vez, é verificado se toda a armadura tensionada em consideração se encontra no_Ac,eff,2. Se esta condição for satisfeita, a iteração pode ser terminada e os valores de hc_,eff,2,_Ac,eff,2 e_As,eff,2 são apresentados como os valores resultantes no IDEA StatiCa RCS.

Casos possíveis de cálculo da largura da fenda

Em geral, podem ocorrer três casos no cálculo da largura da fenda:

• A armadura de tração encontra-se na região_Ac,eff, sendo a distância axial das armaduras individuais inferior a 5(c+ϕ/2). Então, as seguintes definições são utilizadas para o cálculo:

\[{{s}_{r,\max }}={{k}_{3}}c+{{{k}_{1}}{{k}_{2}}{{{k}_{4}}\frac{\phi }{{{\rho }_{p,eff}}}\]

\[{{\varepsilon }_{sm}}-{{\varepsilon }_{cm}}=\frac{{{\sigma }_{s}}-{{{k}_{t}}\,\cdot \,\frac{{{f}_{ct,eff}}}}{{{\rho }_{p,eff}}}\,\cdot \,\left( 1+,{{\alpha }_{e}}\cdot \,{{\rho }_{p,eff}} \right)\,\,}{{{E}_{s}}}\ge 0,6\frac{{{\sigma }_{s}}}{{{E}_{s}}}\]

• A armadura de tração encontra-se no_Ac,eff, com a distância axial das armaduras individuais a exceder a distância 5(c+ϕ/2). De seguida, são utilizadas as seguintes definições para o cálculo:

\[{{s}_{r,\max }}=1,3\left( h-x \right)\]

\[{{\varepsilon }_{sm}}-{{{\varepsilon }_{cm}}=\frac{{{\sigma }_{s}}-{{k}_{t}}\,\cdot \,\frac{{{f}_{ct,eff}}}}{{{\rho }_{p,eff}}}\,\cdot \,\left( 1+,{{\alpha }_{e}}\cdot \,{{\rho }_{p,eff}} \right)\,\,}{{{E}_{s}}}\ge 0,6\frac{{{\sigma }_{s}}}{{{E}_{s}}}\]

• A armadura de tração não se encontra no_Ac,eff (isto pode ser causado, por exemplo, por uma cobertura espessa).

Neste caso, não seria possível calcular a largura das fendas. Por isso, o cálculo da altura efectiva hc_,eff é modificado da seguinte forma:

\[{{h}_{c,eff}}=\min \left\{ 2,5\left( h-d \right);h/2 \right\}\]

Ao mesmo tempo, é apresentada a seguinte não conformidade:

A área efectiva de betão à tração que envolve a armadura ou os tendões de pré-esforço de profundidade hc_,eff, em que hc_,eff é o menor de 2,5(h - d) ou h/2. Considerando o valor como(h - x)/3, a armadura está fora da área efectiva do betão em tração, pelo que não seria possível calcular a largura da fenda de acordo com o ponto 7.3.4.