Métodos de controlo da capacidade de secção
Dois métodos bem conhecidos podem ser utilizados para verificar o estado limite último para elementos de betão 1D. O primeiro dá-nos a resistência última da secção transversal sob a forma de uma área de interação ou de um diagrama de interação (no caso de momento fletor numa direção).A capacidade da secção transversal pode ser determinada como o rácio entre as forças internas actuantes e as forças do estado limite. A segunda consiste em encontrar o equilíbrio numa secção transversal, onde procuramos o comportamento real da secção carregada, a utilização de materiais em termos de tensões e a perceção das vulnerabilidades da secção.
Pressupostos gerais de projeto e pressupostos de cálculo para o estado limite último
- A deformação ε na armadura e no betão deve ser assumida como diretamente proporcional à distância ao eixo neutro (as secções planas permanecem planas).
- A interação entre a armadura e o betão é assegurada pela interação entre o betão e a armadura sem deslizamento (a deformação ε suporta a deformação no betão e as fibras adjacentes são as mesmas).
- A resistência à tração do betão é negligenciada (todas as tensões de tração são transmitidas pela armadura).
- As tensões de compressão do betão na zona de compressão são calculadas em relação à deformação calculada a partir dos diagramas tensão-deformação.
- As tensões da armadura são calculadas em relação à deformação a partir dos diagramas tensão-deformação.
- Deformação compressiva do betão com um limite de deformação último εcu2 (diagrama parábola-retângulo para betão sob compressão) e εcu3 (relação bi-linear tensão-deformação),[2].
- A deformação de compressão da armadura é ilimitada no caso do ramo superior plástico horizontal, no caso do ramo superior plástico inclinado a deformação é limitada εud,[2].
- Um estado limite é considerado quando o estado de pelo menos um dos materiais excede a deformação limite última (se εu não for limitado, o betão comprimido é determinante).
\[ \textsf{\textit{\footnotesize{\qquad Strain stress.}}}\]
\[ \textsf{\textit{\footnotesize{\qquad Diagrama de dimensionamento tensão-deformação para aço de reforço com ramo superior inclinado.}}}\]
Diagrama de interação
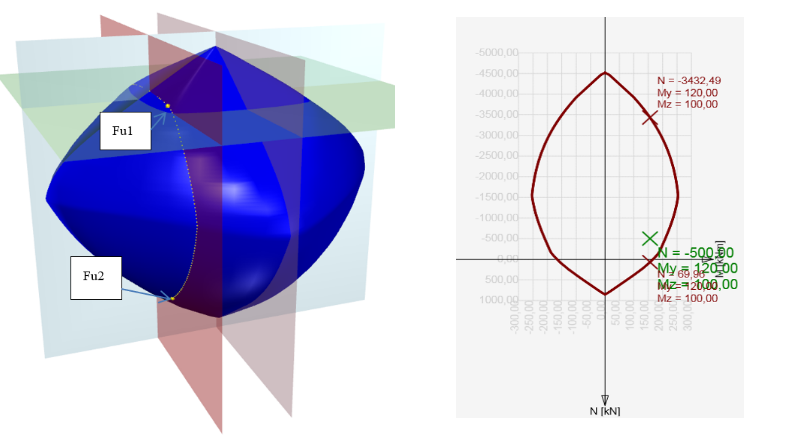
A primeira opção é verificar a secção através de uma superfície de interação (ou diagrama de interação). É fornecida uma explicação sobre uma amostra das superfícies de interação para a secção quadrada reforçada do exemplo na figura abaixo. Na superfície de interação estão localizados pontos que definem o estado limite último da secção examinada.A superfície de interação é desenhada a partir dos pontos (N, My, Mz), que são determinados pela integração de tensões na secção, que atingiu a tensão limite última num dos materiais.Para uma interação 3D, a superfície pode ser derivada de um diagrama de interação 2D, que é uma curva fechada, que corresponde à tensão de um eixo neutro constantemente rodado.
\[ \textsf{\textit{\footnotesize{\qquad Secção reforçada simétrica.}}}\]
\[ \textsf{\textit{\footnotesize{\qquad A superfície de interação mostra as condições de rotura para todos os casos de carga de força normal e momentos fletores.}}}\]
Para o caso de uma secção simétrica em torno do eixo y, o diagrama de interação é simétrico em torno do plano N-My. De forma idêntica, para o caso de uma secção simétrica em torno do eixo z, o diagrama de interação é simétrico em torno do plano N-Mz. A secção reforçada unilateral introduz uma forma achatada do diagrama de interação
\[ \textsf{\textit{\footnotesize{\qquad Secção reforçada simétrica simples.}}}\]
\[ \textsf{\textit{\footnotesize{\qquad Superfície de interação para secção com armadura simétrica simples.}}}\]
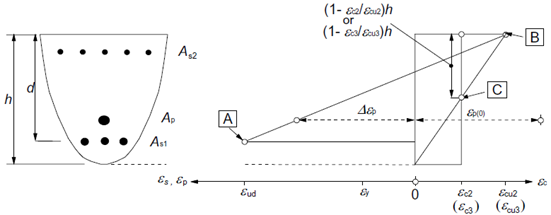
Os pontos que definem o estado limite último são recebidos da integração de tensões. A figura abaixo apresenta a deformação no estado limite último.
Distribuições de deformação no estado limite último (retirado de [2]).
O diagrama de interação mostra a rotura da secção transversal sob força normal e momentos flectores.[1]
Respeitando o problema do diagrama 2D (curva fechada colocada na superfície de interação), podemos descobrir que o plano de deformação passa pelo eixo neutro e pelo ponto crítico [y, z, ε], que é considerado como ponto crítico R. O ponto [y, z] define um ponto na secção transversal com o valor da deformação ε no estado limite último. A inclinação do eixo neutro é constante para todos os pontos do diagrama 2D.
No caso de a tensão de compressão no betão ser crítica para o dimensionamento, o ponto R corresponde à fibra de betão mais comprimida ou ao ponto limite C. No entanto, isto só pode ser aplicado se essa secção for feita de um tipo de betão - não como uma secção transversal mista.
No caso de a tensão de tração na armadura ser crítica para o dimensionamento (a deformação εud é excedida no estado limite último para um ou mais varões), deve ser cumprida a condição de que, para o plano de deformação dado, o valor εud não é excedido em nenhum outro varão.
\[ \textsf{\textit{\footnotesize{\qquad Utilização óptima do material da secção}}\]
\[ \textsf{\textit{\footnotesize{\qquad Posições do plano de deformação caraterístico calculadas para efeitos do diagrama de interação.}}\]
A imagem acima mostra que o diagrama pode ser dividido em duas partes: a parte em que a falha é causada por uma força de tração e a parte que falha por uma força de compressão.Os pontos limite correspondem ao caso acima, onde também se pode ver a inclinação extrema do plano de deformação.Ao desenhar um diagrama de interação, a inclinação do plano de deformação de uma secção transversal está a mudar neste intervalo, enquanto procuramos o ponto R (ver acima). Com base nesse plano definido, efectuamos a integração para obter a tensão no estado limite último.
Secção transversal sujeita a força axial e verificação do momento fletor
A verificação de uma secção transversal sujeita a força axial e momento fletor baseia-se em provar que as tensões verificadas (combinação Nd,Myd, Mzd) estão localizadas dentro ou na área de interação da superfície. O exemplo seguinte demonstra a verificação de uma secção retangular sujeita a forças Nd= -500 kN,Myd = 120 kNm, Mzd = 100 kNm.
Método NuMuMu
Para definir a resistência de uma secção transversal, assumimos alterações proporcionais em todas as componentes da força interna (a excentricidade da força normal permanece constante) até que a superfície interactiva tenha sido desenvolvida.A alteração das forças internas envolvidas pode ser interpretada como um movimento ao longo de uma linhaque liga o sistema de coordenadas inicial (0,0,0) e o ponto definido pelas forças internas (NEd,MEd,y,MEd,z).As duas intersecções desta linha com a superfície de interação, que podem ser encontradas, representam dois conjuntos de forças no estado limite último. Em cada intersecção, o programa determina três forças no estado limite: a resistência da força axial de cálculoNRd e os correspondentes momentos de resistência de cálculoMRdy,MRdz.
Método NuMM
Para definir a resistência da secção transversal, assumimos uma força normal constante (que é igual à força normal de cálculo atuante) e alterações proporcionais nos momentos fletores até que a superfície interactiva tenha sido desenvolvida.A variação das forças internas envolvidas pode ser interpretada como um movimento num plano horizontal ao longo da linha que liga o ponto (NEd,0,0) e o ponto definido pelas forças internas actuantes (NEd,MEd,y,MEd,z).As duas intersecções desta linha com a superfície de interação, que pode ser encontrada, representam dois conjuntos de forças no estado limite último. Em cada intersecção, o programa determina três forças no estado limite: os momentos resistentes de dimensionamentoMRdy,MRdz e a força normal de dimensionamento (correspondente) atuanteNEd.
Método NMuMu
Para definir a resistência da secção, assumimos uma força normal constante (que é igual à força normal de cálculo atuante) e alterações proporcionais nos momentos fletores até que a superfície interactiva tenha sido desenvolvida.A alteração das forças internas envolvidas pode ser interpretada como um movimento num plano horizontal ao longo da linha que liga o ponto (NEd,0,0) e o ponto definido pelas forças internas actuantes (NEd,MEd,y,MEd,z).As duas intersecções desta linha com a superfície de interação, que podem ser encontradas, representam dois conjuntos de forças no estado limite último. Em cada intersecção, o programa determina três forças no estado limite: os momentos resistentes de dimensionamentoMRdy,MRdz e a (correspondente) força normal de dimensionamento atuanteNEd.
Determinação da resposta da secção
Outra possibilidade de verificar a secção transversal é encontrar a resposta da secção transversal (ou seja, a distribuição de deformação e tensão das forças internas actuantes). Este método também é conhecido como o método da deformação limite.O nível de tensões actuantes em cada fibra (no caso de flexão plana em cada camada) emCada barra reforçada é calculada em função da tensão do diagrama tensão-deformação do material.
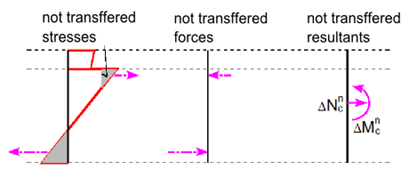
A determinação da resposta da secção transversal é calculada utilizando o método numérico especificado em[6]. O princípio consiste no aumento gradual da carga da secção através dos componentes desequilibrados das forças não transferidas, que são obtidos através da integração da tensão sobre a secção utilizando diagramas tensão-deformação.Se o valor da tensão puder ser encontrado para a deformação no diagrama tensão-deformação, ver Figura abaixo (a), a tensão calculada está correta, assumindo um material elástico linear.Nos casos (b) e (c), a tensão para um cálculo linear atinge valores irrealistas, e parte (b) ou todo o valor (c) não pode ser transmitido pelo material. Integrando as tensões não transferidas, obtemos forças internas não transferidas, e as suas resultantes devem ser adicionadas às forças internas de cargas variáveis.
Tensões não transferidas em diagramas tensão-deformação [4].
Forças internas não transferidas.[4]
Este método de cálculo requer a utilização de métodos numéricos para integrar a tensão sobre a área da secção transversal e para a análise não linear das equações de equilíbrio na secção. A iteração é terminada no momento em que os critérios de convergência são cumpridos.
\[\frac{{F_e} - {F_i}}}{{{F_e}}} \le max\left\{ {e,d} \right\}\]
em que
Fe é a carga da secção,
Fi é a resposta da secção (forças internas calculadas na base do plano de deformação).
Se a é o valor aproximado (aproximado) e b é o valor exato (verdadeiro), então o desvio absoluto é dado pela seguinte equação.
\[e = \left| {b - a} \right|\]
O desvio relativo é dado pela seguinte fórmula:
\[d = \left| {\frac{{b - a}}}{b}} \right|\]
Na maioria dos programas, é possível definir estes critérios de convergência (os valores predefinidos são 1%como erro relativo, 100 N, 100 Nm como erro absoluto da força normal e dos momentos).
Assim, se tivermos a entrada de N = 0 kN, My = 100 kNm, Mz= 0 kNm e as forças integradas após a iteração N = - 0.07 kN, My = 100,5 kNm, Mz = 0,02 kNm, a avaliação será a seguinte. Respeitando o facto de N e Mz serem iguais a 0, pode ser feita uma comparação com o desvio absoluto:
O valor da força normal 100N> | 70 | N
O valor do momento fletor Mz 100Nm> | 20 | Nm
O valor do momento fletor My
\[d = \left| {\frac{{b - a}}{b}} \direita| = \frac{{100 - 100,5}}{{{100}} = 0,005\; < 0,01\]
Verificação da secção transversal pela resposta
No caso de encontrar um equilíbrio na secção, a deformação plana é conhecida.A partir da deformação plana, podemos calcular a deformação em qualquer parte da secção e, em seguida, a tensão ou as forças internas nas barras de reforço, na secção ou nas suas partes utilizando diagramas de tensão-deformação dos materiais. Os valores de tensão e deformação calculados são comparados com o valor de deformação limite dos diagramas de tensão-deformação dos materiais utilizados.
A vantagem deste método é que obtemos uma imagem completa dos valores de tensão e deformação na secção das forças internas que actuam na secção transversal.