O diagrama N-M-κ mostra a curvatura de um elemento (rigidez à flexão) em função de um momento fletor e de uma força normal aplicados. Existem três tipos de diagramas N-M-κ:
- curto prazo,
- longo prazo
- ULS.
Estes diagramas diferem nos tipos de diagramas tensão-deformação utilizados para o cálculo (explicados abaixo).
O cálculo da rigidez para estados caraterísticos selecionados da secção transversal é utilizado para determinar o diagrama N-M-κ. Em geral, pode ser qualquer estado da secção transversal a partir do qual a resposta é calculada e a partir do qual a rigidez à flexão e a curvatura são derivadas. No IDEA RCS, consideramos quatro pontos caraterísticos (Mr,Mc,Ms eMu)
Mr - o momento de fendilhação
A secção transversal é sujeita a uma força normal definida pelo utilizador e o plano de deformação começa a rodar (na direção do momento fletor especificado) até que a resistência à tração máxima do betão seja atingida numa fibra de betão (para o grau de betão C30/37, isto é fctm = 2,896 MPa). Para o cálculo, é utilizado um diagrama de tensão-deformação bilinear com um ramo plástico horizontal tanto para a armadura como para o betão.
Mc - o momento fletor quando a resistência à compressão do betão é atingida
A partir do passo anterior, é identificada a fibra de betão mais utilizada na compressão. Para esta fibra, é definida a deformação na resistência máxima do betão (fck/Ecm para curto prazo, fck/Eceff para longo prazo e fcd/Ecm para o diagrama ULS). Com base na força normal definida e na direção do momento fletor, o processo de iteração para encontrar o plano de deformação é executado para encontrar um equilíbrio entre a resposta da secção transversal e a força normal definida. É utilizado para o cálculo um diagrama tensão-deformação bilinear com um ramo plástico horizontal para a armadura e o betão.
Ms - o momento fletor quando é atingida a tensão de cedência na barra de armadura mais utilizada
Outro ponto caraterístico do diagrama N-M-κ é o estado de tensão da secção quando a tensão de cedência no varão de armadura mais utilizado é atingida (a deformação do varão é igual a fyk/Es para os diagramas de curto e longo prazo, fyd/Es para o diagrama ULS). O processo de iteração encontra um equilíbrio de forças normais na secção transversal rodando o plano de deformação em torno do ponto especificado pela posição do varão de armadura mais utilizado. Para o cálculo, é utilizado um diagrama de tensão-deformação bilinear com um ramo plástico horizontal para a armadura e o betão.
Mu - o momento fletor no estado limite último
Esta é a capacidade de carga última de uma secção transversal em flexão, quando a secção transversal está sujeita a uma força normal de projeto definida Ned. Para o cálculo da capacidade da secção transversal, assume-se que a resistência à compressão na fibra mais utilizada do betão e a resistência à tração no varão de armadura mais utilizado são atingidas (deformação máxima para o betão εcu = 0,1 e para a armadura εs,max = 0,5. Para o cálculo, é utilizado um diagrama bilinear tensão-deformação com um ramo plástico horizontal para a armadura e um diagrama parábola-retângulo para o betão.
A rigidez e a curvatura resultantes devido à combinação definida pelo utilizador da força normal e do momento fletor ( Md) são então calculadas utilizando a interpolação linear dos pontos caraterísticos individuais do diagrama N-M-κ.
Cálculo de rigidezes e curvaturas
As rigidezes e curvaturas para cada estado de tensão na secção transversal (Mr,Mc,Ms ouMu) são calculadas diretamente a partir da rotação do plano de deformação.
\[E{{A}_{x}}=\frac{N}{{{\varepsilon }_{x}}}\]
EAx. . . rigidez axial do elemento
N . . . . a força normal especificada
εx. . . deformação axial no centro de gravidade da secção transversal de betão
\[E{{I}_{y}}=\frac{M}{\kappa }\]
EIy. . . rigidez à flexão do elemento
M . . . o momento fletor calculadoMr,Mc,Ms ouMu
κ . . . . a curvatura do elemento, calculada como a tangente do ângulo entre o plano da deformação e o eixo longitudinal do elemento
Exemplo prático
Uma secção transversal de betão (betão de grau C30/37) é reforçada com armadura ϕ32 (grau B500B). A combinação quase-permanente definida é N = -730 kN eMy = 557 kNm.
O plano de deformação para o ponto caraterísticoMs é determinado pelo IDEA RCS da seguinte forma:
\[E{{A}_{x}}=\frac{N}{{{\varepsilon }_{x}}}=\frac{730}{6,9471\cdot {{10}^{-4}}}=1050,798MN\]
\[\kappa =\frac{28,4386\cdot {{10}^{-4}}}}{0,463}=61,422\cdot {{10}^{-4}}{{{m}^{-1}}\]
\[E{{I}_{y}}=\frac{{{M}_{s}}}{\kappa }=\frac{2277,4}{61,422\cdot {{10}^{-4}}}=370,776MN{{m}^{2}}\]
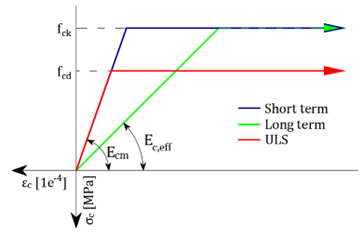
Diagramas de tensão-deformação utilizados para o cálculo
Reforço -Mr,Mc,Ms eMu
Betão -Mr,Mc,Ms
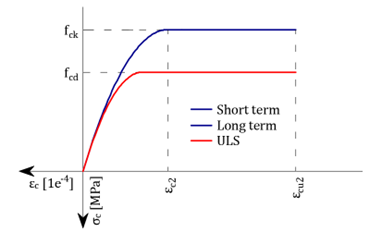
Betão -Mu