De inbreng van interne krachten
De invoer van interne krachten van 2D-elementen hangt af van het type 2D-element:
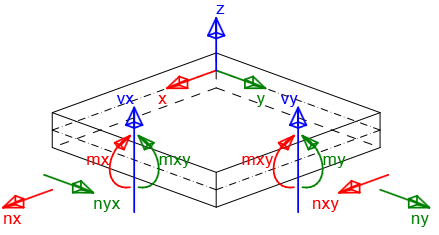
- Shell-vloerplaat - membraankrachten (nx, ny en nxy), buigmomenten (mx,my en mxy) en dwarskrachten (vx en vy) kunnen worden ingevoerd.
- Shell-wand - membraankrachten (nx, ny en nxy), buigmomenten (mx,my en mxy) en dwarskrachten (vx en vy) kunnen worden ingevoerd.
- Vloerplaat - enkel buigmomenten (mx,my en mxy) en dwarskrachten (vx en vy) kunnen ingevoerd worden
- Wand - alleen membraankrachten (nx, ny en nxy) kunnen ingevoerd worden
- Diepe balk - alleen membraankrachten (nx, ny en nxy) kunnen ingevoerd worden
| Beschrijving | |
| mx(y) | Buigmoment in de richting van de x (y)-as. Een positieve waarde veroorzaakt spanning aan de onderkant van een 2D-element. |
| mxy(yx) | Torsiemoment om de y (x)-as dat inwerkt op de rand evenwijdig aan de x (y)-as. Positieve waarde veroorzaakt schuifspanning aan het ondervlak van een 2D-element. Omdat in elk punt van de 2D-element stelling de gelijkheid van horizontale schuifspanningen geldt, zijn torsiemomenten mxy = myx ook gelijk in elk punt van het 2D-element. Daarom wordt alleen de waarde mxy in het programma ingevoerd. |
| nx(y) | Normaalkracht in de richting van de x (y)-as. Positieve waarde werkt in de richting van de x(y)-as en veroorzaakt spanning in de doorsnede. |
| nxy(yx) | Normaalkracht die werkt in het middenvlak in de richting van y(x)-as op rand parallel aan x(y)-as. Positieve waarde werkt in de richting van de x(y)-as. Omdat in elk punt van de 2D-element stelling de gelijkheid van horizontale schuifspanningen geldt, zijn normaalkrachten nxy = nyx ook gelijk in elk punt van het 2D-element. Daarom wordt alleen de waarde nxy in het programma ingevoerd. |
| vx(y) | Dwarskracht die loodrecht op het middenvlak werkt op rand evenwijdig aan x(y)-as. Positieve waarde werkt in de richting van de z-as. |
Tekenconventie van interne krachten.
De volgende typen combinaties moeten gedefinieerd worden voor controles:
- Uiterste grenstoestand/Accidenteel - interne krachtcomponenten gedefinieerd voor dit type combinaties worden gebruikt voor UGT controles van 2D elementen:
- Capaciteit N-M-M
- Analyse N-M-M
- Interactie
en de controle van detailleringseisen:
- Karakteristiek - interne krachtcomponenten gedefinieerd voor dit type combinatie worden gebruikt voor controle van spanningsbeperking (BGT)
- Quasi-permanent - interne krachtcomponenten gedefinieerd voor dit type combinatie worden gebruikt voor controle van scheurwijdte (BGT)
| Opmerking: |
| Interne krachtcomponenten Vx en Vy hoeven niet ingevoerd te worden voor combinatietypes Karakteristiek en Quasi-permanent, omdat deze waarden niet gebruikt worden bij controles. |
De richting van de controle bepalen
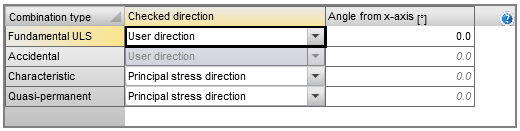
Voor een goede controle van het 2D-element moet de richting van de controle worden bepaald. De richting van de controle kan voor elk combinatietype afzonderlijk worden ingevoerd met behulp van de volgende twee methoden:
- Door gebruiker gedefinieerde richting - de gebruiker definieert de controlerichting als een hoek ten opzichte van de x-as in het vlak van het 2D-element. Deze optie is standaard ingesteld voor combinatietype UGT en de voorgedefinieerde waarde van de hoek is 0 graden. Controles worden uitgevoerd in de volgende richtingen:
- Gedefinieerde richting
- Richting loodrecht op gedefinieerde richting
- Richting van de drukdiagonaal aan de bovenkant
- Richting van de drukdiagonaal aan het onderoppervlak
- Richting van de hoofdspanningen - de controlerichting wordt automatisch berekend als de richting van de hoofdspanningen aan het boven- en ondervlak van het 2D-element. Deze optie is standaard ingesteld voor combinatietypes Karakteristiek en Quasi-permanent. Controles worden uitgevoerd in de volgende richtingen:
- Richting van de hoofdspanningen aan het onderoppervlak
- Richting loodrecht op de richting van de hoofdspanningen aan het ondervlak
- Richting van de drukdiagonaal aan het onderoppervlak
- Richting van de hoofdspanningen aan het bovenoppervlak
- Richting loodrecht op de richting van de hoofdspanningen aan het bovenoppervlak
- Richting van de drukdiagonaal aan het bovenoppervlak
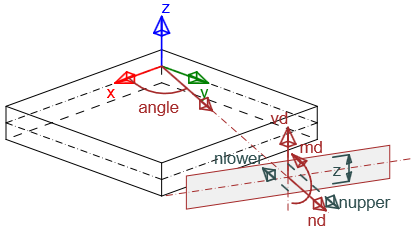
Berekende inwendige krachten in de ingaande richting volgens de theorie van Baumann.
Analyse van controlerichting voor uiterste grenstoestand
Analyse 1
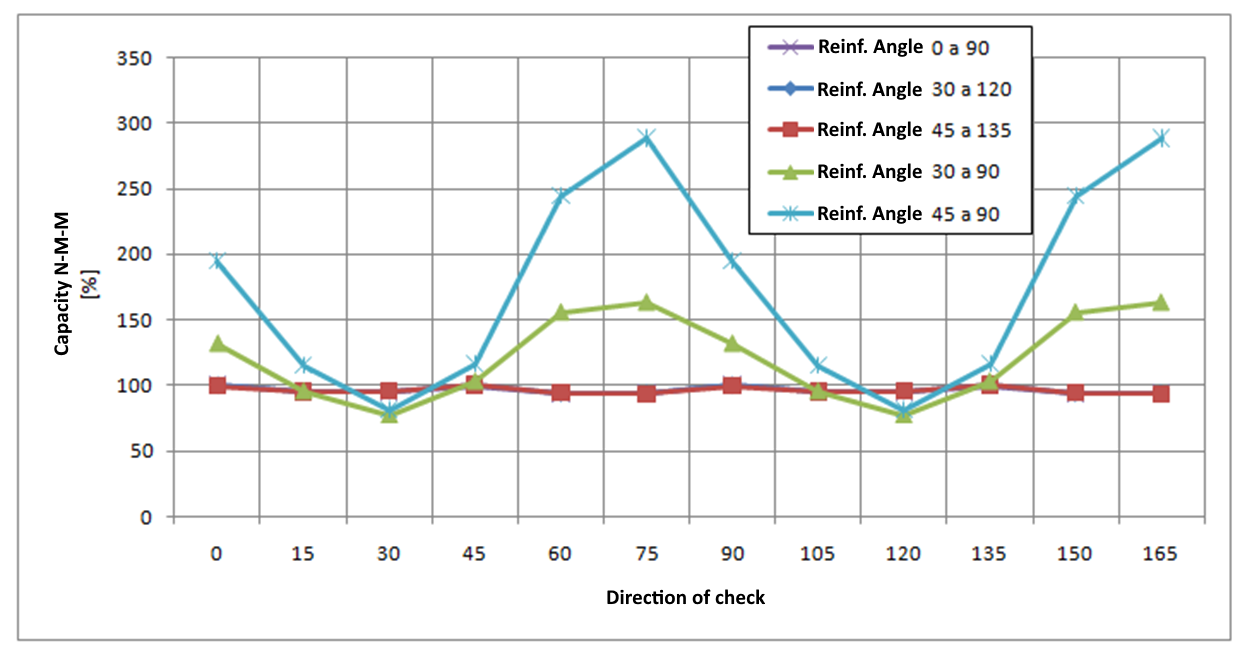
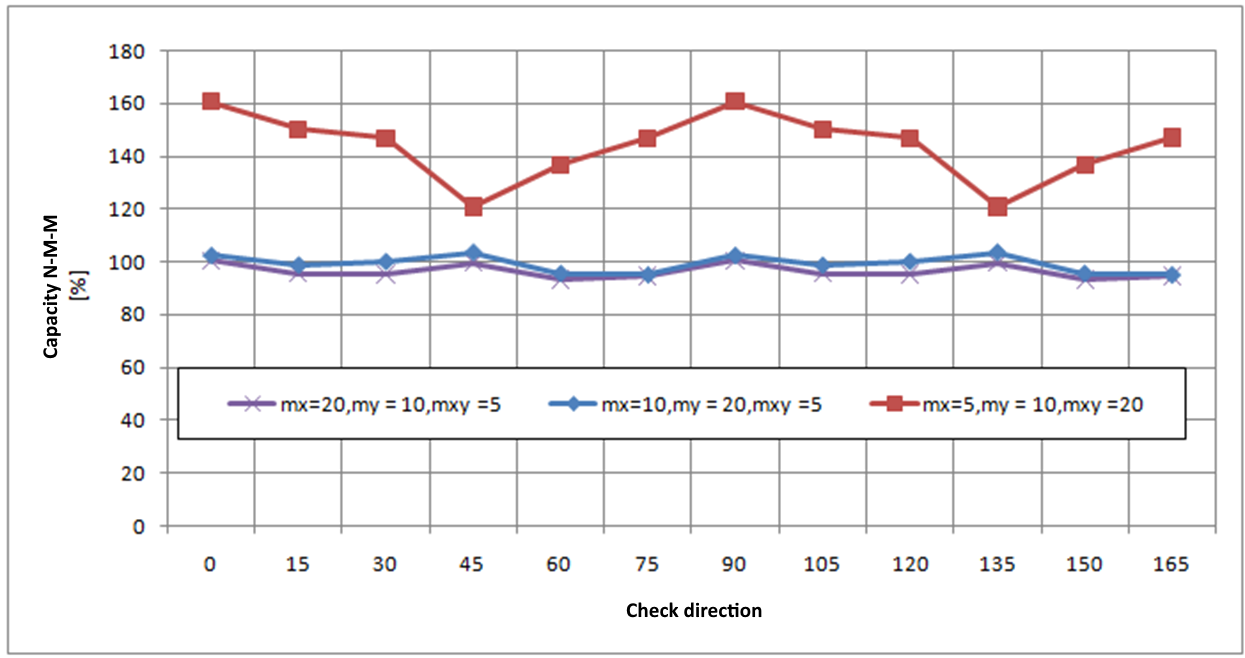
Voor een 2D-element dat alleen wordt belast door buigmomenten (mx = 20 kNm/m, my = 10 kNm/m, mxy = 5 kNm/m ) met de hoek van wapening en hoek van controlerichting gewijzigd voor de uiterste grenstoestand - de resultaten worden weergegeven in de volgende grafiek:
De analyse impliceert:
- Als wapeningsstaven loodrecht op elkaar staan, zijn de controleresultaten vergelijkbaar voor verschillende hoeken van de controlerichting, ze zijn niet afhankelijk van de gedefinieerde wapeningshoek en de maximale waarde van de controle wordt gevonden voor hoeken 0, 45 en 90 graden. Deze controle kan dus worden uitgevoerd voor een vooraf gedefinieerde richting van een controlehoek van 0 graden.
- Als wapeningsstaven niet loodrecht op elkaar staan, verschillen de resultaten van de controles aanzienlijk en wordt de maximale controlewaarde ongeveer bereikt in de richting die overeenkomt met de richting van de gemiddelde wapening. Het wordt dus aanbevolen om de vooraf gedefinieerde controlerichting te wijzigen of controles in meer richtingen uit te voeren in gevallen waarin wapeningsstaven niet loodrecht op elkaar staan.
Analyse 2
Voor de orthogonale wapening zijn de waarden van de buigmomenten en de hoek gewijzigd voor de UGT code-check. De resultaten worden weergegeven in de grafiek:
De analyse geeft aan dat zelfs voor verschillende waarden van buigende momenten de maximale waarde van de controle van de uiterste grenstoestand wordt gevonden voor controle richtingen 0, 45 en 90 graden. De controle kan dus worden uitgevoerd voor een vooraf gedefinieerde controlehoek van 0 graden. Een gelijkaardige conclusie geldt voor 2D-elementen die enkel belast worden door normaalkracht of belast worden door normaalkracht gecombineerd met buigmomenten.
Herberekening van interne krachten naar kijkrichtingen
De gedefinieerde interne krachten worden herberekend naar de controle richtingen met behulp van de Baumann transformatie formule, beschreven in Baumann, Th. : "Zur Frage der Netzbewehrung von Flächentragwerken". In : Der Bauingenieur 47 (1972), Berlijn 1975. De berekeningsprocedure is als volgt:
- Berekening van normaalkrachten aan beide oppervlakken van het 2D-element
- Berekening van de hoofdkrachten aan beide oppervlakken van het 2D-element
- Berekening van herberekende krachten voor elk oppervlak naar de gedefinieerde ruitrichting
- Berekening van herberekende krachten voor elk oppervlak naar het middelpunt
- Herberekening van dwarskrachten naar de gedefinieerde controlerichting
Berekening van normaalkrachten op beide oppervlakken van het 2D-element
De gedefinieerde interne krachten worden herberekend naar beide oppervlakken met behulp van de volgende formules:
\[{{n}_{x,low\left( upp \right)}}=\frac{{{n}_{x}}}{2}+\left( - \right)\frac{{{m}_{x}}}{z}\]
\[{{n}_{y,low\left( upp \right)}}=\frac{{{n}_{y}}}{2}+\left( - \right)\frac{{{m}_{y}}}{z}\]
\[~~~~~{{n}_{xy,low\left( upp \right)}}=\frac{{{n}_{xy}}}{2}+\left( - \right)\frac{{{m}_{xy}}}{z}\]
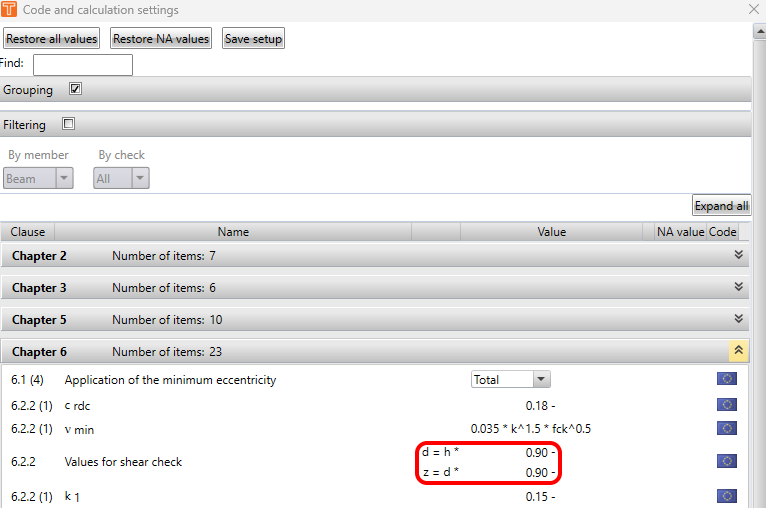
De hefboomarm van interne krachten (z) moet worden bepaald voor de herberekening van interne krachten. De hefboomarm van inwendige krachten wordt bepaald uit de methode van grensrek bij belasting door het hoofdbuigmoment in richtingen van de hoofdmomenten m1 aan beide oppervlakken. Als de hoofdmomenten gelijk zijn aan nul of als het evenwicht niet wordt gevonden in de richting van de hoofdmomenten, wordt de hefboomarm van de interne krachten bepaald volgens de formule:
\[z=x\cdot d\]
| Beschrijving | |
| x | De coëfficiënt voor de berekening van de interne krachten arm is gedefinieerd in de National Code Setup. |
| d | De effectieve hoogte van de doorsnede, afzonderlijk berekend voor het boven- en ondervlak van het 2D-element. Voor het ondervlak is het een afstand van het middelpunt van wapeningsstaven aan het ondervlak tot de bovenrand van de doorsnede. Voor het bovenvlak is het een afstand van het zwaartepunt van de wapeningsstaven op het bovenvlak tot de onderrand van de doorsnede. |
| Opmerking: |
| De arm van interne krachten kan geverifieerd worden in de Response N-M-M check. Alleen de buigmomenten moeten worden ingevoerd en de controlerichting moet overeenkomen met de richting van het hoofdmoment. |
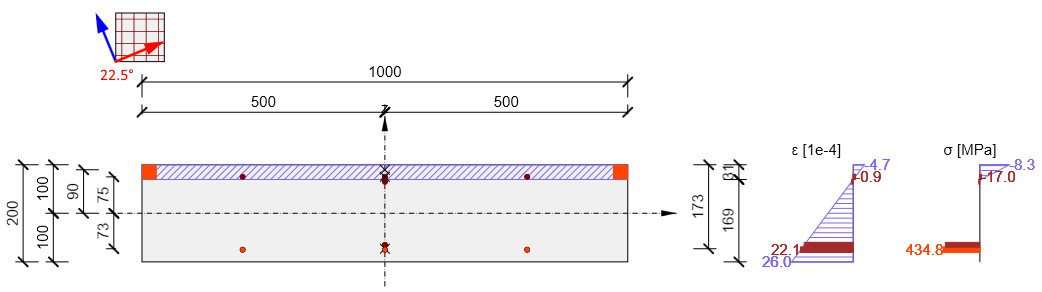
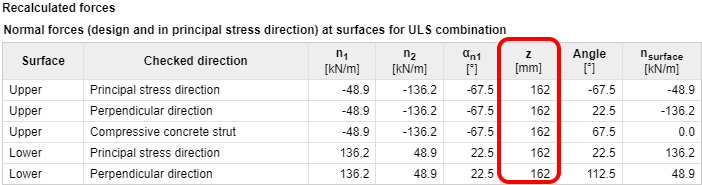
In het volgende diagram wordt een controle van de hefboomarm van de interne krachten weergegeven voor buigmomenten mx = 20 kNm/m, my = 10 kNm/m, mxy = 5 kNm/m. De richting van de hoofdmomenten is berekend als αm1 = 22,5 graden en de respons van de doorsnede is berekend om de hefboomarm van de interne krachten te bepalen.
| Opmerking: |
| Interne kracht hefboomarmen voor herberekening van interne krachten in de richting van de controle en interne kracht hefboomarmen voor controles kunnen verschillend zijn, omdat de interne kracht hefboomarm voor herberekening wordt bepaald op een doorsnede belast door hoofdmomenten in de richting van hoofdmomenten, en de interne kracht hefboomarm voor de controle wordt bepaald op een doorsnede belast door buigmomenten en normaalkrachten in de richting van de controle. Waarden van hefboomarmen voor interne krachten voor alle combinatietypes worden weergegeven in de tabel Herberekende krachten in de navigator Interne krachten in doorsnede. |
Berekening van interne krachten aan beide oppervlakken
De hoofdkrachten aan beide oppervlakken van het 2D-element worden berekend met de formule:
\[{{n}_{1,bot\left( top \right)}}=\frac{{{n}_{x,low\left( upp \right)+}}{{n}_{y,low\left( upp \right)}}}{2}+\frac{1}{2}\sqrt{{{\left( {{n}_{x,low\left( upp \right)-}}{{n}_{y,low\left( upp \right)}} \right)}^{2}}+4\cdot {{n}_{xy,low\left( upp \right)}}}\]
\[{{n}_{2,bot\left( top \right)}}=\frac{{{n}_{x,low\left( upp \right)+}}{{n}_{y,low\left( upp \right)}}}{2}-\frac{1}{2}\sqrt{{{\left( {{n}_{x,low\left( upp \right)-}}{{n}_{y,low\left( upp \right)}} \right)}^{2}}+4\cdot {{n}_{xy,low\left( upp \right)}}}\]
En de richting van de hoofdkrachten wordt berekend met de formule:
\[{{\alpha }_{n1,low\left( upp \right)}}=0,5\cdot {{\tan }^{-1}}\left( \frac{2\cdot {{n}_{xy,low\left( upp \right)}}}{{{n}_{x,low\left( upp \right)}}-{{n}_{y,low\left( upp \right)}}} \right)\]
| Opmerking: |
| De hoofdkrachten en de richting van de hoofdkrachten voor beide vlakken van het 2D-element worden voor alle combinatietypes weergegeven in de tabel Herberekende krachten in de navigator Interne krachten in sectie. |
Berekening van herberekende interne krachten op vlakken naar de gedefinieerde controlerichting
De herberekening van de hoofdkrachten naar de controlerichtingen wordt voor elk oppervlak afzonderlijk uitgevoerd met behulp van de Baumann-transformatieformule:
\[{{n}_{surface,i,low\left( upp \right)}}=\frac{{{n}_{1,low\left( upp \right)}}\cdot \sin \left( {{\alpha }_{j,low\left( upp \right)}} \right)\cdot \sin \left( {{\alpha }_{k,low\left( upp \right)}} \right)+{{n}_{2,low\left( upp \right)}}\cdot \cos \left( {{\alpha }_{j,low\left( upp \right)}} \right)\cdot \cos \left( {{\alpha }_{k,low\left( upp \right)}} \right)}{\sin \left( {{\alpha }_{j,low\left( upp \right)}}-{{\alpha }_{i,low\left( upp \right)}} \right)\cdot \sin \left( {{\alpha }_{k,low\left( upp \right)}}-{{\alpha }_{i,low\left( upp \right)}} \right)}\]
| Beschrijving | |
| i, j, k, i | Index van de controlerichting (herberekeningsrichting van interne krachten) i, j, k, i = 1, 2, 3, 1 . Bijv. voor ondervlak en berekening van kracht in j-richting (hoek α2) is de formule: \[{{n}_{surface,2,low}}=\frac{{{n}_{1,low}}\cdot \sin {{\alpha }_{3,low}}\cdot \sin {{\alpha }_{1,low}}+{{n}_{2,low}}\cdot \cos {{\alpha }_{3,low}}\cdot \cos {{\alpha }_{1,low}}}{\sin \left( {{\alpha }_{3,low}}-{{\alpha }_{2,low}} \right)\cdot \sin \left( {{\alpha }_{1,low}}-{{\alpha }_{2,low}} \right)}\] |
| \[{{\alpha }_{i,j,k,low\left( upp \right)}}\] | De hoek tussen de gedefinieerde controlerichting of de richting van de drukstut en de richting van de hoofdkrachten aan de onder- of bovenkant van het 2D-element. Bepaalde controlerichting α1, low(upp) = α1 – α low(upp) Dir. loodrecht op de gedefinieerde richting α2, low(upp) = α2 – α low(upp) Contourrichting voor drukstut α3, low(upp) = α3 – α low(upp) |
| α1 | Bepaalde controlerichting voor de specifieke combinatie |
| α2 | De richting loodrecht op de gedefinieerde richting, α2 = α1 + 90 graden |
| α3 | Controleer de richting in de richting van de drukstut in het vlak van het 2D-element. Deze richting is geoptimaliseerd om de kracht in deze richting te minimaliseren. |
| Opmerking: |
Als de controlerichting identiek is aan de richting van de hoofdspanningen, zijn de krachten in de drukstaaf nul, dus wordt deze richting verwaarloosd in de controle. De richting van de drukstut voor alle spanningstoestanden behalve de hyperbolische spanningstoestand (n1,low(upp) > 0 and n1,low(upp) < 0) kan berekend worden met de formule: α3 = 0,5(α1 + α2) Herberekende interne krachten voor beide oppervlakken van het 2D element en alle controle richtingen inclusief de richting van de drukstaaf worden weergegeven in de tabel Herberekende krachten |
Transformatie van herberekende interne krachten naar het zwaartepunt van de doorsnede
Voor de controle van het 2D-element moeten de oppervlaktekrachten in een bepaalde richting herberekend worden naar het middelpunt van de doorsnede. Het resultaat is de normaalkracht nd,i en het buigmoment md,I die werken in het middelpunt van de doorsnede van het 2D-element.
md,i = nlower,i·zs,low + nupper,i·zs,upp
nd,i = nlower,i + nupper,i
| Beschrijving | |
| nlower,i | Herberekende oppervlaktekrachten op het onderste oppervlak in de i-de controlerichting, wanneer nlower,i = nsurface,low,i. |
| nupper,i | Herberekende interne krachten op het bovenste oppervlak in de i-de controlerichting, wanneer nupper,i = nsurface,upp,i. |
| zs,low (upp) | Afstand van het middelpunt van beton onder druk of het middelpunt van wapening aan het onderste (bovenste) oppervlak, wanneer z = zs,low + zs,upp |
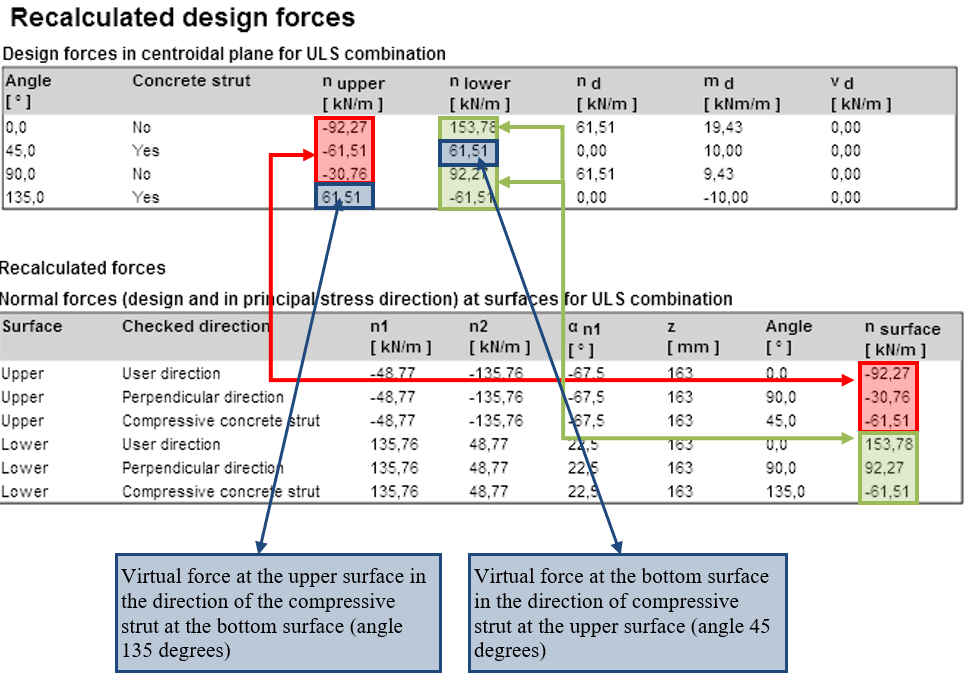
| Opmerking: |
| Als de richtingen van de drukstaven aan het onderste en bovenste oppervlak verschillend zijn, is het voor de herberekening van de krachten naar het middelpunt nodig om de virtuele krachten aan het onderste oppervlak te berekenen in de richting van de drukstaven aan het bovenste oppervlak en omgekeerd. |
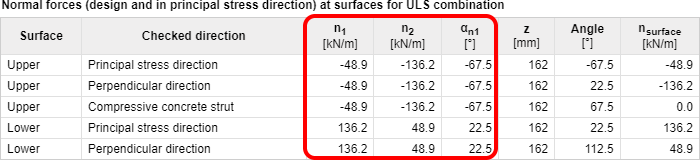
Herberekende interne krachten.
Herberekening van dwarskrachten naar de gedefinieerde richting
De dwarskrachten worden herberekend naar de richting van de controle met behulp van de formule:
\[{{v}_{d,i}}={{v}_{x}}\cdot \cos ({{\alpha }_{i}})+{{v}_{y}}\cdot \sin ({{\alpha }_{i}})\]
en de maximale dwarskracht is:
\[{{v}_{d,max~}}=\sqrt{{{v}_{x}}^{2}+{{v}_{y}}^{2}}\]
en werkt in de richting
\[\beta ={{\tan }^{-1}}\left( \frac{{{v}_{y}}}{{{v}_{x}}} \right)\]
| Beschrijving | |
| αi | Controleer de hoek in de i-de richting |
| Opmerking: |
| Bij het controleren van een 2D element met relatief grote dwarskrachten is het geschikt om het 2D element te controleren in de richting van de maximale dwarskracht, wat betekent dat de gedefinieerde richtingcontrole overeenkomt met hoek β |
Vergelijking van herberekening van interne krachten met verschillende methoden
Herberekening van krachten volgens EN 1992-1-1
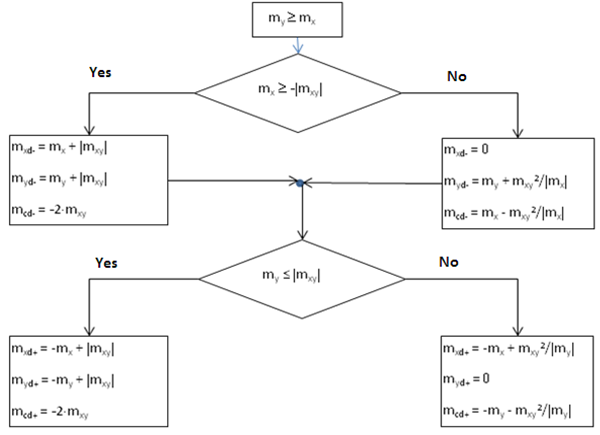
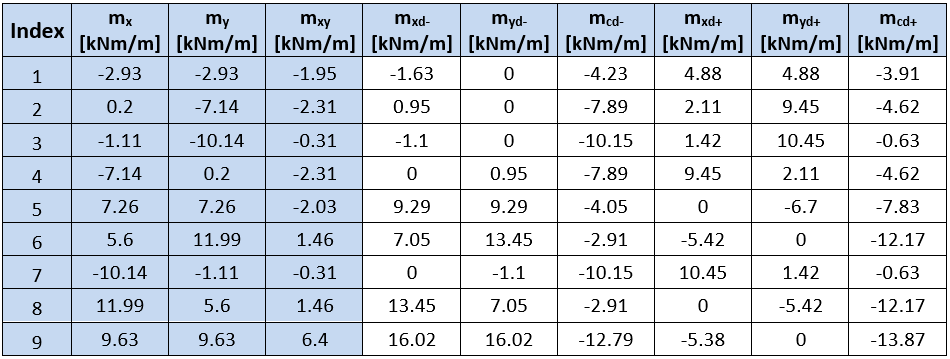
De methode beschreven in EN 1992-1-1 wordt in verschillende programma's en in de praktijk gebruikt om ontwerp-krachten te berekenen. EN 1992-1-1 houdt alleen rekening met loodrechte wapeningsrichtingen. De berekening van dimensioneringskrachten met de invloed van torsiemomenten wordt beschreven in het volgende stroomschema, waarbij my³ mx. Een soortgelijk diagram kan worden gemaakt voor momente my < mx
| Beschrijving | |
| mxd+, mxd- | Dimensionering van het buigmoment in de x-asrichting voor ontwerp en controle van wapening aan het onderste (-) of bovenste (+) oppervlak |
myd+ myd- | Dimensionering van het buigmoment in de y-richting voor ontwerp en controle van wapening aan het onderste (-) of bovenste (+) oppervlak |
| mcd+, mcd- | Dimensionering van het buigmoment in de drukbetondiagonaal aan het onderste (-) of bovenste (+) oppervlak, dat door beton moet worden gedragen |
Waarden van herberekende dimensioneringskrachten voor het type element = plaat, berekend volgens de methode beschreven in EN, worden weergegeven in de volgende tabel:
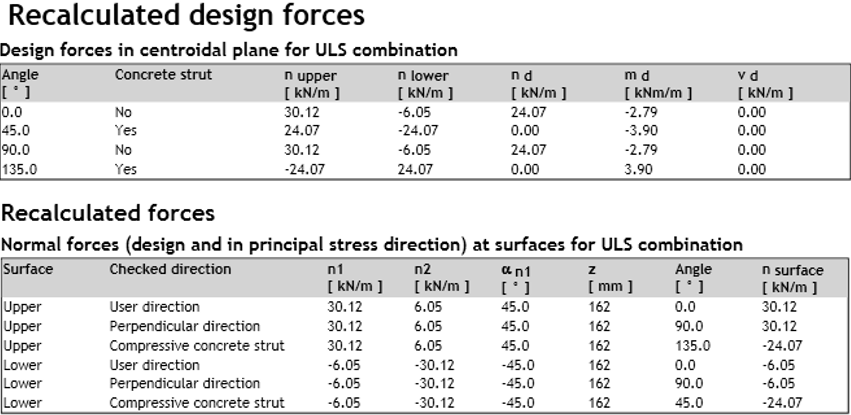
In IDEA StatiCa RCS worden de waarden van momenten op het boven- en ondervlak niet weergegeven, maar de waarden van normaalkrachten op beide vlakken en de waarden van momenten herberekend naar het middelpunt van de doorsnede.
Momenten aan het onderste en bovenste oppervlak kunnen worden berekend met behulp van oppervlaktekrachten, die worden weergegeven in de numerieke uitvoer, met behulp van de formule:
\[{{m}_{surface,i,dlow\left( upp \right)}}={{n}_{surface,i,low\left( upp \right)}}\cdot z\]
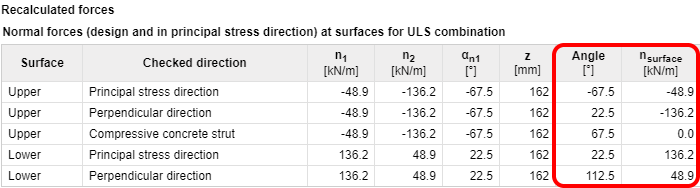
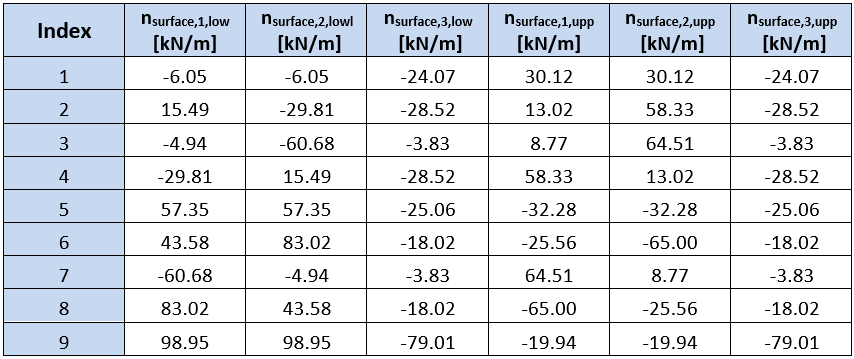
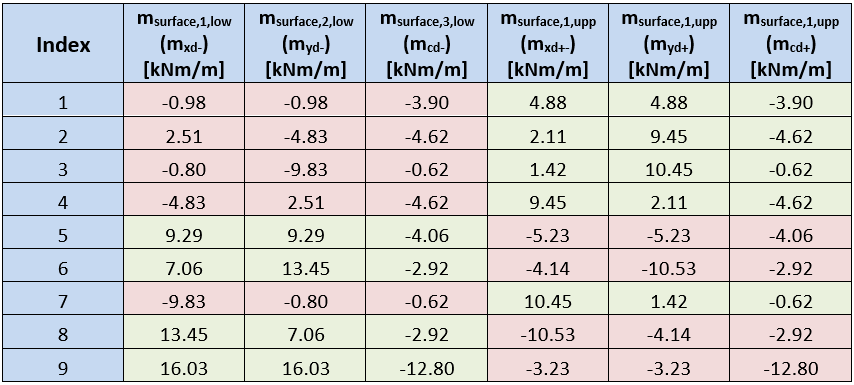
De waarden van de oppervlaktekrachten en herberekende momenten worden weergegeven in de volgende tabellen:
De tabellen laten zien dat momenten op plaatoppervlakken berekend in IDEA Concrete en berekend volgens de methode beschreven in EN, slechts op één oppervlak overeenkomen. Dit verschil wordt veroorzaakt door een verschillende optimalisatie van de betonnen drukstaaf. De methode gebruikt in IDEA StatiCa RCS zoekt naar de hoek van de drukdiagonaal bij de minimale kracht in de staaf. De methode beschreven in EN zoekt naar een minimale som van negatieve krachten uit alle richtingen.
Vergelijking van berekening van interne krachten met de programma's RFEM en SCIA Engineer
Om de resultaten van de herberekende interne krachten in de programma's IDEA Concrete, RFEM en SCIA Engineer te vergelijken, werd een eenvoudig model van een plaat met afmetingen 6 m x 4 m en een dikte van 200 mm voorbereid. De plaat wordt ondersteund met lijnsteunen aan de randen en belast met een uniforme belasting van 10 kN/m2.
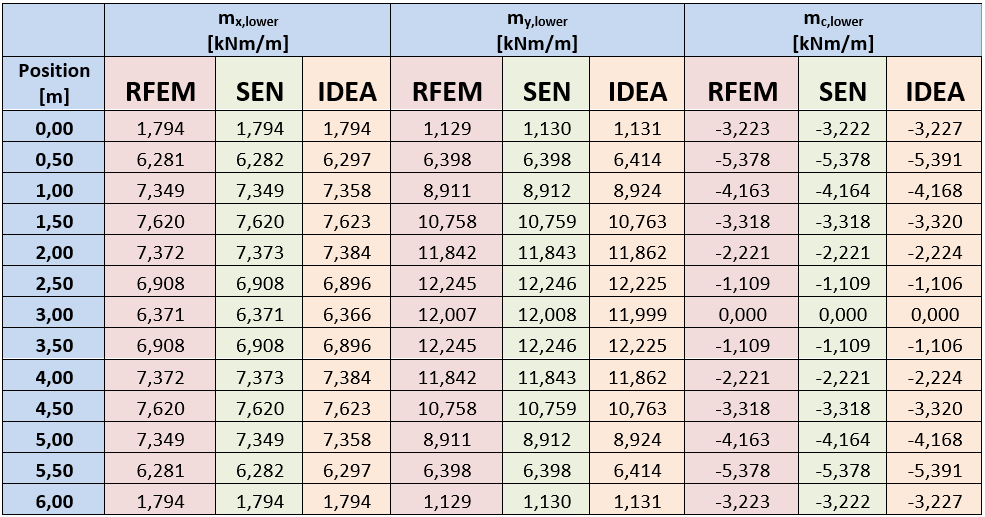
Om de presentatie te vereenvoudigen worden alleen de waarden van de herberekende interne krachten in één langsdoorsnede weergegeven. De sectieafstand vanaf de rand van de plaat is 1,5 m. De interne krachten berekend in het programma RFEM werden gebruikt als invoerwaarden voor IDEA Concrete.
De tabel toont een goede overeenstemming van de krachten berekend in bepaalde programma's.