Compression softening effect - 2D planar pile caps
Introduction:
This experimental investigation presents results and a discussion on a series of two reinforced concrete pile caps with and without inclined rebar, measuring 400× 400 × 1000 mm, which were tested under concentric loading. The study set was created from concrete with a compressive strength of 25.8 MPa and reinforcement rebars with diameters of 5, 10, and 12.5 mm. The verification was conducted in FEA solution - ABAQUS leveraged 3D volume elements and IDEA StatiCa 2D Detail build-up on the CSFM(Compatible Stress Field Method) with preassumption of 2D plane stress. The main tensile bars and concrete struts in the pile cap have been dimensioned based on the experimental works previously developed by Blévot and Frémy [4]. The goal of the verification was to conduct a series of numerical simulations to compare the bearing capacity of the solutions with real - tests and pilot the conclusions on the impact of compression softening for discontinuity regions as planar pile caps where the shear failure was primary damage and can lead to fatal disaster if underestimated.
Experimental setup
The experiment was instructed by the team consisting of Aaron Nzambi, Lana Gomes, Cledinei Amanajás, Francisco Silva, and Dênilo Oliveira [1] with the ambition of studying the effects of steel fibers and inclined shear reinforcements on the bearing capacity of the pile cap.
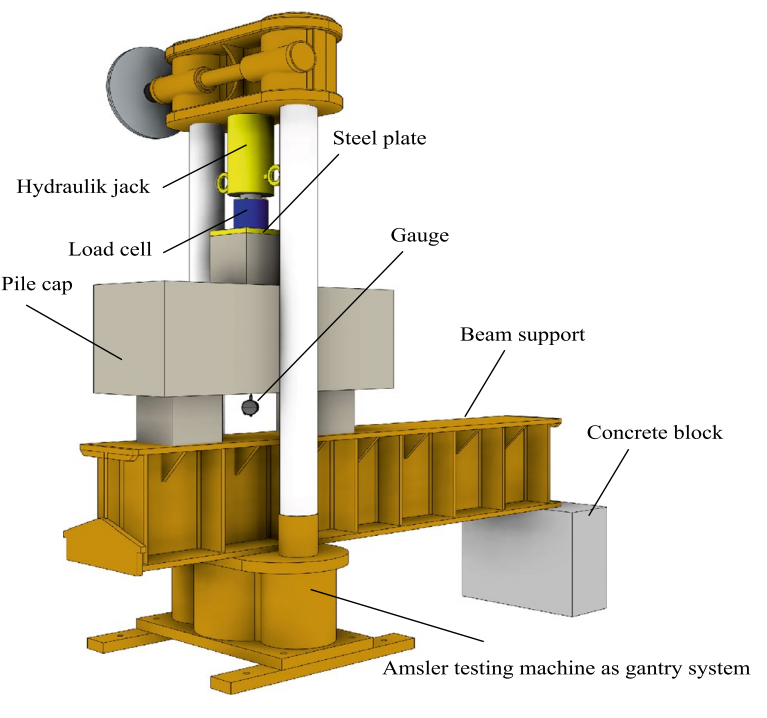
All samples were subjected to centered loading applied on the face of the column using a hydraulic jacket over the steel plate for uniform distribution. The steel beam with rigid stiffeners was used as support during the loading. The gauge was fastened on the bottom surface of the pile-cap body directly between two piles, where the final deformation was measured and evaluated. More gauges have been utilized on reinforcement surfaces—more information can be searched in the article [1]. The loading has been quasi-static and short-term to avoid the effect of rate-dependent behavior-rheology effects.
\[ \textsf{\textit{\footnotesize{Fig. 1\qquad Test assembly and gauges - installed strain gauges(left), deflectometer position (right)}}}\]
Geometry and reinforcements
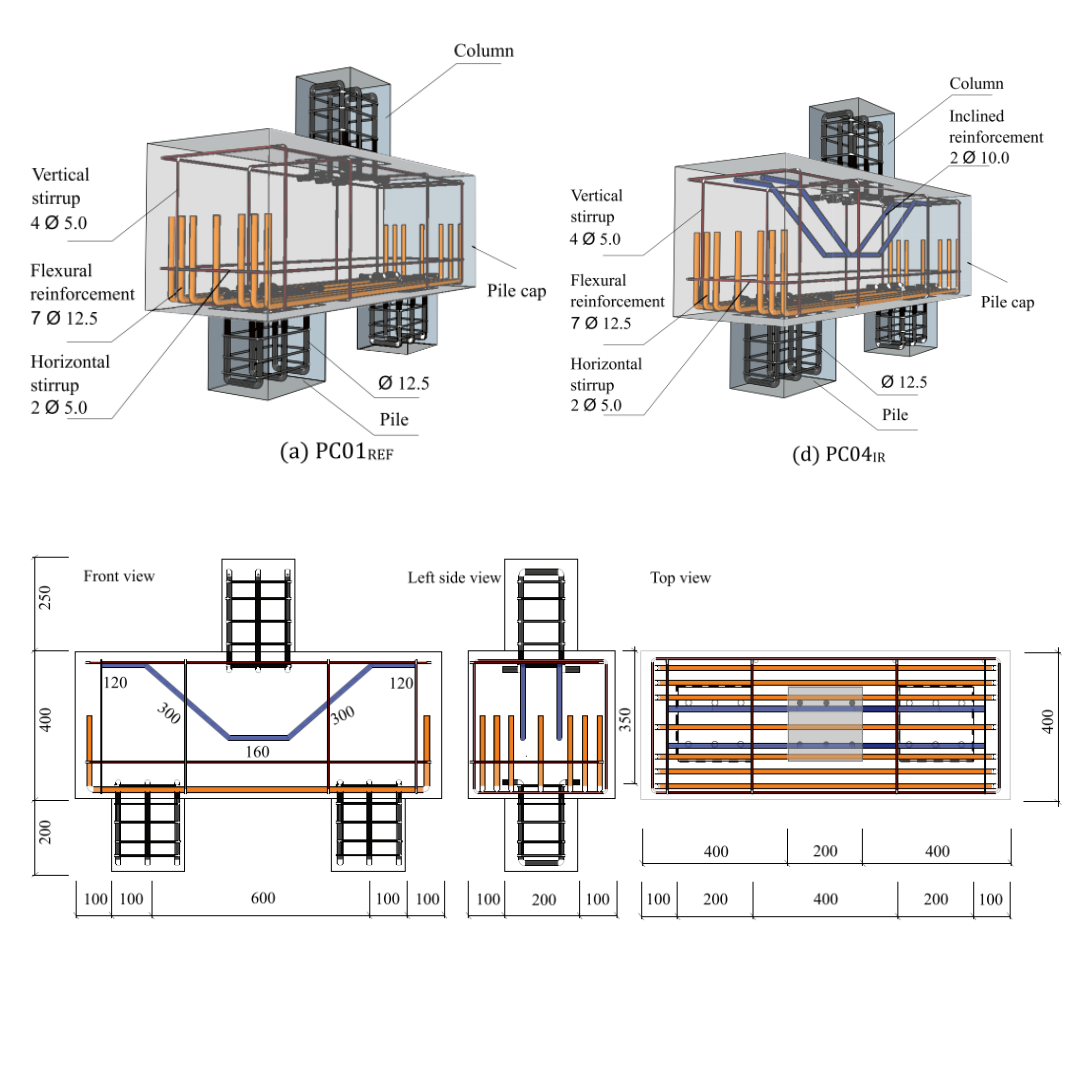
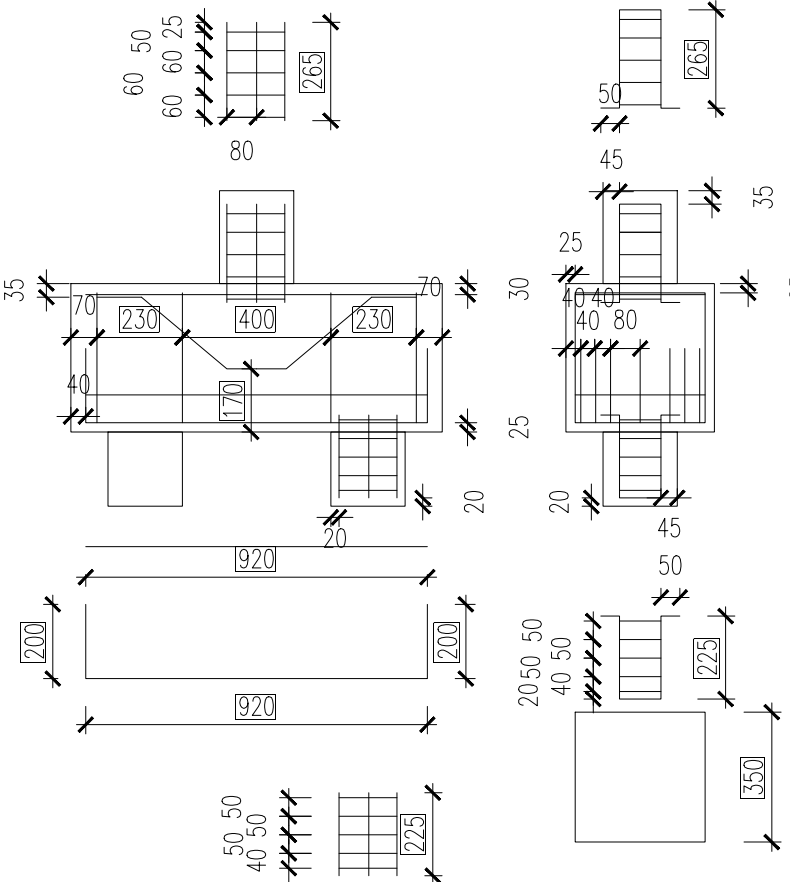
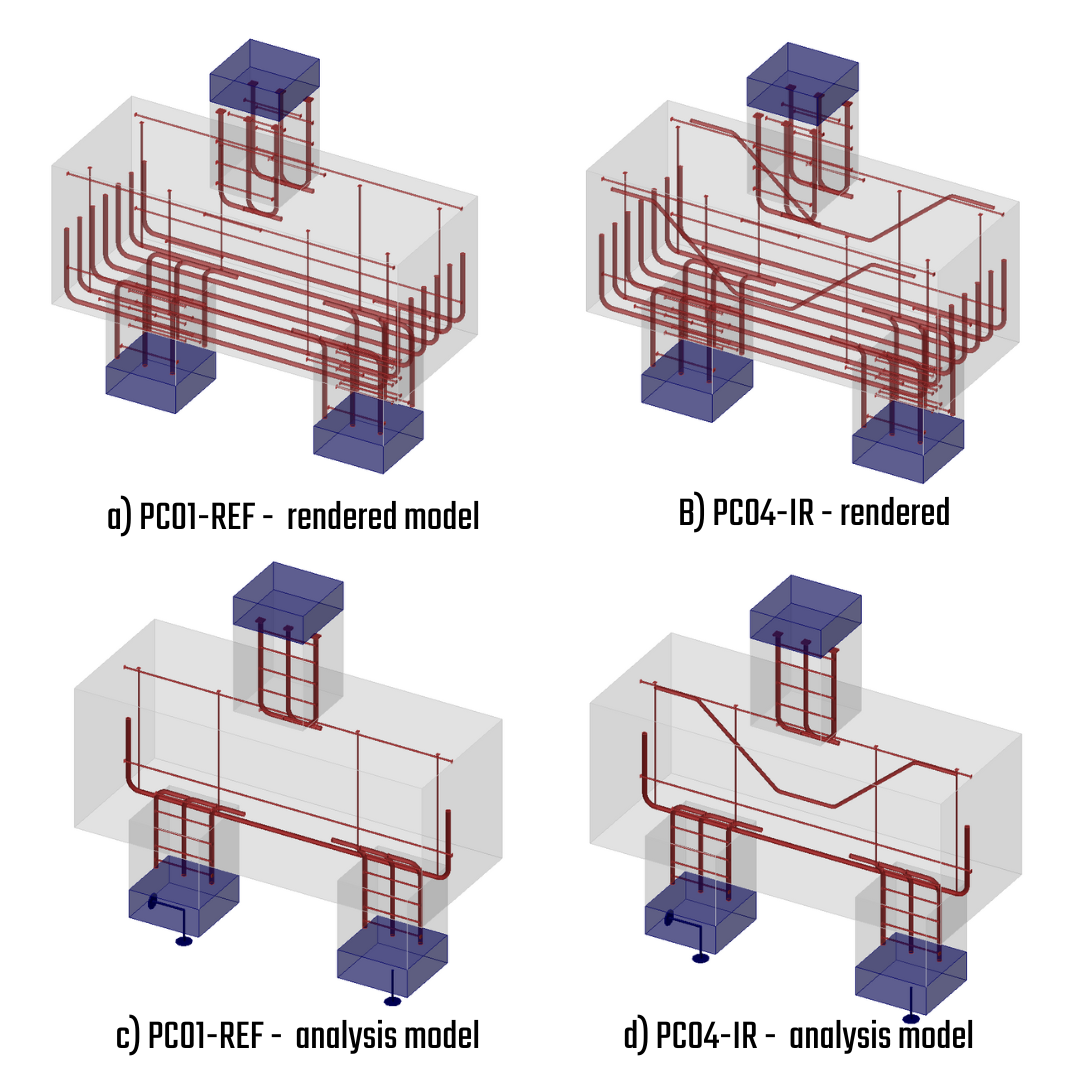
If we maintain the labeling of the specimens as indicated in the article [1], the tested samples, PC01REF and PC04IR, have been submitted for verification purposes. The dimensions of the specimens are identical; however, the differences in contrast are due to the arrangement of the reinforcements. In the case of specimen PC04IR, an inclined bar is included to capture transverse tensile strains in the concrete and to strengthen this area.
\[ \textsf{\textit{\footnotesize{Fig. 2\qquad Reinforcement setup and dimensions}}}\]
Material and physical properties
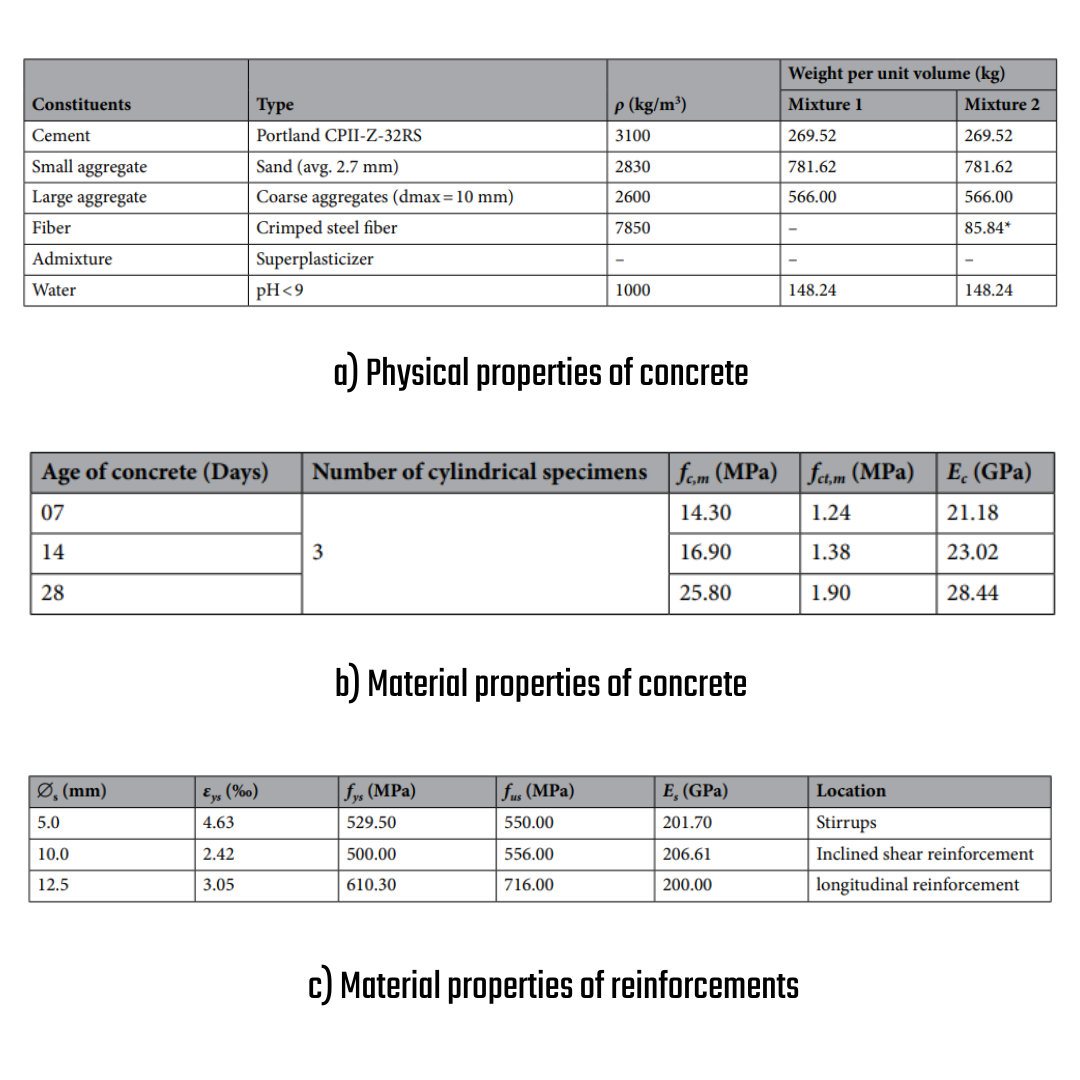
Cement, coarse aggregate, fine aggregate, and water–cement ratio (w/c) were mixed in a 1:2.90:2.10:0.55 proportion. Superplasticizer additive was used to maintain the constant workability of concrete. The concrete test specimens were molded and cured for 28 days in the laboratory with 85% relative air humidity. The tab. presents the results of the characterization tests at 7, 14, and 28 days. The average values were adopted: 25.8 MPa, 1.9 MPa, and 28.4 GPa, respectively, for compressive strength (fc), tensile strength (fct), and modulus of elasticity (Ec). The steel bars used in the tests were classifed according to NBR 748015. Their mechanical properties were determined through axial tensile tests, following the recommendations of NBR ISO 6892-116 [6]. Tree samples were used in the tensile test; the test bars measured 5.0 mm, 10.0 mm, and 12.5 mm in diameter and were used in the stirrups, inclined shear reinforcement, and flexural reinforcement, respectively.
\[ \textsf{\textit{\footnotesize{Fig. 3\qquad Material and physical properties}}}\]
IDEA StatiCa 2D Detail - CSFM
The Compatible Stress Field Method (CSFM) is a continuous FE-based stress field analysis method in which classic stress field solutions are complemented with kinematic considerations, i.e., the state of strain is evaluated throughout the structure. Hence, the effective compressive strength of concrete can be automatically computed based on the state of transverse strain in a similar manner as in compression field analyses that account for compression softening (Vecchio and Collins 1986; Kaufmann and Marti 1998) and the EPSF method (Fernández Ruiz and Muttoni 2007). Moreover, the CSFM considers tension stiffening, providing realistic stiffnesses to the elements, and covers all design code prescriptions (including serviceability and deformation capacity aspects) not consistently addressed by previous approaches. Concrete in tension is entirely neglected and the CSFM uses common uniaxial constitutive laws provided by design standards for concrete and reinforcement. These are known at the design stage, which allows the partial safety factor method to be used. Hence, designers do not have to provide additional, often arbitrary material properties as are typically required for non-linear FE-analyses, making the method perfectly suitable for engineering practice.
More information about the method is outlined in the theoretical background.
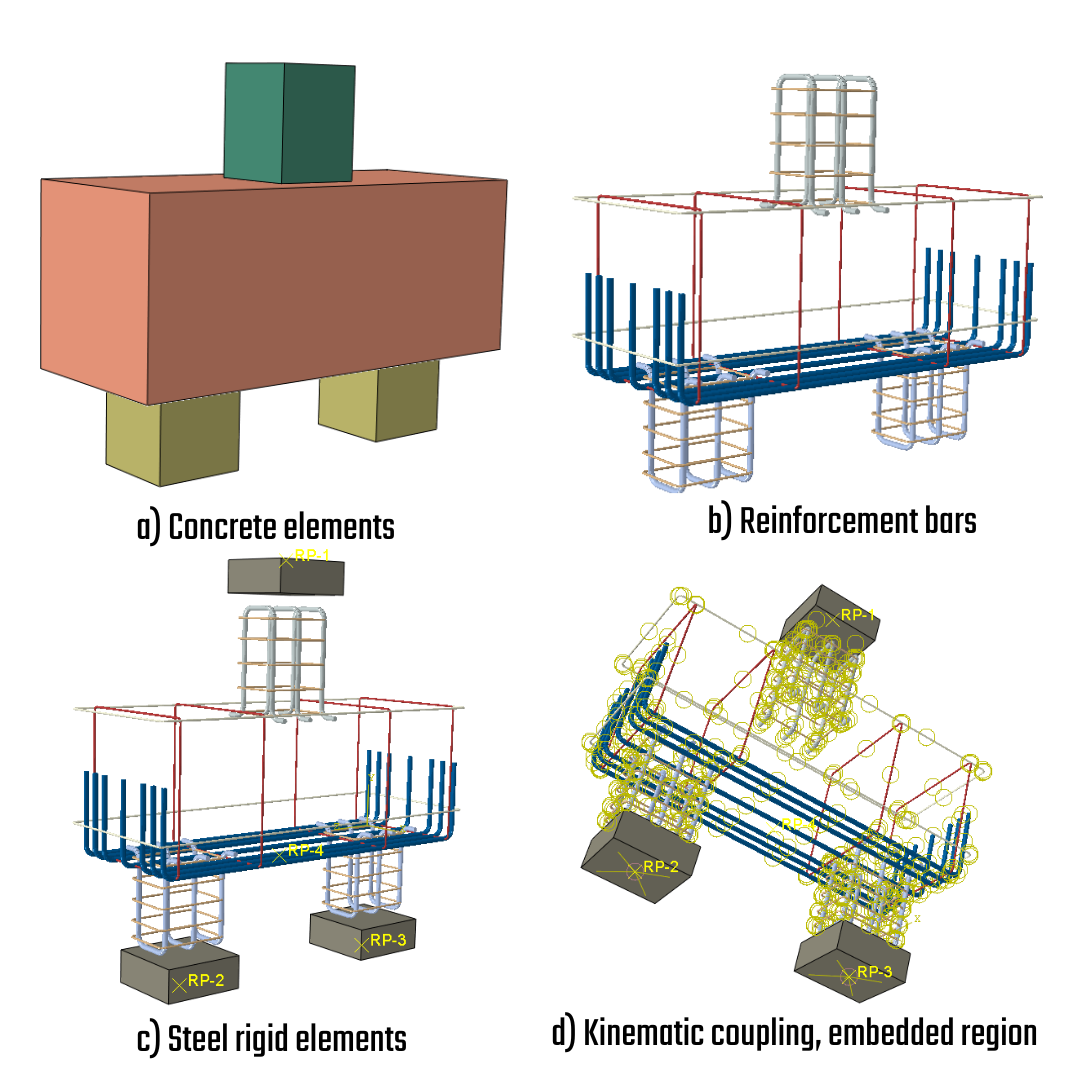
Model assembly
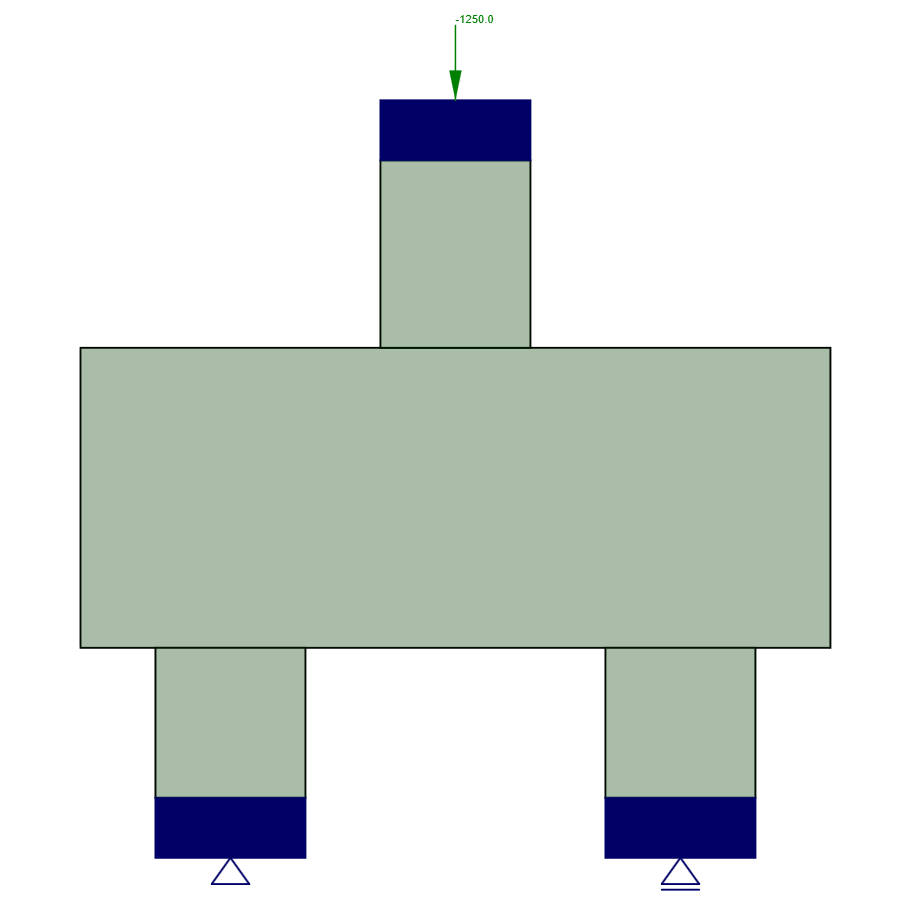
The model consists of four concrete blocks that represent the body of the pile cap, the piles, and the column. The dimensions and thicknesses were determined based on the experimental setup. This model is simply supported; the left support restricts both horizontal and vertical translations, while the right support restricts only vertical translations. Point supports with steel bearing plates are used to ensure stability. These bearing plates are artificially thick - 80 mm to ensure an even distribution of stresses. As the structure behaves like a simply supported beam, the height of the bearing plates does not significantly affect the results.
A custom steel material with an intentionally high modulus of elasticity was utilized to model the bearing plates. Due to the geometry of the structure and the loading conditions, the highest compression stresses occur around the bottom edges of the column where the column is cast to the pile body. Although these compression stresses exceed the concrete's compressive strength, the structure did not lose the integrity and strength due to the confinement effect. Since the 2D model cannot capture the effects of stress triaxiality, a custom material with increased compressive strength was used to model the pile and column elements. All material safety factors are set equal to 1.0 due to experimental setup comparison.
\[ \textsf{\textit{\footnotesize{Fig. 4\qquad Reinforcements rendering, analysis model}}}\]
Loads
A concentrated force is applied through a plate with an increased modulus of elasticity to ensure a uniform distribution of stress across the top surface of the column. In the non-linear analysis (NR-analysis), the maximum force is reached once the stopping criteria are satisfied. As a result, the model may become overloaded, causing the analysis to stop before the applied load reaches 100%. This approach is optimal for achieving the critical force.
\[ \textsf{\textit{\footnotesize{Fig. 5\qquad Concentrated force on the top plate}}}\]
Compression softening
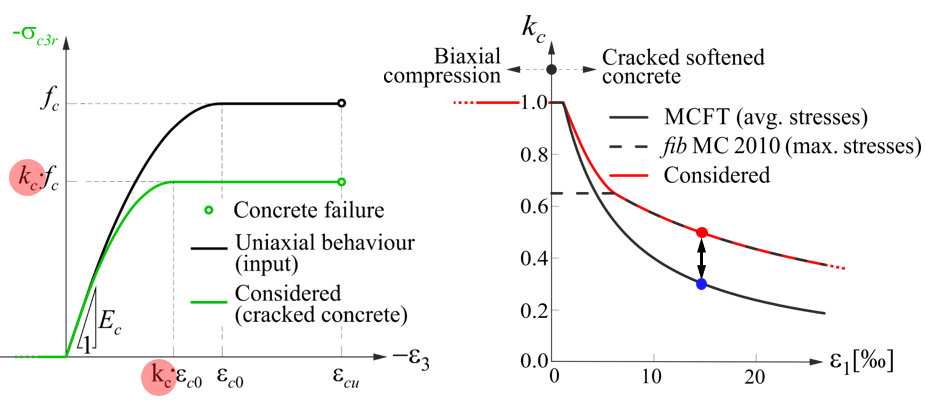
Compression softening in concrete structures refers to a reduction in the compressive strength and stiffness of concrete due to the presence of cracks or transverse tensile strains, especially in reinforced concrete elements subjected to combined stresses.
What is Compression Softening?
Compression softening is a mechanical degradation phenomenon where:
- Concrete under compression exhibits reduced capacity when it is simultaneously cracked in tension or undergoing shear deformations.
- This is especially observed in cracked concrete subjected to compression, like in shear walls, struts, or web elements of beams.
Why Does It Happen?
Concrete is a brittle material. When cracks form (due to tension, bending, or shear), the stress distribution inside the material changes:
- Cracks allow lateral expansion (transverse strain) of the concrete.
- When compressed, the cracked concrete can't resist loads as efficiently.
- This results in a reduction of its apparent compressive strength—hence, the term softening.
\[ \textsf{\textit{\footnotesize{Fig. 6\qquad Compression softening representation in 2D Detail}}}\]
Mesh sensitivity
Evaluates how the results of a numerical simulation change with varying mesh sizes. It helps determine the optimal mesh that balances accuracy and computational cost. A finer mesh generally yields more accurate results but at higher computational expense. The goal is to ensure results are independent of mesh size, indicating numerical stability and reliability of the model.
Based on the statement above, we conducted simulations with different mesh sizes to determine the optimum for accuracy. Two sets of sensitivity analyses for compression softening, on and off, were performed for the models PC01REF and PC04IR. The compression softening effect is hardcoded and by default considered.
The experiment threshold reveals the maximum load our testing specimens can handle! Excitingly, all models concluded with shear failure in the pile cap body, showcasing valuable insights!
PC01REF compression softening - on
When compression softening is activated, the discrepancy between the experimental threshold and the different mesh multipliers ranges from 0% to 18%. The best-fitting results are achieved with a mesh multiplier of 0.5, where we obtain a bearing capacity that matches the experimental results. In contrast, using the default mesh multiplier of 1 slightly overestimates the bearing capacity of the numerical model.
\[ \textsf{\textit{\footnotesize{Fig. 7\qquad Mesh sensitivity compression softening on}}}\]
PC01REF compression softening - off
When compression softening is deactivated, the difference between the experimental threshold and the various mesh multipliers ranges from 16% to 42%. This discrepancy indicates a significant error, which remains on the dangerous side. These findings are crucial for the design of planar pile caps.
It was also observed that models with activated compression softening exhibit improved ductility in the hardening region. Conversely, the experiments revealed a brittle failure due to the lack of inclined bars, which is a significant concern that should be addressed during the design process.
\[ \textsf{\textit{\footnotesize{Fig. 8\qquad Mesh sensitivity compression softening off}}}\]
PC04IR compression softening - on
When compression softening is activated, the difference between the experimental threshold and the various mesh multipliers ranges from 10% to 18%. Since all the curves fall below the experimental threshold, this indicates a safe margin. These results pertain to a model that features an inclined shear bar. This safety margin is in contrast to model PC01REF. The inclined bars in the area of compression softening enhance the model's strength and result in a higher safety margin for simulations using CSFM.
\[ \textsf{\textit{\footnotesize{Fig. 9\qquad Mesh sensitivity compression softening on}}}\]
PC04IR compression softening - off
When compression softening is deactivated, the difference between the experimental threshold and the various mesh multipliers ranges from 6% to 11%. If the inclined shear reinforcements pass through the softened area, the bearing capacity for nearly all recommended mesh multipliers (0.5 and 1) in the final simulation falls below the experimental threshold. This leads to the conclusion that CSFM models without compression softening, when using inclined bars, remain safe, and collapse will not occur prematurely.
\[ \textsf{\textit{\footnotesize{Fig. 10\qquad Mesh sensitivity compression softening off}}}\]
ABAQUS - Concrete Damage Plasticity
Assumptions
Concrete Damage Plasticity (hereafter CDP) is based on the Drucker-Prager plasticity condition [7]. This model is suitable for materials with internal friction, such as soils or concrete. The tensile strength is significantly lower than the compressive strength and the hydrostatic part of the stress tensor plays a role in the evolution of the plasticity surface. Under general stress, the plasticity condition has the surface of a rotating cone. The material model for compressive and tensile stresses also considers post-critical behavior, which is controlled by the so-called damage parameters, taking values from zero (undamaged) to one (for near-zero stiffness of concrete in compression or tension in the post-critical condition). The larger the damage parameter number, the more the element is violated and does not contribute to the stiffness contribution.
The model is a continuum, plasticity-based damage model for concrete, accounting for tensile cracking and compressive crushing. It uses two hardening variables—tensile and compressive equivalent plastic strains—to control the failure surface. Concrete exhibits elastic behavior up to peak stress, followed by softening due to micro-cracking in tension and crushing in compression.
Material models
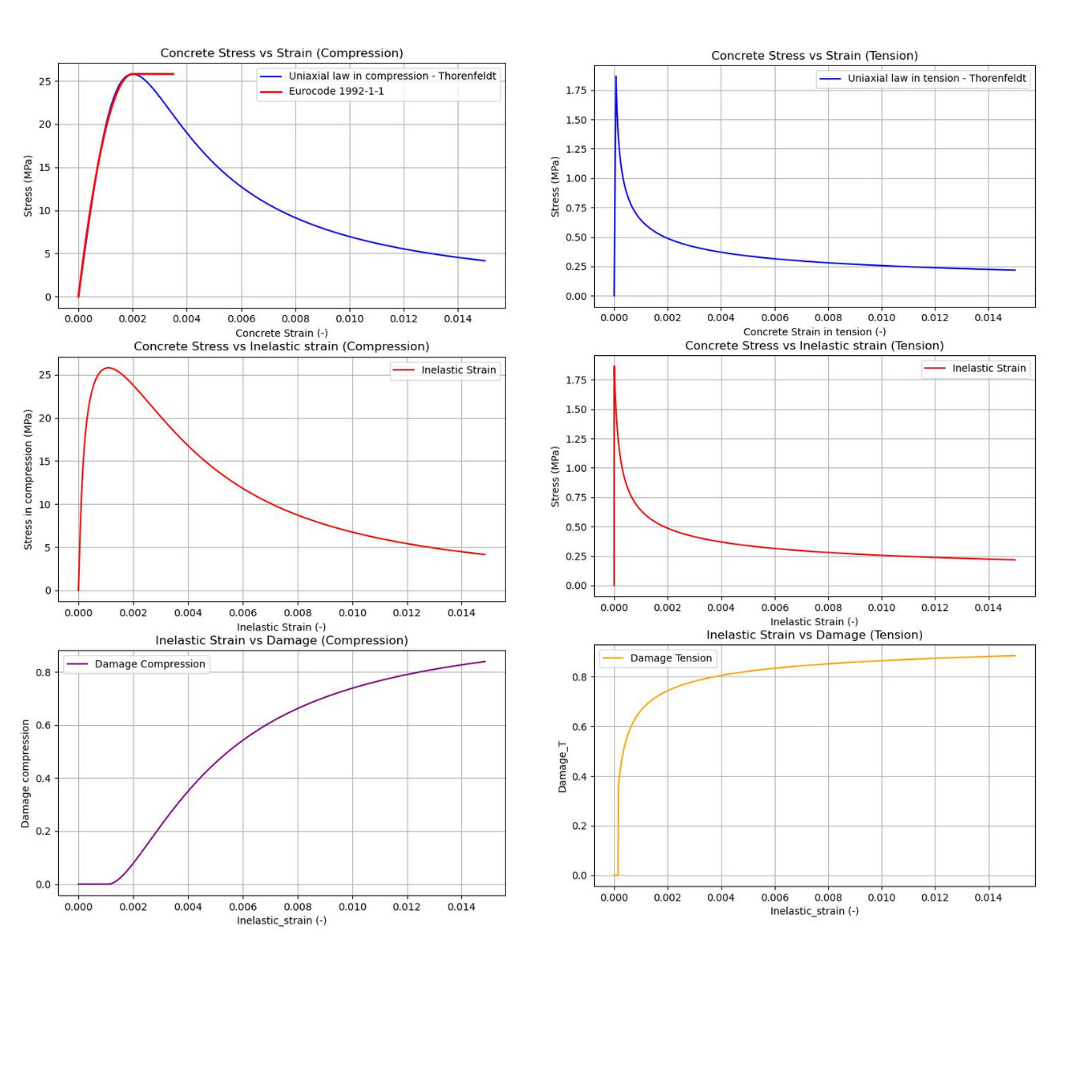
The Thorenfeldt model (more precisely, the Thorenfeldt–Tomaszewicz–Jensen model)[8] is a widely used empirical model for describing the nonlinear compressive stress-strain behavior of concrete, especially in concrete damage models in finite element analysis (FEA). This model is selected as a constitutive model for concrete damage plasticity in our case. The uniaxial law in compression copies the trend of the parabolic-rectangular diagram for concrete according to EN 1992-1-1 [5] till the peak value. Post-critical behavior, as in compression as in tension, is Thorenfeldt's base.
\[ \textsf{\textit{\footnotesize{Fig. 11\qquad Concrete Damage Model in compression/tension + damage }}}\]
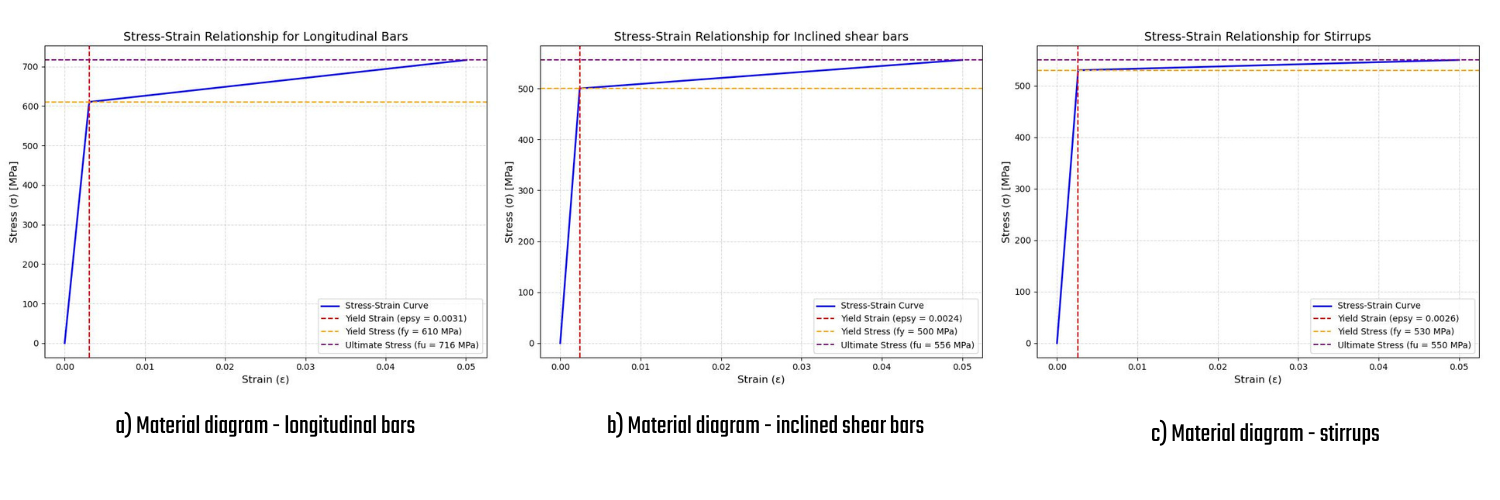
The bilinear material model with isotropic hardening for reinforcement bars has been selected. The material properties of each bar diameter are diverse.
\[ \textsf{\textit{\footnotesize{Fig. 12\qquad Bilinear diagram with hardening for reinforcement }}}\]
FEA elements
The C3D8, or hexa-element with a linear basis function and one integration points, was used for the FEM model of concrete. The reinforcement comprise T3D2 elements that transmit only axial effects. Ther interaction between reinforcement and concrete elements ensure constraints that are in-build inside the ABAQUS library and are called "Embedded feature".
The embedded element technique is used to specify that an element or group of elements is embedded in “host” elements. The embedded element technique can be used to model rebar reinforcement. ABAQUS searches for the geometric relationships between nodes of the embedded elements and the host elements. If a node of an embedded element lies within a host element, the translational degrees of freedom at the node are eliminated and the node becomes an “embedded node.” The translational degrees of freedom of the embedded node are constrained to the interpolated values of the corresponding degrees of freedom of the host element.
The kinematic coupling equations have been used for applying boundary conditions and load application. More elaboration downwards.
Model description
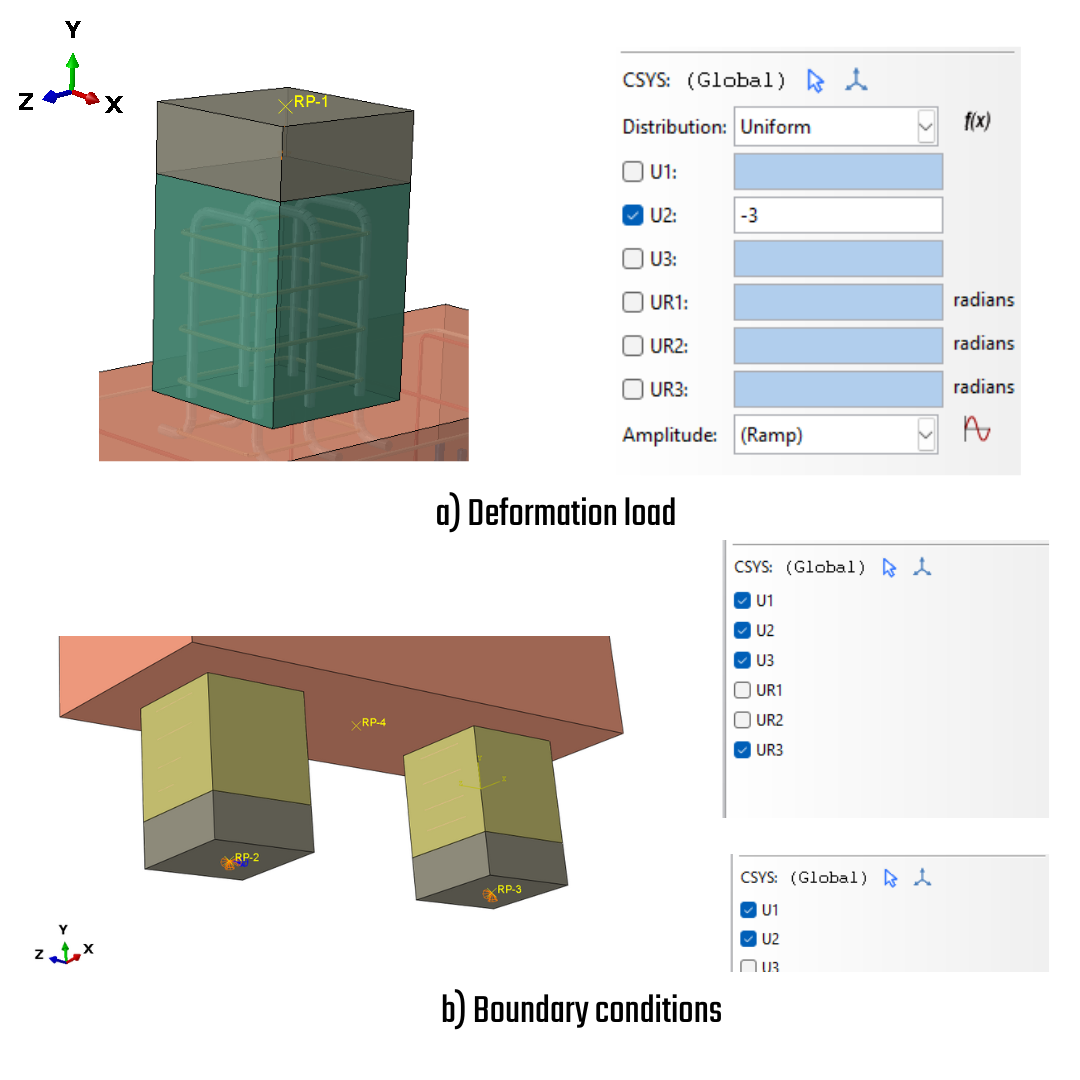
The column, body and piles are shielded by rigid steel plates to provide the equal stress distribution over the whole top surface column, where the load is applied and also in the bottom surfaces of piles where the boundary conditions are encountered. The load is transferred via the kinematic coupling constraint into the rigid element and the deformation load is placed onto the Reference point (RP1). Reference points RP2 and RP3 comprise the boundary conditions (BC).
\[ \textsf{\textit{\footnotesize{Fig. 13\qquad Model description ABAQUS }}}\]
Loads and boundary conditions
As has been mentioned above, the deformation load has been used to reach the post-critical stress state. The magnitude has been -3 mm in the Y-GCS. The BC for RP2 restrict all translation and one rotation degree of freedom. The RP3 restraints two translation degrees of freedom to create a simply hinged-supported system that will be stable in space.
\[ \textsf{\textit{\footnotesize{Fig. 14\qquad Loads and boundary conditions }}}\]
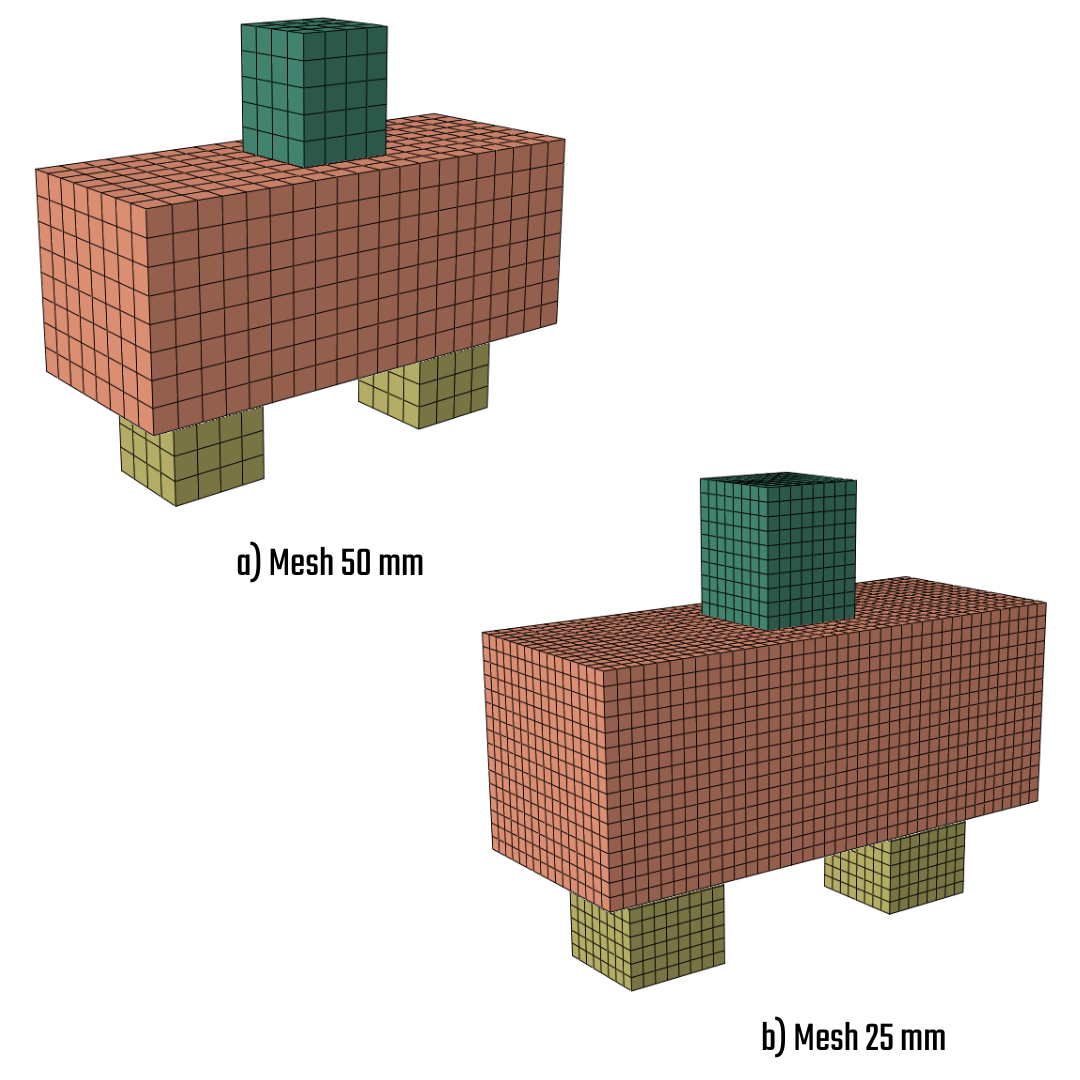
Mesh
Due to a mesh sensitivity study, two mesh sizes [25, 50] mm have been set up. The mesh has been applied to concrete and identically to reinforcement bars, with the exception of refinement in the area where the bend radius has been constructed.
\[ \textsf{\textit{\footnotesize{Fig. 15\qquad Mesh }}}\]
Mesh sensitivity ABAQUS
Mesh sensitivity evaluates how simulation results change with mesh refinement in finite element analysis. It ensures accuracy by identifying when further mesh refinement no longer significantly affects results, balancing precision with computational efficiency. The current outputs for mesh [50,25] mm prove that the rough mesh overestimates the experimental threshold by about 3 %, whereas the refined mesh 25 mm stays on the safe side and declares lower bearing capacity. The mesh 25 mm has been selected for further analysis and verification.
\[ \textsf{\textit{\footnotesize{Fig. 16\qquad Mesh sensitivity for the model PC01-REF }}}\]
Results
In this section, we will explore the outputs for analytical calculations, numerical solutions utilizing the CSFM ,CDP models, and experimental testing.
Experimental results
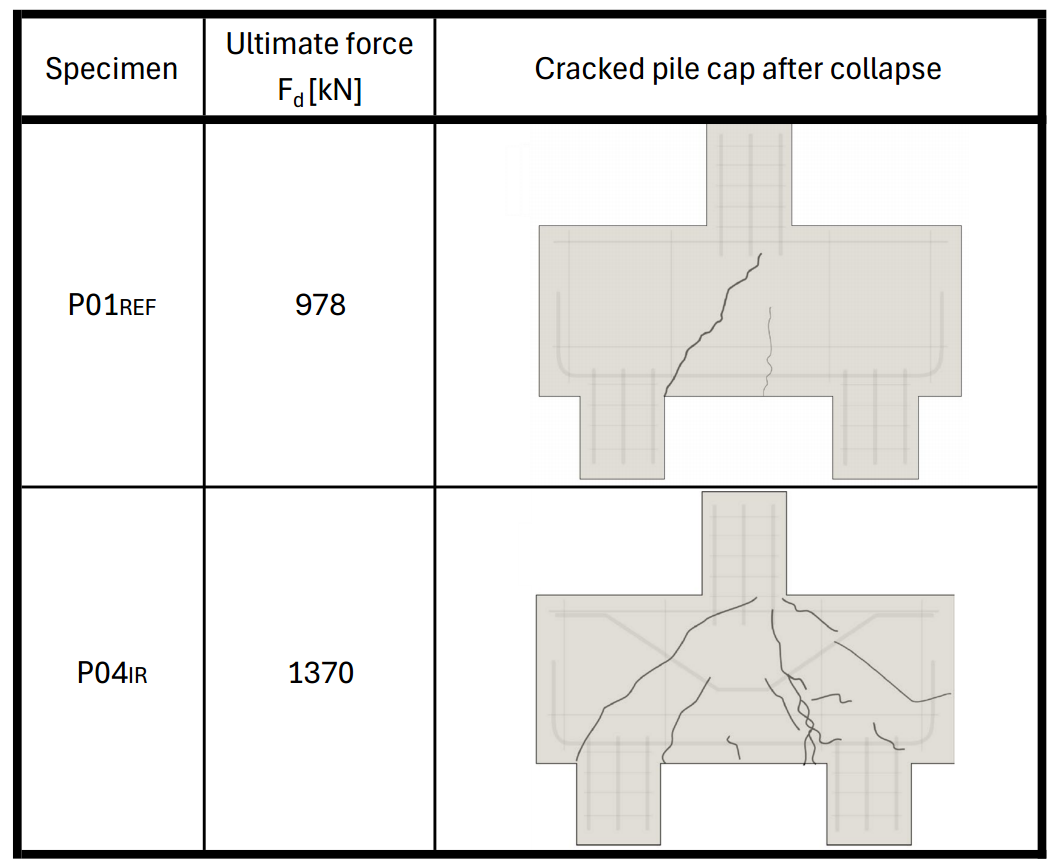
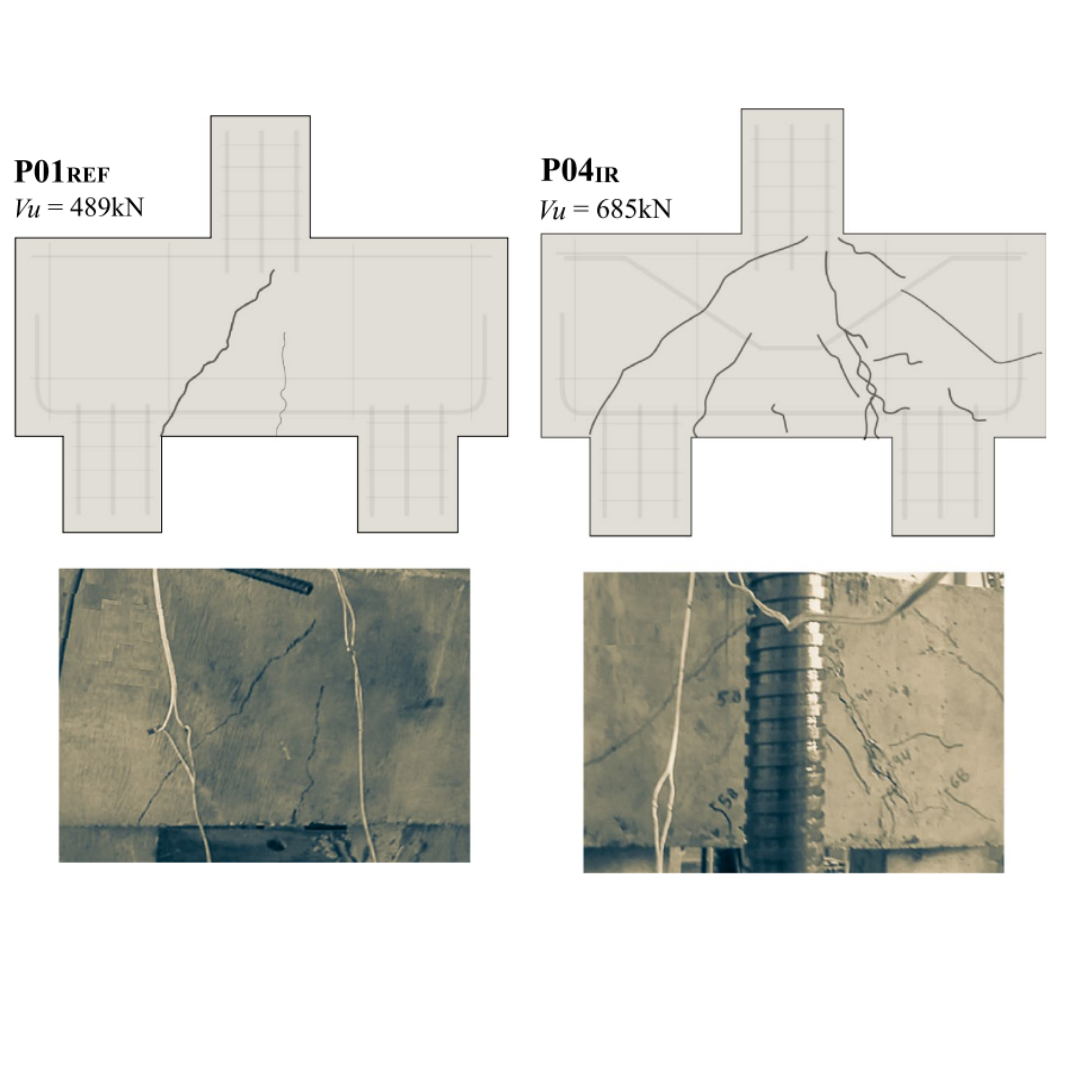
The experimental validation was conducted using the model PC01REF, which withstood a maximum transmitted force of 978 kN. The failure mode observed was shear, characterized by two dominant cracks that initiated on the bottom surface of the pile cap body. The first crack was identified as a bending crack with a subsequent effect of a shear crack triggering near the edge point of the pile.
In the second model, PC04IR, inclination bars were included, which enhanced the bearing capacity. In this model, the primary cracks exhibited a scattered pattern across the body of the pile cap. It leads to the fact that the model had a more appropriate reinforcement layout and a higher reinforcement ratio.
\[ \textsf{\textit{\footnotesize{Fig. 17\qquad Bearing capacity and crack propagation from the testing setup }}}\]
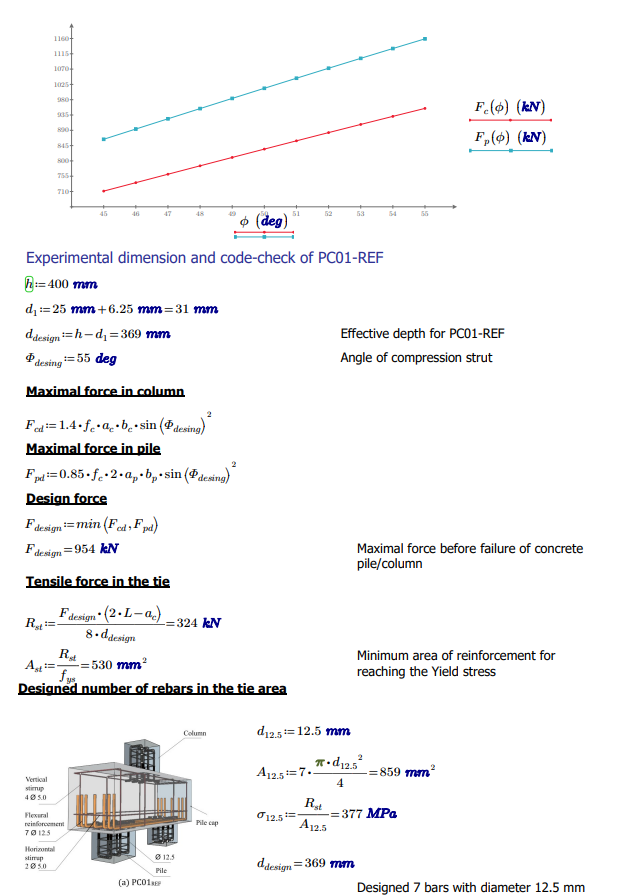
Strut and tie - analytical solution
In the current study, the pile caps were designed using the Strut-and-Tie method (STM), the most widespread calculation model for the design of rigid pile caps. This design is based on the experimental works previously developed by Blévot and Frémy[4]. The model consists of designing a spatial truss inside a pile cap using tension and compression bars that are connected through nodes, as shown in Figure 17. The calculation guarantees that the reinforcement bars in the tension (ties) will not reach the yield stress because of redundancy in the number of bars. The failure mode for S&T model will happen on the concrete based on the calculation and design of rebars.
\[ \textsf{\textit{\footnotesize{Fig. 18\qquad Strut and Tie }}}\]
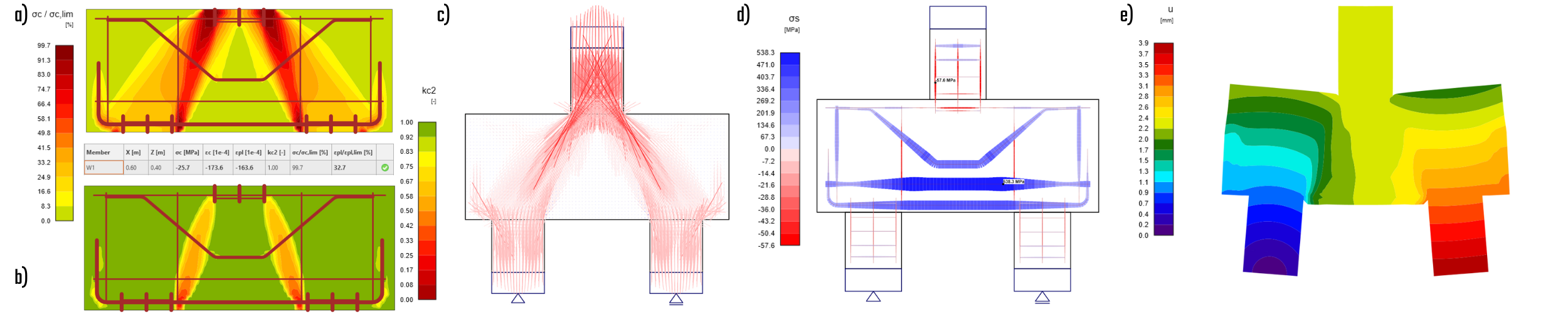
IDEA StatiCa 2D Detail results
The resulting ultimate force for all models is summarized in the table below.
\[ \textsf{\textit{\footnotesize{Fig. 19\qquad CSFM/Experiment utilization }}}\]
In all cases the calculation stops due to concrete failure in the top node of concrete strut. In the following chapters we take a closer look into individual models.
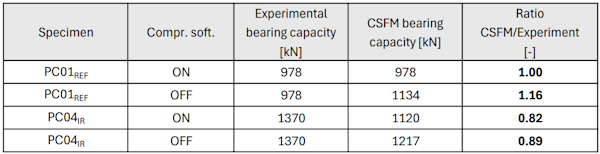
Model PC01REF with compression softening
The ultimate force developed for this model was 978 kN.
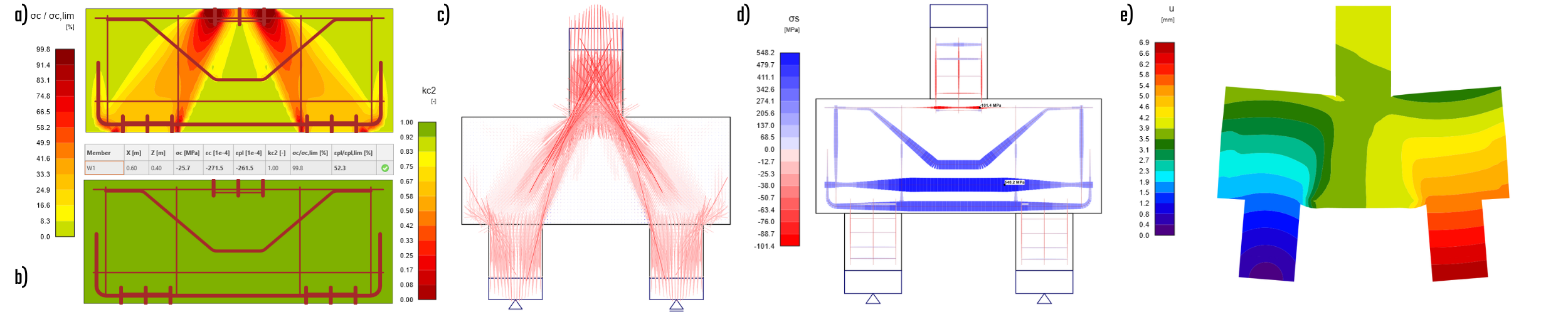
The compression stresses in the column and piles can be disregarded—a material with increased compression strength was defined for these elements to account for the triaxiality. Inside the pile cap, the struts are well apparent. We can see a concentration of principal stresses beneath the column, with the maximum value located in the corner node. In the area above the piles, the stresses are more evenly distributed.
The non-linear calculation stops due to concrete failure in the top node of the concrete strut, which correlates well with the expectations according to the strut-and-tie calculation. The maximum stress in reinforcement can be found on the Ø5mm horizontal stirrup. The stress in the main tensile reinforcement is approximately 342 MPa, again correlating well with the expectations. The value is far from the yield strength of the reinforcement.
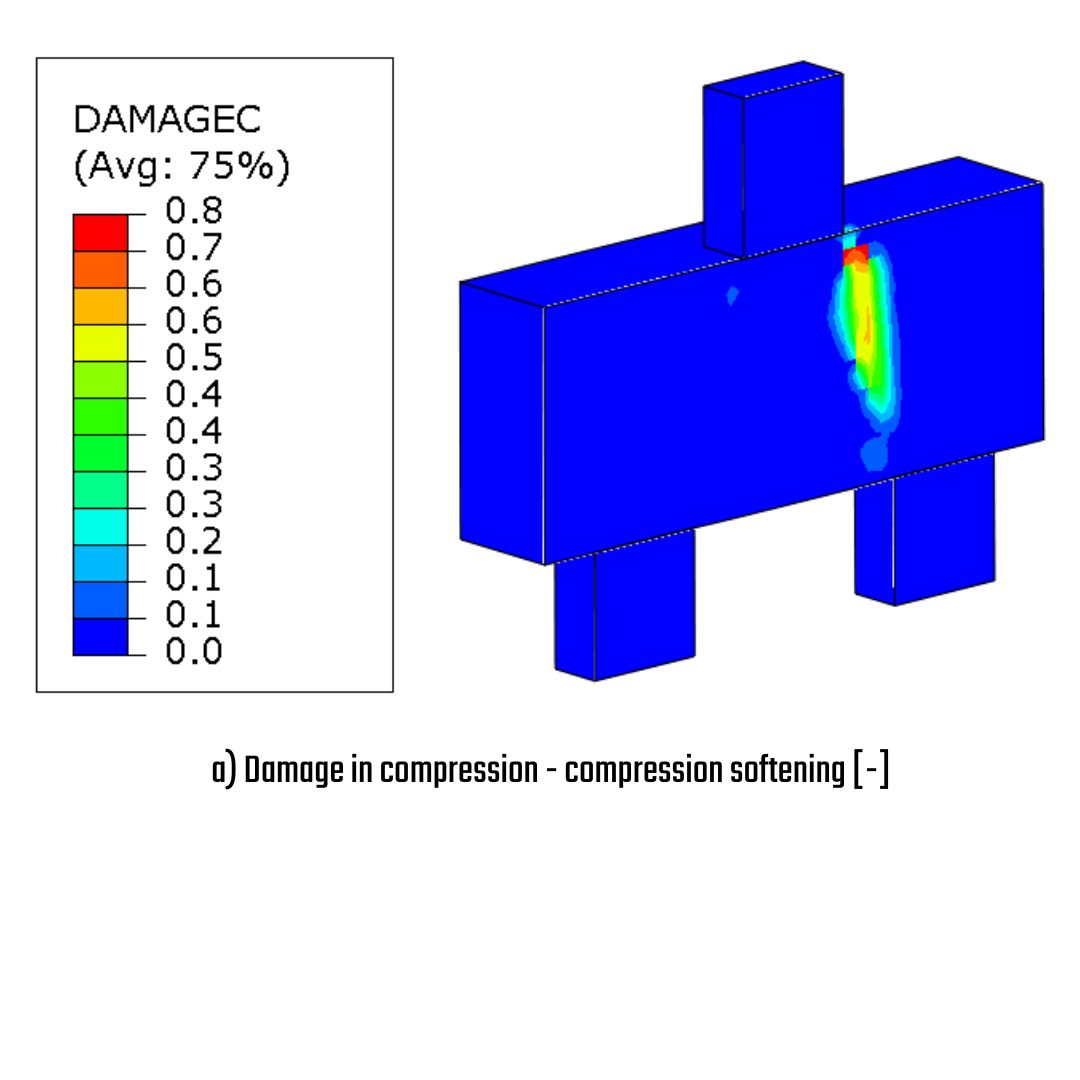
The factor of compression softening applies along the whole strut with the extreme value at the bottom of the pile cap.
\[ \textsf{\textit{\footnotesize{Fig. 20\qquad a) concrete utilization, b) compression softening, c) directions of main stresses, d) stress in reinforcement, e) total deformation }}}\]
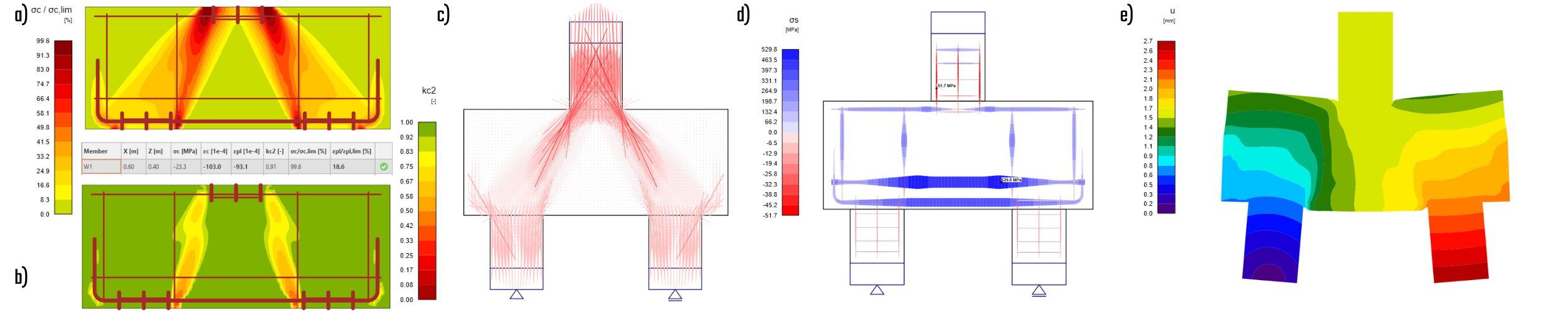
Model PC01REF without compression softening
The ultimate force for this model was 1134 kN, which is about 16% higher than that of the model with compression softening enabled. While the stress distribution patterns are similar, the values achieved are significantly greater. The tensile stress in the main reinforcement bars to approximately 390 MPa, and once again, the failure was due to concrete deterioration.
When compression softening is turned off, the coefficient \( k_{c2} \) is clearly equal to 1.0. In this case, the model exhibits significantly softer behavior, with the maximum total deformation exceeding twice the expected value. The absence of compression softening leads to an overestimation of the experimental threshold, placing the model on the dangerous side, which is unacceptable for structural engineering applications.
\[ \textsf{\textit{\footnotesize{Fig. 21\qquad a) concrete utilization, b) compression softening, c) directions of main stresses, d) stress in reinforcement, e) total deformation }}}\]
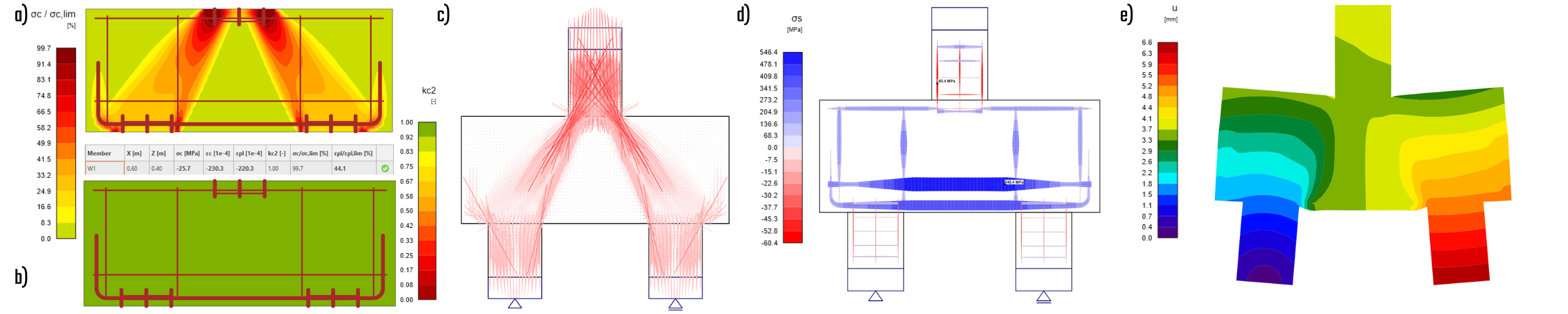
Model PC04IR with compression softening
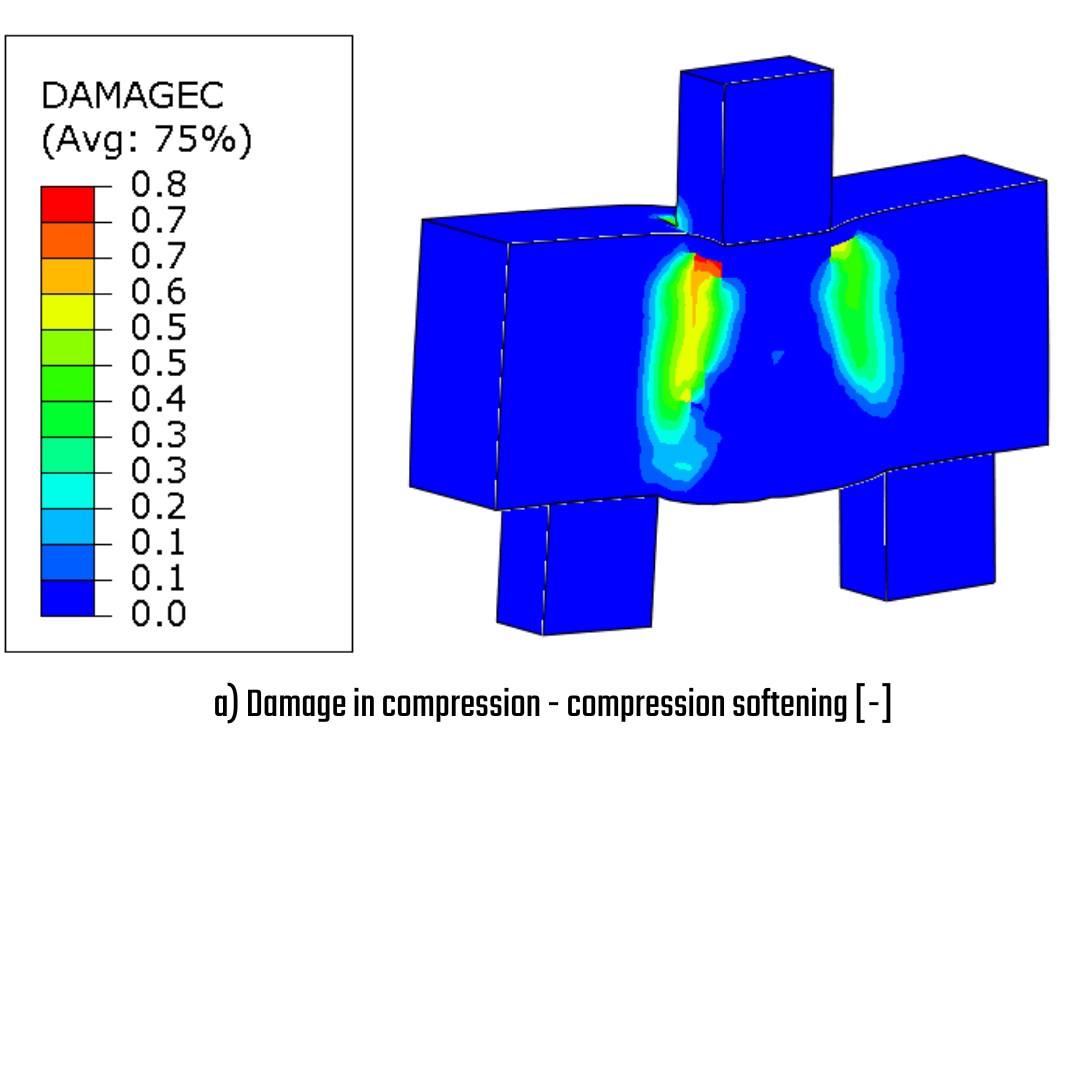
The ultimate force for this model was 1120 kN, which is approximately 15% more than the force observed without the inclined shear reinforcement. It can be noted that while the inclined reinforcement does not reach its full potential utilization, it plays a significant role in widening the compression strut and distributing the compression beneath the column across a larger area.
The following picture illustrates the impact of the additional inclined reinforcement on the compression softening coefficient. With the extra reinforcement, the model achieves a higher total deformation, with a difference of approximately 1 mm.
\[ \textsf{\textit{\footnotesize{Fig. 22\qquad a) concrete utilization, b) compression softening, c) directions of main stresses, d) stress in reinforcement, e) total deformation }}}\]
Model PC04IR without compression softening
The ultimate force for this model was 1217 kN, approximately 9% higher than that of the model with compression softening turned on. We can observe that the influence of compression softening is lower than without the additional reinforcement (there it was 16%).
\[ \textsf{\textit{\footnotesize{Fig. 23\qquad a) concrete utilization, b) compression softening, c) directions of main stresses, d) stress in reinforcement, e) total deformation }}}\]
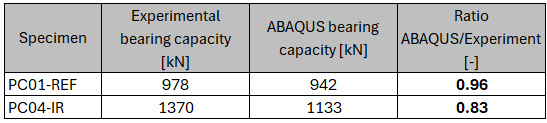
ABAQUS results
The comparison of bearing capacities both experimental setups. The CDP simulation proves agreement between [83-96] % of experimental results.
\[ \textsf{\textit{\footnotesize{Fig. 24\qquad Bearing capacity of experiment/numerical model }}}\]
Model PC01REF
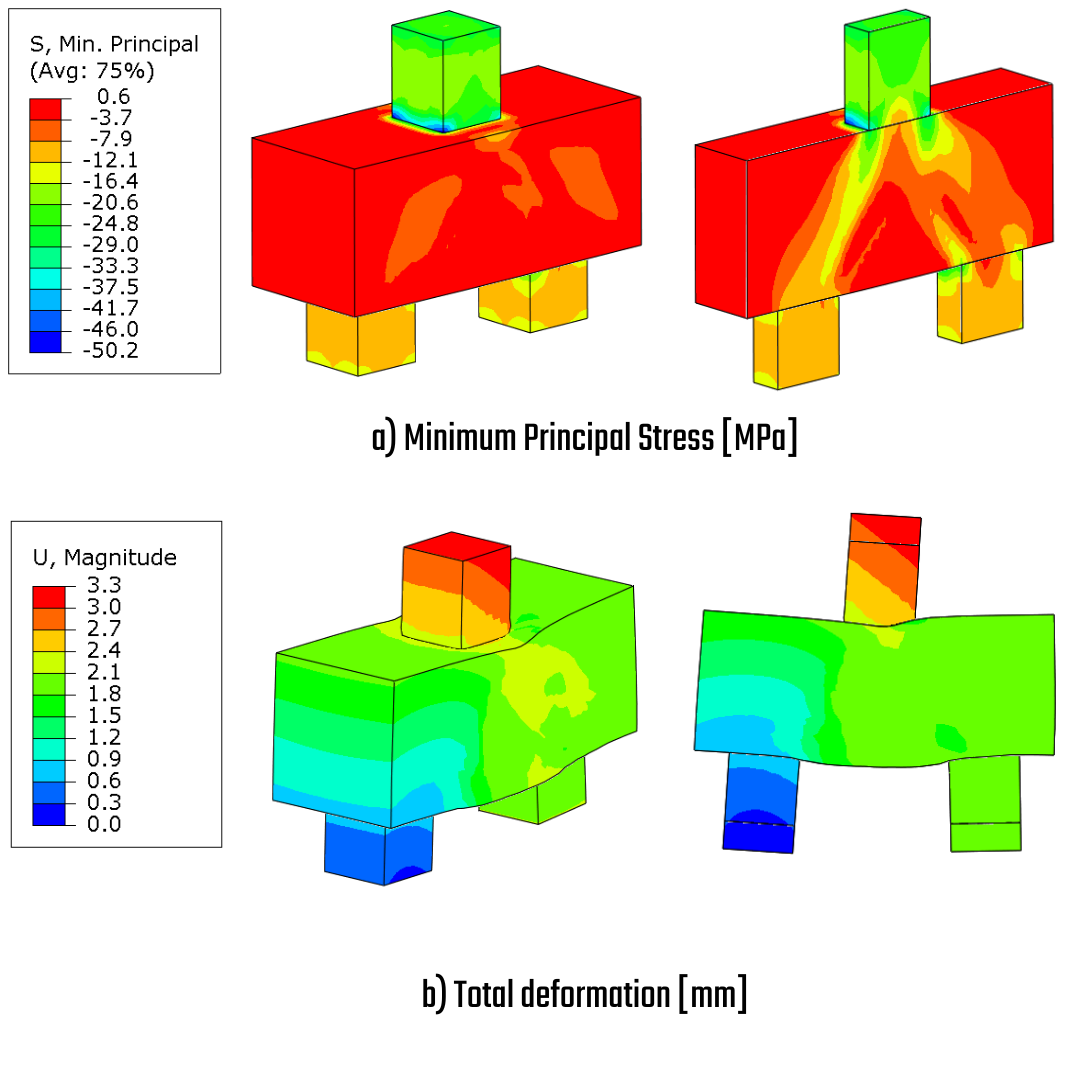
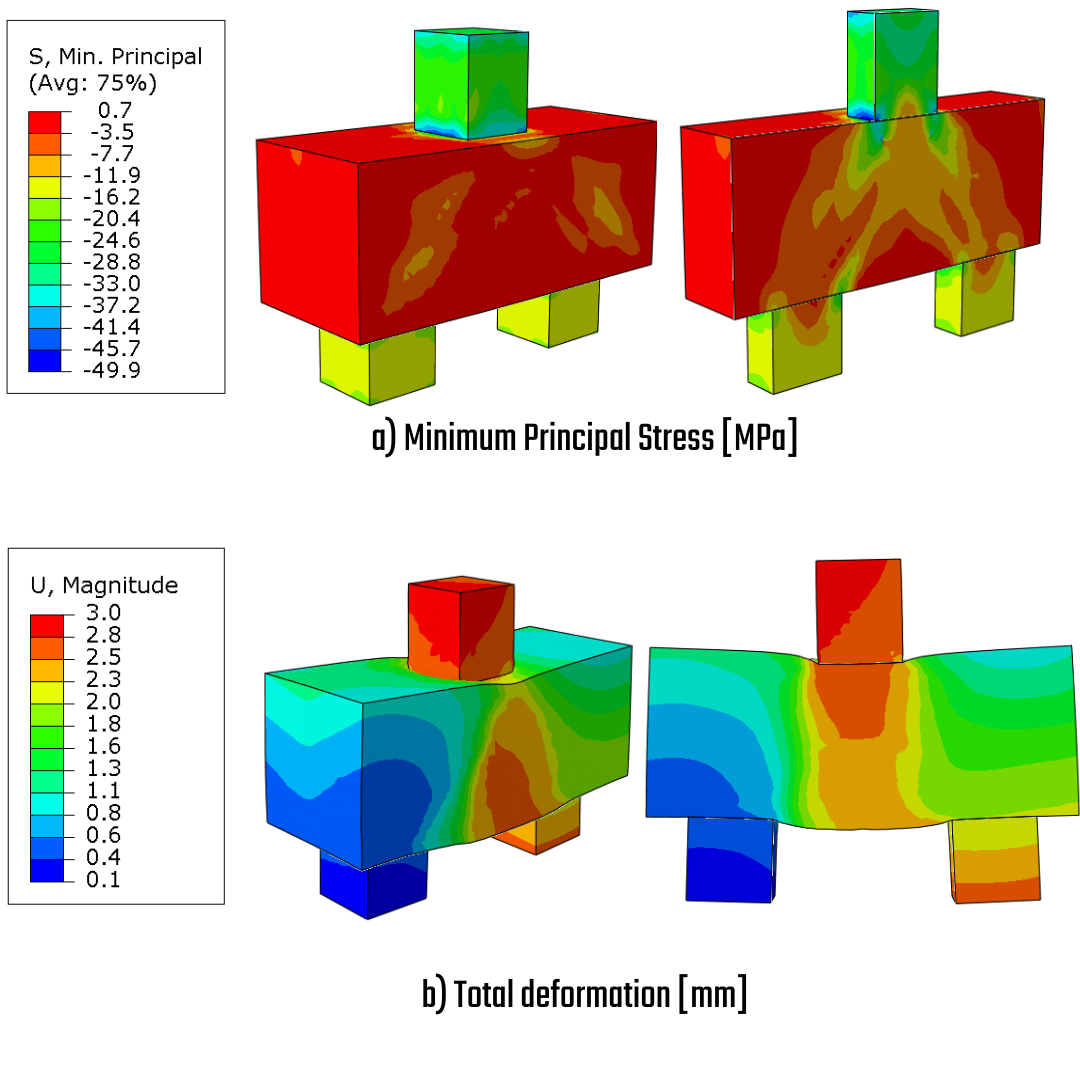
The results are derived from a materially and geometrically nonlinear analysis. The minimum principal stress, Sigma 3, reaches its extreme value at the point where the column transitions into the body of the pile cap. The confinement effect in the column allows for an increase in the stress to -50 MPa. The deformation indicates that the column is punched into the body of the pile cap, and together with the piles, this creates an area of high shear flow.
\[ \textsf{\textit{\footnotesize{Fig. 25\qquad Minimum principal stress, Total deformation}}}\]
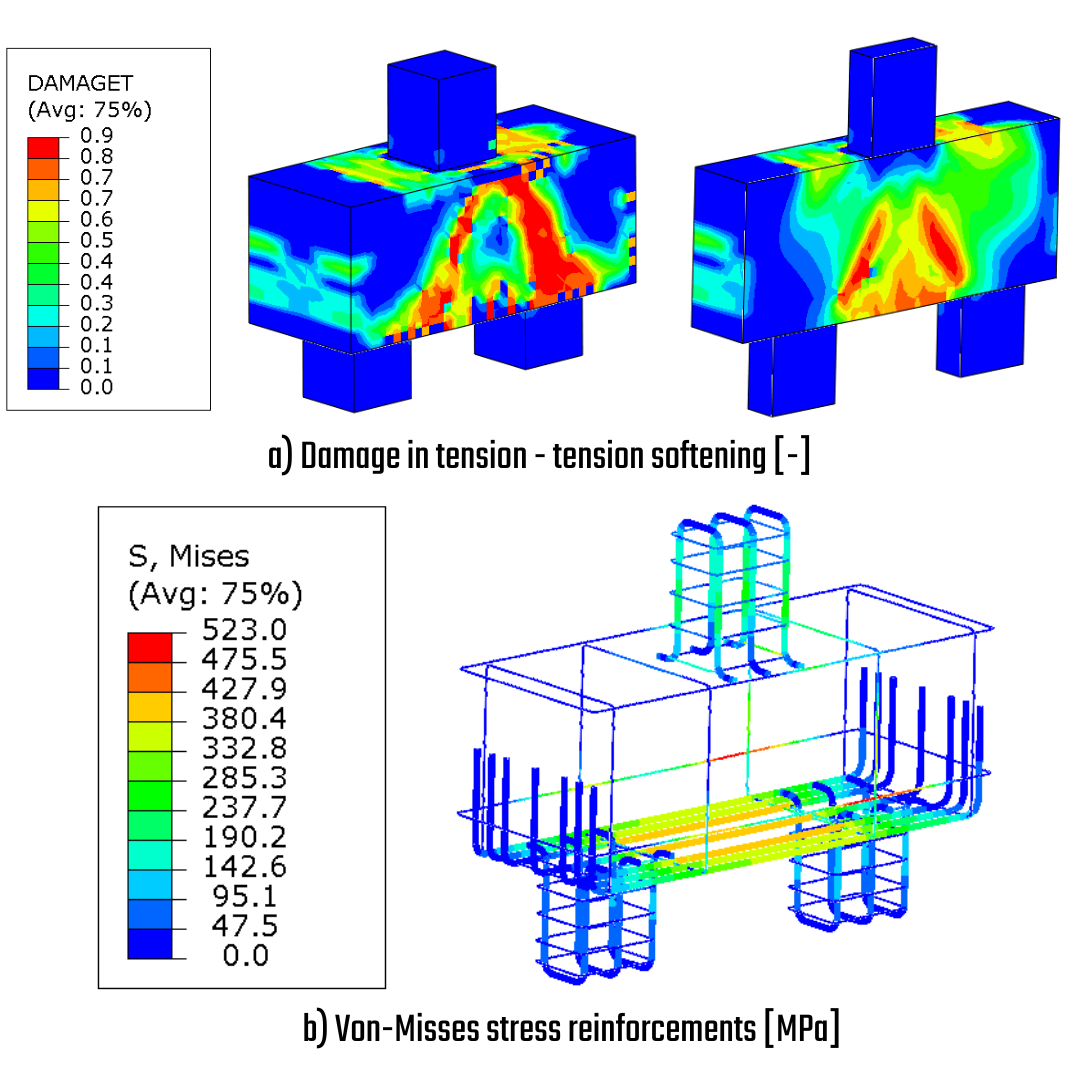
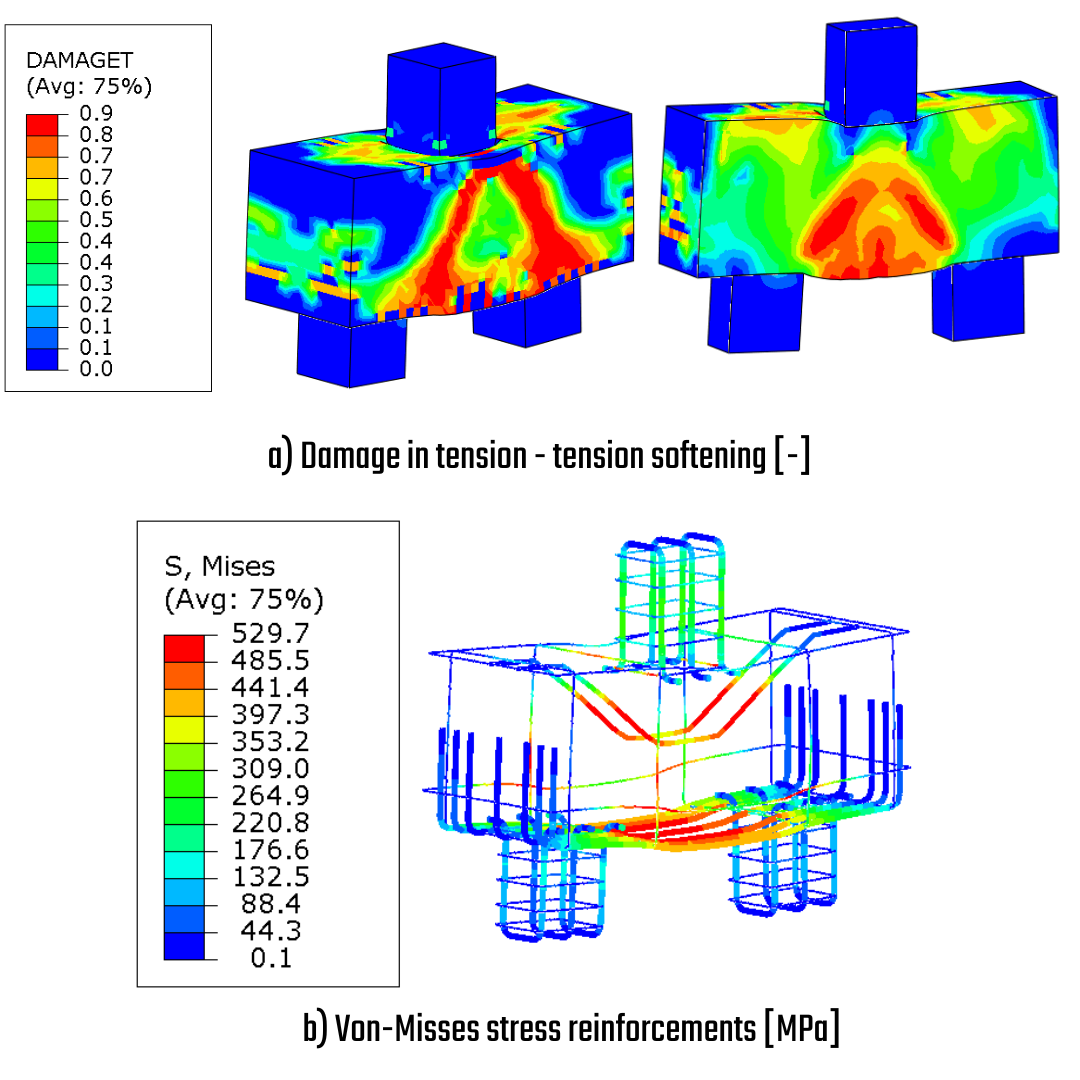
The model includes the tension material diagram and the effect of tension-softening, which is represented through the damage parameter. This parameter is scaled in the range of [0-1], where a value of 1 indicates a complete loss of tensile stiffness, resulting in the exclusion of elements from the simulation. As illustrated in Fig. 17, extreme damage occurs in the area where the crack in the experiment was observed. Additionally, the stress on the reinforcement bars is particularly high in the horizontal stirrups, which strengthen the area of principal tension. The numerical solution affirms the analytical calculation from Fig. 17 and delivers evidence that the failure mode is not on the rebars. The seven bottom tie bars experience a stress of 380 MPa at most.
\[ \textsf{\textit{\footnotesize{Fig. 26\qquad Tension softening, Stress on reinforcement bars}}}\]
The failure mode happened due to excessive shear force, which leads to compression softening and damage in the area of the biggest shear flow. The failure mode corresponds with a real experimental test.
\[ \textsf{\textit{\footnotesize{Fig. 27\qquad Compression softening and failure mode indication}}}\]
Model PC04IR
The model PC04IR with an inclined design exhibits the same minimal principal stress as the previously mentioned model. The stress map shows higher stress levels in the body of the pile cap due to the increased load magnitude compared to model PC01IR. The total deformation observed is 3 mm at the top of the column. This maximum deformation results from the incremental embedding of the column into the body of the pile cap.
\[ \textsf{\textit{\footnotesize{Fig. 28\qquad Minimum principal stress, Total deformation}}}\]
The maximum stress of 530 MPa in the horizontal stirrup indicates the onset of plasticity. However, it's important to note that the main bearing tie bars, with diameters of 12.5 mm and 10 mm, have not yet reached their yield plateau. As observed, the inclined bars have contributed to strengthening the area by significantly enhancing tension softening and overall bearing capacity.
\[ \textsf{\textit{\footnotesize{Fig. 29\qquad Tension softening, Stress on reinforcement bars}}}\]
Due to boundary conditions, the compression softening is asymmetrical. The critical area remains on the side of the horizontally fixed boundary condition. The second side exhibits lower softening due to stress release caused by horizontal movement and the chance of breathing out.
\[ \textsf{\textit{\footnotesize{Fig. 30\qquad Compression softening and failure mode indication}}}\]
Conclusion
This study presents a comprehensive comparison of experimental results, analytical calculations utilizing the Strut-and-Tie Method (STM), and numerical simulations conducted with IDEA StatiCa and ABAQUS to evaluate the structural behavior of reinforced planar concrete pile caps.
Experimentally, specimen PC01REF demonstrated shear failure at a load of 978 kN. In contrast, the incorporation of inclined reinforcement in model PC04IR enhanced the load-bearing capacity to 1370 kN while promoting more uniform cracking patterns. The STM predicted comparable failure mechanisms, thereby validating the effectiveness of the reinforcement without experiencing yielding or failure modes within the concrete strut.
The Compatible Stress Field Model (CSFM) analysis revealed that deactivating compression softening resulted in a 16% increase in the ultimate force for specimen PC01REF, which had a low shear reinforcement ratio. The PC04IR model, which accounted for inclined reinforcement, indicated that the turned-off compression softening resulted in an approximately 11% lower bearing capacity compared to experimental findings. This observation leads to the conclusion that proper shear reinforcement and strengthening in regions where compression softening is predominant can mitigate the effects of this phenomenon.
Conversely, once compression softening is activated, model PC01REF aligns perfectly with experimental data, while model PC04IR exhibits an 18% reduction in bearing capacity, emphasizing the necessity for structural engineers to remain on the conservative side of the design spectrum.
Furthermore, the ABAQUS simulations corroborated the experimental outcomes with an accuracy range of 83% to 96% for model PC04IR and PC01REF, highlighting the failure zones associated with tension softening and confirming the regions of high shear flow. The PC04IR model exhibited superior stress distribution and an enhanced capacity for deformation.
Graph - PC01REF
\[ \textsf{\textit{\footnotesize{Fig. 31\qquad Graph PC01 REF}}}\]
\[ \textsf{\textit{\footnotesize{Fig. 32\qquad Graph PC04 IR}}}\]
In conclusion, the inclined reinforcement significantly improves load capacity and stress distribution. Compression softening is critical in accurately predicting failure, and all models consistently indicate concrete failure as the dominant failure mode.
References
[1] Pile caps with inclined shear reinforcement and steel fibers, Aaron Nzambi, Lana Gomes, Cledinei Amanajás, Francisco Silva, Denio Oliveira, Scientific reports, 2022, https://www.nature.com/articles/s41598-022-14416-2
[2] IDEA StatiCa. (n.d.). Theoretical background for IDEA StatiCa Detail. Retrieved May 30, 2024, from https://www.ideastatica.com/support-center/theoretical-background-for-idea-statica-detail
[3] EN 1992-1-1 Eurocode 2: Design of Concrete Structures—Part I: General Rules and Rules for Buildings. European Committee for Standardization, 2002.
[4] Analysis of nodal stresses in Blévot and Frémy tests, R.G. Delalibera, J.C.G. Silva, J.S. Giongo, A.A.S. Silva, Holos ISSN 1807-1600, 2023
[5] European Committee for Standardization (CEN). EN 1992-1-1:2004: Eurocode 2 – Design of Concrete Structures – Part 1-1: General Rules and Rules for Buildings. December 2004. https://www.phd.eng.br/wp-content/uploads/2015/12/en.1992.1.1.2004.pdf.
[6] ABNT NBR 7480. Specification: Steel for the Reinforcement of Concrete Structures (ABNT, 2007) (in Portuguese).
[7]ABAQUS, Inc. ABAQUS User Subroutines Reference Manual, Version 6.6. Washington University in St. Louis, 2006. https://classes.engineering.wustl.edu/2009/spring/mase5513/abaqus/docs/v6.6/books/usb/default.htm?startat=pt05ch18s05abm36.html.
[8] Massone, L. M.; et al. Shear-Flexure Interaction for Structural Walls, 2006. ResearchGate. https://www.researchgate.net/publication/284079633_Shear-flexure_interaction_for_structural_walls (accessed Jan 01, 2006).