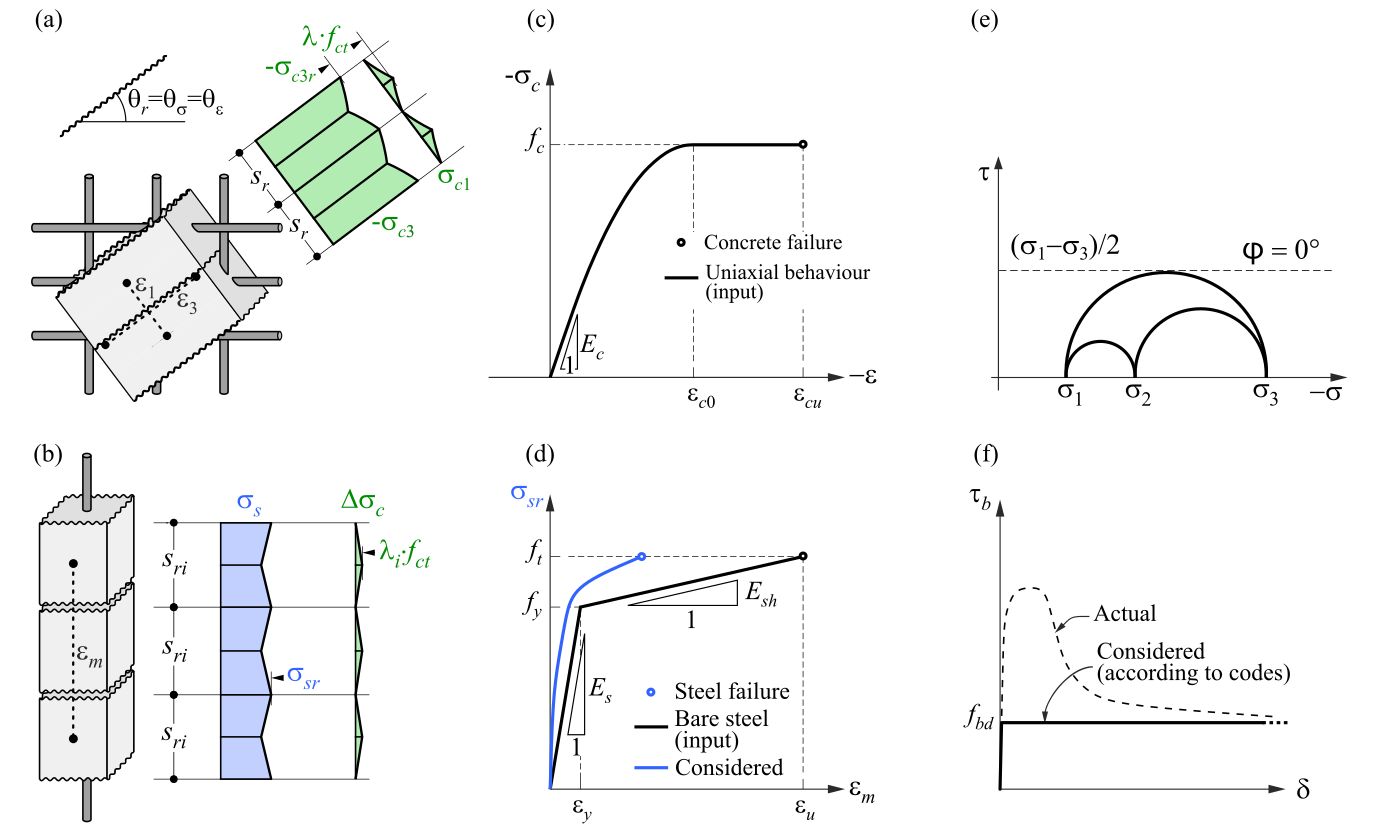
O CSFM 3D define o comportamento do betão com base na teoria da plasticidade de Mohr-Coulomb modificada para cargas monotónicas. O método considera as tensões principais do betão na compressão e as tensões da armadura (σsr) nas fissuras, negligenciando a resistência à tração do betão (corte de tensão), exceto o seu efeito de reforço na armadura (reforço de tensão).
σc1r, σc2r, σc3r ≤ 0 MPa
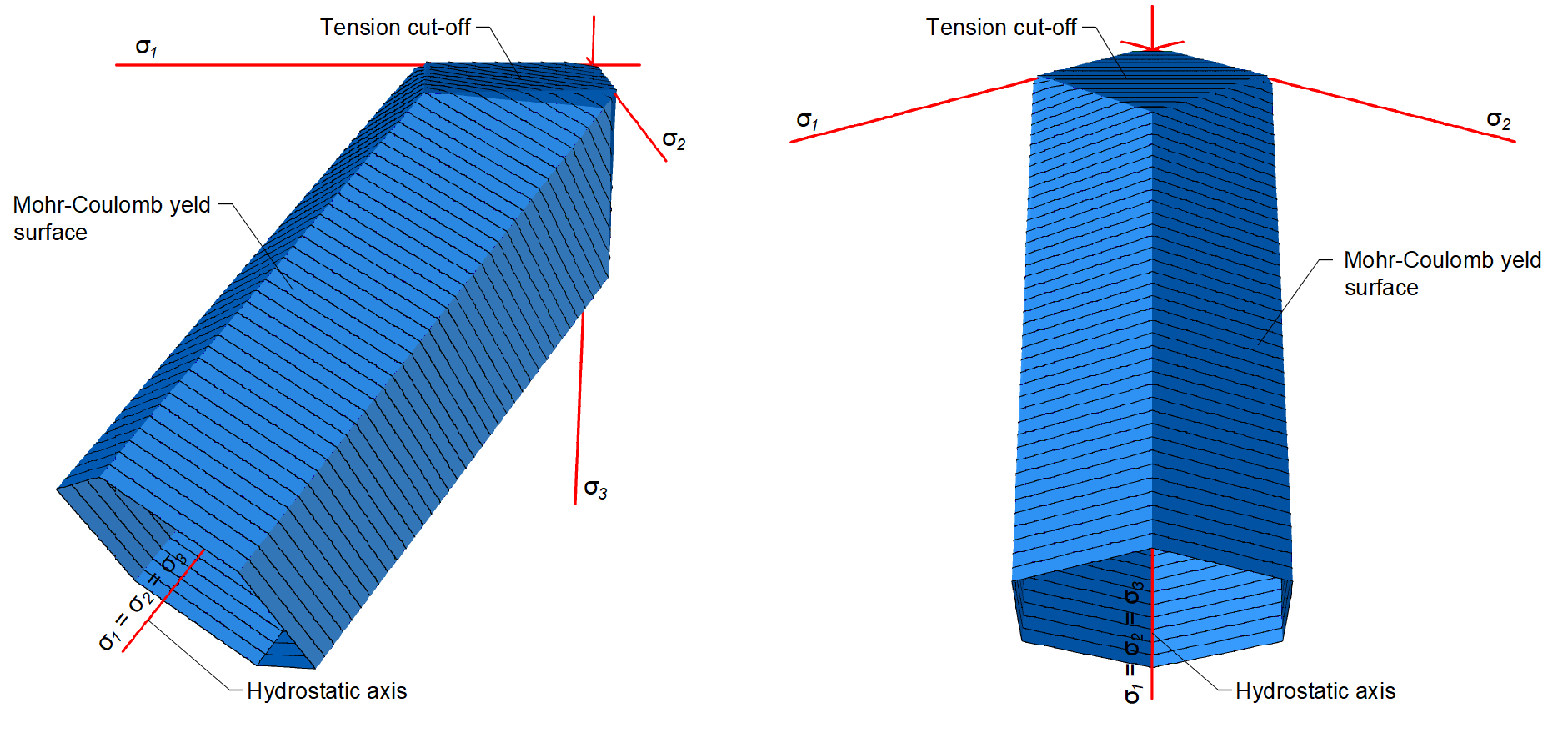
Os varões de reforço estão ligados aos elementos finitos do volume de betão através de elementos de ligação, permitindo o deslizamento entre o betão e o reforço. É de notar que o CSFM 3D não é adequado para simular betão simples devido à ausência de tensão, o que pode resultar em deformações enganadoras e divergência de modelos. De um modo geral, a teoria de Mohr-Coulomb inclui duas propriedades fundamentais que regem a evolução da superfície de plasticidade em compressão e parcialmente em tração: o ângulo de atrito interno φ e o parâmetro de coesão c. O CSFM 3D assume um ângulo de atrito interno nulo (Fig. 1e), conduzindo a um dimensionamento conservador devido à semelhança da superfície de plasticidade com o modelo de Tresca, que é independente do primeiro invariante de tensão.
\( \textsf{\textit{\footnotesize{Fig. 1\qquad Pressupostos básicos do CSFM 3D: (a) tensões principais no betão; (b) tensões na direção da armadura;}}}\) \( \textsf{\textit{\footnotesize{(c) diagrama tensão-deformação do betão em termos de tensões máximas; (d) diagrama tensão-deformação da armadura}}\) \( \textsf{\textit{\footnotesize{em termos de tensões nas fissuras e deformações médias; (e) círculos de Mohr para o modelo de betão em CSFM 3D; (f) tensão de corte da ligação - deslizamento}}\) \( \textsf{\textit{\footnotesize{relação para verificações do comprimento de ancoragem.}}}\)
Betão
O modelo de material apresentado é um modelo de plasticidade multi-superfície dado pela combinação dos modelos de Mohr-Coloumb e Rankine para carregamento monotónico. É importante notar que este modelo não aborda a descarga, pelo que as variáveis de estado não são armazenadas, como seria o caso nos modelos clássicos de plasticidade utilizados para cargas cíclicas.
\[ \textsf{\textit{\footnotesize{Fig. 2\qquad Mohr-Coulomb multi-surface plasticity model for friction angle 0 degree}}}\]
Como já foi referido, o modelo de material destina-se a ser utilizado em aplicações que calculam a resposta do betão armado (não é adequado para betão simples). Isto deve-se à exclusão do betão em tração. Por conseguinte, o modelo nem sequer é adequado para elementos estruturais em que as regras de dimensionamento do betão armado, tais como a taxa de armadura mínima, o espaçamento máximo entre barras, etc., não são cumpridas. Deve também ser acrescentado que, por razões de estabilidade numérica, é definida uma capacidade de tração muito pequena no modelo. A parte de tração é limitada por planos correspondentes ao modelo de Rankine.
O modelo CSFM 3D no IDEA StatiCa Detail não considera um critério de rotura explícito em termos de deformações para o betão em compressão (ou seja, considera um ramo infinitamente plástico após a tensão de pico ser atingida). Esta simplificação não permite a verificação da capacidade de deformação das estruturas que roem à compressão. No entanto, a sua capacidade última é corretamente prevista quando o aumento da fragilidade do betão à medida que a sua resistência aumenta é considerado através do fator de redução𝜂𝑓𝑐 definido no fib Model Code 2010 da seguinte forma:
\[f_{c,red} = \eta _{fc} \cdot f_{c}\]
\[{\eta _{fc}} = {\left( {\frac{{{30}}}{{{f_{c}}}}} \right)^{\frac{1}{3}}} \le 1\]
onde:
fc é a resistência caraterística do cilindro de betão (em MPa para a definição de \ ( \eta_{fc} \)).
A fc,red é então comparada com a Tensão Principal Equivalente σc,eq no betão, que será definida mais tarde, naturalmente, com a consideração de todos os factores de segurança prescritos pelo código.
Uma descrição detalhada do modelo de betão pode ser encontrada na seguinte ligação:
Reforço
O diagrama bilinear tensão-deformação para varões de armadura, tal como definido pelos códigos de projeto (Fig. 1d), representa um modelo idealizado. Este modelo requer o conhecimento das propriedades básicas da armadura durante a fase de projeto, especificamente a classe de resistência e ductilidade. Em alternativa, os utilizadores têm a opção de definir uma relação tensão-deformação personalizada.
A rigidez à tração é considerada através da modificação da relação tensão-deformação do varão de reforço nu para captar a rigidez média dos varões embebidos no betão (εm) (Fig. 1b).
Ancoragem
O deslizamento da ligação entre a armadura e o betão é introduzido no modelo de elementos finitos considerando a relação constitutiva simplificada rígida-perfeitamente plástica apresentada na (Fig. 1f), sendo fbd o valor de projeto (valor facturado) da tensão última da ligação especificada pelo código de projeto para as condições específicas da ligação.
Este é um modelo simplificado com o único objetivo de verificar as prescrições de ligação de acordo com os códigos de projeto (i.e., ancoragem do reforço). A redução do comprimento de ancoragem quando se utilizam ganchos, laços e formas de barra semelhantes pode ser considerada através da definição de uma determinada capacidade na extremidade da armadura, como será descrito mais adiante.
Ancoragens
O elemento da ancoragem é definido como sendo capaz de transferir forças normais de tração ou compressão, bem como forças de corte, considerando também a rigidez à flexão. No entanto, apenas é avaliada a tensão normal nas ancoragens.
Estão disponíveis dois tipos de ancoragens:
- Ancoragem adesiva
- Reforço no local
O comportamento da armadura de betão armado é o mesmo que o da armadura clássica (tipo de ancoragem, ligação, etc.) . Para as ancoragens adesivas, é possível definir diretamente o valor de projeto da resistência da ligação. Este valor deve ser lido na ficha técnica do fabricante.