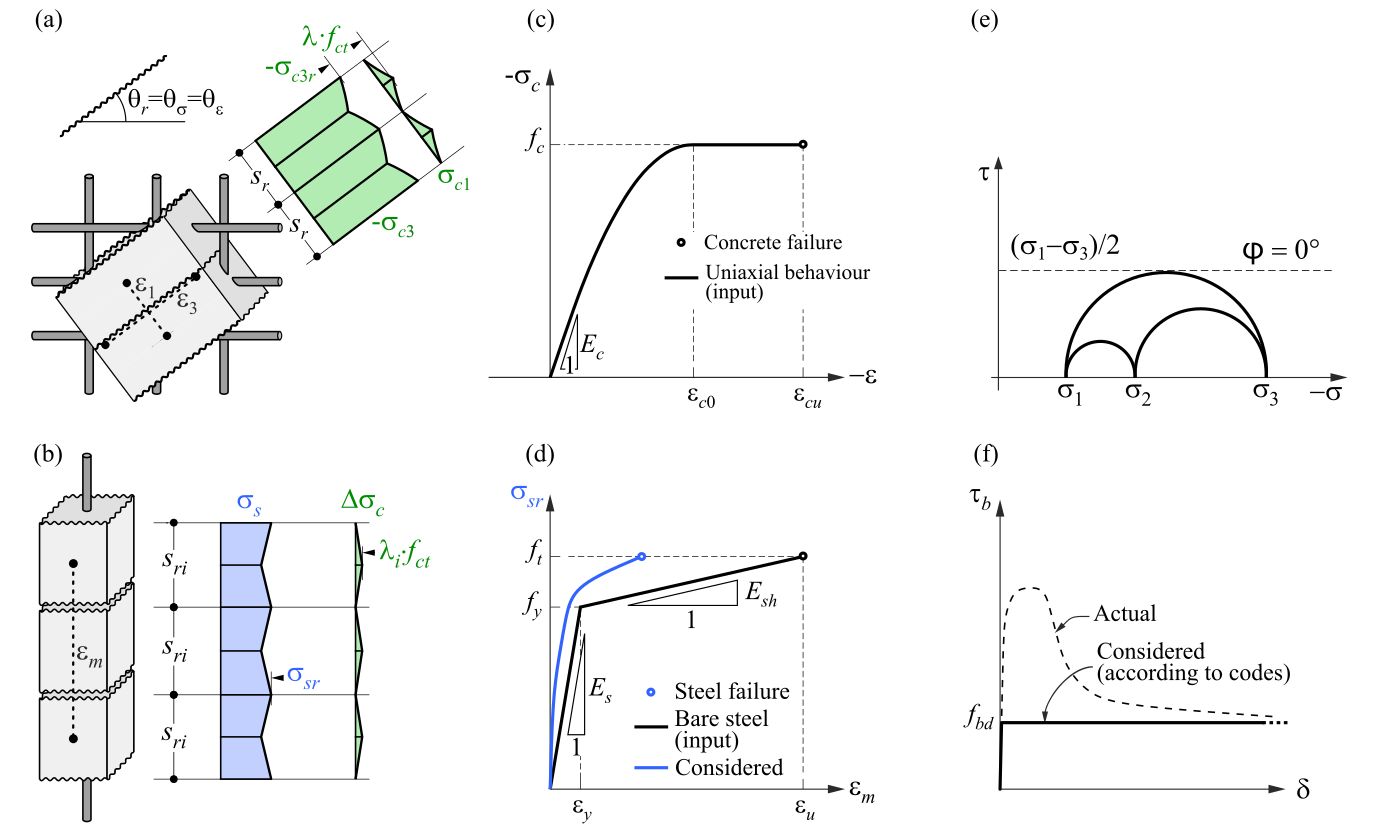
3D CSFM definiert das Betonverhalten auf der Grundlage der modifizierten Mohr-Coulomb-Plastizitätstheorie für monotone Belastung. Die Methode berücksichtigt die Hauptdruckspannungen des Betons und die Betonstahlspannungen (σsr) an den Rissen und vernachlässigt die Zugfestigkeit des Betons, mit Ausnahme der Mitwirkung des Beton Zwischen den Rissen (Zugaussteifung).
σc1r, σc2r, σc3r ≤ 0 MPa
Die Bewehrungsstäbe sind mit den finiten Elementen des Betonvolumens durch Verbundelemente verbunden, die ein Gleiten zwischen Beton und Bewehrung ermöglichen. Es ist zu beachten, dass die 3D-CSFM nicht für die Simulation von unbewehrtem Beton geeignet ist. Im Allgemeinen umfasst die Mohr-Coulomb-Theorie zwei grundlegende Eigenschaften, die die Entwicklung der Plastizitätsfläche unter Druck und teilweise unter Zug bestimmen: den inneren Reibungswinkel φ und den Kohäsionsparameter c. 3D CSFM geht von einem inneren Reibungswinkel von Null aus (Abb. 1e), was zu einer konservativen Bemessung führt.
\( \textsf{\textit{\footnotesize{Abb. 1\qquad Grundannahmen des 3D CSFM: (a) Hauptspannungen im Beton; (b) Spannungen in Bewehrungsrichtung;}}}\) \( \textsf{\textit{\footnotesize{(c) Spannungs-Dehnungs-Diagramm des Betons in Form von maximalen Spannungen; (d) Spannungs-Dehnungs-Diagramm}}}\) \( \textsf{\textit{\footnotesize{des Betonstahls in Form von Spannungen an Rissen und mittleren Dehnungen; (e) Mohrsche Kreise für Betonmodell in 3D CSFM; }}}\) \( \textsf{\textit{\footnotesize{(f) Verbund Schubspannung-Schlupf-Beziehung für Verankerungslängennachweise.}}}\)
Beton
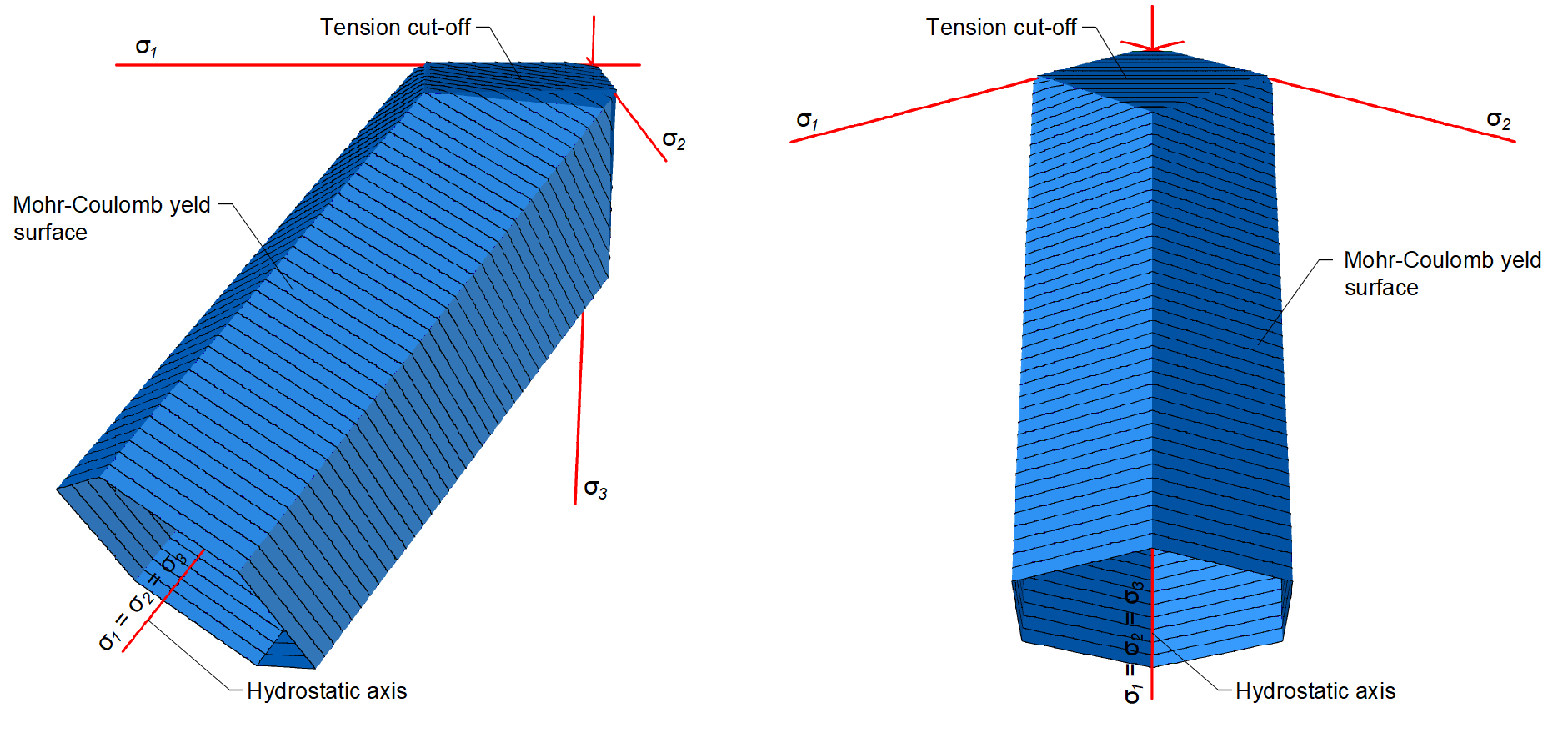
Das vorgestellte Materialmodell ist ein Mehrflächenplastizitätsmodell, das durch die Kombination des Mohr-Coloumb- und des Rankine-Modells für monotone Belastung gegeben ist. Es ist wichtig zu beachten, dass dieses Modell keine Entlastung berücksichtigt, wie es bei klassischen Plastizitätsmodellen für zyklische Belastung der Fall wäre.
\[ \textsf{\textit{\footnotesize{Abb. 2\qquad Mohr-Coulomb-Mehrflächenplastizitätsmodell für den Reibungswinkel 0 Grad}}}\]
Wie bereits erwähnt, ist das Materialmodell für Anwendungen von bewehrtem Beton gedacht. Dies ist auf die Vernachlässigung von Beton unter Zug zurückzuführen. Daher ist das Modell nicht einmal für Bauteile geeignet, bei denen die Bemessungsregeln für Stahlbeton, wie Mindestbewehrungsgrad, maximaler Stababstand usw., nicht erfüllt sind. Es sollte auch hinzugefügt werden, dass aus Gründen der numerischen Stabilität eine sehr kleine Zugkapazität im Modell definiert ist. Der Zugteil wird durch Ebenen begrenzt, die dem Rankine-Modell entsprechen.
3D CSFM in IDEA StatiCa Detail berücksichtigt kein explizites Versagenskriterium in Form von Dehnungen für Beton unter Druck (d.h. es wird ein unendlich plastischer Zweig nach Erreichen der Spitzenspannung betrachtet). Durch diese Vereinfachung kann die Verformungskapazität von Bauwerken, die auf Druck versagen, nicht nachgewiesen werden. Ihre Tragfähigkeit wird jedoch richtig vorhergesagt, wenn die Zunahme der Sprödigkeit des Betons bei steigender Festigkeit mit Hilfe des im fib Model Code 2010 wie folgt definierten Abminderungsfaktors 𝜂𝑓𝑐 berücksichtigt wird:
\[f_{c,red} = \eta _{fc} \cdot f_{c}\]
\[{\eta _{fc}} = {\left( {\frac{{30}}{{{f_{c}}}}} \right)^{\frac{1}{3}}} \le 1\]
wobei:
fc die charakteristische Festigkeit des Betonzylinders ist (in MPa für die Definition von \ ( \eta_{fc} \)).
fc,red wird dann mit der äquivalenten Hauptspannung σc,eq im Beton verglichen, die natürlich unter Berücksichtigung aller in den Normen vorgeschriebenen Sicherheitsfaktoren weiter definiert wird.
Eine detaillierte Beschreibung des Betonmodells finden Sie unter dem folgenden Link:
Bewehrung
Das bilineare Spannungs-Dehnungs-Diagramm für Bewehrungsstäbe, wie es in den Bemessungsregeln definiert ist (Abb. 1d), stellt ein idealisiertes Modell dar. Dieses Modell setzt die Kenntnis der grundlegenden Eigenschaften der Bewehrung während der Bemessungsphase voraus, insbesondere der Festigkeits- und Duktilitätsklasse. Alternativ kann der Anwender auch eine individuelle Spannungs-Dehnungs-Beziehung definieren.
Die Mitwirkung des Betons zwischen den Rissen (Tension Stiffening) wird berücksichtigt, indem die Spannungs-Dehnungs-Beziehung des "nackten" Bewehrungsstabs modifiziert wird, um die durchschnittliche Steifigkeit der im Beton eingebetteten Stäbe (εm) zu erfassen (Abb. 1b).
Verankerung
Der Verbundschlupf zwischen der Bewehrung und dem Beton wird in das Finite-Elemente-Modell aufgenommen, indem die vereinfachte starr-perfektplastische Beziehung in (Abb. 1f) berücksichtigt wird, wobei fbd der Bemessungswert (faktorisierter Wert) der Verbundspannung ist, der in der Bemessungsvorschrift für die spezifischen Verbundbedingungen angegeben ist.
Es handelt sich hierbei um ein vereinfachtes Modell, das ausschließlich dem Zweck dient, die in den Bemessungsvorschriften vorgeschriebenen Verbundspannungen (d. h. die Verankerung der Bewehrung) zu berücksichitgen. Die Reduzierung der Verankerungslänge bei der Verwendung von Haken, Schlaufen und ähnlichen Stabformen kann durch die Definition einer bestimmten Kapazität am Ende der Bewehrung berücksichtigt werden, wie weiter unten beschrieben wird.
Verankerungen
Das Ankerelement ist so definiert, dass es sowohl normale Zug- oder Druckkräfte als auch Querkräfte übertragen kann, wobei auch die Biegesteifigkeit der Anker berücksichtigt wird. Es wird jedoch nur die Normalspannung in den Ankern bewertet.
Es gibt zwei Arten von Ankern:
- Chemische Anker
- Betonstahlanker
Die Betonstahlanker verhalten sich wie die klassische Bewehrung (Verankerungsart, Verbund, usw.). Bei chemischen Ankern kann der Bemessungswert Verbundfestigkeit direkt definiert werden. Dieser Wert sollte aus dem technischen Datenblatt des Herstellers bzw. Zulassung entnommen werden.