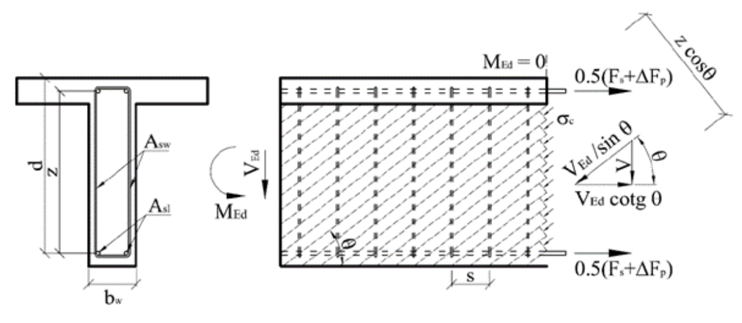
Interação da força de corte e da torção para armaduras de corte
Determinação da força na armadura de corte devido à força de corte.
O cálculo baseia-se na fórmula de cálculo da resistência da armadura de corte definida na EN 1992-1-1. Com base na equação 6.13 (cap. 6.2.3 (4)), a resistência à carga de uma perna de estribo pode ser derivada como:
\[{{V}_{Rd,s}}=\frac{{{A}_{sw,V}}}{s}z{{{f}_{ywd}}\left( \cot \theta +\cot \alpha \right)\sin \alpha \cos \beta \]
\[\frac{{{A}_{sw,V}}}{s}={{a}_{sw,V}}\]
Asw,V. . . área da secção transversal de uma perna do estribo que resiste ao corte na secção considerada
s . . . . . espaçamento da armadura de corte na direção do eixo longitudinal da barra
asw,V. . . . área da secção transversal da armadura de corte por unidade de comprimento
z . . . . . o braço de alavanca interior. Para uma barra com profundidade constante, correspondente ao momento fletor no elemento em consideração. Na análise de corte do betão armado sem força axial, o valor aproximado z = 0,9d pode ser normalmente utilizado.
fywd. . . a tensão de cedência de projeto da armadura de corte
θ . . . . . o ângulo entre a escora de compressão do betão e o eixo da barra perpendicular à força de corte
α . . . . . o ângulo entre a armadura de cisalhamento e o eixo da barra perpendicular à força de cisalhamento
β . . . . . inclinação da perna do estribo em relação à resultante da força de corte aplicada
A força de corte é redistribuída uniformemente entre as armaduras individuais que resistem à força de corte com base no ângulo da armadura e na rigidez axial das pernas individuais do estribo.
\[{{V}_{ed}}={{V}_{ed,1}}+{{V}_{ed,2}}+...+{{V}_{ed,n}}\]
\[{{V}_{ed}}={{\varepsilon }_{sw,V}}\cdot z\cdot \sum\limits_{i=1}^{{{n}_{V}}}{{{a}_{sw,i,V}}\cdot {{E}_{sw,i,V}}\cdot \left( \cot \theta +\cot {{\alpha }_{i}} \right)\cdot {{\cos }^{2}}{{\beta }_{i}}}\]
Além disso, a deformação média da armadura considerada na direção da força de corte resultante pode ser derivada:
\[{{\varepsilon }_{sw,V}}=\frac{{{V}_{ed}}}{z\cdot \sum\limits_{i=1}^{{{n}_{V}}}{{{a}_{sw,i,V}}\cdot {{E}_{sw,i,V}}\cdot \left( \cot \theta +\cot {{\alpha }_{i}} \right)\cdot {{\cos }^{2}}{{\beta }_{i}}}}\]
A deformação efectiva da i-ésima armadura pode ser calculada como:
\[{{\varepsilon }_{sw,i,V}}=\frac{{{\varepsilon }_{sw,V}}}{\sin {{\alpha }_{i}}}\cdot \cos {{\beta }_{i}}\]
A tensão numa determinada perna da armadura:
\[{{\sigma }_{sw,i,V}}={{\varepsilon }_{sw,i,V}}\cdot {{E}_{si,V}}\]
Determinação da força num estribo individual devido à torção
A resistência à torção de uma secção pode ser calculada com base numa secção fechada de parede fina, na qual o equilíbrio é satisfeito por um fluxo de corte fechado. As secções sólidas podem ser modeladas por secções de parede fina equivalentes. Para secções não sólidas, a espessura da parede equivalente não deve exceder a espessura real da parede.
O fluxo de cisalhamento nas paredes de uma secção fechada de parede fina devido à torção pode ser calculado como:
\[{{\tau }_{t}}\cdot {{t}_{ef}}=\frac{{{T}_{ed}}}{2{{A}_{k}}}\]
A força de corte numa determinada parede é então:
\[{{V}_{i}}={{\tau }_{t}}\cdot {{t}_{ef}}\cdot {{l}_{i}}\]
li. . . . comprimento da linha de centro do muro em consideração
Força de corte na alma - o comprimento da linha central da alma pode ser substituído pelo valor do braço de alavanca "z".
\[{{V}_{ed,T}}=\frac{{{T}_{ed}}}{2{{A}_{k}}}\cdot z\]
Força nos estribos que resiste à torção por um metro de comprimento da barra (por unidade de comprimento):
\[{{F}_{sw,T}}=\frac{{{V}_{ed,T}}}{z\cdot \cot \theta }=\frac{{{T}_{ed}}}{2{{A}_{k}}}\cdot tg\theta\]
Decomposições de forças para estribos individuais
Se for definido o mesmo material para todos os estribos, a tensão resultante devido à torção em cada perna do estribo é constante. Então:
\[{{\sigma }_{sw,T}}=\frac{{{F}_{sw,T}}}{{{a}_{sw,T}}}\]
em queasw,T é a área total dos estribos que resistem à torção por unidade de comprimento.
No caso de os estribos individuais terem materiais diferentes, a rigidez axial das barras individuais deve ser tida em conta.
\[{{F}_{sw,T}}={{F}_{s1,T}}+{{F}_{s2,T}}+{{F}_{s3,T}}+...+{{F}_{sn,T}}=\sum\limits_{i=1}^{{{n}_{T}}}{{{F}_{si,T}}}\]
\[{{\varepsilon }_{sw,T}}=\frac{{{F}_{sw,T}}}{\sum\limits_{i=1}^{{{n}_{T}}}{\left( {{a}_{si,T}}\cdot {{E}_{si,T}} \right)}}\]
nT. . . . . número de pernas de armadura (grupos de armadura) que resistem à torção
Fsi,T. . . força no i-ésimo grupo de armadura resultante da torção por unidade de comprimento
asi,T. . . área da secção transversal da armadura de corte que resiste à torção por unidade de comprimento
Esi,T. . . módulo de elasticidade de Young do i-ésimo grupo de armaduras resistentes à torção
εsw,T. . deformação na armadura devido à torção
A tensão resultante em cada estribo devido à torção aplicada é calculada como:
\[{{\sigma }_{sw,i,T}}={{\varepsilon }_{sw,T}}\cdot {{E}_{si,T}}\]
Interação V+T
O cálculo das tensões nos estribos devido ao corte e à torção é então uma soma das tensões devidas a componentes de carga individuais.
\[{{\sigma }_{sw,i}}={{{\sigma }_{sw,i,V}}+{{\sigma }_{sw,i,T}}\]
Força resultante na i-ésima armadura:
\[{{F}_{sw,i}}={{{a}_{sw,i}}\cdot {{\sigma }_{sw,i}}\]
Interação de corte, torção e flexão para armadura longitudinal
Determinação da força em cada armadura longitudinal devido à força normal e ao momento fletor
A aplicação RCS é utilizada para calcular a resposta da secção transversal devido à combinação da força normal e do momento fletor para determinar a tensão e a deformação nos varões longitudinais individuais e na armadura de pré-esforço.
Determinação da força na armadura longitudinal individual devido à força de corte
O incremento da força de tração na armadura longitudinal ΔFtd a partir da força de corte depende da geometria do modelo de escora e tirante.
\[\ Delta {{F}_{td}}={{{V}_{ed}}}\left( \cot \theta -\cot \alpha \right)\]
ΔFtd. . . incremento da força de tração na armadura longitudinal devido à força de corte
Ved. . . . valor de projeto da força de corte que actua na secção em consideração
θ . . . . . o ângulo entre a escora de compressão de betão e o eixo da barra
α . . . . . o ângulo entre a armadura de corte e o eixo da barra
Para a armadura longitudinal situada na corda de tração, a força resultante Ft na armadura longitudinal devido à combinação N+M+V não deve ser superior aMEd,max/z(ondeMEd,max é o momento máximo ao longo da viga)
\[{{F}_{t}}=\frac{{{M}_{Ed}}}{z}+0,5{{V}_{ed}}\left( \cot \theta -\cot \alpha \right)\le \frac{{{M}_{Ed,\max }}}{z}\]
A força ΔFtd é transmitida por todos os tendões de pré-esforço ligados e armaduras localizadas na parte da secção que resiste ao corte (a alma no caso de um perfil em I). Por segurança, a contribuição da armadura de pré-esforço pode ser considerada 0. O pressuposto do cálculo é que o incremento da deformação axial da armadura longitudinal individual que resiste ao corte é constante (Δεs1,V = Δεs2,V = .... =Δεp1,V = Δεp2,V = ... = ΔεV = const.). A derivação é válida para um diagrama de trabalho de armadura bilinear com um ramo plástico horizontal. No caso de um diagrama com um ramo inclinado, o cálculo deve ser modificado.
\[\Delta {{F}_{td}}=\Delta {{F}_{s}}+\Delta {{F}_{s}}\]
\[\Delta {{F}_{td}}=\Delta {{\varepsilon }_{V}}\cdot \sum\limits_{i=1}^{{{n}_{s,V}}}{{{A}_{sl,i,V}}\cdot {{E}_{sl,i,V}}}+\Delta {{\varepsilon }_{V}}\cdot \sum\limits_{i=1}^{{{n}_{p,V}}}{{{A}_{pl,i,V}}\cdot {{E}_{pl,i,V}}}\]
ΔεV. . . . incremento de deformação na armadura longitudinal devido à força de corte
ns,V. . . . número de armaduras longitudinais que resistem à força de corte
Asl,i,V. . . . área da i-ésima armadura longitudinal que resiste à força de corte
Esl,i,V. . . . módulo de elasticidade de Young da i-ésima armadura longitudinal que resiste à força de corte
np,V. . . . número de tendões que resistem à força de corte
Apl,i,V. . . . área do i-ésimo tendão que resiste à força de corte
Epl,i,V. . . . módulo de elasticidade de Young do i-ésimo tendão que resiste à força de corte
Após determinar o valor da força ΔFtd, a deformação média da armadura ΔεV pode então ser calculada.
\[\Delta {{\varepsilon }_{V}}=\frac{\Delta {{F}_{td}}}{\sum\limits_{i=1}^{{{n}_{s,V}}}{{{A}_{sl,i,V}}\cdot {{E}_{sl,i,V}}}+\sum\limits_{i=1}^{{{n}_{p,V}}}{{{A}_{pl,i,V}}\cdot {{E}_{pl,i,V}}}}\]
Incremento de tensão nas barras longitudinais individuais devido à força de corte aplicada:
para vergalhões \[\Delta {{\sigma }_{sl,i,V}}=\Delta {{\varepsilon }_{V}}\cdot {{E}_{sl,i,V}}\]
para o tendão \[\Delta {{\sigma }_{pl,i,V}}=\Delta {{\varepsilon }_{V}}\cdot {{E}_{pl,i,V}}\]
Determinação da força em cada armadura longitudinal a partir da torção
É muito importante determinar a armadura longitudinal que resiste à torção. Estas são as armaduras que estão localizadas numa secção de parede fina eficaz alternativa resistente à torção.
\[\frac{\sum{{{A}_{sl}}{{f}_{yd}}}}{{{u}_{k}}}=\frac{{{T}_{ed}}}{2{{A}_{k}}}\cot \theta \]
De acordo com a norma EN 1992-1-1, devem ser cumpridas várias condições para uma armadura longitudinal resistente à torção:
- a armadura deve estar uniformemente distribuída ao longo do comprimento zi, mas em secções transversais pequenas a armadura pode estar concentrada nos cantos do estribo
- a distância axial máxima da armadura longitudinal é de 350 mm
A contribuição da armadura de pré-esforço não é considerada de acordo com a norma EN 1992-1-1.
A norma EN 1992-2 estabelece que a contribuição da armadura de pré-esforço pode ser considerada, mas o incremento máximo de tensão na armadura de pré-esforço não deve exceder Δσp ≤ 500MPa. Nesse caso, a fórmula pode ser modificada:
\[\frac{\sum{{{A}_{sl}}{{f}_{yd}}+\sum{{{A}_{p}}\Delta {{\sigma }_{p}}}}}{{{u}_{k}}}=\frac{{{T}_{ed}}}{2{{A}_{k}}}\cot \theta\]
No entanto, uma vez que o incremento da armadura de pré-esforço pode ser considerado, mas fica à escolha do utilizador. Atualmente, a armadura de pré-esforço não é considerada no cálculo.
O pressuposto do cálculo é que o aumento da deformação axial de cada armadura longitudinal resistente ao corte é constante (Δεs1,T = Δεs2,T = .... =Δεp1,T = Δεp2,T = ... = ΔεT = const.). A derivação é válida para um diagrama de trabalho de armadura bilinear com um ramo plástico horizontal. No caso de um diagrama com um ramo crescente, o cálculo deve ser modificado.
\[\frac{\sum\limits_{i=1}^{{{n}_{T}}}{{{A}_{sl,i,T}}\cdot \Delta {{\sigma }_{s,i,T}}}}{{{u}_{k}}}=\frac{{{T}_{ed}}}{2{{A}_{k}}}\cot \theta\]
\[\frac{\sum\limits_{i=1}^{{{n}_{T}}}{{{A}_{sl,i,T}}\cdot \Delta {{\varepsilon }_{T}}\cdot {{E}_{s,i,T}}}}{{{u}_{k}}}=\frac{{{T}_{ed}}}{2{{A}_{k}}}\cot \theta\]
\[\Delta {{\varepsilon }_{T}}=\frac{{{T}_{ed}}\cdot {{u}_{k}}}}{2{{A}_{k}}\cdot \sum\limits_{i=1}^{{n}_{T}}}{{{A}_{sl,i,T}}\cdot {{E}_{s,i,T}}}}\cot \theta\]
\[\frac{\sum\limits_{i=1}^{{{n}_{T}}}{{{A}_{sl,i,T}}\cdot \Delta {{\sigma }_{s,i,T}}}}{{{u}_{k}}}=\frac{{{T}_{ed}}}{2{{A}_{k}}}\cot \theta\]
\[\frac{\sum\limits_{i=1}^{{{n}_{T}}}{{{A}_{sl,i,T}}\cdot \Delta {{\varepsilon }_{T}}\cdot {{E}_{s,i,T}}}}{{{u}_{k}}}=\frac{{{T}_{ed}}}{2{{A}_{k}}}\cot \theta\]
\[\Delta {{\varepsilon }_{T}}=\frac{{{T}_{ed}}\cdot {{u}_{k}}}}{2{{A}_{k}}\cdot \sum\limits_{i=1}^{{n}_{T}}}{{{A}_{sl,i,T}}\cdot {{E}_{s,i,T}}}}\cot \theta\]
Ted. . . . o valor de projeto do binário aplicado na secção em consideração
θ . . . . . inclinação das diagonais de compressão em relação ao eixo longitudinal da viga (idêntica à da força de corte)
uk. . . . . perímetro da áreaAk
Af. . . . a área definida pela linha de centro da secção oca de substituição de paredes finas
ns,T. . . . número de armaduras longitudinais de betão que resistem ao binário
Asl,i,T. . . área da i-ésima armadura longitudinal de betão resistente ao binário
ΔεT. . . a alteração da transformação da armadura longitudinal de betão devido ao binário
Δσs,i,T. . alteração da tensão na i-ésima armadura longitudinal devido ao binário
Esl,i,T. . . módulo de elasticidade da i-ésima armadura longitudinal de betão que resiste ao binário
Incremento de tensão em cada armadura longitudinal devido ao binário aplicado:
\[\Delta {{\sigma }_{sl,i,T}}=\Delta {{\varepsilon }_{T}}\cdot {{E}_{sl,i,T}}\]