Base de conhecimento

Forças internas para secções 2D

Concrete

RCS

EN (Eurocode)

Beam

Este artigo também está disponível em:

A entrada de forças internas

A introdução de forças internas de elementos 2D depende do tipo de elemento 2D:

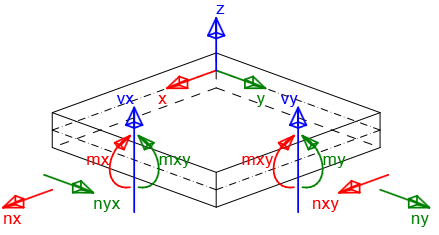
Laje - podem ser introduzidas forças de membrana (_nx, _ny e _nxy), momentos flectores (_mx,_my e _mxy) e forças de corte (_vx e _vy)
Casco-parede - podem ser introduzidas as forças de membrana (_nx, _ny e _nxy), os momentos flectores (_mx,_my e _mxy) e as forças de corte (_vx e _vy)
Laje - apenas podem ser introduzidos os momentos flectores (_mx,_my e _mxy) e as forças de corte (_vx e _vy)
Parede - apenas podem ser introduzidas as forças de membrana (_nx, _ny e _nxy)
Viga profunda - apenas podem ser introduzidas as forças de membrana (_nx, _ny e _nxy)

	Descrição
mx_(y)	Momento fletor na direção do eixo x (y). Um valor positivo provoca tensão na superfície inferior de um elemento 2D.
mxy_(yx)	Momento de torção em torno do eixo y (x) que actua na aresta paralela ao eixo x (y). O valor positivo provoca tensão de corte na superfície inferior de um elemento 2D. Como em cada ponto do teorema do elemento 2D a igualdade das tensões de corte horizontais é válida, os momentos de torção _mxy =_myx também são iguais em cada ponto do elemento 2D. Assim, apenas o valor de _mxyé introduzido no programa.
nx_(y)	Força normal na direção do eixo x (y). O valor positivo actua na direção do eixo x (y) e causa tensão na secção.
nxy_(yx)	Força normal que actua no plano central na direção do eixo y(x) na aresta paralela ao eixo x(y). O valor positivo actua na direção do eixo x(y)-. Como em cada ponto do elemento 2D o teorema da igualdade das tensões de corte horizontais é válido, as forças normais _nxy = _nyx também são iguais em cada ponto do elemento 2D. Assim, apenas o valor de _nxyé introduzido no programa.
vx_(y)	Força de corte que actua perpendicularmente ao plano central na aresta paralela ao eixo x(y). O valor positivo actua na direção do eixo z.

\[ \textsf{\textit{\footnotesize{Convenção de sinais de forças internas}}\]

Os seguintes tipos de combinações têm de ser definidos para verificações:

Estado limite último/acidental - os componentes de força interna definidos para este tipo de combinações são utilizados para verificações ULS de elementos 2D:

Capacidade N-M-M
Resposta N-M-M
Interação

e a verificação das disposições de pormenorização

Caraterística - os componentes de força interna definidos para este tipo de combinação são utilizados para a verificação da limitação de tensão (SLS)
Quase-permanente - os componentes da força interna definidos para este tipo de combinação são utilizados para a verificação da largura da fenda (SLS)

Observação:

Não é necessário introduzir as componentes de forças internas _vx e _vy para os tipos de combinação Caraterística e Quase-permanente, porque estes valores não são utilizados nas verificações.

Determinar a direção da verificação

A direção da verificação tem de ser determinada para a verificação correta do elemento 2D. A direção da verificação pode ser introduzida para cada tipo de combinação separadamente, utilizando os dois métodos seguintes:

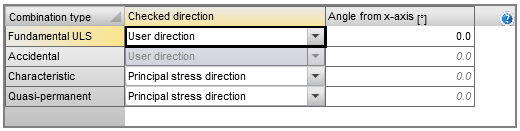
Direção definida pelo utilizador - o utilizador define a direção da verificação como um ângulo relativo ao eixo x no plano do elemento 2D. Esta opção é definida como predefinição para o tipo de combinação ULS e o valor predefinido do ângulo é 0 graus. As verificações são realizadas nas seguintes direcções:

Direção definida
Direção perpendicular à direção definida
Direção da diagonal de compressão na superfície superior
Direção da diagonal de compressão na superfície inferior

Direção das tensões principais - a direção de verificação é calculada automaticamente como a direção das tensões principais na superfície superior e inferior do elemento 2D. Esta opção é definida por defeito para os tipos de combinação Caraterística e Quase-permanente. As verificações são realizadas nas seguintes direcções:

Direção das tensões principais na superfície inferior
Direção perpendicular à direção das tensões principais na superfície inferior
Direção da diagonal de compressão na superfície inferior
Direção das tensões principais na superfície superior
Direção perpendicular à direção das tensões principais na superfície superior
Direção da diagonal de compressão na superfície superior

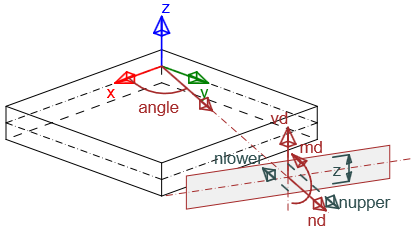
\[ \textsf{\textit{\footnotesize{Forças internas calculadas na direção de entrada pela teoria de Baumann}}}\]

Análise da direção de verificação para o estado limite último

Análise 1

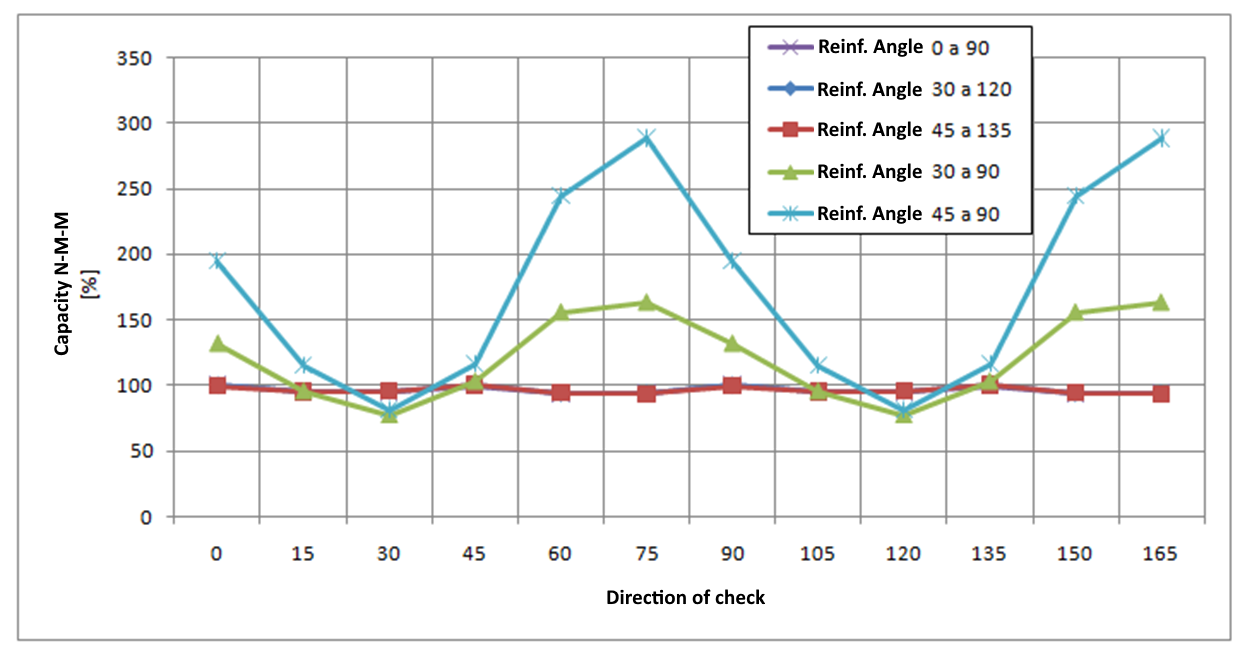
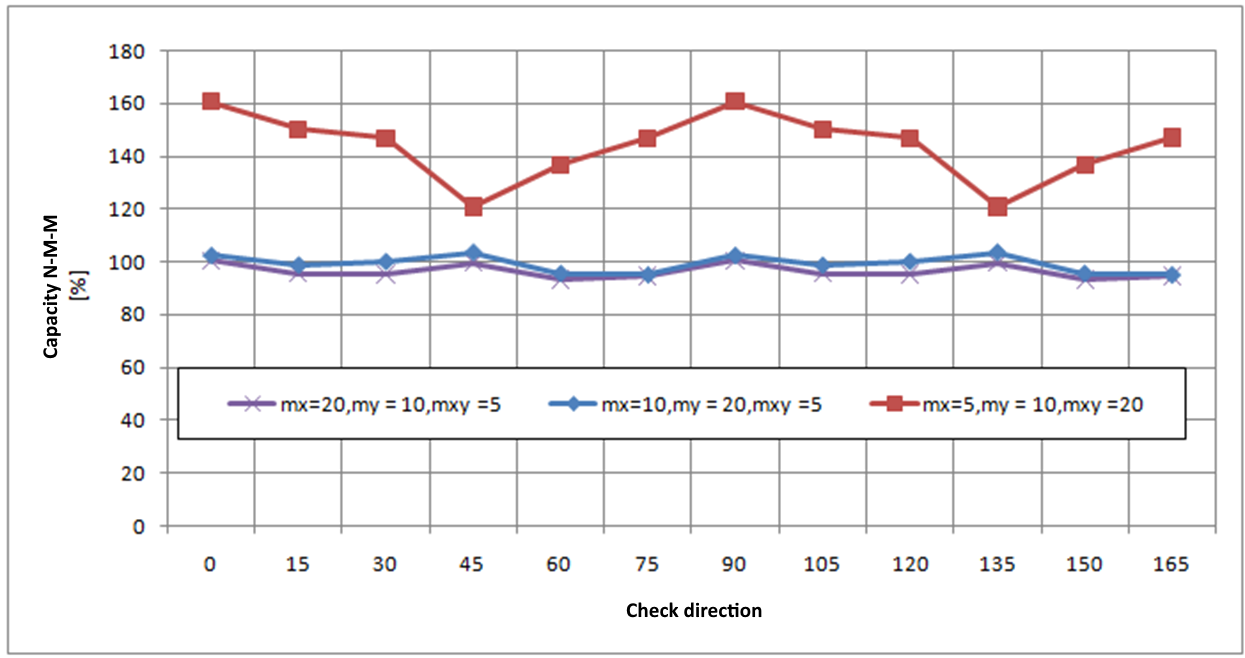
Para um elemento 2D carregado apenas por momentos flectores (_mx = 20 kNm/m,_my = 10 kNm/m, _mxy = 5 kNm/m ) com o ângulo da armadura e o ângulo da direção de verificação alterados para o estado limite último - os resultados são apresentados no gráfico seguinte:

A análise implica:

Se os varões de armadura forem perpendiculares entre si, os resultados da verificação são semelhantes para diferentes ângulos de direção de verificação, não dependem do ângulo de armadura definido e o valor máximo da verificação é encontrado para ângulos de 0, 45 e 90 graus. Assim, esta verificação pode ser realizada para uma direção predefinida de um ângulo de verificação de 0 graus.
Se as barras de armadura não forem perpendiculares entre si, os resultados das verificações diferem significativamente e o valor máximo da verificação é alcançado aproximadamente na direção correspondente à direção da armadura média. Assim, recomenda-se a alteração da direção de verificação predefinida ou a realização de verificações em mais direcções nos casos em que as barras de armadura não são perpendiculares entre si.

Análise 2

Para a armadura ortogonal, os valores dos momentos flectores e o ângulo foram alterados para a verificação do código ULS. Os resultados estão representados no gráfico:

A análise implica que, mesmo para diferentes valores de momentos flectores, o valor máximo da verificação do estado limite último é encontrado para as direcções de verificação 0, 45 e 90 graus. Assim, a verificação pode ser realizada para um ângulo de verificação predefinido de 0 graus. Uma conclusão semelhante é válida para elementos 2D carregados apenas por força normal ou carregados por força normal combinada com momentos flectores.

Novo cálculo de forças internas para direcções de verificação

As forças internas definidas são recalculadas para as direcções de verificação utilizando a fórmula de transformação de Baumann, descrita em Baumann, Th. : "Zur Frage der Netzbewehrung von Flächentragwerken". In: Der Bauingenieur 47 (1972), Berlim 1975. O procedimento de cálculo é o seguinte:

Cálculo das forças normais em ambas as superfícies do elemento 2D
Cálculo das forças principais em ambas as superfícies do elemento 2D
Cálculo das forças recalculadas para cada superfície em relação à direção de verificação definida
Cálculo das forças recalculadas para cada superfície até ao centro
Recálculo das forças de corte para a direção de verificação definida

Cálculo das forças normais em ambas as superfícies do elemento 2D

As forças internas definidas são recalculadas para ambas as superfícies utilizando as seguintes fórmulas:

\[{{n}_{x,low\left( upp \right)}}=\frac{{{n}_{x}}}{2}+\left( - \right)\frac{{{m}_{x}}}{z}\]

\[{{n}_{y,low\left( upp \right)}}=\frac{{{n}_{y}}}{2}+\left( - \right)\frac{{{m}_{y}}}{z}\]

\[~~~~~{{n}_{xy,low\left( upp \right)}}=\frac{{{n}_{xy}}}{2}+\left( - \right)\frac{{{m}_{xy}}}{z}\]

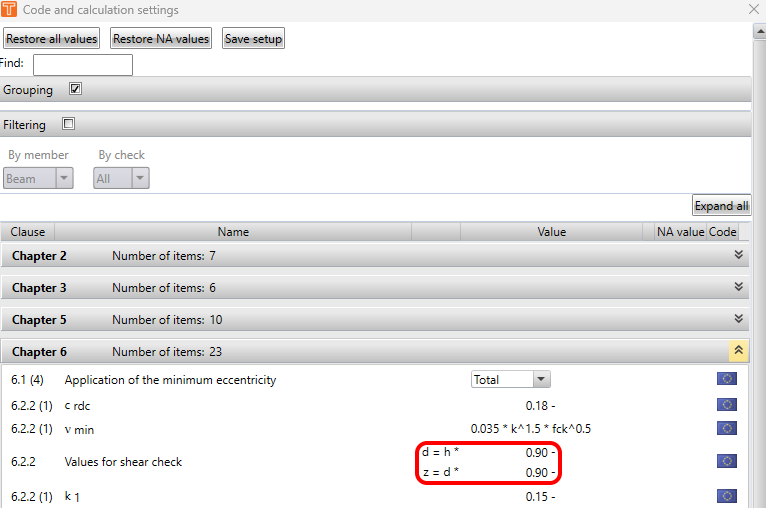
O braço de alavanca das forças internas (z) tem de ser determinado para o novo cálculo das forças internas. O braço de alavanca das forças internas é determinado a partir do método da deformação limite no carregamento pelo momento fletor principal nas direções dos momentos principais _m1 em ambas as superfícies. Se os momentos principais forem iguais a zero ou se o equilíbrio não for encontrado na direção dos momentos principais, o braço de alavanca das forças internas é determinado de acordo com a fórmula:

\[z=x\cdot d\]

	Descrição
x	O coeficiente para o cálculo do braço das forças internas é definido na configuração do código nacional.
d	A altura efectiva da secção transversal calculada separadamente para as superfícies superior e inferior do elemento 2D. Para a superfície inferior, é a distância entre o centróide dos varões de armadura na superfície inferior e a borda superior da secção transversal. Para a superfície superior, é a distância do centróide dos varões de armadura na superfície superior até à borda inferior da secção transversal.

Observação:

O braço das forças internas pode ser verificado na verificação da resposta N-M-M. Apenas os momentos de flexão têm de ser introduzidos e a direção de verificação tem de corresponder à direção do momento principal.

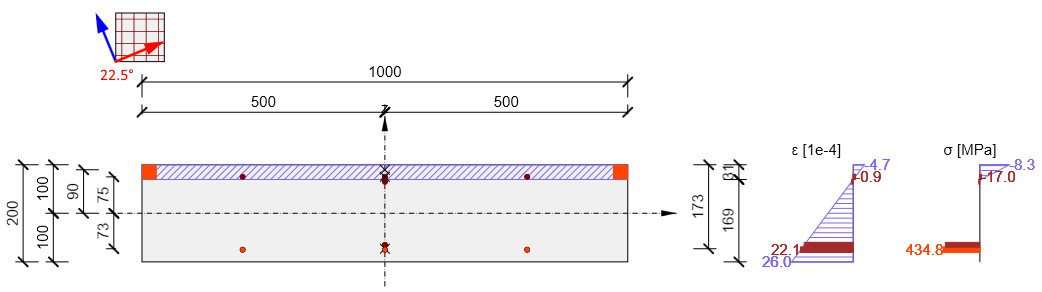
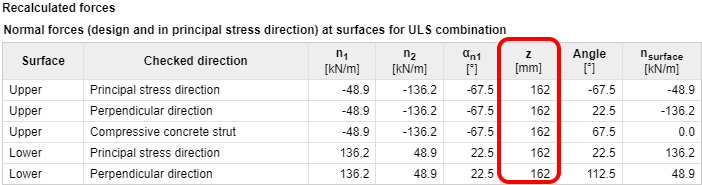
No diagrama seguinte, é apresentada uma verificação do braço de alavanca dos esforços internos para momentos flectores _mx = 20 kNm/m,_my = 10 kNm/m, _mxy = 5 kNm/m. A direção dos momentos principais foi calculada como _αm1 = 22,5 graus e a resposta da secção transversal foi calculada para determinar o braço de alavanca das forças internas.

Observação:

Os braços de alavanca das forças internas para o recálculo das forças internas na direção da verificação e os braços de alavanca das forças internas para as verificações podem ser diferentes, porque o braço de alavanca das forças internas para o recálculo é determinado numa secção carregada por momentos principais na direção dos momentos principais, e o braço de alavanca das forças internas para a verificação é determinado numa secção carregada por momentos flectores e forças normais na direção da verificação. Os valores dos braços de alavanca de força interna para todos os tipos de combinação são apresentados na tabela Forças recalculadas no navegador Forças internas na secção.

Cálculo de forças internas em ambas as superfícies

As forças principais em ambas as superfícies do elemento 2D são calculadas utilizando a fórmula:

\[{{n}_{1,bot\left( top \right)}}=\frac{{{n}_{x,low\left( upp \right)+}}{{n}_{y,low\left( upp \right)}}}{2}+\frac{1}{2}\sqrt{{{\left( {{n}_{x,low\left( upp \right)-}}{{n}_{y,low\left( upp \right)}} \right)}^{2}}+4\cdot {{n}_{xy,low\left( upp \right)}}\]

\[{{n}_{2,bot\left( top \right)}}=\frac{{{n}_{x,low\left( upp \right)+}}{{{n}_{y,low\left( upp \right)}}}{2}-\frac{1}{2}\sqrt{{{\left( {{n}_{x,low\left( upp \right)-}}{{{n}_{y,low\left( upp \right)}} \right)}^{2}}+4\cdot {{n}_{xy,low\left( upp \right)}}\]

E a direção das forças principais é calculada utilizando a fórmula:

\[{{\alpha }_{n1,low\left( upp \right)}}=0,5\cdot {{\tan }^{-1}}\left( \frac{2\cdot {{n}_{xy,low\left( upp \right)}}}{{{n}_{x,low\left( upp \right)}}-{{n}_{y,low\left( upp \right)}} \right)\]

Observação:

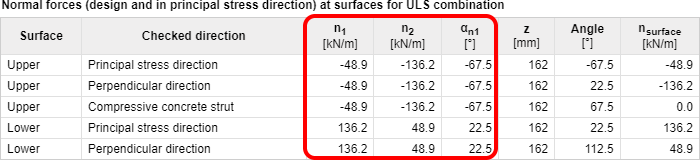
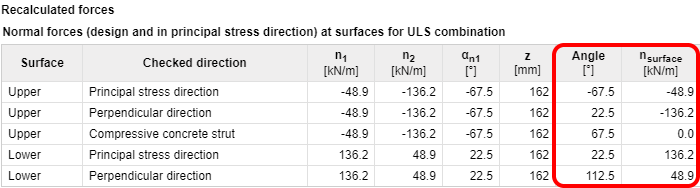
As forças principais e a direção das forças principais para ambas as superfícies do elemento 2D são apresentadas para todos os tipos de combinação na tabela Forças recalculadas no navegador Forças internas na secção.

Cálculo de forças internas recalculadas em superfícies para a direção de verificação definida

O recálculo das forças principais para as direcções de verificação é realizado separadamente para cada superfície utilizando a fórmula de transformação de Baumann:

\[{{n}_{superfície,i,low\left( upp \right)}}=\frac{{{n}_{1,low\left( upp \right)}}\cdot \sin \left( {{\alpha }_{j,low\left( upp \right)}} \right)\cdot \sin \left( {{\alpha }_{k,low\left( upp \right)}} \right)+{{{n}_{2,low\left( upp \right)}}\cdot \cos \left( {{\alpha }_{j,low\left( upp \right)}} \right)\cdot \cos \left( {{\alpha }_{k,low\left( upp \right)}} \right)}{\sin \left( {{\alpha }_{j,low\left( upp \right)}}-{{\alpha }_{i,low\left( upp \right)}} \right)\cdot \sin \left( {{\alpha }_{k,low\left( upp \right)}}-{{\alpha }_{i,low\left( upp \right)}} \right)}\]

	Descrição
i, j, k, i	Índice da direção de verificação (direção de recálculo das forças internas) i, j, k, i = 1, 2, 3, 1 . E. G. Para a superfície inferior e cálculo da força na direção j (ângulo _α2), a fórmula é \[{{n}_{superfície,2,baixo}}=\frac{{{n}_{1,baixo}}\cdot \sin {{\alpha }_{3,baixo}}\cdot \sin {{\alpha }_{1,baixo}}+{{n}_{2,baixo}}\cdot \cos {{\alpha }_{3,baixo}\cdot \cos {{\alpha }_{1,low}}}{\sin \left( {{\alpha }_{3,low}}-{{\alpha }_{2,low}} \right)\cdot \sin \left( {{\alpha }_{1,low}}-{{\alpha }_{2,low}} \right)}\]
\[{{\alpha }_{i,j,k,low\left( upp \right)}}\]	O ângulo entre a direção de verificação definida ou a direção do suporte de compressão e a direção das forças principais na superfície inferior ou superior do elemento 2D. Direção de verificação definida α1_{, low(upp)} = _α1 - α_low(upp) Dir. perpendicular à direção definida α2_{, baixo(upp)} = _α2 - α_baixo(upp) A direção de verificação da escora de compressão α3_{, baixa(upp)} = _α3 - α_baixa(upp)
_α1	Direção de verificação definida para a combinação específica
_α2	A direção perpendicular à direção definida, α2_{= α1} + 90 graus
_α3	Verifique a direção na direção da escora de compressão no plano do elemento 2D. Esta direção é optimizada para minimizar a força nesta direção.

Observação:

Se a direção de verificação for idêntica à direção das tensões principais, as forças na escora de compressão são zero, pelo que esta direção é negligenciada na verificação

A direção da escora de compressão para todos os estados de tensão exceto o estado hiperbólico de tensão (n1_,low(upp) > 0 e n1_,low(upp) < 0) pode ser calculada de acordo com a fórmula:

_α3 = 0,5(_α1 + _α2)

As forças internas recalculadas para ambas as superfícies do elemento 2D e todas as direcções de verificação, incluindo a direção da escora de compressão, são apresentadas na tabela Forças recalculadas

Transformação das forças internas recalculadas para o centroide da secção

Para a verificação do elemento 2D, as forças de superfície numa determinada direção têm de ser recalculadas para o centro de gravidade da secção. O resultado é a força normal nd_,i e o momento fletor md_,I atuando no centroide da secção do elemento 2D.

md_,i = nlower_,i-zs,low+ nupper_,i-zs,upp

_{nd ,i} = nlower_,i + nupper_,i

	Descrição
nlower_,i	Forças superficiais recalculadas na superfície inferior na ^i-ésima direção de verificação, quando nlower_,i = nsurface_,low,i.
nupper_,i	Forças internas recalculadas na superfície superior na ^i-ésima direção de verificação, quando nupper_,i = nsurface_,upp,i.
zs_{,low (upp)}	Distância do centro de gravidade do betão comprimido ou do centro de gravidade da armadura à superfície inferior (superior), quando z = zs_,low+ zs_,upp

Observação:

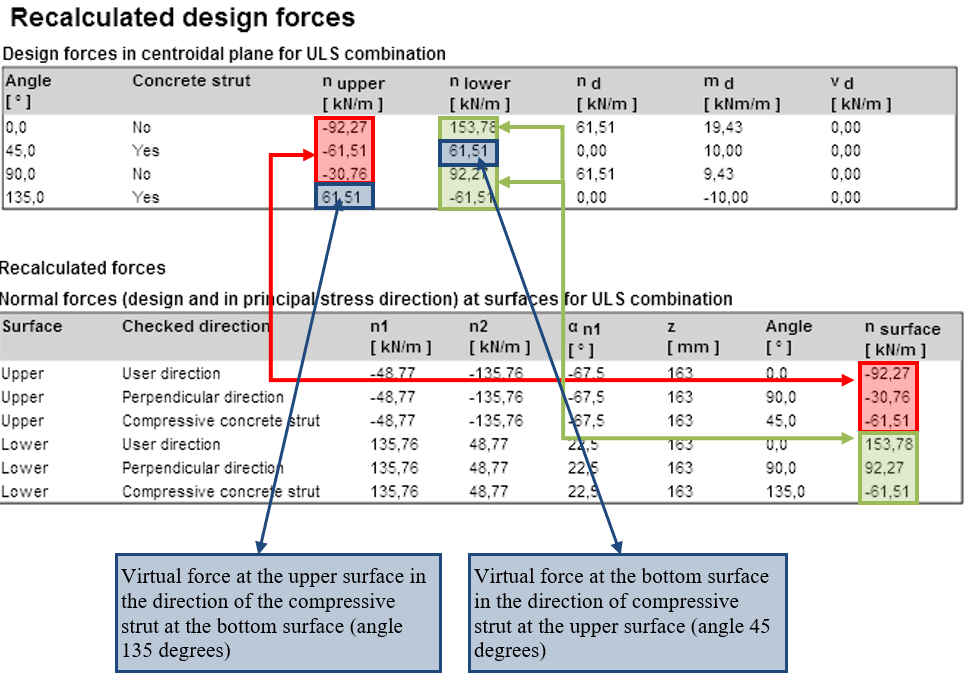
Se as direcções das escoras de compressão na superfície inferior e superior forem diferentes, para o novo cálculo das forças para o centróide é necessário calcular as forças virtuais na superfície inferior na direção da escora de compressão na superfície superior e vice-versa.

\[ \textsf{\textit{\footnotesize{Forças de dimensionamento recalculadas}}}\]

Recálculo das forças de corte para a direção de verificação definida

As forças de corte são recalculadas para a direção da verificação utilizando a fórmula:

\[{{v}_{d,i}}={{v}_{x}}\cdot \cos ({{\alpha }_{i}})+{{v}_{y}}\cdot \sin ({{\alpha }_{i}})\]

e a força de cisalhamento máxima é:

\[{{v}_{d,max~}}=\sqrt{{{v}_{x}}^{2}+{{v}_{y}}^{2}}\]

e actua na direção

\[\beta ={{\tan }^{-1}}\left( \frac{{{v}_{y}}}{{{v}_{x}}} \right)\]

	Descrição
_αi	Verificar o ângulo na ^i-ésima direção

Observação:

Ao verificar um elemento 2D com forças de corte relativamente grandes, é adequado verificar o elemento 2D na direção da força de corte máxima, o que significa que a verificação da direção definida corresponde ao ângulo β

Comparação do recálculo de forças internas utilizando vários métodos

Recálculo das forças de acordo com a norma EN 1992-1-1

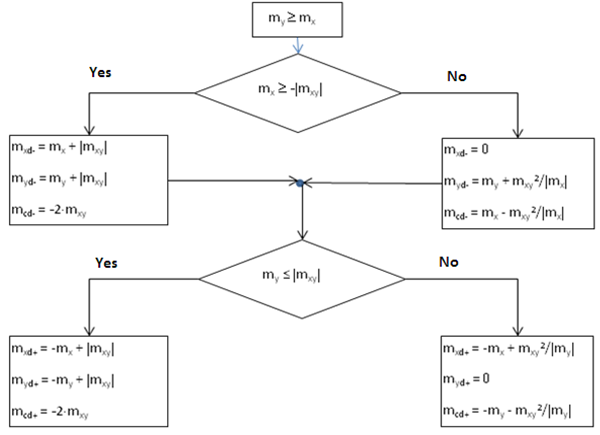
O método descrito na norma EN 1992-1-1 é utilizado em vários programas e na prática para calcular os esforços internos de cálculo. A norma EN 1992-1-1 tem em conta apenas as direcções perpendiculares da armadura. O cálculo das forças de dimensionamento com a influência do momento de torção é descrito no seguinte fluxograma, onde_my³mx. Um diagrama semelhante pode ser criado para momentos_my < _mx

	Descrição
mxd+_{, mxd-}	Dimensionamento do momento fletor na direção do eixo x para dimensionamento e verificação da armadura na superfície inferior (-) ou superior (+)
_myd+ _myd-	Dimensionamento do momento fletor na direção do eixo y para dimensionamento e verificação da armadura na superfície inferior (-) ou superior (+)
mcd+_{, mcd-}	Dimensionamento do momento fletor na escora de betão de compressão na superfície inferior (-) ou superior (+), que tem de ser suportado pelo betão

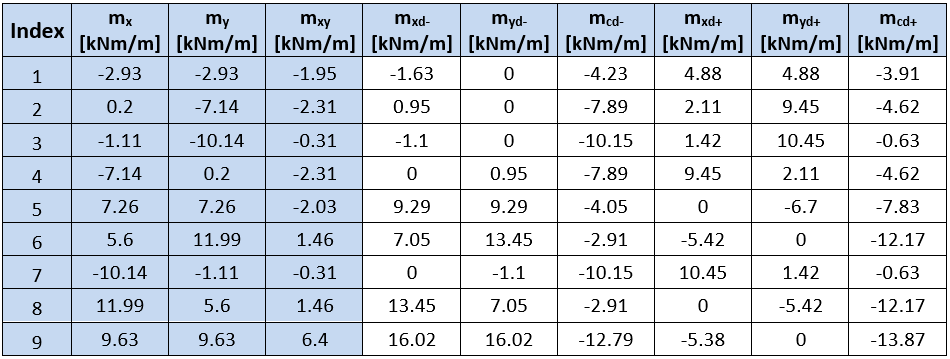
Os valores das forças de dimensionamento recalculadas para o tipo de barra = Laje, calculados utilizando o método descrito em EN, são apresentados na tabela seguinte:

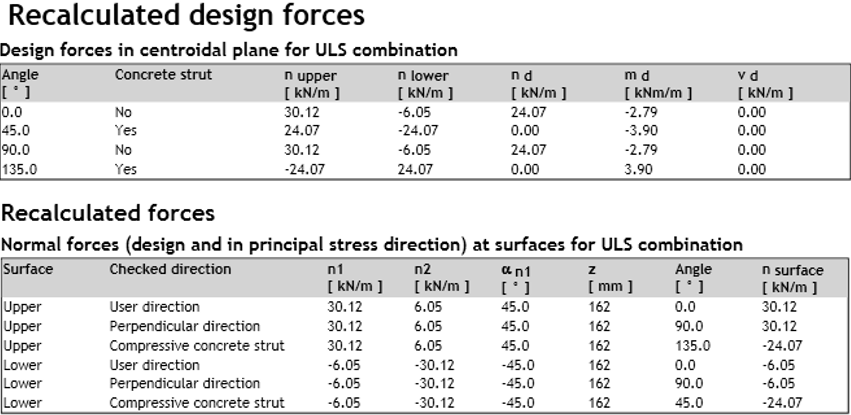
No IDEA StatiCa RCS, os valores dos momentos na superfície superior e inferior não são apresentados, mas sim os valores das forças normais em ambas as superfícies e os valores dos momentos recalculados para o centro de gravidade da secção transversal.

Os momentos nas superfícies inferior e superior podem ser calculados utilizando forças de superfície, que são apresentadas na saída numérica, utilizando a fórmula:

\[{{m}_{superfície,i,dlow\left( upp \right)}}={{n}_{superfície,i,low\left( upp \right)}}\cdot z\]

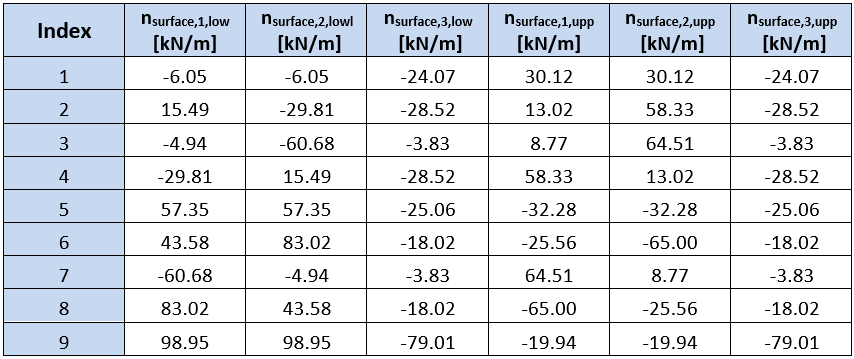
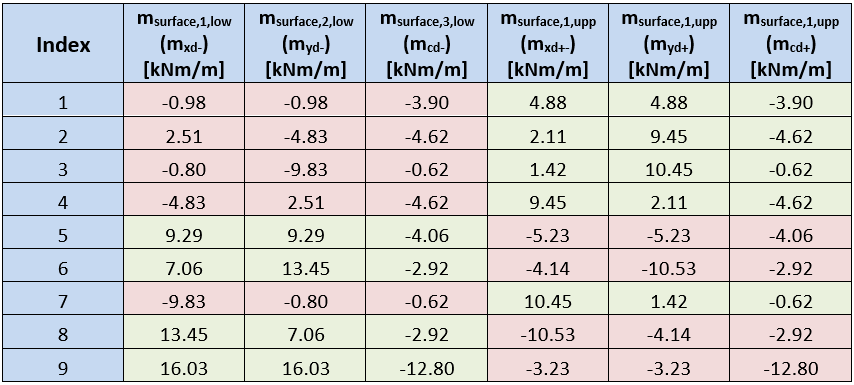
Os valores das forças de superfície e dos momentos recalculados são apresentados nas tabelas seguintes:

As tabelas mostram que os momentos nas superfícies da laje calculados no IDEA Concrete e calculados de acordo com o método descrito na EN, correspondem apenas numa superfície. Esta diferença é causada pela otimização diferente da escora de betão. O método utilizado no IDEA StatiCa RCS procura o ângulo da escora de compressão com a força mínima na escora. O método descrito em EN procura uma soma mínima de forças negativas de todas as direcções.

Comparação do cálculo de forças internas com os programas RFEM e SCIA Engineer

Para comparar os resultados dos esforços internos recalculados nos programas IDEA Concrete, RFEM e SCIA Engineer (SEN), foi preparado um modelo simples de laje com dimensões de 6 m x 4 m e espessura de 200 mm. A laje é apoiada com linhas de apoio nas extremidades e carregada com uma carga uniforme de 10 ^kN/m2.

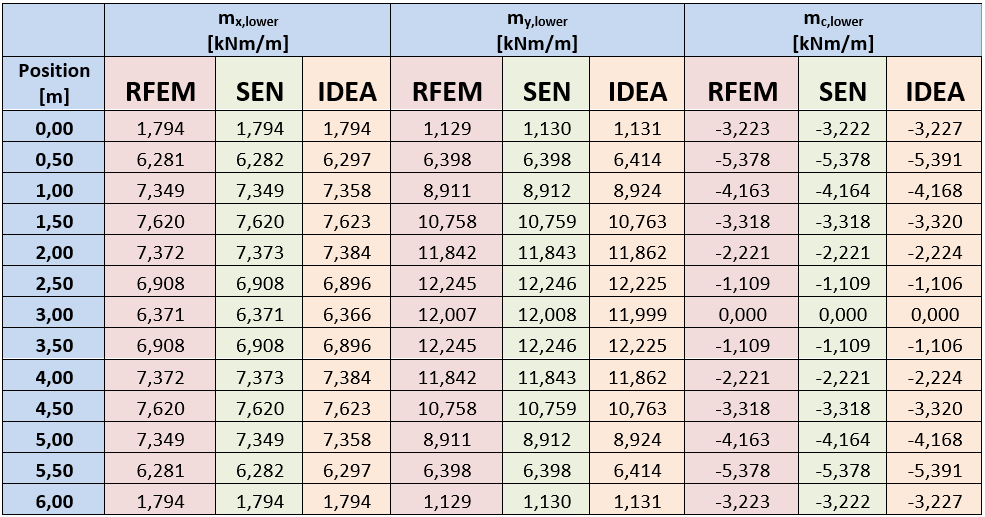
Para simplificar a apresentação, apenas são apresentados os valores das forças internas recalculadas numa secção longitudinal. A distância da secção à borda da laje é de 1,5 m. Os esforços internos calculados no programa RFEM foram utilizados como valores de entrada para o IDEA Concrete.