Connection to unstiffened flanges
Description
In this chapter, component-based finite element method (CBFEM) of a fillet weld connecting a plate to an unstiffened column is verified on component method (CM). The steel plate is connected to the open and box section columns and loaded in tension.
Analytical model
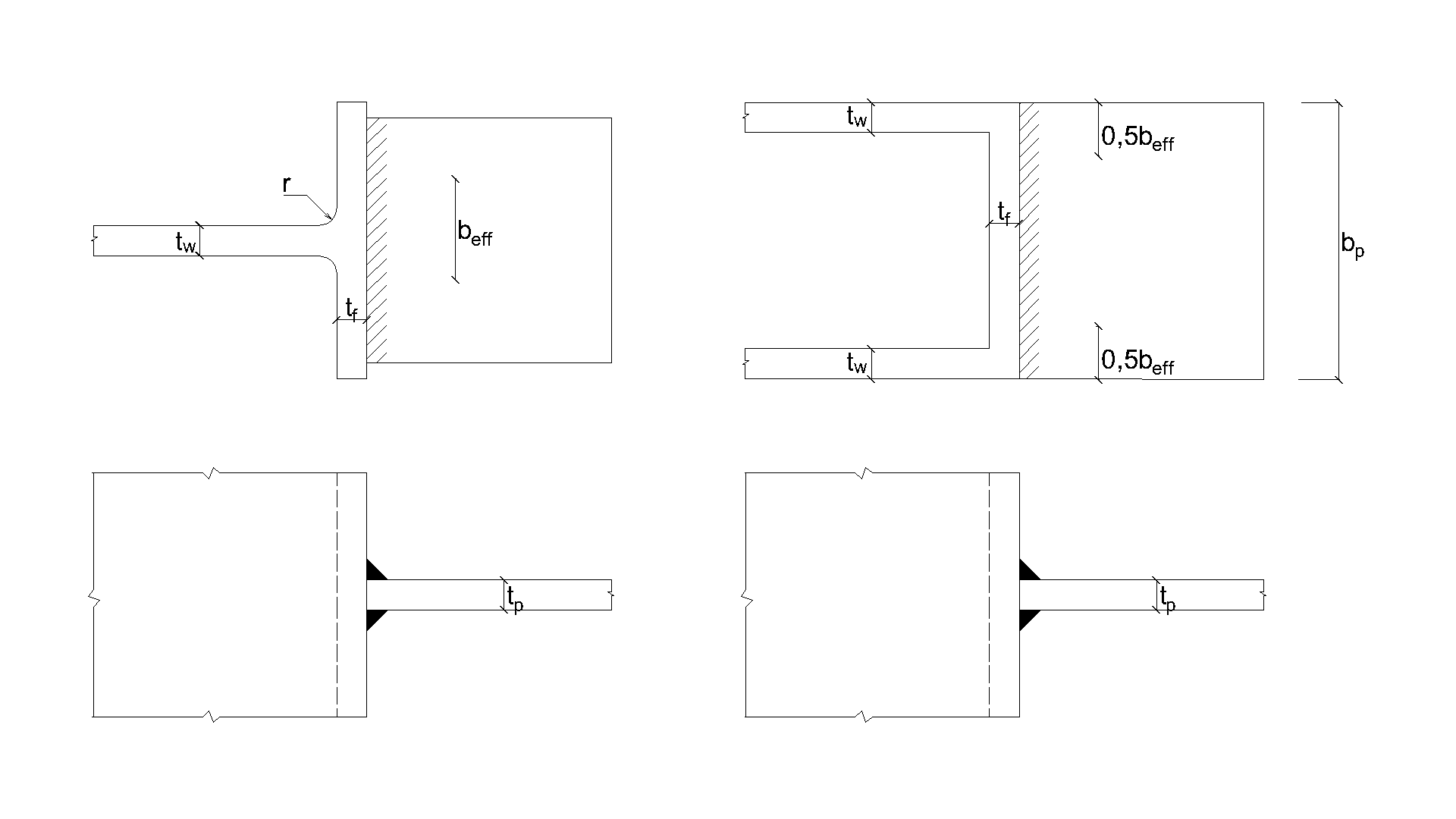
The fillet weld is the only component examined in the study. The welds are designed according to Chapter 4 in EN 1993-1-8:2005 to be the weakest component in the joint. The design resistance of the fillet weld is described in Section 4.1. The force applied perpendicular to a flexible plate, which is welded to an unstiffened section, is limited. The stresses are concentrated in an effective width while the weld resistance around the unstiffened parts is neglected, as shown in Fig. 4.5.1. For an unstiffened I or H section the effective width is obtained according to:
\[ b_\mathrm{eff} = t_\mathrm{w} + 2s + 7kt_\mathrm{f} \qquad (4.5.1)\]
\[ k = \frac{t_\mathrm{f} \cdot f_\mathrm{y,f} }{ t_\mathrm{p} \cdot f_\mathrm{y,p}} \qquad (4.5.2)\]
The dimension s is for a rolled section \(s =r\) and for a welded section \(s = \sqrt{2} \cdot a \) . For a box or channel section, the effective width should be obtained from:
\[ b_\mathrm{eff} = 2t_\mathrm{w} + 5 t_\mathrm{f} \quad \textrm{but}\quad b_\mathrm{eff} \leq 2t_\mathrm{w} + 5 kt_\mathrm{f}\qquad (4.5.1)\]
\[\sqrt{ \sigma_{\perp}^2 + 3 \cdot \left( \tau_{\perp}^2 + \tau_{\parallel}^2\right)} \leq \frac{f_u}{\beta_{\mathrm{w}} \cdot \gamma_{\mathrm{M2}}}\]
\[\sigma_{\perp} = \tau_{\perp} = \frac{\sigma_{N}}{\sqrt{2}} = \frac{N}{b_\mathrm{eff} \cdot a}\cdot \frac{1}{\sqrt{2}} \]
\[ \tau_{\parallel} = 0\]
\[ \sqrt{ \left( \frac{\sigma_{N}}{\sqrt{2}} \right)^2 + 3 \cdot \left( \frac{\sigma_{N}}{\sqrt{2}} \right)^2} \leq \frac{f_u}{\beta_{\mathrm{w}} \cdot \gamma_{\mathrm{M2}}}\]
\[ \sqrt{ \left( \frac{N}{b_\mathrm{eff} \cdot a}\cdot \frac{1}{\sqrt{2}} \right)^2 + 3 \cdot \left( \frac{N}{b_\mathrm{eff}\cdot a}\cdot \frac{1}{\sqrt{2}} \right)^2} \leq \frac{f_u}{\beta_{\mathrm{w}} \cdot \gamma_{\mathrm{M2}}}\]
\[ N \leq \frac{f_{u} \cdot b_\mathrm{eff} \cdot a }{\beta_{\mathrm{w}} \cdot \gamma_{\mathrm{M2}} \cdot \sqrt{2}} \]
Where:
\(a\) - weld throat thickness
\(N\) - normal force acting on beam
\(b_\mathrm{eff}\) - total effective welds length
\(\beta_{\mathrm{w}}\) - correlation factor taken from EN 1993-1-8 Table 4.1
\(f_u\) - nominal ultimate tensile strength of the weaker part joined
\(\gamma_{\mathrm{M2}}\) - partial safety factor for welds
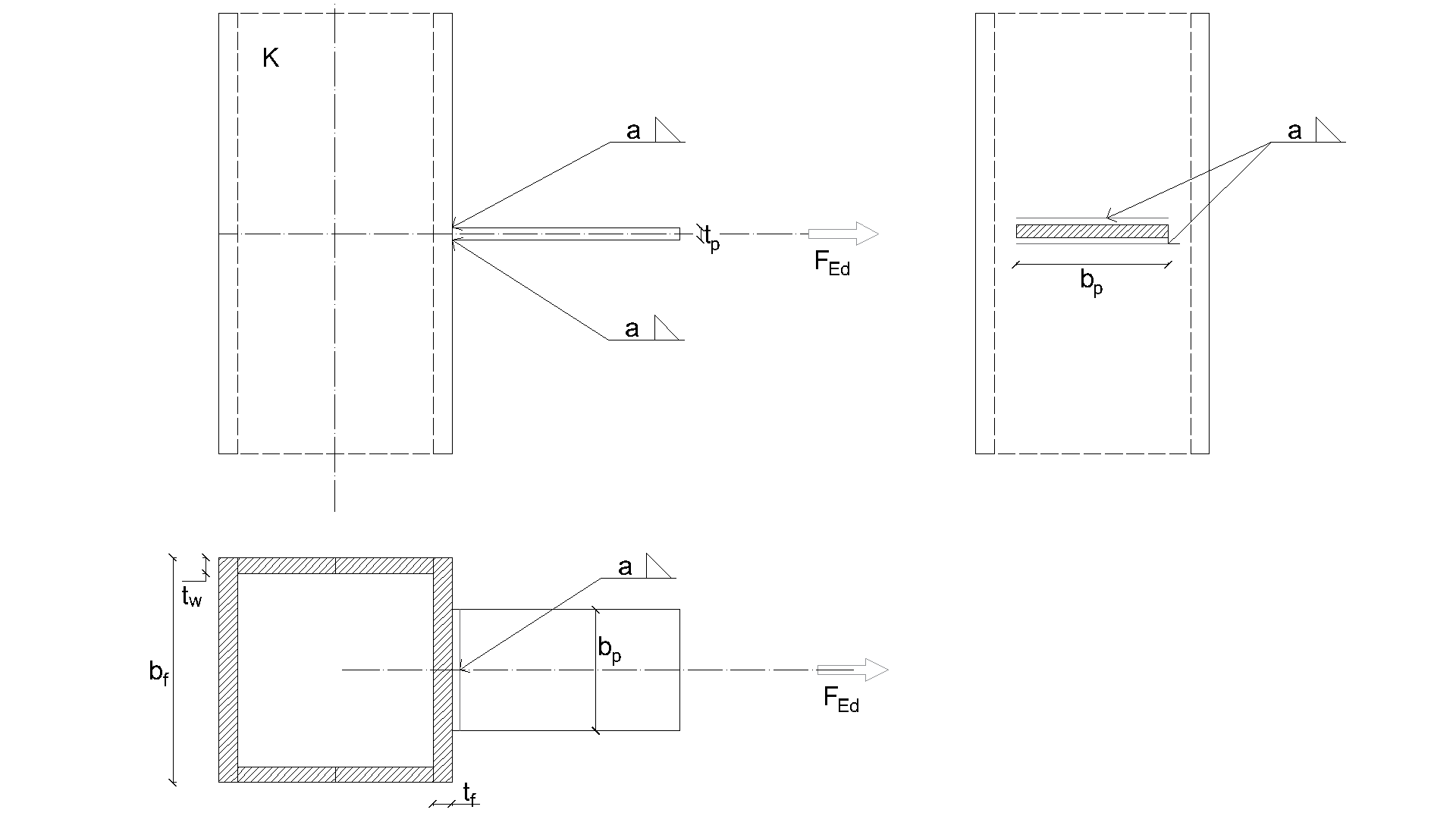
\[ \textsf{\textit{\footnotesize{Fig. 4.5.1 Effective width of an unstiffened joint (Fig. 4.8 in EN 1993-1-8:2005)}}}\]
Numerical model
The weld component in CBFEM is described in General theoretical background and EN theoretical background. The plastic branch is reached in a part of the weld, and stress peaks are redistributed along the weld length.
Verification of resistance
Design resistance calculated by CBFEM is compared with the results of CM. The weld design resistance is compared only. Overview of considered examples and material is given in Tab. 4.5.1. Geometry of joints with dimensions is shown in Fig. 4.5.2.
\[ \textsf{\textit{\footnotesize{Tab. 4.5.1 Examples overview}}}\]
\[ \textsf{\textit{\footnotesize{a) Flexible plate to open section b) Flexible plate to box section}}}\]
\[ \textsf{\textit{\footnotesize{Fig. 4.5.2 Joint geometry and dimentions}}}\]
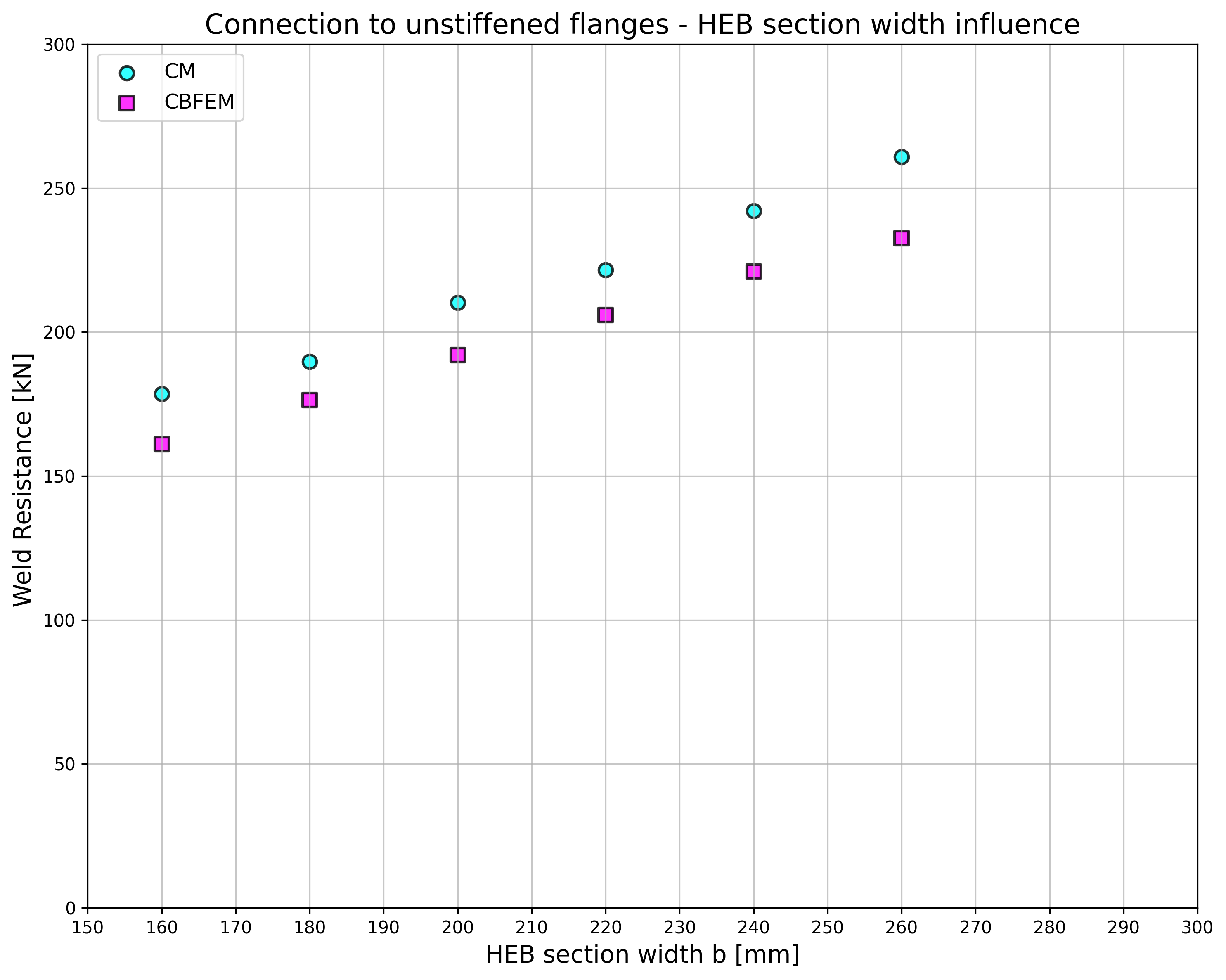
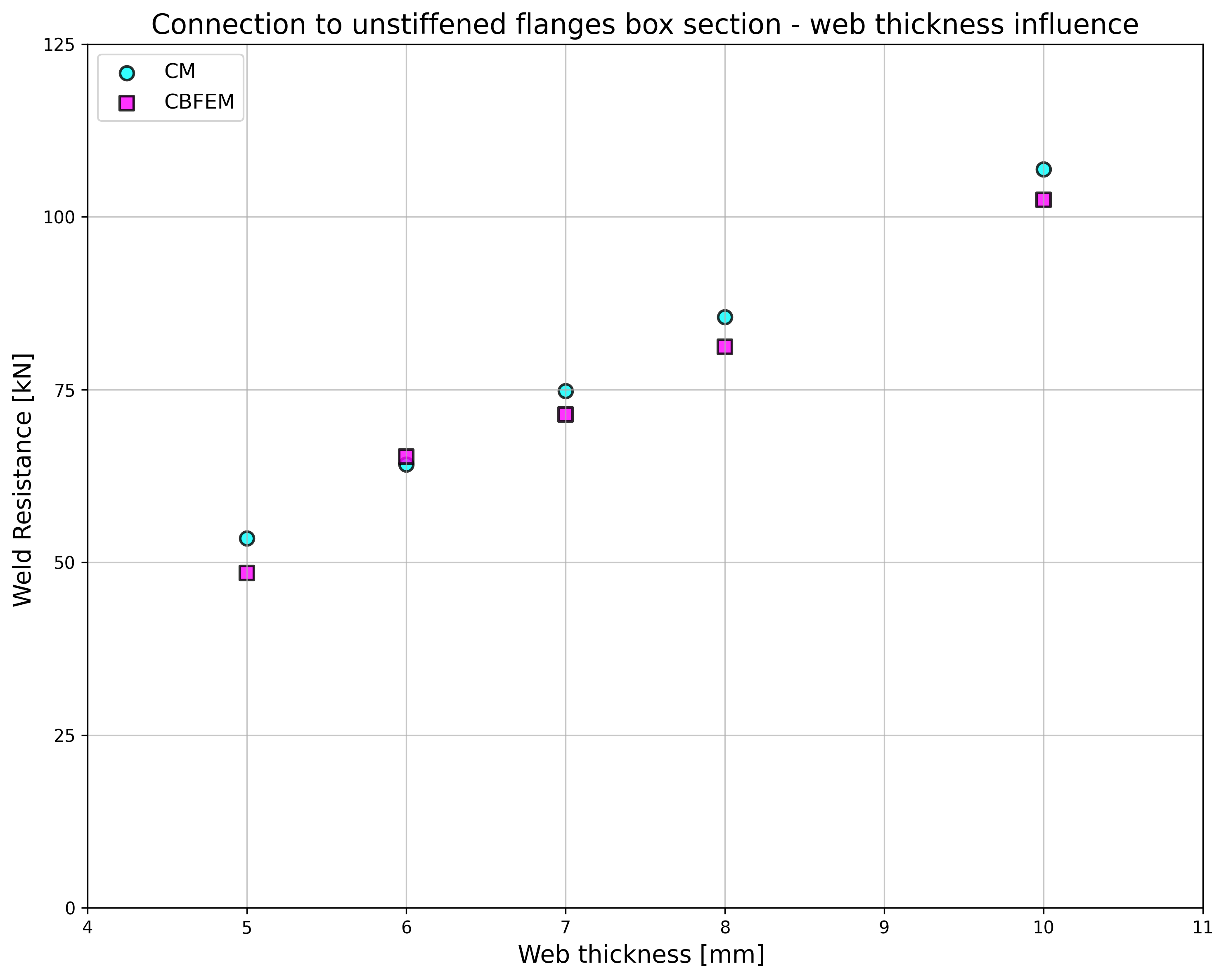
The results are presented in Tab. 4.5.2. The study is performed for two parameters: flange width of the HEB section and web thickness of the box section. The flexible plate is loaded in tension. The influence of the flange width of HEB section on design resistance of a joint is shown in Fig. 4.5.3. The relation between the web thickness of box section on design resistance of a joint is shown in Fig. 4.5.4.
\[ \textsf{\textit{\footnotesize{Tab. 4.5.2 Comparison of CBFEM and CM}}}\]
Results of CBFEM and CM are compared in a sensitivity study. The influence of the flange width of HEB section on design resistance of a joint is studied in Fig. 4.5.3. The influence of the web thickness of box section on design resistance of a joint is presented in Fig. 4.5.4. The parametric studies show very good agreement of the results for all weld configurations.
\[ \textsf{\textit{\footnotesize{Fig. 4.5.3 Flange width of the HEB section Fig. 4.5.4 Web thickness of the box section}}}\]
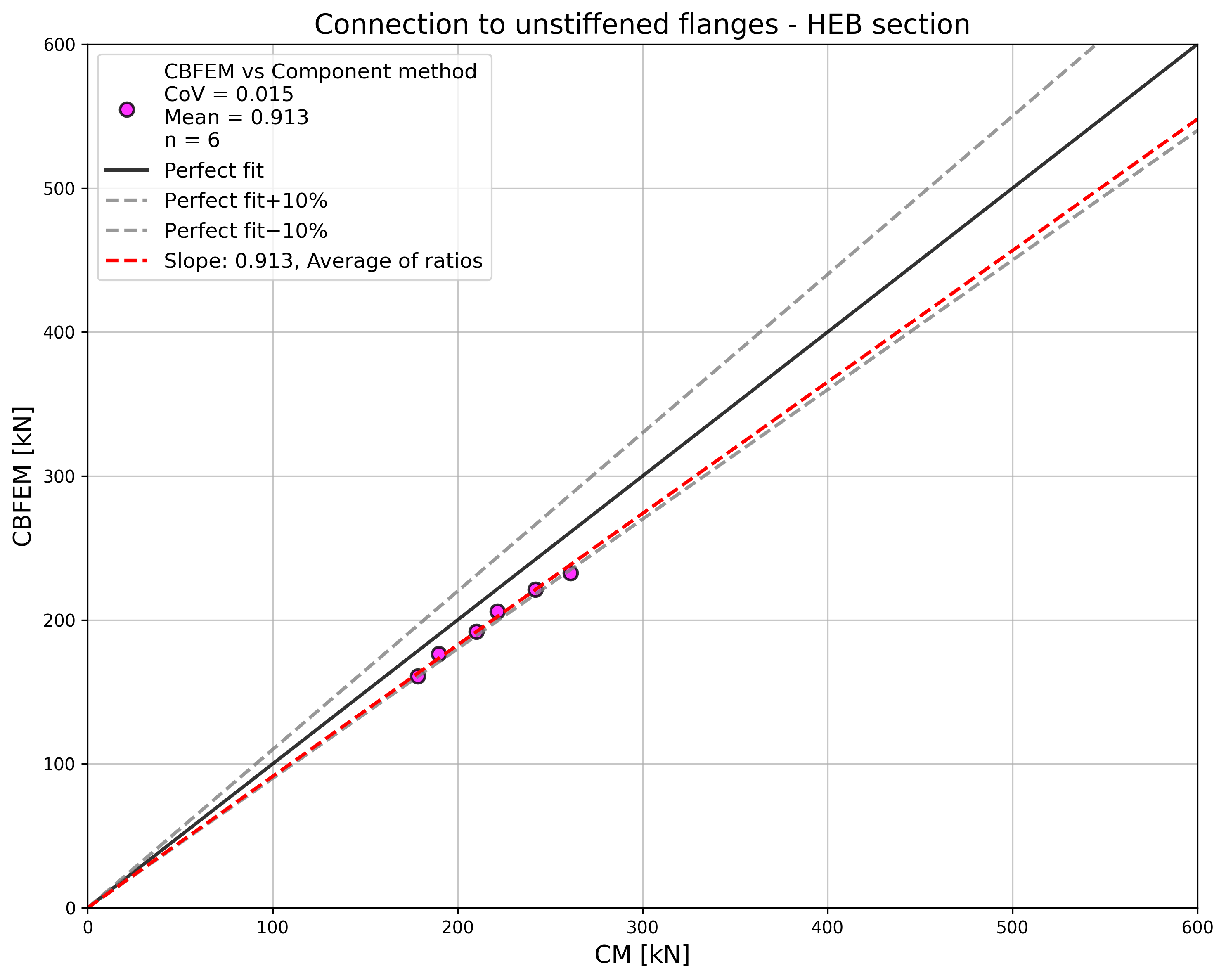
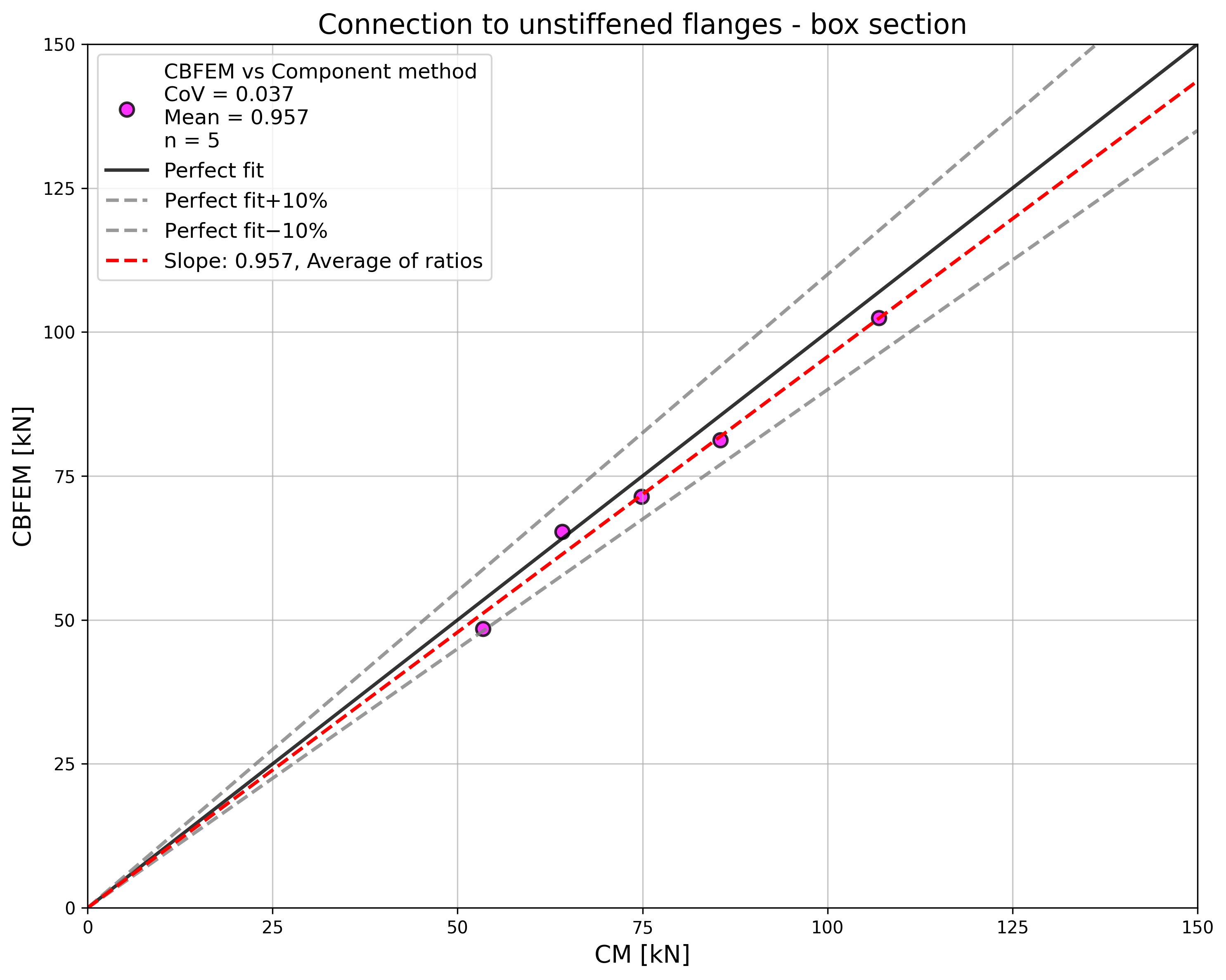
The results of the sensitivity study are summarized in a diagram comparing design resistances of CBFEM and CM; see Fig. 4.5.5 illustrating the accuracy of the CBFEM model.
\[ \textsf{\textit{\footnotesize{Fig. 4.5.5 Verification of CBFEM to CM}}}\]
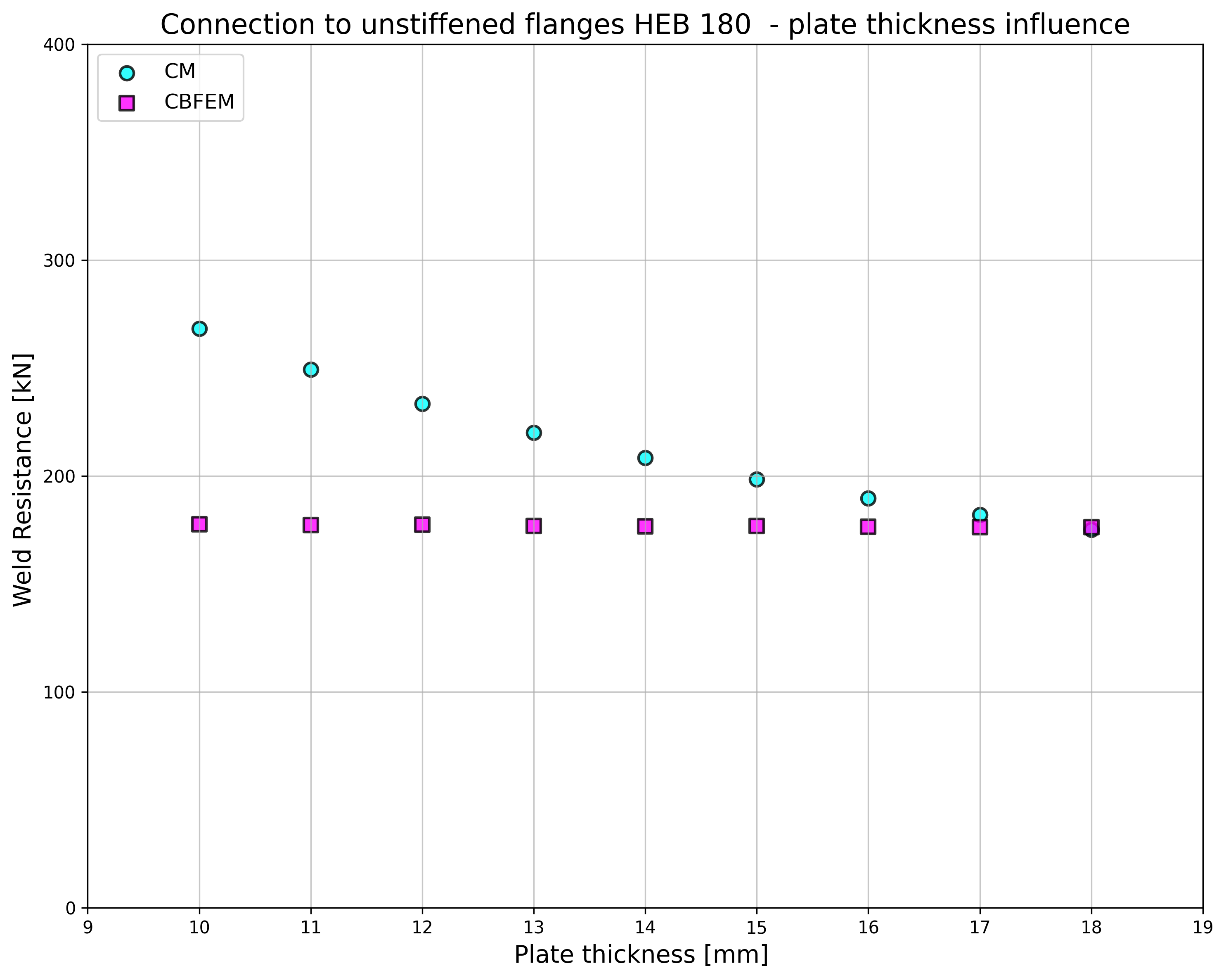
The influence of the plate thickness on the design resistance of the weld is shown in Fig. 4.5.6. The column cross-section is HEB 180 with a flange thickness of 14 mm. A weld connecting a plate thicker than the column flange has the same resistance for CM and CBFEM. On the other hand, the weld connecting the plate to column flange of the same or smaller thickness has in numerical models design resistance smaller by 20%. The plate thickness is not taken into account in numerical models with shell elements, which causes the difference.
\[ \textsf{\textit{\footnotesize{Fig. 4.5.6 Influence of plate thickness on the resistance of joint with unstiffened column HEB180}}}\]
Benchmark example
Inputs
Column
• Steel S235
• RHS 200/200/5
Flexible plate
• Steel S235
• Thickness tp = 17 mm
• Width bp = 190 mm
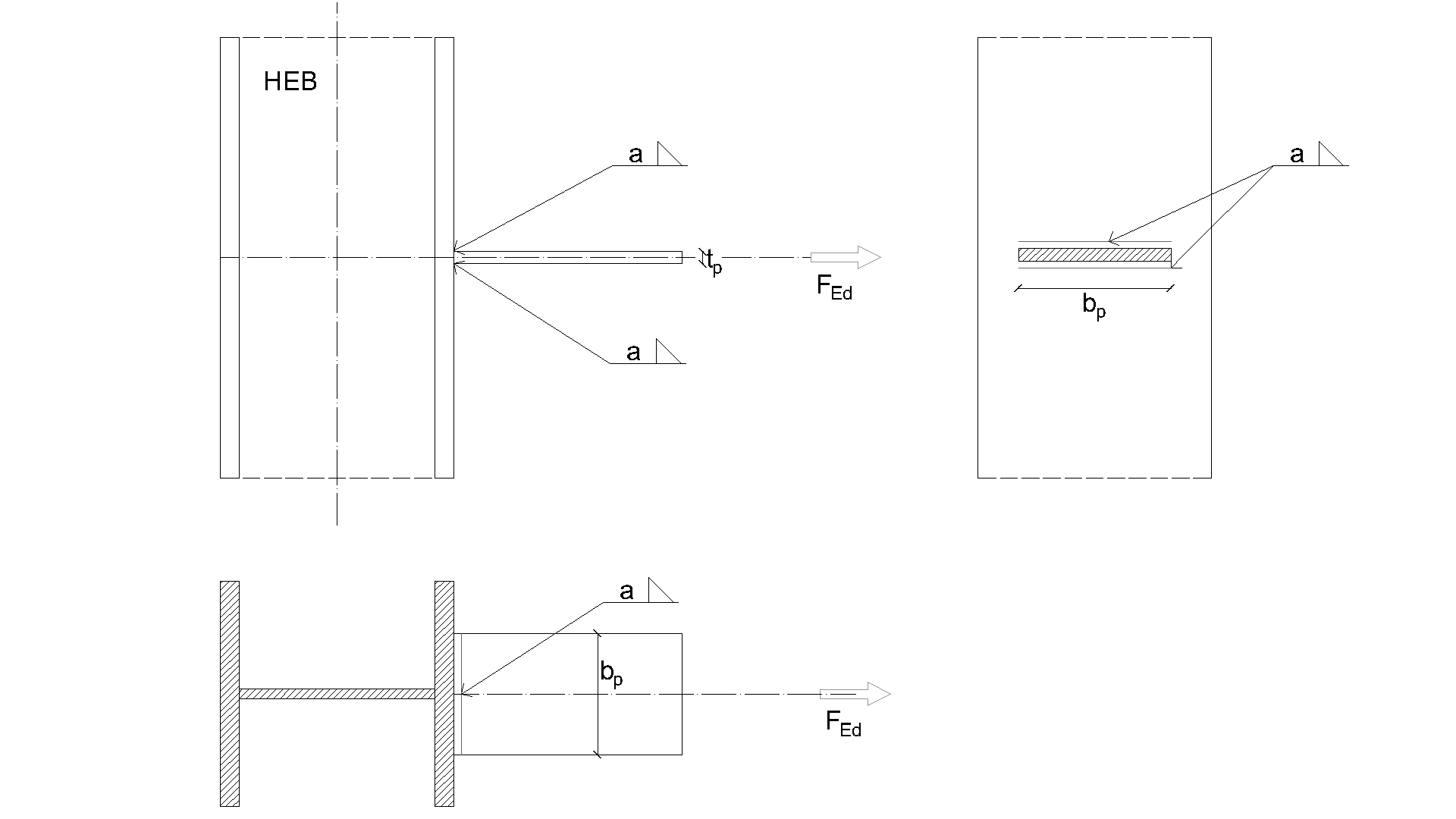
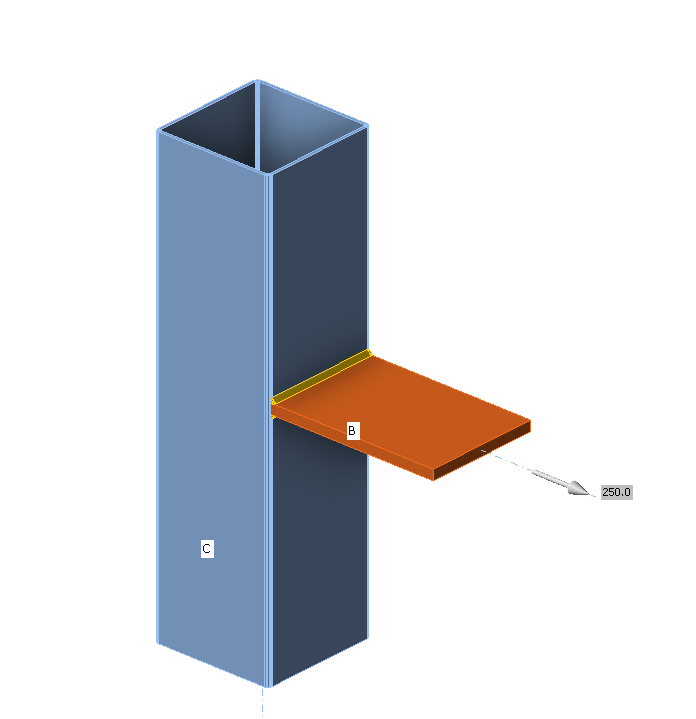
Weld, double fillet welds see Fig. 4.5.7
• Throat thickness aw = 5 mm
Outputs
• Design resistance in tension NRd = 68 kN
\[ \textsf{\textit{\footnotesize{Fig. 4.5.7 Benchmark example for the welded connection of plate to unstiffened column}}}\]