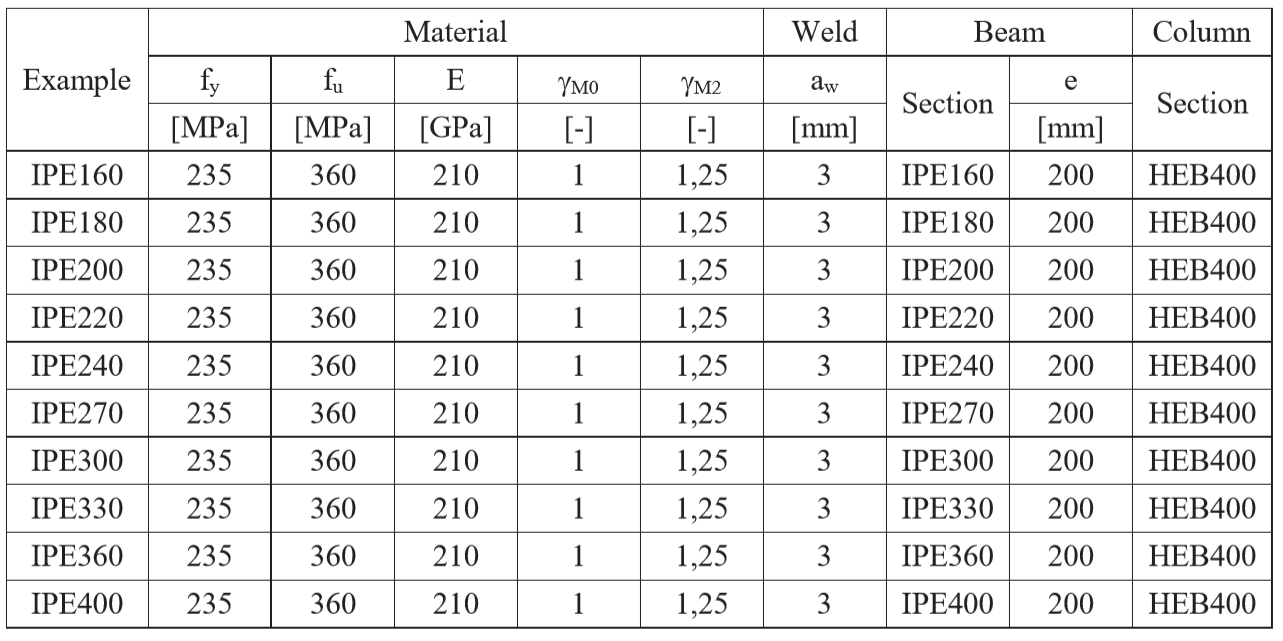
Fillet weld in beam to column joint
Description
The object of this chapter is verification of component based finite element method (CBFEM) for a fillet weld in a stiffened beam-to-column joint with component method (CM). An open section beam IPE is connected to open section column HEB400. The stiffeners are inside column opposite to beam flanges. The beam section is the changing parameter. Three load cases are considered, i.e. the beam is loaded in tension, shear and bending.
Analytical model
The fillet weld is the only component examined in the study. The welds are designed according to Chapter 4 in EN 1993-1-8:2005 to be the weakest component in the joint. The design resistance of the fillet weld is described in Section 4.1. Overview of the considered examples and the material are given in the Tab. 4.4.1. A geometry of the joint with dimensions is shown in Fig. 4.4.1.
Tab. 4.4.1 Examples overview
Hand Calculation of normal force N
\[\sqrt{ \sigma_{\perp}^2 + 3 \cdot \left( \tau_{\perp}^2 + \tau_{\parallel}^2\right)} \leq \frac{f_u}{\beta_{\mathrm{w}} \cdot \gamma_{\mathrm{M2}}}\]
\[\sigma_{\perp} = \tau_{\perp} = \frac{\sigma_{N}}{\sqrt{2}} = \frac{N}{l \cdot a}\cdot \frac{1}{\sqrt{2}} \]
\[ \tau_{\parallel} = 0\]
\[ \sqrt{ \left( \frac{\sigma_{N}}{\sqrt{2}} \right)^2 + 3 \cdot \left( \frac{\sigma_{N}}{\sqrt{2}} \right)^2} \leq \frac{f_u}{\beta_{\mathrm{w}} \cdot \gamma_{\mathrm{M2}}}\]
\[ \sqrt{ \left( \frac{N}{l \cdot a}\cdot \frac{1}{\sqrt{2}} \right)^2 + 3 \cdot \left( \frac{N}{l \cdot a}\cdot \frac{1}{\sqrt{2}} \right)^2} \leq \frac{f_u}{\beta_{\mathrm{w}} \cdot \gamma_{\mathrm{M2}}}\]
\[ N \leq \frac{f_{u} \cdot l \cdot a }{\beta_{\mathrm{w}} \cdot \gamma_{\mathrm{M2}} \cdot \sqrt{2}} \]
Where:
\(a\) - weld throat thickness
\(N\) - normal force acting on beam
\(l\) - total welds length
\(\beta_{\mathrm{w}}\) - correlation factor taken from EN 1993-1-8 Table 4.1
\(f_u\) - nominal ultimate tensile strength of the weaker part joined
\(\gamma_{\mathrm{M2}}\) - partial safety factor for welds
Hand Calculation of shear force V
The manual calculation presented in this chapter is predicated on certain assumptions. The shear force \(V\) is transmitted exclusively by the weld at the web. The bending moment resulting from the eccentricity of the force acting on the welds can be attributed to the flange welds. The weld section modulus of flange welds \(W\) is determined not by the distance measured from the centre of gravity of the welds, but from the edges of the flange to the beam centre of gravity, as calculated in practice.
The following equations demonstrate the derivation of the weld load-bearing capacity for shear force and bending moment according to the CM. The equivalent stress is specified in EN 1993-1-8, Equation (4.1). For the calculation of bending moment resistance, the plastic section modulus was assumed.
\[\sqrt{ \sigma_{\perp} + 3 \cdot \left( \tau_{\perp}^2 + \tau_{\parallel}^2\right)} \leq \frac{f_u}{\beta_{\mathrm{w}} \cdot \gamma_{\mathrm{M2}}}\]
\[V \le \min \left \{ \frac{f_\mathrm{u} \cdot l_V \cdot a}{\sqrt{3} \cdot \beta_{\mathrm{w}} \cdot \gamma_{M2}} , \, \frac{f_\mathrm{u} \cdot W}{\sqrt{2} \cdot \beta_{\mathrm{w}} \cdot \gamma_{\mathrm{M2}} \cdot e} \right \} \]
Where:
\(e\) - force eccentricity relative to the beam welds
\(a\) - weld throat thickness
\(V\) - shear force acting on beam
\(W= W_\mathrm{pl,flange}\) - welds section modulus
\(A_\mathrm{w,top,f} = B \cdot a\) - top flange edge weld area
\(A_\mathrm{w,bottom,f} = (B-t_\mathrm{w}) \cdot a\) - bottom flange edge weld area
\(z_\mathrm{w,top,f} = H / 2 \) - top flange edge weld lever arm
\(z_\mathrm{w,bottom,f} = (H - t_\mathrm{f}) / 2 \) - bottom flange edge weld lever arm
\(W_\mathrm{pl,flange} = 2 \cdot \left(A_\mathrm{w,top,f} \cdot z_\mathrm{w,top,f} + A_\mathrm{w,bottom,f} \cdot z_\mathrm{w,bottom,f}\right)\) - plastic flange section modulus
\(l_{\mathrm{V}}\) - total web welds length
\(\beta_{\mathrm{w}}\) - correlation factor taken from EN 1993-1-8 Table 4.1
\(f_\mathrm{u}\) - nominal ultimate tensile strength of the weaker part joined
\(\gamma_{\mathrm{M2}}\) - partial safety factor for welds
\(H\) - IPE beam height
\(B\) - IPE beam width
\(t_\mathrm{w}\) - IPE beam web thickness
\(t_\mathrm{f}\) - IPE beam flange thickness
Hand Calculation of bending moment M
In the calculation of bending moment without any interaction with shear force, the plastic section modulus of the whole weld section (both around flanges and around web) was assumed.
\[\sqrt{ \sigma_{\perp}^2 + 3 \cdot \left( \tau_{\perp}^2 + \tau_{\parallel}^2\right)} \leq \frac{f_u}{\beta_{\mathrm{w}} \cdot \gamma_{\mathrm{M2}}}\]
\[\sigma_{\perp} = \tau_{\perp} = \frac{\sigma_{N}}{\sqrt{2}} = \frac{M}{W}\cdot \frac{1}{\sqrt{2}} \]
\[ \tau_{\parallel} = 0\]
\[ \sqrt{ \left( \frac{\sigma_{N}}{\sqrt{2}} \right)^2 + 3 \cdot \left( \frac{\sigma_{N}}{\sqrt{2}} \right)^2} \leq \frac{f_u}{\beta_{\mathrm{w}} \cdot \gamma_{\mathrm{M2}}}\]
\[ \sqrt{ \left( \frac{M}{W}\cdot \frac{1}{\sqrt{2}} \right)^2 + 3 \cdot \left( \frac{M}{W}\cdot \frac{1}{\sqrt{2}} \right)^2} \leq \frac{f_u}{\beta_{\mathrm{w}} \cdot \gamma_{\mathrm{M2}}}\]
\[ M \leq \frac{f_{u} \cdot W }{\beta_{\mathrm{w}} \cdot \gamma_{\mathrm{M2}} \cdot \sqrt{2}} \]
\[ \sigma_{\perp} \leq \frac{f_{u} \cdot 0.9}{ \gamma_{\mathrm{M2}}} \]
\[ M \leq \frac{f_{u} \cdot W \cdot 0.9 \cdot \sqrt{2}}{ \gamma_{\mathrm{M2}} } \]
Where:
\(a\) - weld throat thickness
\(W \) - weld plastic section module
\(M\) - the bending moment acting on the beam
\(\beta_{\mathrm{w}}\) - correlation factor taken from EN 1993-1-8 Table 4.1
\(f_u\) - nominal ultimate tensile strength of the weaker part joined
\(\gamma_{\mathrm{M2}}\) - partial safety factor for welds
Numerical model
The weld component in CBFEM is described in General theoretical background and EN theoretical background.
Nonlinear elastic-plastic material is used for welds in this study. The limit plastic strain is reached in longer part of the weld and stress peaks are redistributed.
\[ \textsf{\textit{\footnotesize{Fig. 4.4.1 Joint’s geometry with dimensions}}}\]
Verification of resistance
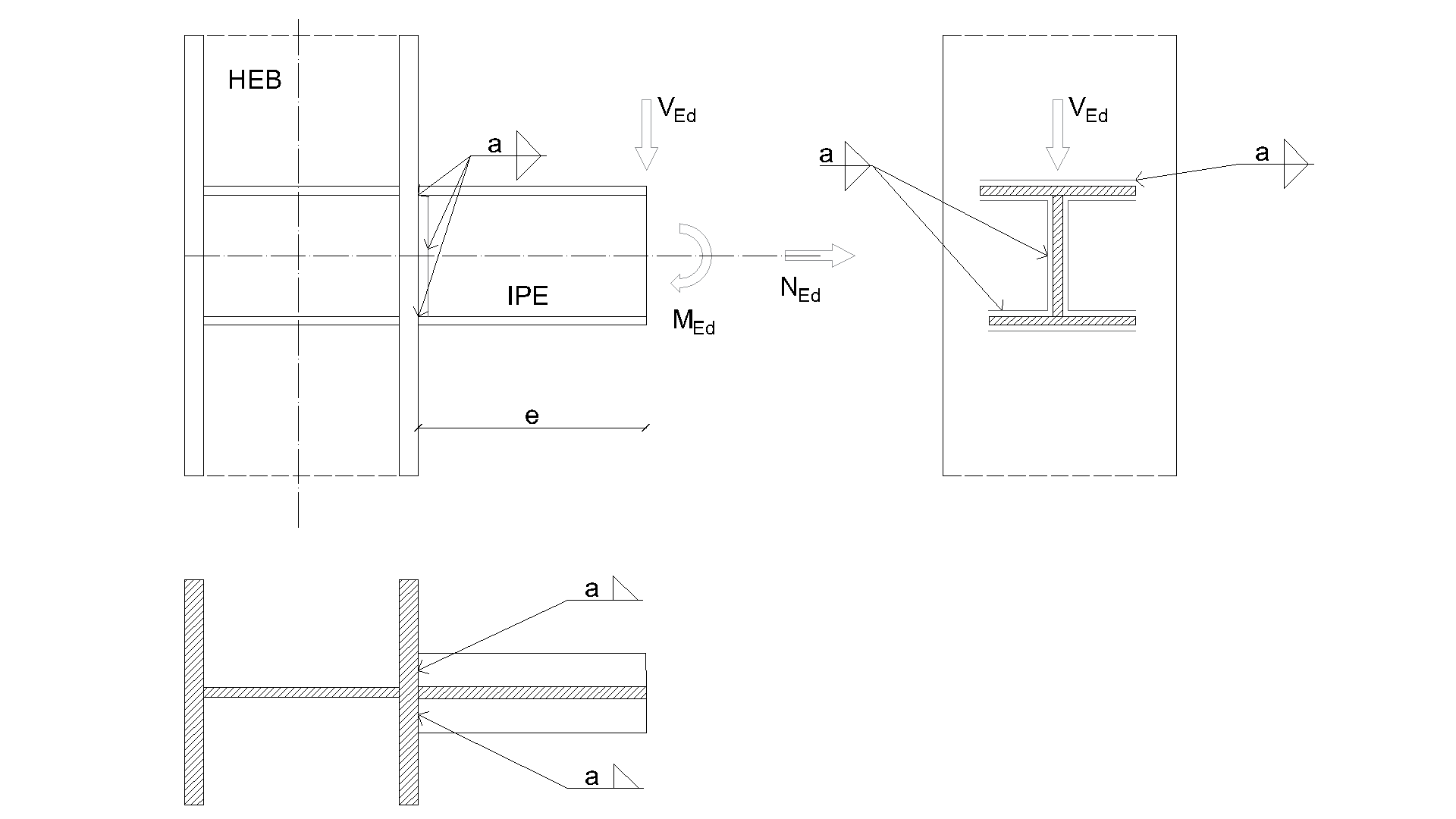
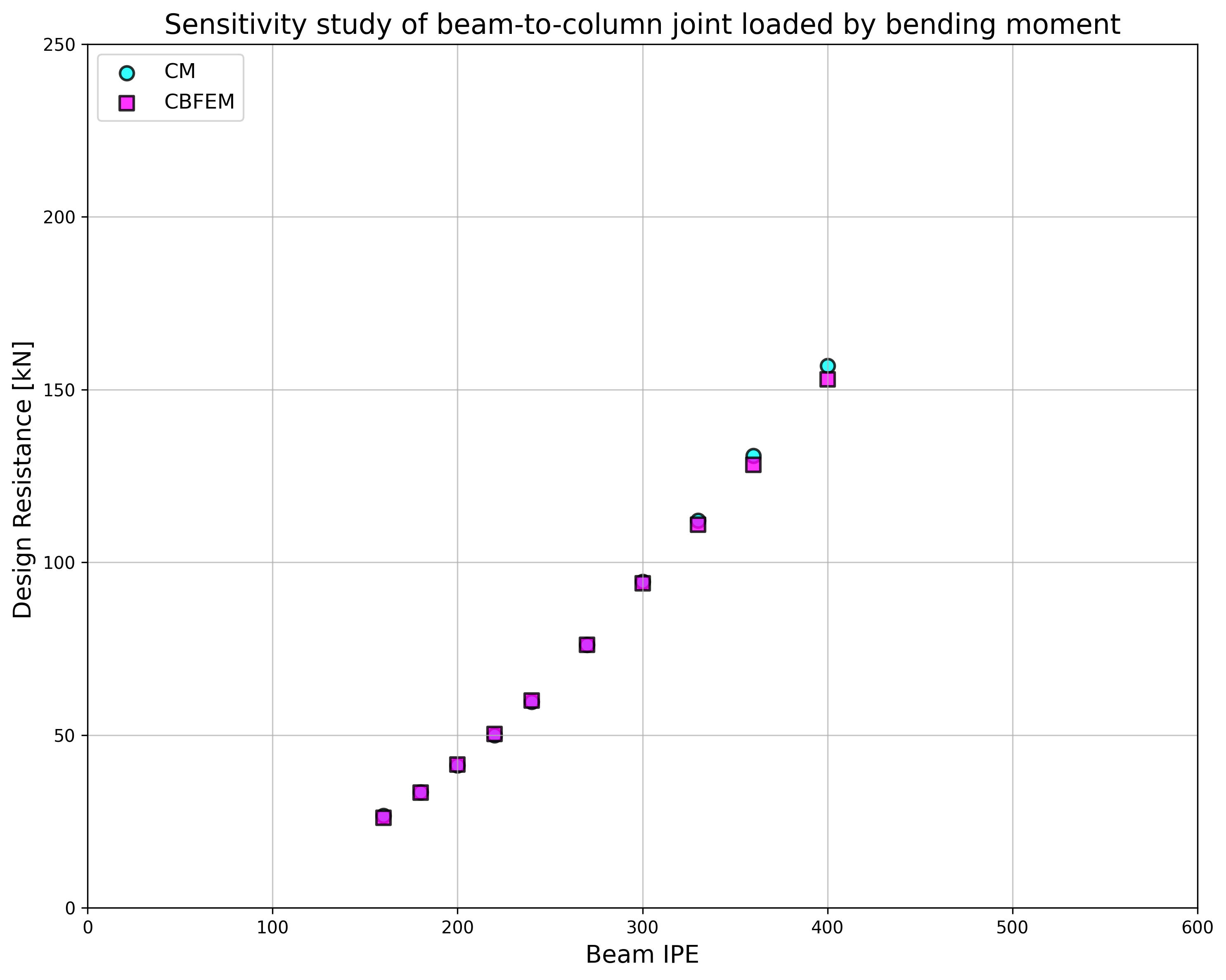
Design resistance calculated by CBFEM Idea RS software is compared with the results of CM. The weld’s design resistances are compared, see Tab. 4.4.2. The study is performed for one parameter beam section and three load cases: normal force NEd, shear force VEd, and bending moment MEd.
Tab. 4.4.2 Comparison of CBFEM and CM
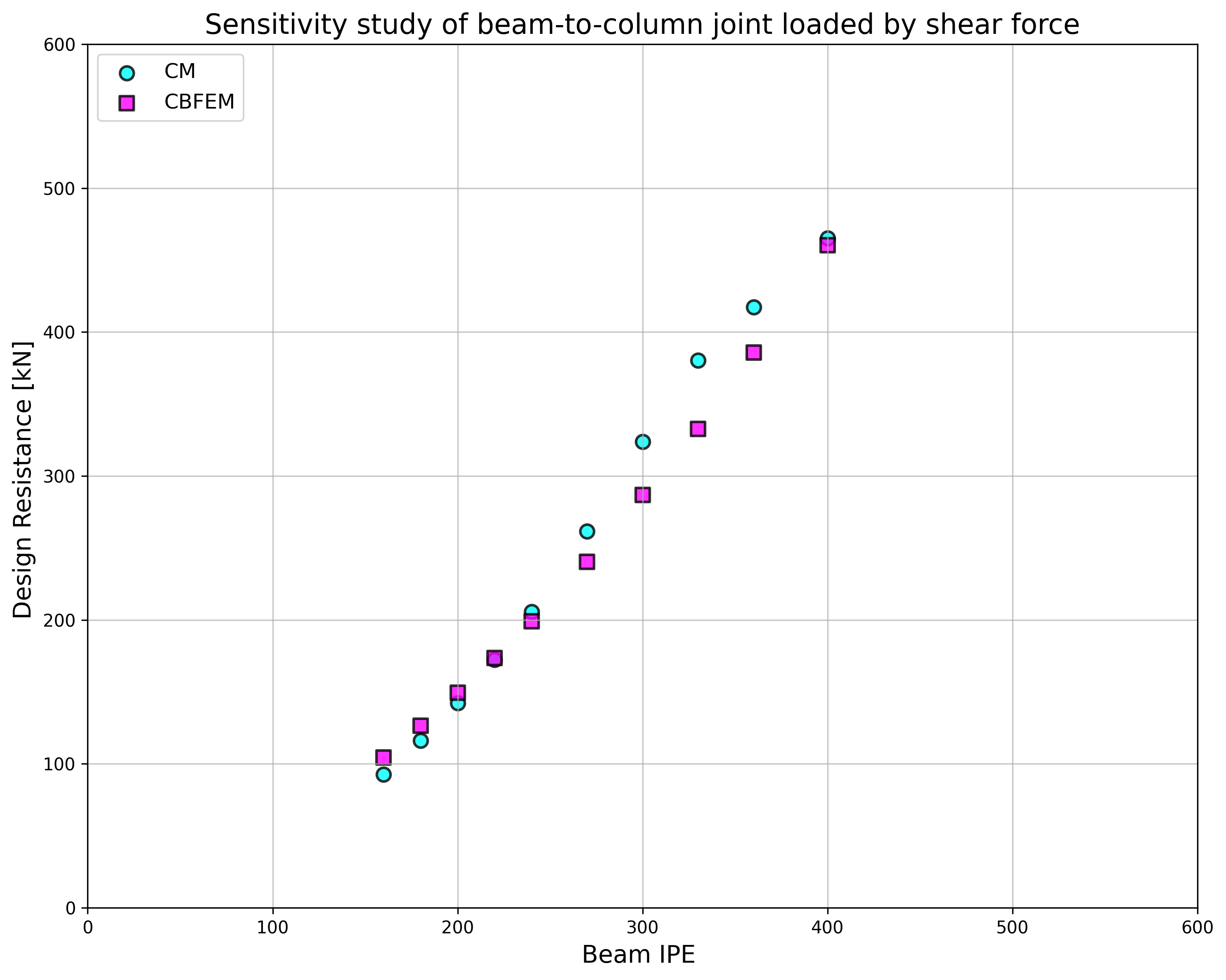
Results of CBFEM and CM are compared and a sensitivity study is presented. The influence of beam cross-section on the design resistance a welded beam-to-column joint loaded in tension is shown in Fig. 4.4.2, in shear in Fig. 4.4.3 and in bending in Fig. 4.4.4. The study shows good agreement for all applied load cases.
\[ \textsf{\textit{\footnotesize{Fig. 4.4.2}}}\]
\[ \textsf{\textit{\footnotesize{Fig. 4.4.3}}}\]
\[ \textsf{\textit{\footnotesize{Fig. 4.4.4}}}\]
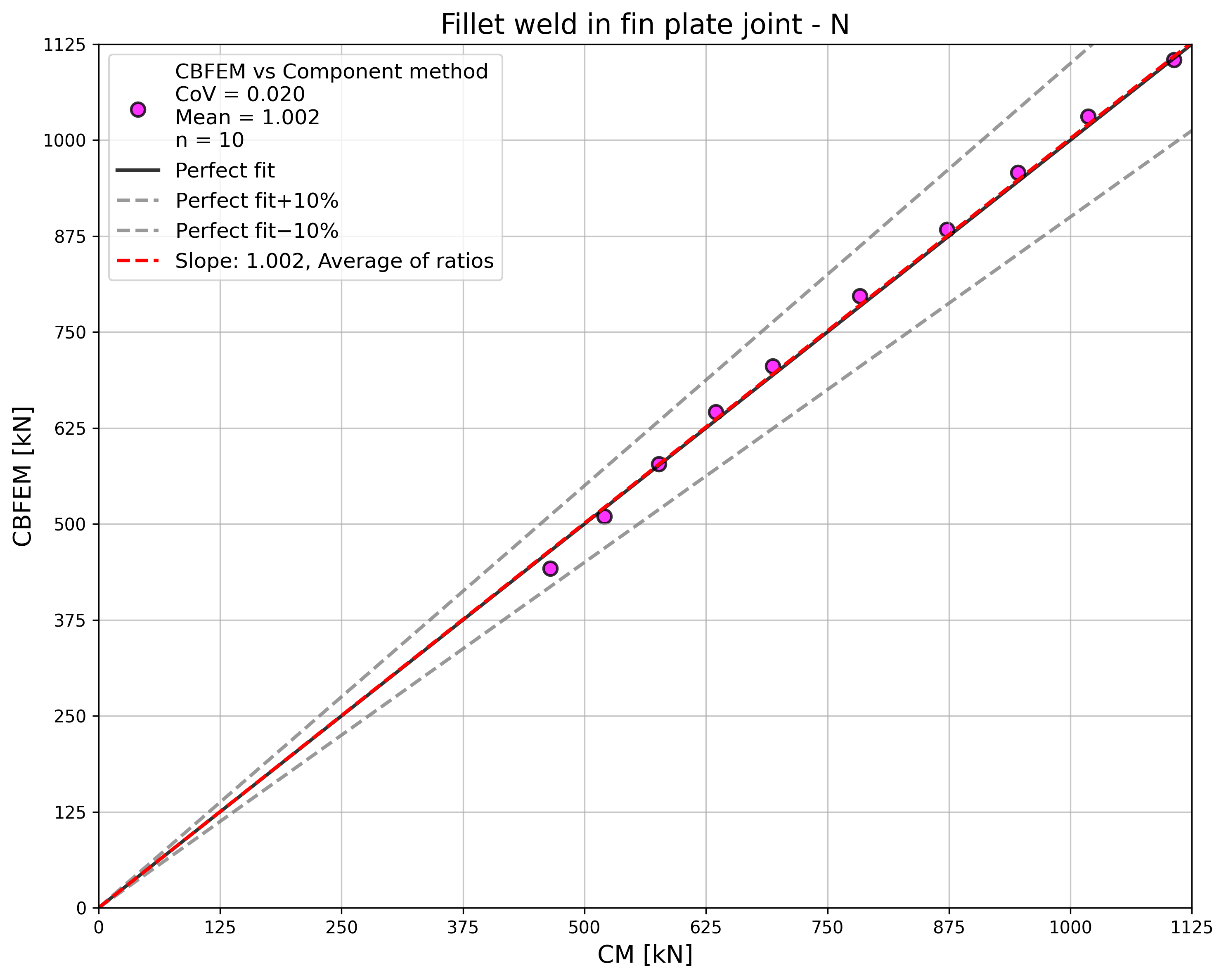
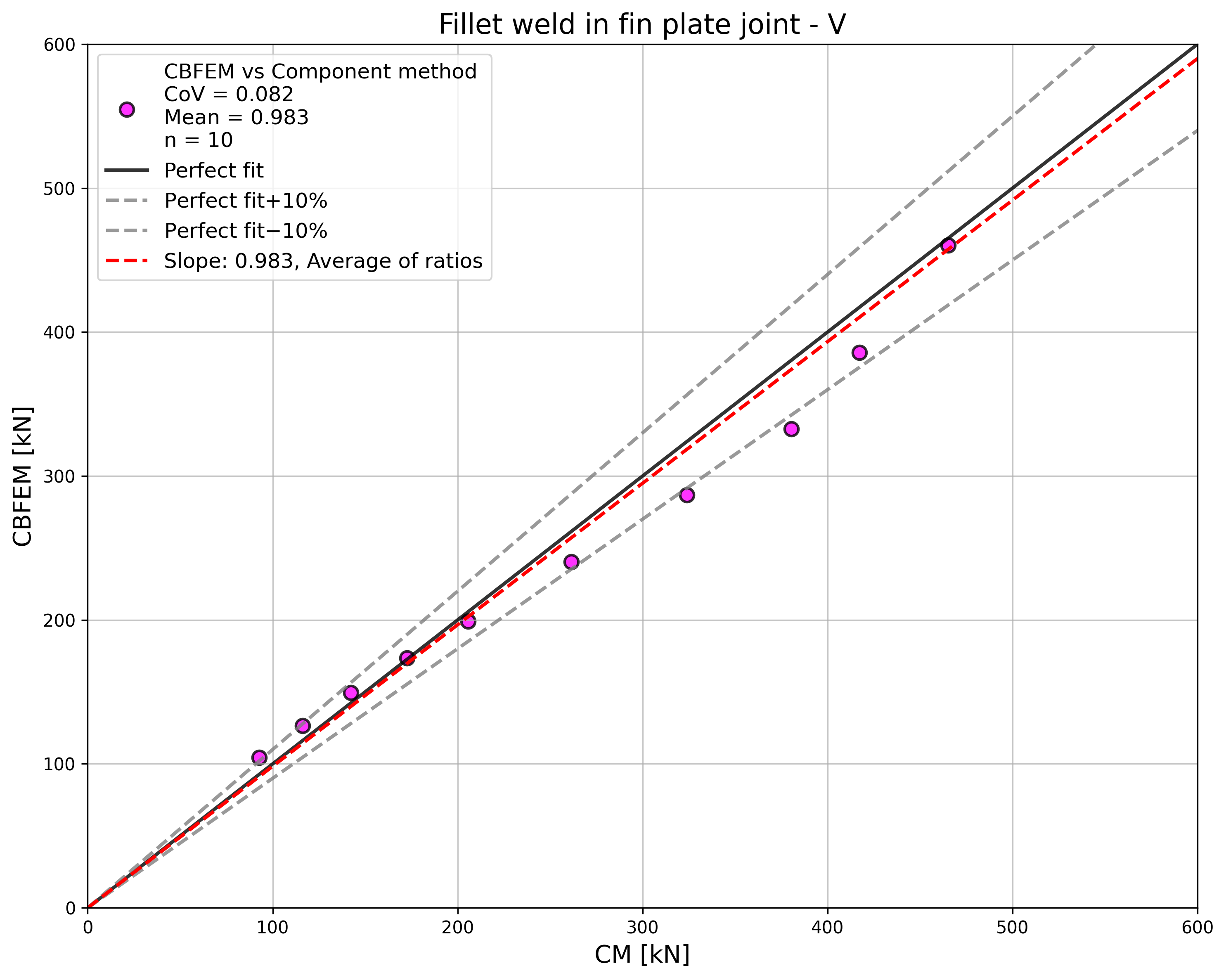
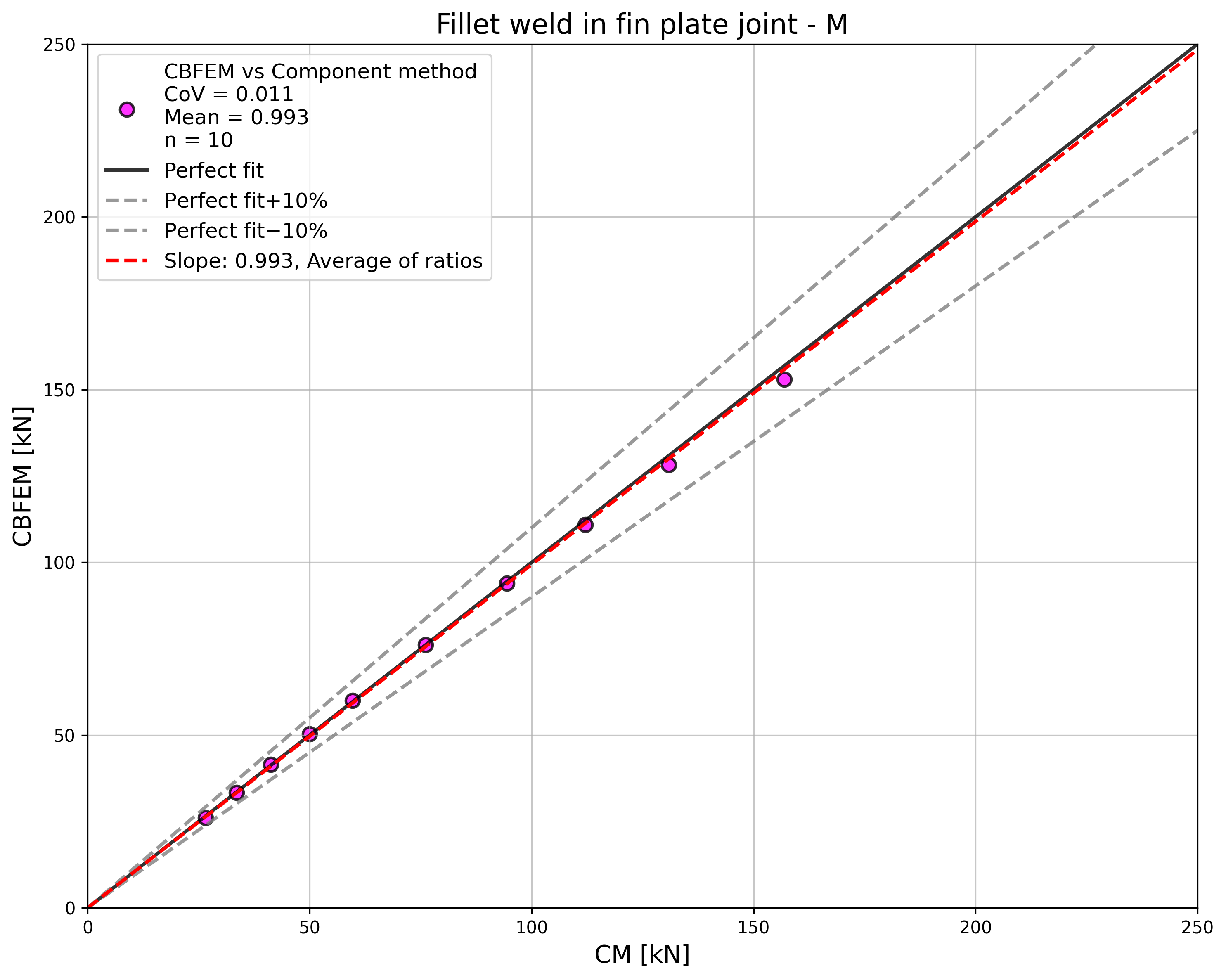
To illustrate the accuracy of the CBFEM model, results of the sensitivity study is summarized in a diagram comparing CBFEM’s and CM’s design resistances, see Fig. 4.4.5. The results show that the difference of the two calculation methods is in all cases less than 10%.
\[ \textsf{\textit{\footnotesize{Fig. 4.4.5 Verification of CBFEM to CM}}}\]
Benchmark example
Inputs
Column
- Steel S235
- HEB 400
Beam
- Steel S235
- IPE 160
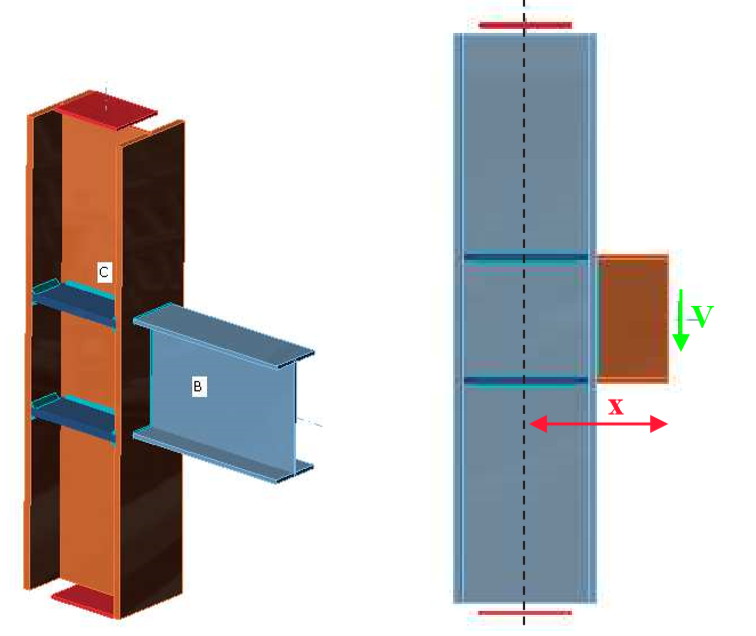
- Force eccentricity to weld x = 400 mm, see Fig. 4.4.6
Weld
- Throat thickness aw = 3 mm
Outputs:
- Design resistance in shear VRd = 105 kN
\[ \textsf{\textit{\footnotesize{Fig. 4.4.6 Benchmark example of the welded beam to column joint with force eccentricity}}}\]