No que diz respeito à rotura frágil, a verificação do corte é uma das verificações importantes de uma secção de betão armado.
Procedimento de cálculo
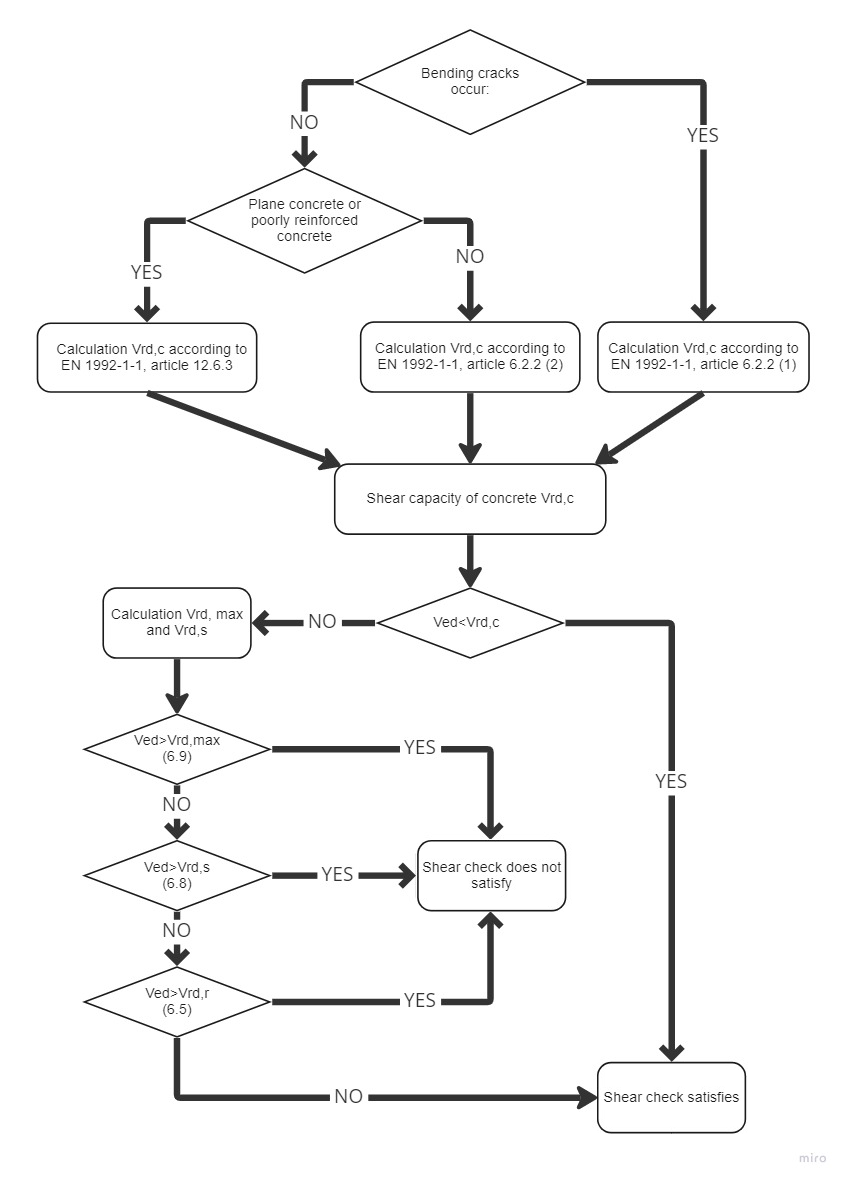
O cálculo da resistência ao cisalhamento é composto por várias partes básicas. Em primeiro lugar, deve-se analisar se as fissuras devidas à flexão ocorrem ou não no local verificado.Se existirem, utiliza-se o cálculo de acordo com a EN 1992-1-1[2], Artigo 6.2.2 (1).Caso contrário, determina-se se se trata de betão plano ou de betão mal armado e, em seguida, procede-se de acordo com a norma EN 1992-1-1, artigo 12.6.3.
No caso do betão armado não fissurado (sem armadura de corte), procede-se à verificação de acordo com a norma EN 1992-1-1, artigo 6.2.2 (2) Para Elementos, onde é necessária uma armadura de cisalhamento, verificamos de acordo com o Artigo 6.2.3[2].
\[ \textsf{\textit{\footnotesize{\qquad Diagrama de processo para verificação de corte.}}\]
Resistência ao corte de barras sem armadura de corte
Resistência ao corte de barras em zonas de flexão fendilhadas (art. 6.2.2 (1)[2])
A resistência ao corte de elementos de betão armado sem armadura de corte sujeitos a momento fletor é dada por
\[{{V}_{Rd,cm}}=~{{C}_{Rd.c}}k~{{\left( 100~{{\varrho }_{l}}{{f}_{ck}} \right)}^{{}^{1}/{}_{3}}}~{{b}_{w}}d\]
A qual foi definida com base em ensaios efectuados num número representativo de vigas simples em caso de rotura por força de corte. Uma vez que a resistência acima pode ser nula para elementos sem armadura longitudinal (rl), para elementos mal armados foram derivadas equações. Uma vez que a resistência acima pode ser nula para elementos sem armadura longitudinal (rl), para os elementos mal armados foi determinada pela equação
\[{{V}_{Rd,c}}\ge ~{{\upsilon }_{min}}{{{b}_{w}}d\]
Para a resistência ao corte com influência da força normal foi determinada pela equação
\[{{V}_{Rd,cn}}=~{{k}_{1}}{{\sigma }_{cp}}~{{b}_{w}}d\]
Resistência ao corte na sua expressão completa que corresponde à EN 1992-1-1 art. 6.2.2 (1)
\[{{V}_{Rd,c}}=~\left[ {{C}_{Rd.c}}k~{{\left( 100~{{\varrho }_{l}}{{f}_{ck}} \right)}^{{}^{1}/{}_{3}}}+{{{k}_{1}}{{\sigma }_{cp}} \right]~{{b}_{w}}d\]
Com o mínimo de
\[{{V}_{Rd,c}}=~\left( {{\upsilon }_{min}}+{{k}_{1}}{{\sigma }_{cp}} \right){{b}_{w}}d\]
em que
CRd,c = 0,18 / γc,
k fator de altura da secção transversal
\[k=1+\sqrt{\frac{200}{d}}<2,0\]
ρ1 taxa de armadura para armadura longitudinal
\[{{\varrho }_{l}}=\frac{{{A}_{sl}}}{{{b}_{w}}d}\le 0,02\]
fck resistência caraterística à compressão cilíndrica do betão aos 28 dias
k1 = 0,15
σcp =NEd /Ac < 0,2 fcd v MPa
bw largura mais pequena da secção transversal na zona de tração
d profundidade efectiva de uma secção transversal
υmin resistência mínima ao cisalhamento equivalente υmin = 0,035 k3/2 fck1/2
Resistência ao corte de barras em zonas de flexão não fendilhadas (art. 6.2.2 (2)[2])
A resistência ao corte de barras em zonas de flexão não fendilhadas pode ser determinada a partir do círculo de Mohr. Na equação
\[{{\sigma }_{1,2}}=\frac{{{\sigma }_{x}}+{{\sigma }_{y}}}}{2}\pm \sqrt{{{\left( \frac{{\sigma }_{x}}-{{\sigma }_{y}}}}{2} \right)}^{2}}+\tau _{z}^{2}}\]
Substituímos σx = σcp a τz= VRd,c S / (I bw) e calculamos VRd,c e obtemos a equação correspondente à fórmula dada na EN 1992-1-1 art. 6.2.2 (2)
em que
I é o segundo momento da área,
bw é a largura da secção transversal no eixo centroidal
S é o primeiro momento da área acima e em torno do eixo centróide,
fctd resistência à tração axial de projeto do betão, em MPa,
scp é a tensão de compressão do betão no eixo centroidal devida à carga e/ou ao pré-esforço,
al fator de comprimento de transmissão, geralmente 1,0.
Em relação ao que precede, deve notar-se que, em zonas sem fissuras de flexão, aresistência VRd,c pode ser significativamente mais elevada do que nas zonas fissuradas, de acordo com o artigo 6.2.2 (1)[2]. A figura abaixo mostra claramente que, embora a força de corte seja verificada no seu extremo (o que não produz fissuras), não precisa necessariamente de garantir que será transferida ao longo de todo o comprimento da viga.Isto deve-se a uma alteração no método de cálculo da resistência ao corte do betão.Por segurança, é claro que a resistência ao cisalhamento pode ser considerada de acordo com o Artigo 6.2.2 (1)[2] também em locais onde não ocorrerão fissuras.
\[ \textsf{\textit{\footnotesize{\qquad Comparação da resistência ao corte antes e depois da ocorrência de fendas.}}}\]
Para a expressão de VRd, c de acordo com o Artigo 6.2.2 (2)[2] também deve ser notado que, no caso geral, deve ser baseado na verificação na fibrada tensão de tração principal extrema do betão na zona de tensão de compressão normal, mas não no centro de gravidade da secção.Nesta altura, é necessário calcular as caraterísticas da secção transversal (S e bW).Para determinar a tensão principal máxima s1 no programa IDEA RCS, traçamos uma linha através do centro de gravidade na direção das forças de corte resultantes.Esta linha é dividida em 20 sectores e nesta linha serão apresentados mais pontos caraterísticos (pontos do polígono da secção transversal, centro de gravidade, eixo neutro).Dentro destes pontos, calculamos S, bw, σx, τyz a σ1. No ponto de tensão de tração principal máxima, calcula-se a resistência ao corte.
A força de corte antes de aplicar o fator de redução b requerido pelo Artigo 6.2.2 (6) deve satisfazer a condição extra
\[ {{V}_{Ed}}\le 0,5~{{b}_{w}}d~\upsilon ~{{f}_{cd}}\]
em que
\ [ {{ υ}}\le 0,6\left[ 1-\frac{{{f}_{ck}}}{250} \right]\] kde fck je v MPa
Resistência ao corte de barras sem armadura ou ligeiramente armadas (art. 12.6.3[2])
A resistência ao corte para betão simples ou ligeiramente armado pode ser determinada a partir da expressão
\[ {{\tau }_{cp}}\le k~{{V}_{Ed~}}/{{{A}_{cc}}\]
Onde
τcp substituímos por
\[ {{f}_{cvd}}=\sqrt{f_{ctd,pl}^{2}+{{\sigma }_{cp}}{{f}_{ctd,pl}}}~pro~{{\sigma }_{cp}}\le {{\sigma }_{c,lim}}~\]
ou
\[ {{f}_{cvd}}=\sqrt{f_{ctd,pl}^{2}+{{{\sigma }_{cp}}{{f}_{ctd,pl}}-{{\left( \frac{{\sigma }_{cp}}-{{\sigma }_{c,lim}}}}}{2} \right)}^{2}}}~pro~{{\sigma }_{cp}}>{{{\sigma }_{c,lim}}~\]
Os valores parciais utilizados na fórmula acima são dados por:
\[ {{\sigma }_{c,lim}}={{f}_{cd,pl}}-2\sqrt{{f}_{ctd,pl}}\left( {{f}_{ctd,pl}}+{{f}_{cd,pl}} \right)}\]
em que
fcd,pl Resistência à compressão de projeto para betão simples ou ligeiramente armado,
fctd,pl Resistência à tração axial de projeto do betão simples ou ligeiramente armado,
fcvd Resistência ao corte de projeto sob compressão do betão.
A resistência dos elementos com armadura de corte (art. 6.2.3[2])
O cálculo da resistência das barras de betão armado com armadura de corte é baseado no método da analogia da treliça com diagonais de ângulo variável.A base deste método é o equilíbrio de forças no triângulo determinado pela força da escora (diagonal), a força da armadura de corte (estribo) e a força da armadura longitudinal.
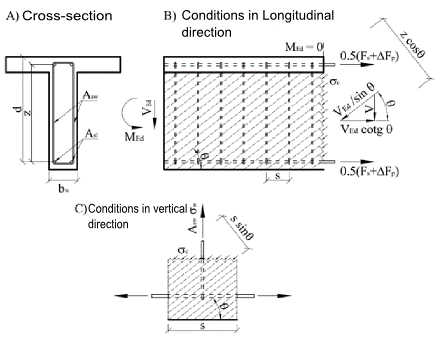
\[ \textsf{\textit{\footnotesize{\qquad Principe of Truss analogy for member under shear load.}}}\]
A secção transversal sob carga de corte é quebrada por fendas num ângulo θ, por esta razão a diagonal de betão com o mesmo ângulo que as forças de corte resiste à força de corte. A força de compressão da diagonal pode ser expressa como Ved/sinθ. Esta força deve ser transferida pela superfície do betão, perpendicular à diagonal de compressão bwzcosθ. A tensão de tração do betão na diagonal de compressão é então igual:
\[ {{\sigma }_{c}}=\frac{{{V}_{Ed}}}{{{b}_{w}}z~\sin \text{ }\!\!\theta\!\!\text{ }\cos \theta }=\frac{{V}_{Ed}}}{{{b}_{w}}z}\left( \tan \theta +\cot \theta \right)\]
Substituindo \ [{{\sigma }_{c}}={{{\alpha }_{cw}}{{\nu }_{1}}{{{f}_{cd}}\] e \ [{{V}_{Ed}}={{{V}_{Rd,max}}\] e expressando \ [{{V}_{Rd,max}}\] obtemos a equação para a resistência ao corte da diagonal:
\[ {{V}_{Rd,max}}=~{{\alpha }_{cw}}~{{b}_{w}}~z~{{\nu }_{1~}}{{f}_{cd}}/\left( \cot \theta +\tan \theta \right)\]
Para equilibrar a componente da força vertical na diagonal de compressão, será utilizada uma armadura de corte.A dimensão da força vertical é baseada na tensão de compressão diagonal na área de betãoárea de betão que corresponde a um único estribo - \ [{{\sigma }_{c}}{{{b}_{w}}s{{\sin }^{2}}\theta\]. A força limite do estribo é dada como \ [{{A}_{sw}}{{{f}_{ywd}}/s\].
Inserindo σc, comparando com a força limite na armadura, após modificações obtemos:
\[ \frac{{{A}_{sw}}{{f}_{ywd}}}{s}=\frac{{{V}_{Ed}}}{z}\tan \theta\]
Em seguida, expressando Ved como VRDs, obtemos a resistência da secção com armadura de corte vertical:
\[ {{V}_{Rd,s}}=~\frac{{{A}_{sw}}}{s}z~{{f}_{ywd}}\cot \theta\]
A força de corte longitudinal é transferida pela armadura longitudinal e pode ser determinada como Vedcotgθ. A derivação das fórmulas acima pode ser encontrada em[4].
Utilizando o programa IDEA RCS, é possível verificar apenas barras com armadura de corte vertical. Em geral, podem ser utilizadas as seguintes equações:
\[{{V}_{Rd,s}}=~\frac{{{A}_{sw}}}{s}z~{{f}_{ywd}}\left( \cot \theta +\cot \alpha \right)\sin \alpha\]
\[{{V}_{Rd,max}}=~{{\alpha }_{cw}}~{{b}_{w}}~z~{{\nu }_{1~}}{{f}_{cd}}\left( \cot \theta +\cot \alpha \right)/\left( 1+{\cot }^{2}}\theta \right)\]
Em que
Asw é a área da secção transversal da armadura de corte,
s é o espaçamento dos estribos,
fywd é a tensão de cedência de projeto da armadura de corte,
bw é a largura mínima entre as cordas de tração e de compressão. Para calcular a resistência VRd,max , o valor da largura da secção deve ser reduzido para a chamada largura nominal da secção transversal, no caso de a secção transversal ser enfraquecida por condutas de cabos
bw,nom=bw-0,5ΣΦ para condutas metálicas betumadas
bw,nom=bw-1,2ΣΦ para condutas metálicas não betumadas
υ = 0,6 pro fck ≤ 60MPa ou pro fck > 60MPa,
αcw é um coeficiente que tem em conta o estado da tensão na corda de compressão.
| Carga | σcp = 0 | 0 <σcp≤0,25fcd | 0,25fcd <σcp≤0,5fcd | 0,5fcd <σcp≤1,0fcd |
| Coeficienteacw | 1,0 | 1+σcp/fcd | 1,25 | 2,5(1 - σcp/fcd) |
Tab. 1-1 Coeficiente de determinação αcw
O ângulo θ é o ângulo entre a escora de compressão do betão e o eixo da viga perpendicular à força de corte. Os valores limite de cotθ para utilização num país podem ser consultados no respetivo Anexo Nacional. Os limites recomendados são dados pela expressão:
\[1~\le ~\cot \theta \le 2,5\]
A escolha do tamanho do ângulo θ pode afetar o valor das resistências. A dependência das resistências é visível na Figura 1.15 A figura mostra que, com o aumento do ângulo θ, a resistência VRd,max aumenta e a resistência VRd,s diminui. A resistência VRd,c é constante, uma vez que se baseia no método da analogia da treliça.
\[ \textsf{\textit{\footnotesize{\qquad Dependência entre a resistência ao corte e o ângulo q.}}}\]
Cálculo das caraterísticas da secção para o corte
Para calcular o corte, é importante calcular as variáveis da secção que afetam a resistência ao corte.Estas variáveis incluem principalmente a largura da secção resistente ao corte bw, a profundidade efetiva d e o braço de alavanca z. O código[2] fornece estes valores que se correlacionam diretamente com a tensão de flexão real.Mas o problema é determinar estes valores quando a direção dos momentos flectores resultantes (ou mais precisamentea direção da resultante da resistência da secção) é significativamente diferente da direção das forças de corte resultantes.Neste caso, o código EC2 não fornece quaisquer recomendações.
Largura da secção transversal que resiste ao corte bw
O programa IDEA RCS calcula a largura da secção transversal resistente ao corte na direção perpendicular à resultante das forças de corte.Dependendo do artigo do Eurocódigo, esta largura é calculada como
- A menor largura da secção entre a resultante de compressão do betão e a armadura de tração na direção perpendicular à resultante das forças de corte para o artigo 6.2.2 (a) e 6.2.3 (1)
- A largura da secção numa direção perpendicular à resultante das forças de corte no ponto verificado de acordo com o artigo 6.2.2 (2)
Profundidade efectiva de uma secção transversal
A profundidade efectiva é normalmente definida como a distância da fibra de betão mais comprimida ao centro de gravidade da armadura.Uma vez que está diretamente relacionada com a flexão, a distância é dada como projeção perpendicular à linha de gravidade da deformação plana.
Esta definição pode ser clarificada de modo a que, em vez do centro de gravidade da armadura de tração, seja utilizada a posição da resultante das forças da armadura.Durante o desenvolvimento do programa IDEA RCS, o problema foi resolvido:como definir a profundidade efectiva da secção transversal, para a qual o plano das cargas de flexão não corresponde à direção das forças de corte resultantes.Assim, a profundidade efectiva é definida como a distância da fibra de betão mais comprimida às forças resultantesna armadura de tração (com base na tensão de flexão) e na direção das forças de corte resultantes, ver Figura 1.17.
Casos excepcionais ocorrerão se não for possível determinar a fibra comprimida ou a resultante na armadura de tração. Neste caso, recomenda-se a utilização do valor 0.9 h (90% da profundidade da secção na direção das forças de corte resultantes). Este valor pode ser definido pelo utilizador no programa IDEA RCS através da definição de variáveis de código.
Braço de alavanca das forças internas
O braço de alavanca das forças internas está em 6.2.3 (3)[2] e é definido como a "distância entre as cordas de tração e compressão". A norma não define como proceder quando o plano do momento fletor atuante é diferente da direção das forças de corte resultantes.Portanto, como no caso da profundidade efectiva, definimos a distância na direção das forças de corte resultantes.Também aqui, podemos enfrentar casos de exceção semelhantes, por exemplo, toda a secção está sob compressão, etc. Neste caso, tomamos o valor 0,9 d (90% da altura efectiva da secção). Este valor, o utilizador pode definir no programa IDEA RCS através da definição de variáveis de código.
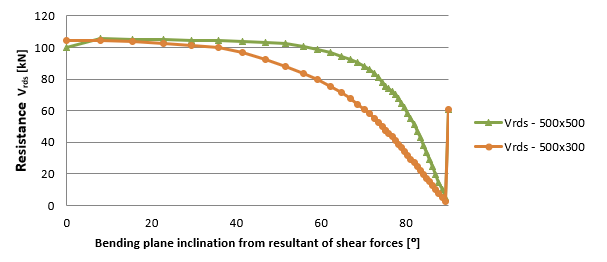
A dependência entre a inclinação do plano de flexão e a resultante da força de corte é claramente visível na Figura 1.18 e na Figura 1.19.19. Com o aumento da inclinação, os valores da altura efectiva, dos braços de alavanca e das resistências relacionadas diminuem. O estado limite é 90°. Para esta inclinação, o braço de alavanca das forças internas não pode ser calculado, pelo que o braço de alavanca é igual a zero. Neste caso, é considerado o valor especificado na definição das variáveis de código. Desta forma, existe um salto no final do gráfico. Este estudo prova que o máximo recomendado para a inclinação é de cerca de 20°.
\[ \textsf{\textit{\footnotesize{\qquad Dependência entre a profundidade efectiva, o braço de alavanca para a inclinação do plano de flexão e a resultante das forças de corte.}}}\]
\[ \textsf{\textit{\footnotesize{\qquad Dependência entre a resistência Vrds para a inclinação do plano de flexão e a resultante do corte.}}}\]
Como parte dos testes da aplicação RCS, foi realizado um estudo sobre a dependência da resistência ao corte com a alteração da força normal. A resistência VRd,max é afetada apenas pelo coeficiente αcw, ver Fig. 1.20. 1.20. A Fig. 1.21 mostra um valor constante da resistência VRds. Para a resistência VRdc, as diminuições causam o aumento da força normal.A curva azul da Fig. 1.21 mostra a resistência VRdc, negligenciando a influência das fissuras, e foi calculada utilizando a fórmula da secção 6.2.2 (1)[2] O salto na transição entre pressão e tração é causado pela contribuição da armadura de tração. A curva vermelha é calculada utilizando a fórmula da secção 6.2.2 (2)[2]. Após a ocorrência da primeira fissura, a curva de dependência é a mesma que para 6.2.2 (1)[2].
\[ \textsf{\textit{\footnotesize{\qquad Curva de dependência da resistência ao corte VRd,max para a força normal.}}}\]
\[ \textsf{\textit{\footnotesize{\qquad Dependência das resistências ao corte VRd,c a VRd,s em relação à força normal.}}}\]