Ontwerpen van D-gebieden in brugconstructies met CSFM

De Compatible Stress Field Method (CSFM) is ontwikkeld op basis van klassieke theorieën en gangbare ontwerpmethoden, maakt een hoge mate van automatisering mogelijk en is in overeenstemming met de geldende ontwerpnormen.

Voor betondoorsneden waarop de Bernoulli-Navier-hypothese van behoud van vlakheid na vervorming geldt (B-gebieden), kunnen standaard ontwerpprocedures worden toegepast. Gebieden waar deze hypothese niet van toepassing is, worden aangeduid als discontinuïteitsgebieden (D-gebieden). Dit betreft onder andere constructiedelen met geconcentreerde belastingen, abrupte veranderingen in de doorsnede en openingen. In de bruggenbouw zijn dit bijvoorbeeld pijlerkoppen, dwarsbalken met openingen en tandopleggingen.

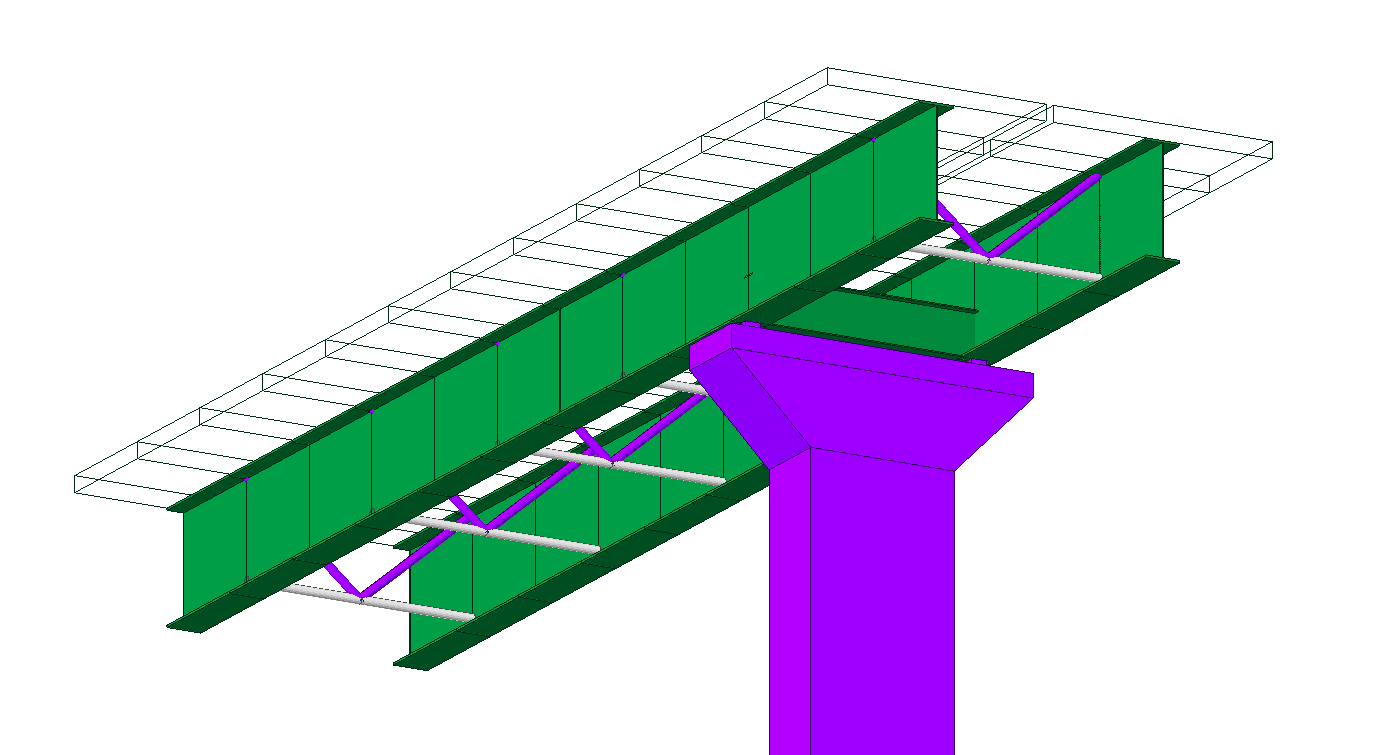
Fig. 1. Pijlerhoofd van een spoorbrug - berekeningsmodel in Midas Civil

Tijdrovende staafwerkmodellen

Momenteel worden het Strut-and-Tie model en het Stress Field model het meest toegepast voor de dimensionering van D-gebieden. Bij het opstellen van een staafwerkmodel wordt aangenomen dat de treksterkte van beton verwaarloosbaar is. Op basis hiervan wordt een eenvoudig vakwerkmodel van het gedrag van het D-gebied in de uiterste grenstoestand geconstrueerd, bestaande uit elementen die in druk en trek werken.

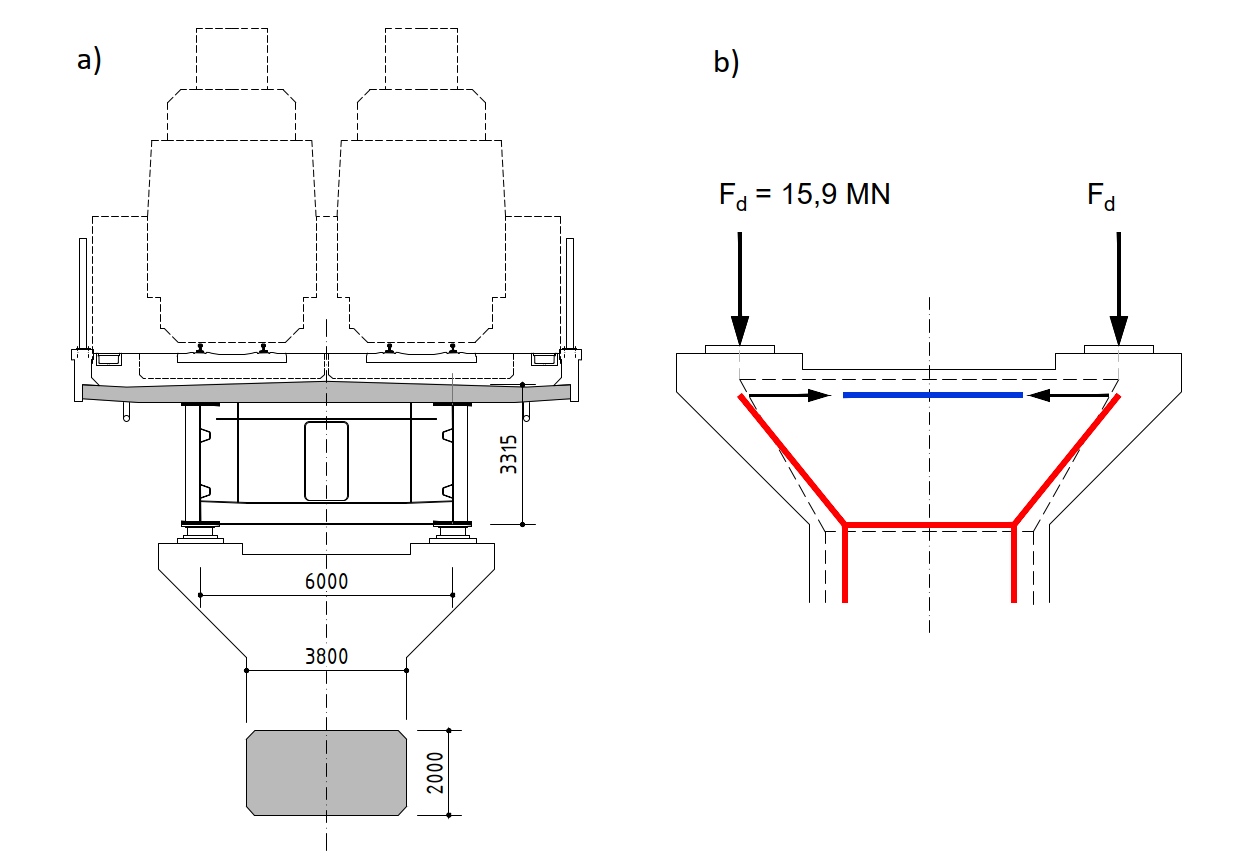
Een voorbeeld van een typische D-gebied bij een bruggenhoofd is weergegeven in Fig. 1 en 2. In principe vormt dit geen complex probleem, en het definiëren van een basis S&T-model met één hoofddwarsbalk (Fig. 2b) zou geen uitdaging moeten zijn voor een brugconstructeur. Toch kan zelfs deze basistaak, bij correcte beoordeling volgens de ontwerpnorm, een tijdrovend, handmatig en iteratief proces zijn.

Afbeelding 2. Pijlerhoofd van een spoorbrug: a) dwarsdoorsnede op de pijlerlocatie; b) vervangend vakwerk.

Bij de beoordeling van een Strut-and-Tie model moeten trekstaven, drukstaven, dwarskrachten in drukdiagonalen en vergelijkbare elementen worden geanalyseerd. Voldoet het model niet, dan moet een nieuwe geometrie worden gekozen. In de praktijk kiest de constructeur echter vaak slechts één geometrie en beoordeelt vervolgens alleen de wapening, wat tot aanzienlijke fouten kan leiden.

Ter illustratie is in Fig. 2(b) een alternatief vakwerk weergegeven in stippellijnen. Voor de twee aangegeven staafwerkmodellen leidt het verschil in helling van de schuine strut tot een verschil van 30% in de dwarsbalkkracht. De keuze van een vakwerkmodel hangt altijd sterk af van ervaring. Bij complexere details is het kiezen van een staafwerkmodel dat het werkelijke gedrag van de constructie voldoende benadert vaak niet eenvoudig.

Bovendien is de vakwerkanalogie uitsluitend geschikt voor het ontwerp van de uiterste grenstoestanden (UGT). Ontwerpen voor bruikbaarheidsgrenstoestanden (BGT), zoals vervorming en scheurvorming, kritieke criteria in de bruggenbouw vanwege hun directe invloed op de levensduur van de constructie, zijn hiermee niet mogelijk.

Compatibele spanningsveldmethode - CSFM

De CSFM is een moderne, niet-lineaire methode voor de analyse van D-gebieden en elementen waarvan de werking kan worden vereenvoudigd tot een vlakspanningsprobleem, oftewel een 2D-model. Ze is echter nog steeds gebaseerd op fundamentele en veilige aannames uit de normen: beton draagt geen trek, en alle trekspanning moet worden overgebracht door de wapening.

De Compatible Stress Field Method (CSFM) is een evolutie van de vakwerkanalogie en compressieveldmethoden, waarbij de belangrijkste nadelen van deze methoden, zoals eerder beschreven—onzekerheid bij modelselectie, beperkte mogelijkheden tot automatisering en onvermogen om bruikbaarheidsgrenstoestanden te beoordelen—zijn weggewerkt.

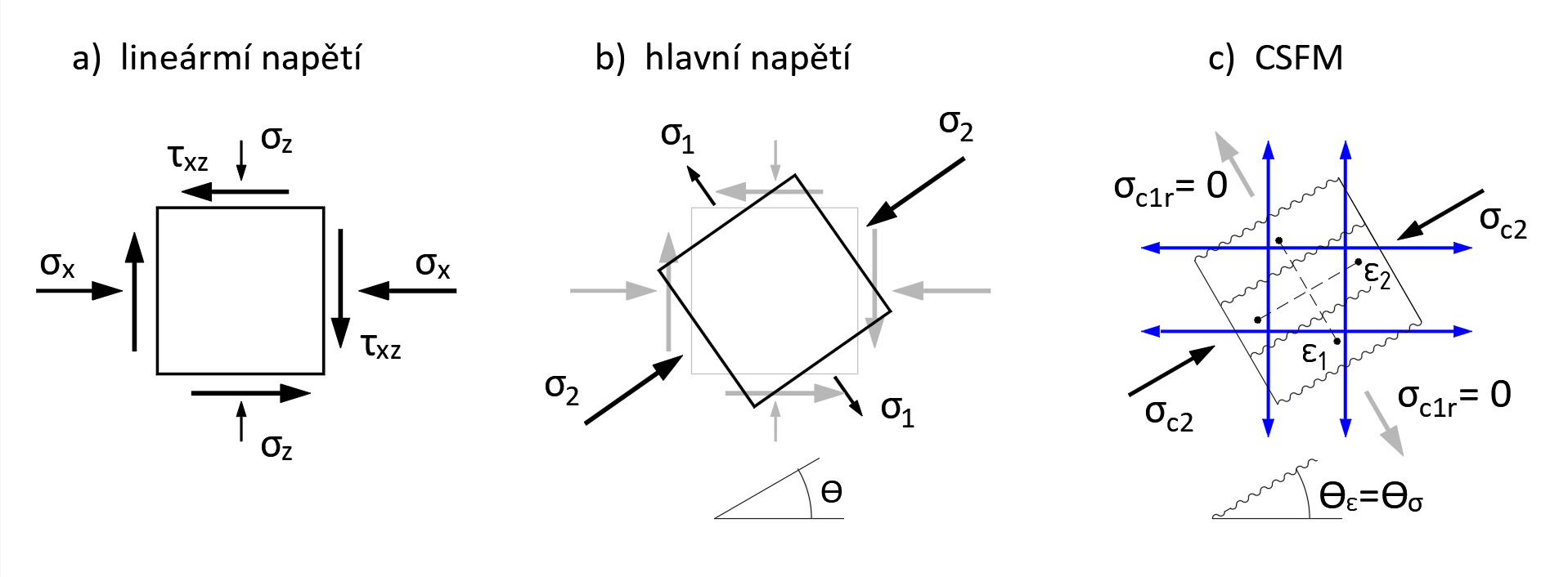
Het doel van dit artikel is de kern van de CSFM uit te leggen, ook al vereist dit gedeeltelijke vereenvoudigingen. Het principe van CSFM kan worden geïllustreerd aan de hand van de spanningen in een basis vlakke element van een gewapende betonconstructie. Fig. 3a toont de elementspanning zoals beschreven in standaard leerboeken over elasticiteit en sterkte. In ons voorbeeld betreft dit de spanning op één punt in de constructie, bijvoorbeeld verkregen via een lineaire elastische analyse met de eindige-elementenmethode (FEM).

Het element wordt belast met een horizontale spanning σx, een verticale spanning σy en een schuifspanning τxy. Uit deze spanningen kunnen de hoofdspanningen en hun hellingshoek θ worden bepaald (Fig. 3b). Het element wordt vervolgens geanalyseerd op basis van de hoofdtrekspanning σ1 en de hoofddrukspanning σ2.

Figuur 3. Principe van CSFM: a) lineaire, elastische spanning van het vlakke element; b) hoofdspanning; c) spanningen in de CSFM oplossing.

Hoe zien de spanningen van hetzelfde element eruit wanneer het wordt geanalyseerd met CSFM? Dit is weergegeven in Fig. 3c. In de richting van de hoofddrukspanningen σ2 draagt het samengedrukte beton bij en wordt een drukveld met spanning σc2 gevormd. Zoals eerder vermeld, is de basisaanname dat beton geen trek opneemt. Dwarse hoofdtrekspanningen σ1 worden daarom niet door het beton overgedragen, waardoor zich scheuren loodrecht op hun richting vormen. De spanning σc1r moet daarom nul zijn.

Om falen van het 2D-element te voorkomen, moeten alle trekspanningen door de wapening worden opgenomen (in blauw weergegeven in Fig. 3c). De wapening maakt deel uit van het rekenmodel. Wanneer deze spanningsanalyse met CSFM continu wordt uitgevoerd over het gehele 2D-gebied, ontstaat een continu druk- en trekspanningsveld in de wapening. Een vereenvoudigde grafische weergave van het CSFM-spanningsveld voor de kop van onze pijler is weergegeven in Fig. 7a. De figuur toont naast de benuttingsgraad van beton en wapening ook de variërende richtingen van de berekende drukspanningen σc2 in de verschillende regio’s.

De analyse van een detail of constructie met CSFM is gebaseerd op de eindige-elementenmethode. Beton wordt gemodelleerd met 2D-wandelementen en de wapening met 1D-elementen (Fig. 6). De analyse wordt niet in één stap uitgevoerd, omdat het een duidelijk niet-lineair probleem betreft (beton draagt geen trek). Belastingen worden stapsgewijs aangebracht, en het niet-lineaire stelsel van vergelijkingen wordt opgelost met de Newton-Raphson methode.

Tijdens de berekening ontstaan fictieve, uitgesmeerde scheuren (gemiddelde waarde ε1) loodrecht op de richting van de hoofdspanningen. Deze richtingen kunnen veranderen wanneer het element “progressief scheurt” in opeenvolgende belastingsstappen. Samengevat beschouwt CSFM een fictieve spanningsvrije, roterende scheur.

De FEM-oplossing met CSFM resulteert in een meegaand spanningsveld: het beton breekt niet in afzonderlijk werkende stutten, maar levert een continu veld van proportionele spanningen over het gehele 2D-domein. Dit is een groot voordeel ten opzichte van klassieke Strut-and-Tie benaderingen en maakt het mogelijk om het rekenmodel te automatiseren en verder te verfijnen, zoals in de volgende paragrafen wordt beschreven.

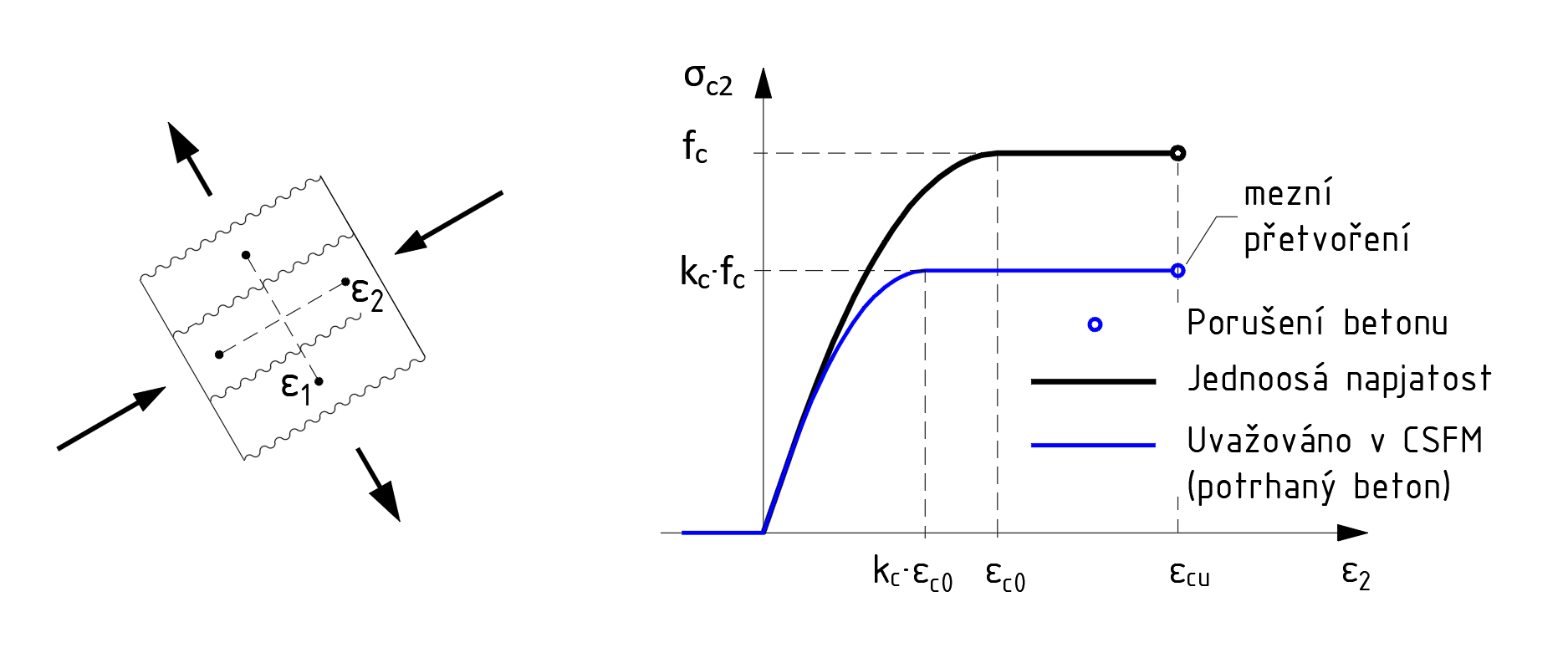
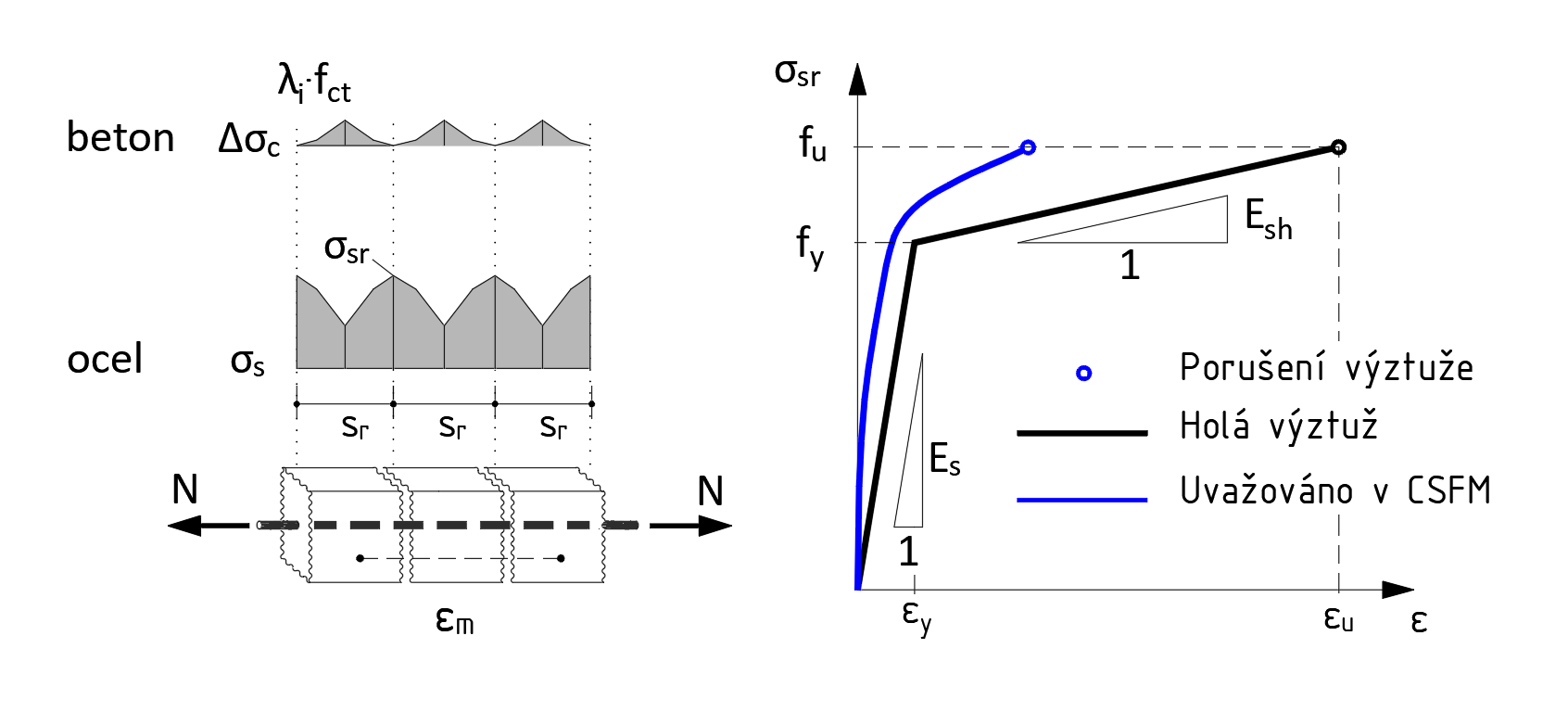
Fig. 4: Werkdiagram van beton, aangepast voor compression softening door dwarstrekspanningen (ε1 > 0 en ε2 < 0).

De eenvoudige formulering van CSFM maakt het mogelijk het standaard parabolisch-rechthoekige werkdiagram voor beton in druk toe te passen. Wanneer beton beschadigd raakt door trekscheuren, neemt de druksterkte af (Fig. 4). Dit Compression softening effect wordt meegenomen via de effectieve druksterkte, aangepast met reductiefactor kc op basis van de dwarstrekspanningen ε₁. Zo kan de effectieve druksterkte automatisch per doorsnede worden berekend.

Het Tension stiffening effect van het trekbeton tussen scheuren wordt ook meegenomen. De gemiddelde wapeningsrek ε_m wordt gebruikt om het werkdiagram van de wapening aan te passen (Fig. 5). Hierdoor wordt de stijfheid van een gescheurd gewapend betonelement realistisch weergegeven. Beton draagt nog steeds geen trek; de maximale spanning in de wapening σ_sr bepaalt de capaciteit (Fig. 5).

Fig. 5: Werkdiagram van de wapening en diagram rekening houdend met de gemiddelde relatieve wapeningsspanningen met het effect van trekwapening.

CSFM maakt gebruik van gebruikelijke eenassige materiaalmodellen zoals gedefinieerd in de ontwerpnormen. Voor de berekening van de uiterste grenstoestand wordt de gedeeltelijke betrouwbaarheidsfactormethode toegepast. De eenvoud van CSFM maakt de methode geschikt voor de engineeringpraktijk en consistent met de ontwerpnormen.

Hoewel het een niet-lineaire FE-analyse betreft, hoeft de constructeur geen aanvullende materiaaleigenschappen in te voeren die mogelijk nog niet beschikbaar zijn in het ontwerpstadium en normaal nodig zijn voor breukmechanica-gebaseerde FEA. Een groot voordeel van CSFM is dat, naast de uiterste grenstoestanden, ook bruikbaarheidsgrenstoestanden kunnen worden beoordeeld, zoals doorbuiging, spanningsbeperkingen en, in het bijzonder, scheurwijdte.

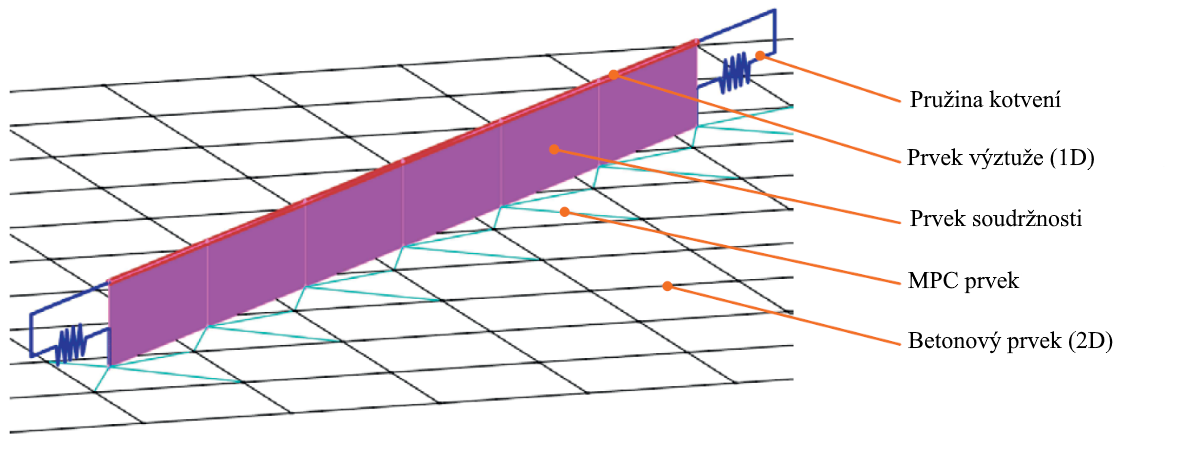
Fig 6. FEM-model: wapening eindige elementen verbonden met het betonnen elementennetwerk door MPC-links en eindige elementen.

Het FEM-model in CSFM bestaat uit verschillende typen eindige elementen (afbeelding 6):

• 1-D element met axiale stijfheid dat de wapening modelleert
• 2-D isoparametrisch element dat het beton modelleert
• Eindveren voor het wapeningsverankeringsmodel
• Speciaal 2-D element om de cohesie tussen wapening en beton te modelleren
• Stijve en interpolerende constraints (MPC) tussen cohesie-elementen en beton

Als de ontworpen wapening bros bezwijken van het element voorkomt, blijkt de CSFM zeer goede voorspellingen te geven van de respons en de uiteindelijke capaciteit van de constructie ondanks de eenvoud van de formulering. Met andere woorden, de methode is niet geschikt voor bijvoorbeeld het ontwerp van liggers zonder dwarskrachtwapening die mogelijk bros gedrag vertonen. Verificaties van de methode inclusief experimenten worden gegeven in [1]. Een meer gedetailleerde beschrijving van de methode valt buiten het bestek van dit artikel en is ook te vinden in [1].

Het is duidelijk dat de principes van CSFM algemeen zijn en dat de toepassing dus niet beperkt is tot D-gebieden, maar gebruikt kan worden om hele elementen of bijvoorbeeld prefab-onderdelen te modelleren en waarbij het element vereenvoudigd kan worden tot een vlak 2D-model. De methode en de implementatie ervan in software zijn ook uitgebreid met de mogelijkheid om voorgespannen en nagespannen wapening te specificeren.

Voorbeeld van een paalkopontwerp

Een praktische toepassing van de CSFM-methode wordt getoond in het brugpijlerhoofdontwerp in Fig. 1. Dit is de tweede pijler van een doorlopende brug met drie overspanningen van 30 m, 42 m en 30 m. De kop van de gewapend betonnen brugpijler is ontworpen in C40/50 beton en de dikte (in de lengterichting van de brug) is 2 m.

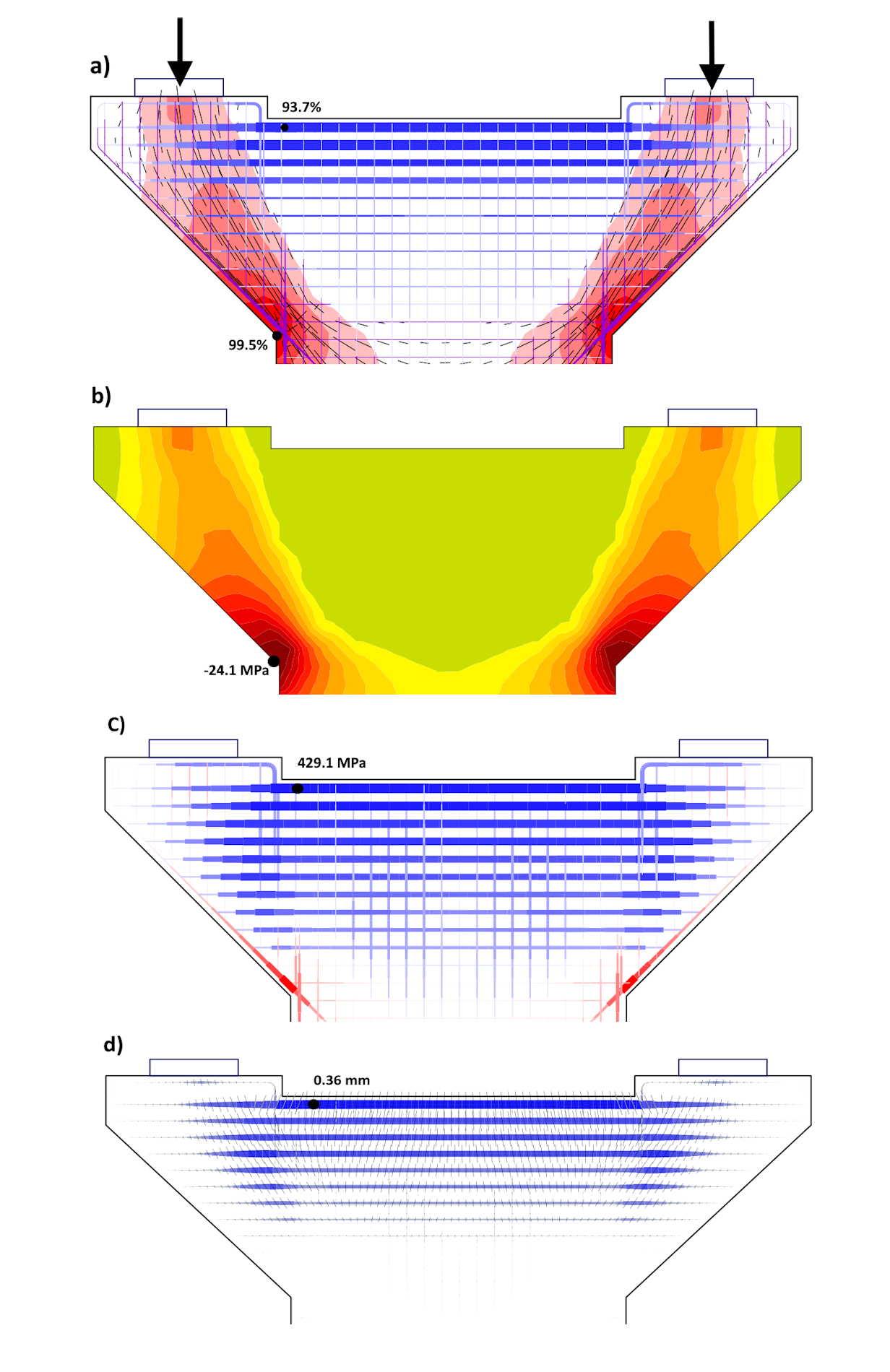
Fig. 7. Pijlerhoofd: a) beknopt ontwerp; b) spanningen in wapening; c) spanningen in beton, d) scheurwijdte.

Aan de bovenkant van de paalkop werd een dwarsbalk ontworpen met B500-wapening 20×ø28 + 20×ø25 (bovenste vier lagen). Fig. 7a toont een beknopt ontwerp bij de uiterste grenstoestand, met de drukspanningen in het beton, de richtingen van de drukspanningen en de spanningen in de wapening. Meer gedetailleerde spanningsverlopen in beton en wapening zijn weergegeven in Fig. 7b en 7c.

De spanning in de wapening ligt net onder de vloeigrens, en ook de spanningen in het beton blijven onder de ontwerpsterkte. De scheurwijdteberekening (Fig. 7d) laat echter zien dat het ontwerp niet voldoet aan de BGT: w_max = 0,36 mm > w_lim = 0,3 mm. Om aan de grenswaarde te voldoen, moet de wapening worden verhoogd tot 20×ø32 + 20×ø28. Bij een strengere limiet w_lim = 0,2 mm (bijvoorbeeld voor een pijler nabij een weg met zoutnevel, omgevingsinvloedniveau XF2) is zelfs 24×ø32 + 24×ø28 noodzakelijk.

Conclusie

CSFM is geschikt voor de engineeringpraktijk omdat het eenvoudige materiaalmodellen gebruikt die zijn gedefinieerd in de ontwerpnormen. De methode maakt bovendien het ontwerp van bruikbaarheidsgrenstoestanden naast uiterste grenstoestanden mogelijk, wat voorheen moeilijk was met bijvoorbeeld Strut-and-Tie modellen. Dankzij de implementatie van CSFM in IDEA StatiCa Detail kan de respons van de constructie realistisch worden vastgelegd, en kunnen discontinuïteitsgebieden en grotere samenstellingen efficiënt en veilig worden ontworpen en beoordeeld.

De ontwikkeling van CSFM is grotendeels gebaseerd op het werk van professor Walter Kaufmann, hoofd van de leerstoel Structural Engineering aan het Swiss Federal Institute of Technology (ETH) Zürich. Hij en zijn team hebben tevens de verificatie van de methode en de software-implementatie uitgevoerd.

Auteur

Dit artikel verscheen in Roads and Railways 01/2024

Ing. Pavel Kaláb, Ph.D.

IDEA StatiCa s.r.o.

Literatuur

[1] KAUFMANN, Walter, et al.: Compatible stress field design of structural concrete, ETH Zurich, 2020, ISBN 978-3-906916-95-8,

[2] KAUFMANN, W., MARTI, P.: Structural Concrete: Cracked Membrane Model. Journal of Structural Engineering 124 (12): 1467-75, 1998 https://doi.org/10.1061/(ASCE)0733-9445(1998)124:12(1467).

[3] KRAUS, M., WEBER, M., KAUFMANN, W., BOBEK, L.: Numerieke analyse van experimenteel geteste kozijnhoeken met openingsmomenten met behulp van de Compatible Stress Field Method (CSFM). In: Computational Modelling of Concrete and Concrete Structures, pp. 694-03. CRC Press, 2022 https://doi.org/10.1201/9781003316404