Boutkrachtverdeling in kopplaat liggerkolomverbinding

In dit artikel gaan we in op de verdeling van boutkrachten en de factoren die hier invloed op hebben. Het vaststellen van de werkelijke krachtsverdeling in een verbinding is vaak onmogelijk. Dit vraagt inzicht in het gedrag van de verbinding en kennis van de verschillende stijfheden en vervormingen. IDEA StatiCa Connection helpt deze effecten inzichtelijk te maken. We vergelijken de resultaten uit IDEA StatiCa met een handberekening voor een lineaire verdeling en laten zien waarom de werkelijke krachtsverdeling vrijwel altijd niet-lineair is.

Opzet 

We kunnen oneindig veel situaties bespreken, maar we zullen ons in dit voorbeeld beperken tot een ligger-kolom kopplaatverbinding met 2x5 M16 8.8 bouten en een puur buigend moment op de ligger. De lassen zijn als stompe lassen gemodelleerd en blijven buiten beschouwing.

In de volgende 5 punten bespreken we hoe verschillende factoren de boutkrachtverdeling beïnvloeden. 

1 - Vrij rotatiecentrum

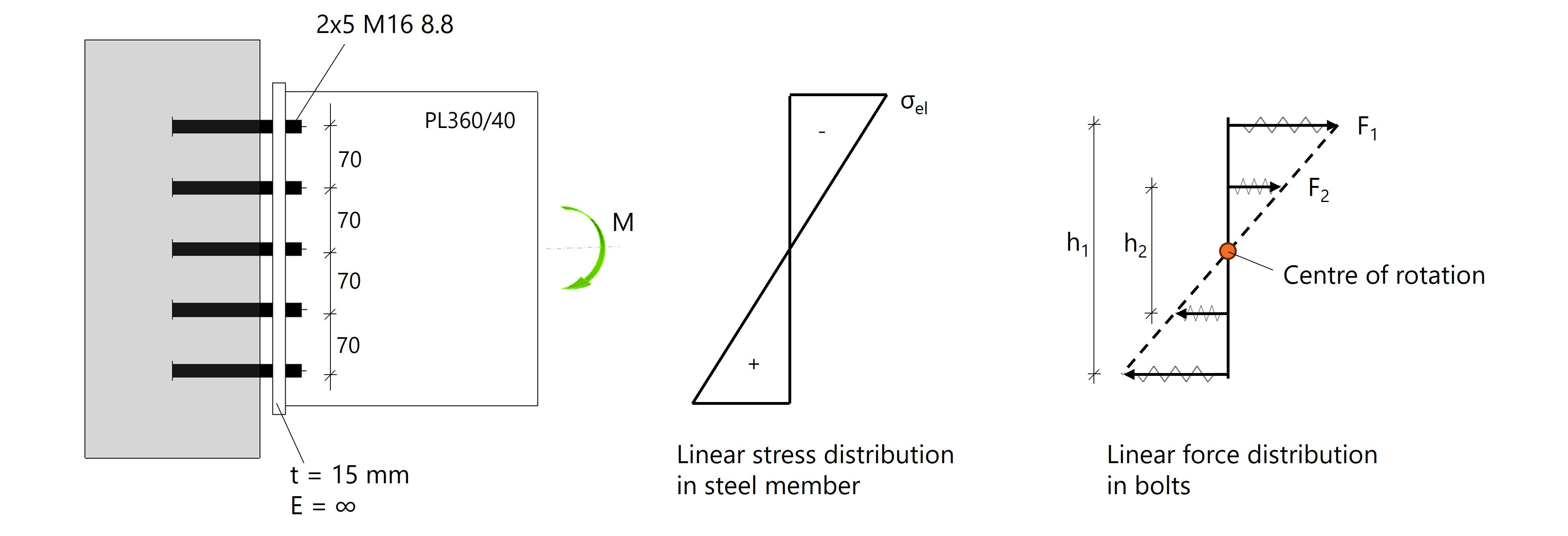
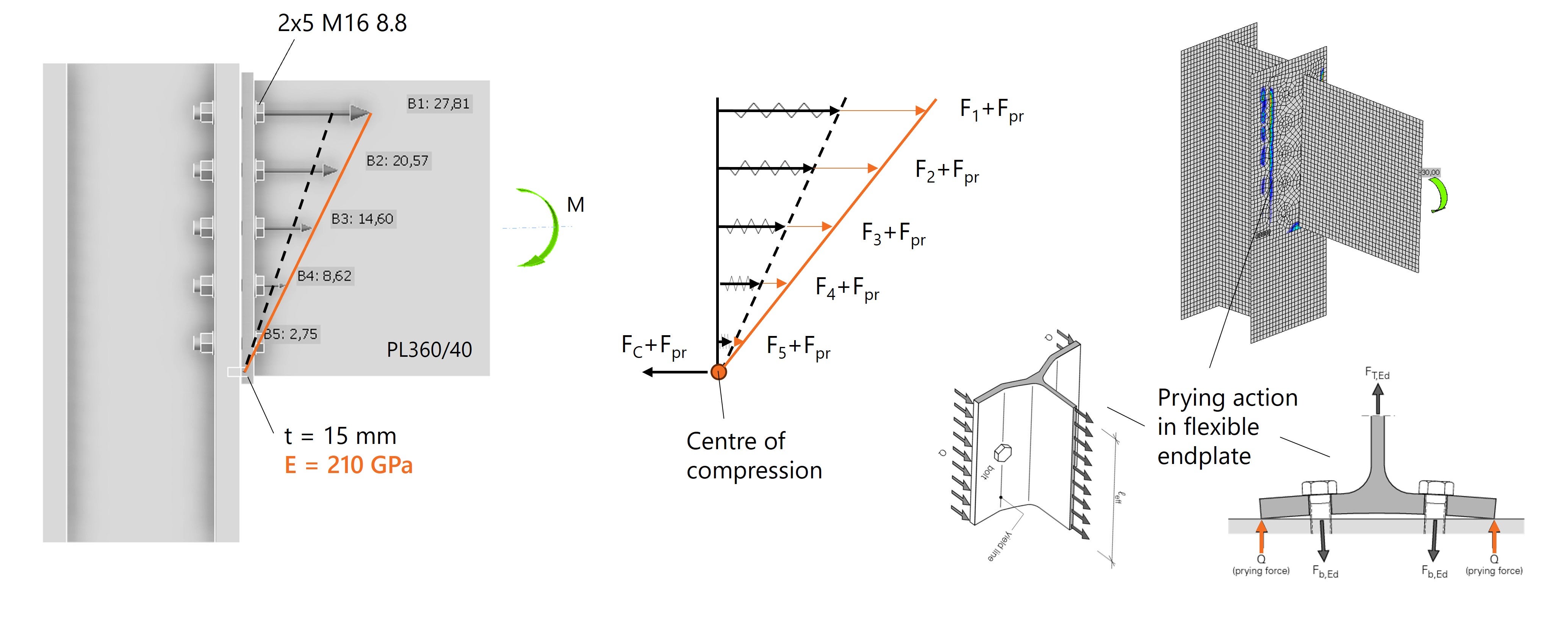
We beginnen met een theoretisch voorbeeld waarin de ligger als plaat PL360/40 wordt gemodelleerd. Door het buigend moment dat op de ligger werkt, ontstaat een lineair elastische spanningsverdeling, met de neutrale as exact in het midden. Deze spanningen vertalen zich naar een overeenkomstige verdeling van boutkrachten, maar alleen wanneer de stijfheden symmetrisch zijn, de bouten ook drukkrachten kunnen opnemen en het gedrag volledig elastisch blijft.

Om dit te benaderen hebben we in situatie 1 de verbinding gemodelleerd als een oneindig stijve voetplaat (E=∞) met ankers en een tussenruimte. De verbinding gedraagt zich hetzelfde in trek als in druk, waardoor er een ideaal rotatiepunt ontstaat ter hoogte van de middelste bout.

Fig. 1: Spanningsverdeling in ligger is gelijk aan de krachtsverdeling in de bouten door vrije rotatie.

De lineaire krachtsverdeling kunnen we controleren met een handberekening. Als F_i staat voor de kracht in één bout, dan krijgen we het volgende evenwicht:

\( M = 2F_1 \cdot h_1 + 2F_2 \cdot h_2 \)

Omdat de boutafstanden gelijk zijn krijgen we:

\( F_2 = \frac{1}{2} \cdot F_1 \)

Het buigend moment is in alle voorbeelden M = 30 kNm.

Als we dit invullen kunnen we F₁ en F₂ berekenen: 

\( M = 2F_1 \cdot h_1 + F_1 \cdot h_2 = 2F_1 \cdot 0.28 + F_1 \cdot 0.14 = 0.70 F_1 = 30 \) kNm

\( F_1 = 30 / 0.70 = 42.86 \) kN (per bout)

\( F_2 = F_1 / 2 = 42.86 / 2 = 21.43 \) kN (per bout)

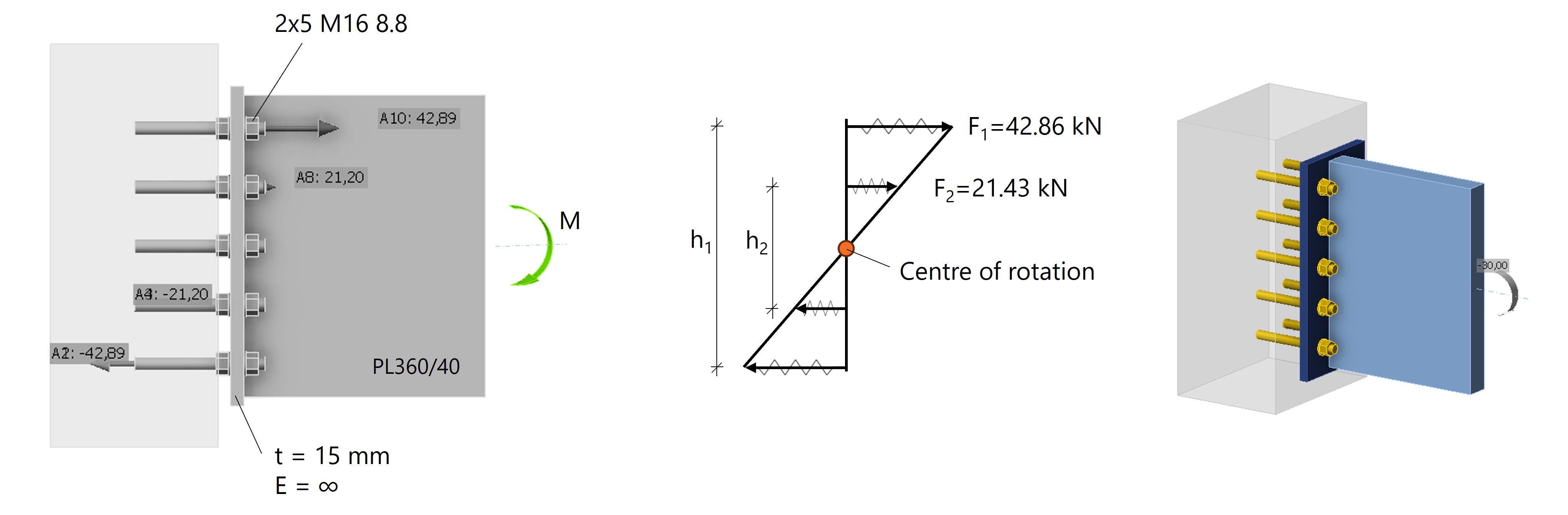
De resultaten voor F₁ en F₂ worden vergeleken met de berekende boutkrachten in IDEA StatiCa. Hieronder zien we dat de krachten in de bouten nagenoeg hetzelfde zijn.

Fig. 2: Lineaire boutkrachtverdeling in IDEA StatiCa door de bouten te modelleren als ankers met tussenruimte.

*Opmerking: Om de CBFEM berekening met de handberekening te kunnen vergelijken, moeten we uitgaan van een oneindig stijve kopplaat en de ligger modelleren als een plaat PL360/40 in plaats van een I-profiel. Later zullen we zien waarom dit belangrijk is.

2 - Gedwongen rotatiecentrum

In een werkelijke kopplaatverbinding nemen de bouten geen drukkrachten op en wordt de druk overgedragen via contact tussen de kopplaat en de kolomflens. Er is een verandering in stijfheden waardoor het rotatiecentrum, nu ook wel het drukpunt genoemd, naar beneden verschuift.

Om de handberekening goed te kunnen vergelijken hebben we onderaan de kopplaat een smalle strip gemodelleerd, zodat het drukcentrum altijd lokaal aan de onderzijde van de kopplaat ligt.

Daarnaast is de ligger gemodelleerd als plaat en hebben we de E-modulus van de staalonderdelen verhoogd om de vervormingen te beperken. Zo ontstaat een perfect lineaire verdeling van de boutkrachten met het rotatiepunt onderaan de kopplaat.

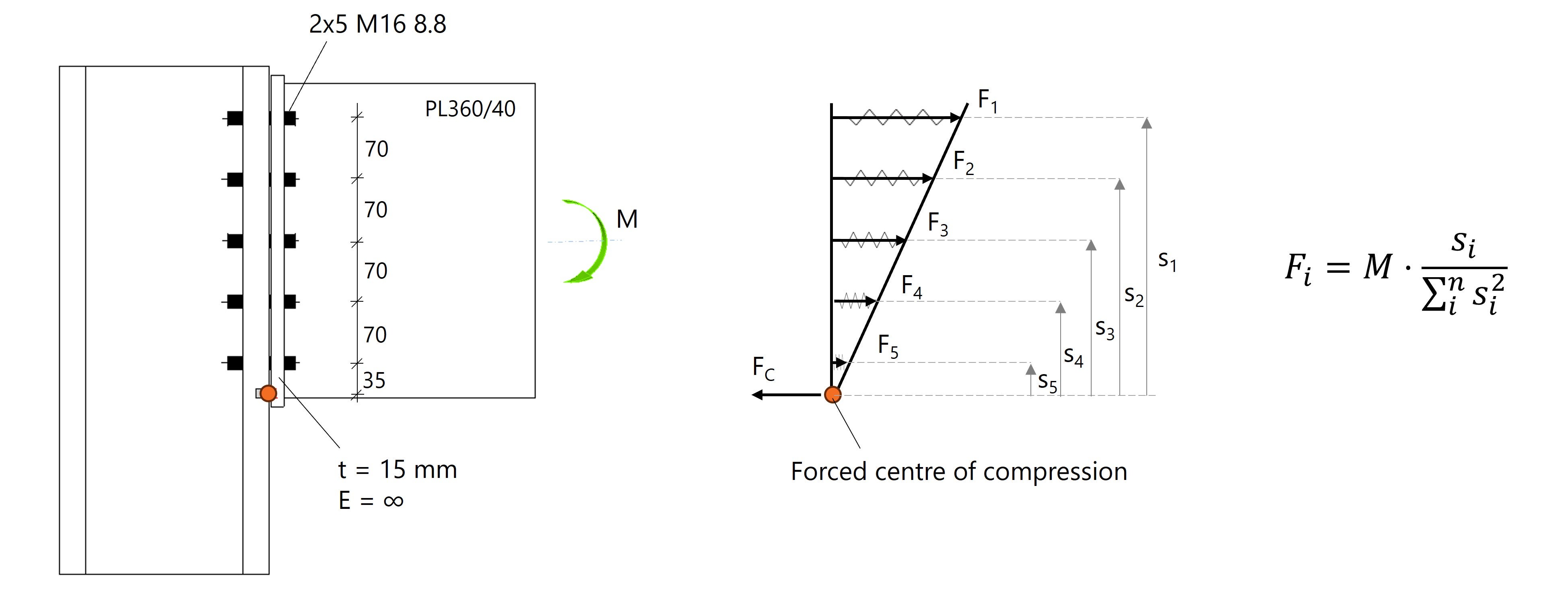
Fig. 3: Lineaire boutkrachtverdeling met het rotatiecentrum onderaan de kopplaat als drukpunt.

Op basis van de bekende afstanden en belasting worden de boutkrachten berekend met de volgende vergelijking:

            \( F_i = M \cdot \frac{s_i}{\sum_{i}^{n} s_i^{2}} \)

Elke boutrij heeft 2 bouten en we gaan er vanuit dat de krachten gelijk zijn. Voor boutrij 1 krijgen we:

\( 2F_1 = M \cdot \frac{s_1}{\sum_{i}^{n} s_i^{2}} = 30 \cdot \frac{0.315}{(0.315^2+0.245^2+0.175^2+0.105^2+0.035^2)} \) = 46.75 kN

Dat geeft \( F_1 = 46.75/2 = 23.37 \) kN 

Op deze manier kunnen we per rij de kracht van één bout uitrekenen:

• \(F_1\) = 23.37 kN
• \(F_2\) = 18.18 kN
• \(F_3\) = 12.98 kN
• \(F_4\) = 7.79 kN
• \(F_5\) = 2.59 kN

De kracht in het drukpunt bedraagt:

\( F_C = F_1 + F_2 + F_3 + F_4 + F_5 = 23.37 + 18.18 + 12.98 + 7.79 + 2.59 = 64.91 \)  kN

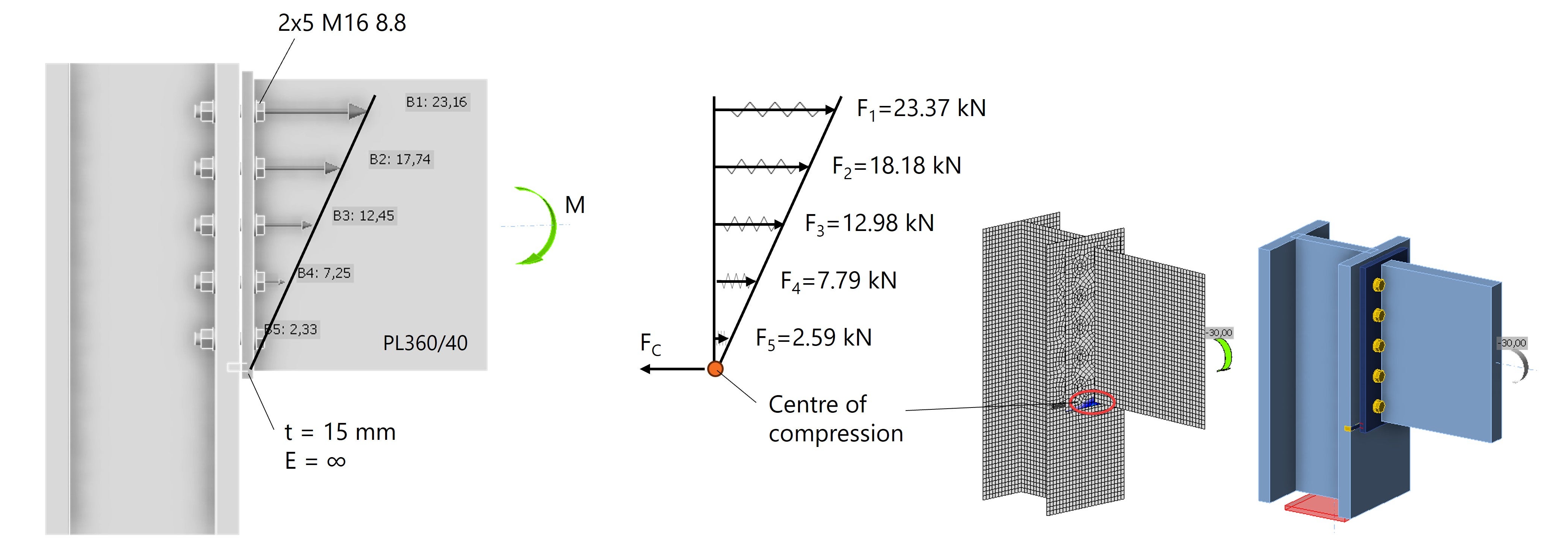
De berekende krachten F₁ t/m F₅ komen goed overeen met de boutkrachten in IDEA StatiCa, zie Fig. 4.

Fig. 4: Lineaire boutkrachtverdeling in IDEA StatiCa met het drukpunt onderaan de kopplaat.

De handberekening kan goed worden vergeleken met de CBFEM‑berekening in IDEA StatiCa. Dit is echter alleen mogelijk omdat we uitgaan van een onrealistisch stijve kopplaat en een geforceerd rotatiecentrum. Laten we de kopplaat nu modelleren met de werkelijke elasticiteitsmodulus E=210 GPa.

3 - Flexibele kopplaat

We nemen hetzelfde voorbeeld als in situatie 2, maar nu is de kopplaat uitgevoerd in staal S235 met E=210 GPa. De verdeling blijft lineair, maar de boutkrachten nemen in waarde toe, en zijn niet meer direct te vergelijken met onze handberekening. Wat is hier aan de hand?

Door de resultaten in IDEA StatiCa nauwkeurig te analyseren zien we vervormingen in de kopplaat en treedt hefboomwerking (prying action) op. De trekkracht veroorzaakt doorbuiging van de kopplaat, waardoor extra drukspanningen aan de zijkanten ontstaan die de boutkrachten laten toenemen. Dit hefboomseffect is goed zichtbaar in IDEA StatiCa door het weergeven van de contactspanningen tussen de kopplaat en de kolomflens, zie Fig. 5.

Fig. 5: Boutkrachten nemen toe ten gevolgen van het hefboomseffect (wrikkrachten).

In IDEA StatiCa worden wrikkrachten automatisch meegenomen in de EEM-berekening en worden alle bouten daarop getoetst. Het narekenen met de hand is mogelijk maar vergt meer tijd.

Tot nu toe hebben we de ligger gemodelleerd als plaat PL360/40, om een zo voorspelbaar mogelijke krachtsverdeling te kunnen analyseren. Maar wat als de ligger een IPE360 is?

4 - Wat als de ligger een I-profiel is?

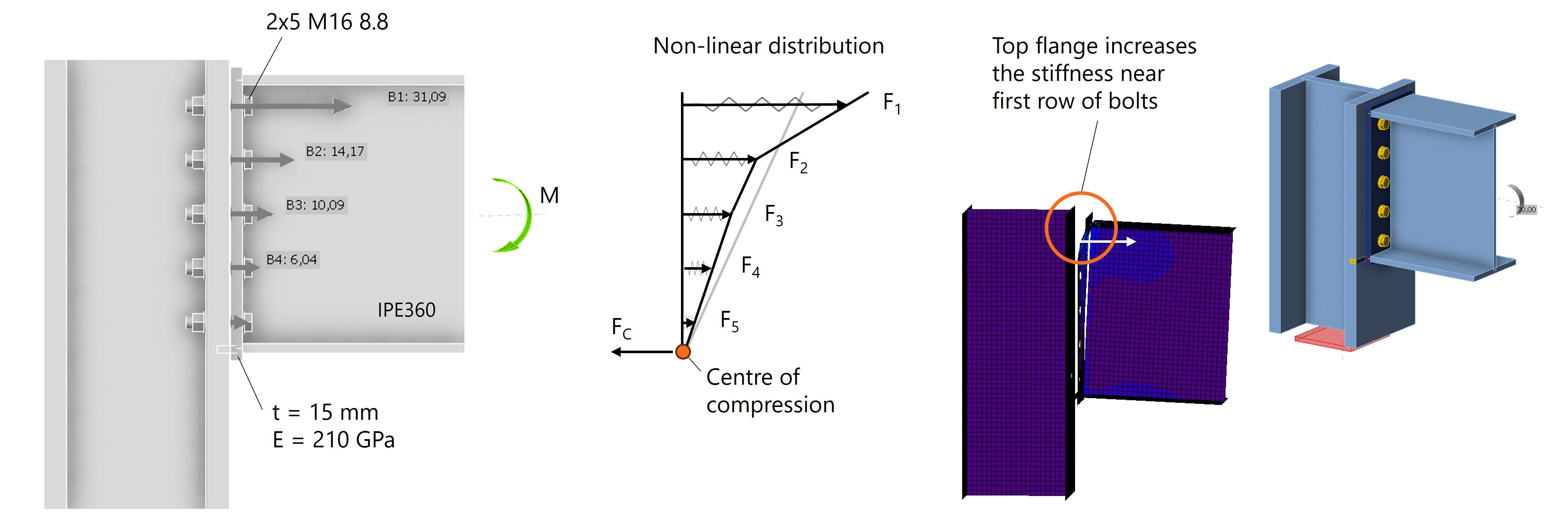
Wanneer we de ligger modelleren als een I-profiel, wat in de praktijk gebruikelijker is, verandert de relatieve stijfheid in de verbinding. Door de aanwezigheid van een bovenflens neemt de stijfheid rondom de bovenste boutrij toe. En wat gebeurt er wanneer de stijfheid toeneemt? De stijvere delen nemen meer kracht op, waardoor de boutkrachten in de bovenste rij hoger worden.

Het resultaat is een niet-lineaire verdeling van de boutkrachten, zoals weergegeven in Fig. 6.

Fig. 6: Niet-lineaire boutkracht verdeling door een verandering van stijfheidsverhoudingen.

Bij het verdelen van de krachten over een verbinding moet rekening worden gehouden met de stijfheidsverhoudingen binnen de verbinding. Dit is het moeilijkste onderdeel van het berekeningsprocess, omdat oneindig veel factoren invloed kunnen hebben. Denk bijvoorbeeld aan:

• Dikte kopplaat
• Type doorsnede
• Verstijvers
• Boutpatroon
• Materiaalkwaliteit
• Elastisch of plastisch gedrag

Door de resultaten in IDEA StatiCa nauwkeurig te analyseren, krijgen we inzicht in de krachtverdeling en kunnen we ons ontwerp eventueel optimaliseren.

5 - Plaats bouten waar ze het meest bijdragen

Tot slot wordt laten zien hoe de krachtsverdeling kan worden beïnvloed door het verplaatsen van de bouten, met als doel een zo effectief mogelijk ontwerp te creëren.

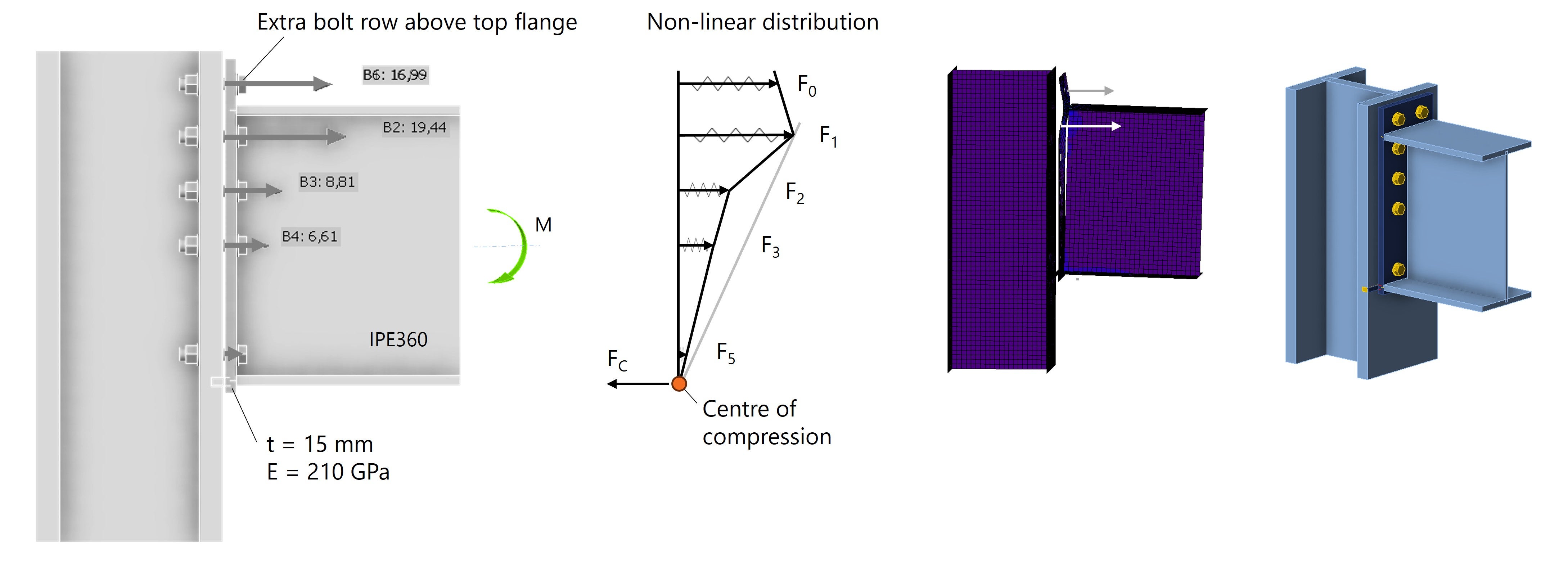
Als we aannemen dat er alleen een neerwaarts buigend moment aanwezig is, dan is de meest effectieve plaats voor de bouten vlak bij de bovenflens. Deze locatie ligt het verst van het rotatiecentrum en bevindt zich in het stijfste gedeelte, vlak bij de flenzen. Door de kopplaat te verlengen en boutrij 4 te verplaatsen naar boven de bovenflens, worden de krachten verlaagd en beter verdeeld over de bouten in de bovenste twee rijen, zie Fig. 7.

Fig. 7: De bouten nabij de bovenflens nemen de meeste kracht op.

Het gedeelte boven de bovenflens is slapper dan onder de bovenflens waardoor de bouten in rij 0 een iets kleinere kracht opnemen. We zouden dit nog verder kunnen optimaliseren door aan de bovenkant een verstijver toe te voegen, zie Fig. 8.

Conclusie

De boutkrachtverdeling in een kopplaat is in de praktijk nooit volledig lineair. Verschillen in stijfheden, vervormingen en hefboomwerking zorgen voor een complex krachtenverloop, waardoor handberekeningen slechts een vereenvoudigde benadering bieden. 

Met IDEA StatiCa kunnen we het realistische gedrag analyseren. We zien hoe krachten zich verdelen en welke invloed factoren zoals kopplaatdikte, profieltype, materiaalstijfheid en boutpositie hebben. Dit inzicht maakt het mogelijk om verder te gaan dan alleen toetsen. Verbindingen kunnen doelgericht worden geoptimaliseerd, bijvoorbeeld door bouten strategisch te plaatsen of aanvullende verstijvers toe te voegen.

Slotopmerking

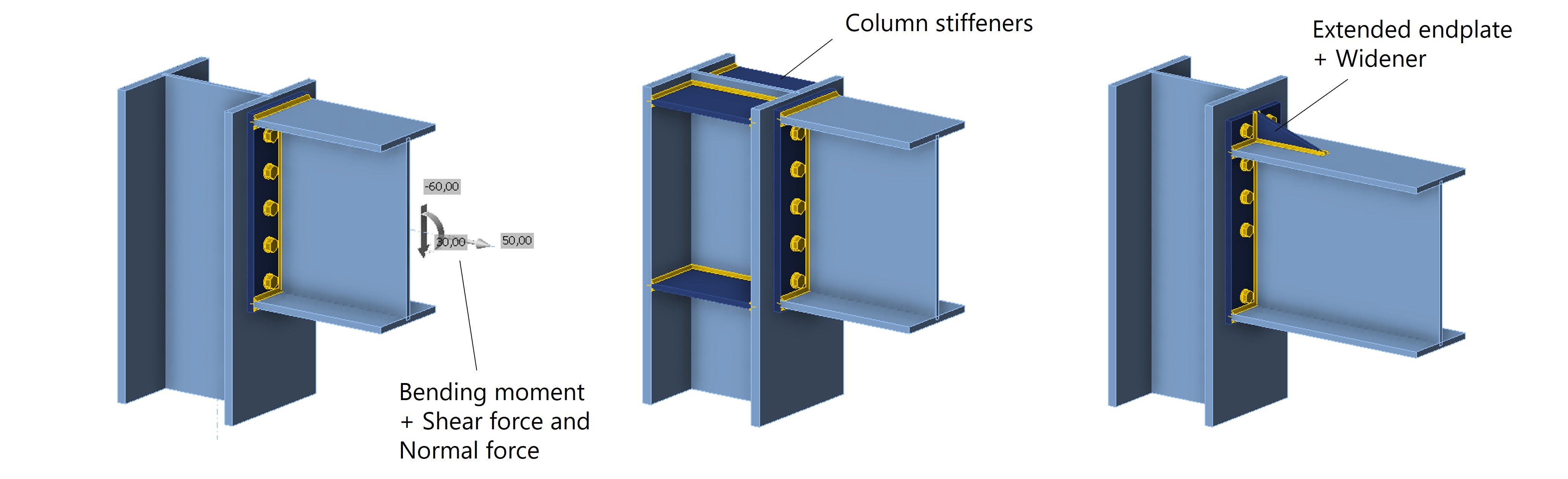
Dit onderzoek heeft zich beperkt tot een kolom-liggerverbinding met kopplaat onder buigend moment. Men kan zich voorstellen dat de boutkrachtverdeling nog complexer wordt wanneer er ook een dwarskracht of normaalkracht wordt toegepast, andere profieldoorsnedes worden gebruikt, verstijvers worden toegevoegd, enzovoort. Al deze factoren beïnvloeden het krachtenverloop door de stijfheid van de verschillende onderdelen te veranderen. 

Fig. 8: Kopplaat verbinding met andere interne krachten - kolomverstijvers - verlengde kopplaat met versteviging.