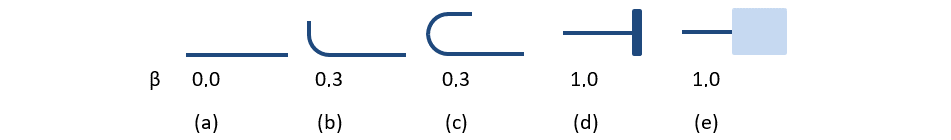Las distintas verificaciones exigidas por la norma ACI 318-19 se evalúan a partir de los resultados directos proporcionados por el modelo. Las verificaciones se llevan a cabo para la resistencia del hormigón, la resistencia de la armadura y el anclaje (esfuerzos cortantes de adherencia).
La resistencia del hormigón en compresión se evalúa como la relación entre la tensión principal equivalente máxima fc,eq (también σc,eq en el texto anterior) obtenida a partir del análisis de EF y el valor límite f'c,lim.
La tensión principal equivalente expresa la tensión uniaxial equivalente para un estado de tensión triaxial general.
\[f_{c,eq} = \sigma_{c3}} - \sigma_{c1}\].
El valor de fc, eq puede, por tanto, compararse directamente con los límites de resistencia uniaxial. Esta expresión se deriva de la aplicación de la teoría de la plasticidad de Mohr-Coulomb, asumiendo de forma conservadora el ángulo de fricción interna φ = 0°.
La resistencia de la armadura se evalúa tanto en tracción como en compresión como la relación entre la tensión en la armadura en las fisuras fs y el valor límite especificado fy,lim.
\[f_{y,lim} = \phi_{s} \cdot f_{y}\]
El esfuerzo cortante de adherencia se evalúa independientemente como la relación entre el esfuerzo de adherencia τb calculado mediante el análisis de EF y la resistencia de adherencia fbu.
Aunque la resistencia de adherencia no se define explícitamente en ACI 318-19, el cálculo de la longitud de desarrollo se puede encontrar en la Sección 25.4.2. Sin embargo, dado que la resistencia de adherencia es el dato básico para determinar la longitud de desarrollo, véase R25.4.1.1 y ACI Comité 408 1966, la resistencia de adherencia puede calcularse como sigue:
Supongamos que si anclamos la barra de armadura en un bloque de hormigón hasta la longitud de desarrollo ld o mayor, el arrancamiento de la armadura producirá la rotura de la armadura y no el arrancamiento del hormigón. Esto se puede escribir con la siguiente fórmula.
\[\pi\cdot d_{b} \cdot l_{d} \cdot f_{bu}=f_{y}\cdot A_{s}]
donde:
db es el diámetro de la barra de armadura, ld es la longitud de desarrollo, fbu es el límite de adherencia, fy es el límite elástico de la armadura yAs es el área de la barra de armadura.
De lo anterior se deduce fácilmente la fórmula para calcular la fuerza de adherencia:
\f_{bu}=frac{f_{y}\cdot A_{s}}{pi\cdot d_{b} \cdot l_{d} }].
La longitud de desarrollo ld se determina entonces de acuerdo con ACI 318-19 Tabla 25.4.2.3 de la siguiente manera:
\[l_{d}=\left( \frac{f_{y}\cdot\psi_{t}\cdot\psi_{e}\cdot\psi_{g}}{C\cdot\lambda\sqrt{f'_{c}}} \d_{b}]
donde:
C = 25 (2,1 para métrica) para no. 6 y barras más pequeñas y alambres deformados, C = 20 (1,7 para el sistema métrico) para no. 7 y barras mayores, λ = 1,0 para hormigón de peso normal, ψt, ψe, ψg se determinan de acuerdo con ACI 318-19 Tabla 25.4.2.3.
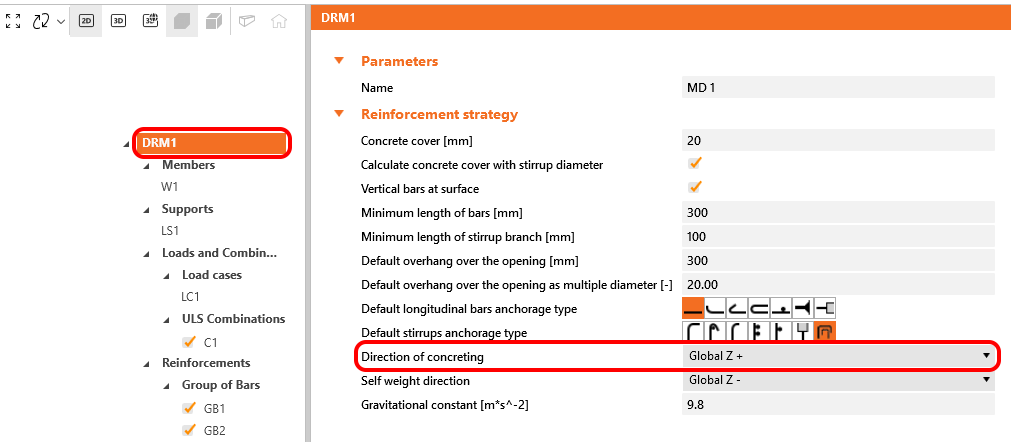
Sólo se soportan las armaduras no revestidas o revestidas de zinc (galvanizadas), por lo que ψe = 1,0. ψg se determina automáticamente a partir del grado de la armadura, y ψt se deriva automáticamente de la posición de la armadura en el modelo y de la dirección de hormigonado que puede establecerse en la aplicación para cada elemento del proyecto de la siguiente manera.
\[ \textsf{\textit{footnotesize{Fig. 46\qquadirección del hormigonado}}}]
Estas comprobaciones se realizan con respecto a los valores límite apropiados para las respectivas partes de la estructura (es decir, a pesar de tener una única calidad tanto para el hormigón como para el material de la armadura, los diagramas tensión-deformación finales diferirán en cada parte de la estructura debido a los efectos de rigidización por tracción y ablandamiento por compresión).
Fuerza total Ftot y fuerza límite Flim
La fuerza total Ftot es el resultado del análisis de elementos finitos y puede definirse de dos maneras.
\[F_{tot}=A_{s} \cdot f_{s}\]
dondeAs es el área de la barra de refuerzo y fs es la tensión en la barra.
O como suma de la fuerza de anclajeFa y la fuerza de adherencia Fbond.
\[F_{tot}=F_{a}+F_{bond}\]
dondeFa es la fuerza real en el muelle de anclaje y Fbond es la fuerza de adherencia que puede obtenerse integrando la tensión de adherencia τb a lo largo de la longitud de la barra de armadura l.
\[F_{bond}=C_{s} \cdot \int_{0}^{l}\tau_{b}\left( x \right)dx\]
Cs es la circunferencia de la barra de refuerzo.
La fuerza límiteFlim es la fuerza máxima en el elemento de la barra de refuerzo teniendo en cuenta la resistencia de la barra de refuerzo y también las condiciones de anclaje (unión entre el hormigón y la armadura y ganchos de anclaje, bucles, etc.).
\[F_{lim}=min_left( F_{lim,bond}+F_{au},F_{u} \right)\}]
\[F_{u}=f_{y,lim}\cdot A_{s}]
\F_{au}=f_{y,lim}dot A_{s}]
\F_{lim,bond}=C_{s}{cdot l}{cdot f_{bu}{]
donde Cs es la circunferencia de la barra de refuerzo, y l es la longitud desde el comienzo de la barra de refuerzo hasta el punto de interés.
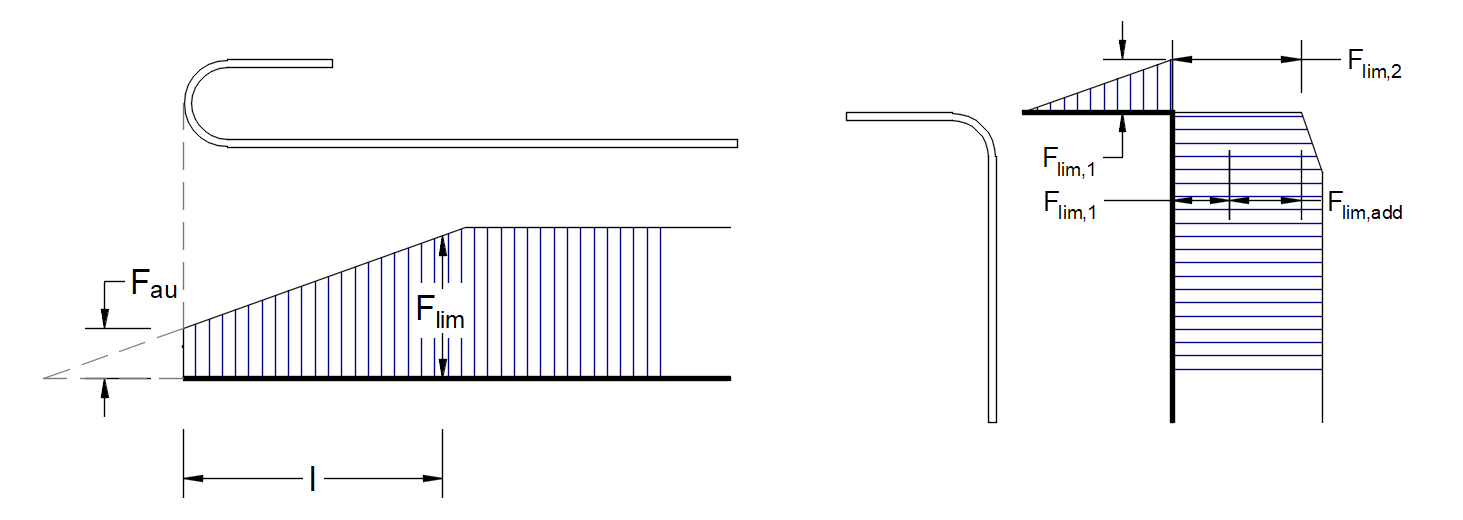
\[ \textsf{\textit{footnotesize{Fig. 47\qquad Definición de la fuerza límite Flim}}]
\[F_{lim,2}=F_{lim,1}+F_{lim,add}\]
dondeFlim,add es la fuerza adicional calculada a partir de la magnitud del ángulo entre elementos vecinos.Flim,2 debe ser siempre inferior aFu.
Los tipos de anclaje disponibles en CSFM incluyen una barra recta (es decir, sin reducción del extremo del anclaje), gancho de 90 grados, gancho de 180 grados, unión perfecta y barra continua. Todos estos tipos, junto con los respectivos coeficientes de anclaje β, se muestran en la Fig. 48 para la armadura longitudinal. Los valores de los coeficientes de anclaje adoptados se derivan de la comparación de la ecuación de la sección ACI 318-19 25.4.3.1 y ecuaciones tomadas de la sección ACI 318-19 25.4.2.3. Cabe señalar que, a pesar de las diferentes opciones disponibles, el CSFM distingue tres tipos de extremos de anclaje: (i) ninguna reducción de la longitud de anclaje, (ii) una reducción del 30% de la longitud de anclaje en el caso de un anclaje normalizado, y (iii) unión perfecta.
\[ \textsf{\textit{footnotesize{Fig. 48\qquad Tipos de anclaje disponibles y coeficientes de anclaje respectivos para barras de refuerzo longitudinal en CSFM:}}]
\(a) barra recta; (b) gancho de 90 grados; (c) gancho de 180 grados; (d) unión perfecta; (e) barra continua}}].
El coeficiente de anclaje de los estribos es siempre - β = 1,0.
Para cumplir con ACI, el resorte de anclaje debe ser utilizado en el cálculo, el resorte de anclaje es modificado por el coeficiente β por lo que el usuario debe utilizar uno de los tipos de anclaje disponibles al definir las condiciones de inicio y final de la armadura.