Muros cortantes con aberturas (ACI)

En este capítulo se examina el comportamiento de cuatro especímenes de muros de cortante de hormigón armado (CR) con aberturas. Su capacidad de carga lateral y ángulo de deriva (desplazamiento/longitud) se evaluaron utilizando el software IDEA StatiCa y se compararon con los datos experimentales reportados por Taleb et al. (2012).

Los resultados también se compararon con las capacidades de diseño calculadas utilizando el modelo de puntal y tirante (STM) incluido en ACI 318-19 (2019). Una de las probetas de muro de cortante ensayadas se seleccionó como modelo de referencia para su posterior análisis mediante el software ABAQUS (2023), donde se calcularon el ángulo de deriva, la distribución de tensiones principales y los patrones de fisuración, y se compararon con los medidos durante los experimentos. Además, se aplicó el modelo de confinamiento de Mander et al. (1988) para examinar en detalle el efecto del hormigón confinado en las capacidades del muro de cortante.

Estudio experimental

Para evaluar el comportamiento estructural de los muros de corte con aberturas, se estudiaron cuatro especímenes de muros estructurales RC de un solo vano, identificados como N1, S1, M1 y L1. Estos especímenes fueron construidos y probados por Taleb et al. (2012) en el laboratorio estructural de la Universidad de Kyoto bajo carga cíclica lateral invertida. Los muros se escalaron al 40%, representando los tres pisos inferiores de un edificio RC de seis pisos. Los principales objetivos de estos experimentos eran analizar el comportamiento lateral y comprender los efectos de los diferentes tamaños y ubicaciones de las aberturas en la distribución de las grietas y la resistencia al corte de los muros estructurales de CR. Se mantuvo la consistencia en el refuerzo primario en todos los especímenes, con variaciones en los ratios de apertura. Entre estas muestras, se seleccionó la L1 como modelo de referencia para su posterior análisis mediante el software ABAQUS.

Montaje experimental

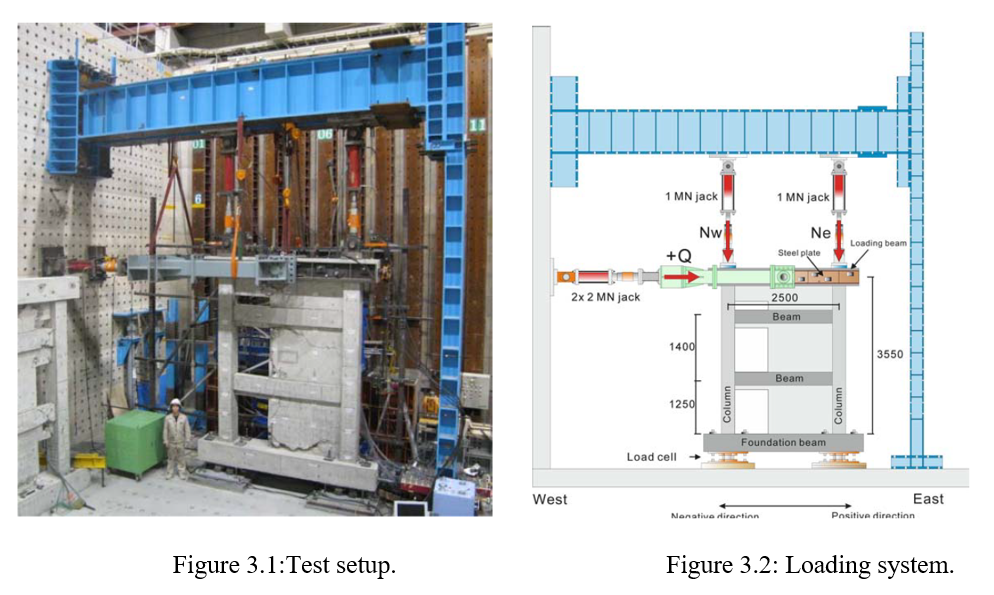
El montaje experimental y los detalles del sistema de carga se muestran en las Figuras 3.1 y 3.2, respectivamente. La carga lateral Q, fue aplicada a la viga de carga usando dos gatos hidráulicos de 2 MN (449.6 kips), entregando cargas cíclicas horizontales invertidas a los especímenes. Estas cargas se aplicaron en ambas direcciones, simulando las condiciones sísmicas del mundo real. Además de las cargas horizontales, se aplicaron cargas axiales verticales a las columnas utilizando dos gatos hidráulicos de 1 MN (224,8 kips), replicando las cargas en los tres pisos inferiores de un edificio de CR de seis pisos. Los niveles de carga vertical se eligieron para reflejar las cargas axiales a largo plazo esperadas en una estructura de este tipo, con cada gato aplicando inicialmente una carga de 400 kN (89,9 kips) para representar el peso de los pisos superiores.

Los dos gatos hidráulicos verticales se ajustaron para aplicar fuerzas axiales, Nw y_Ne, que variaban con la carga lateral Q, para mantener una relación de luz de corte(M/Ql) de 1,0. Aquí, M representa el momento en el vano de la estructura. Aquí, M representa el momento en la base del muro, Q es la carga horizontal y l es la distancia entre los centros de las columnas laterales. Esta configuración garantiza que el fallo por cortante se produzca antes de que se produzca la flexión del muro.

El impacto de la carga axial en la capacidad de corte fue mínimo ya que las columnas laterales permanecieron intactas hasta la conclusión de las pruebas.

Figura 3.1, 3.2 Montaje de la prueba, Sistema de carga

Muestras de ensayo

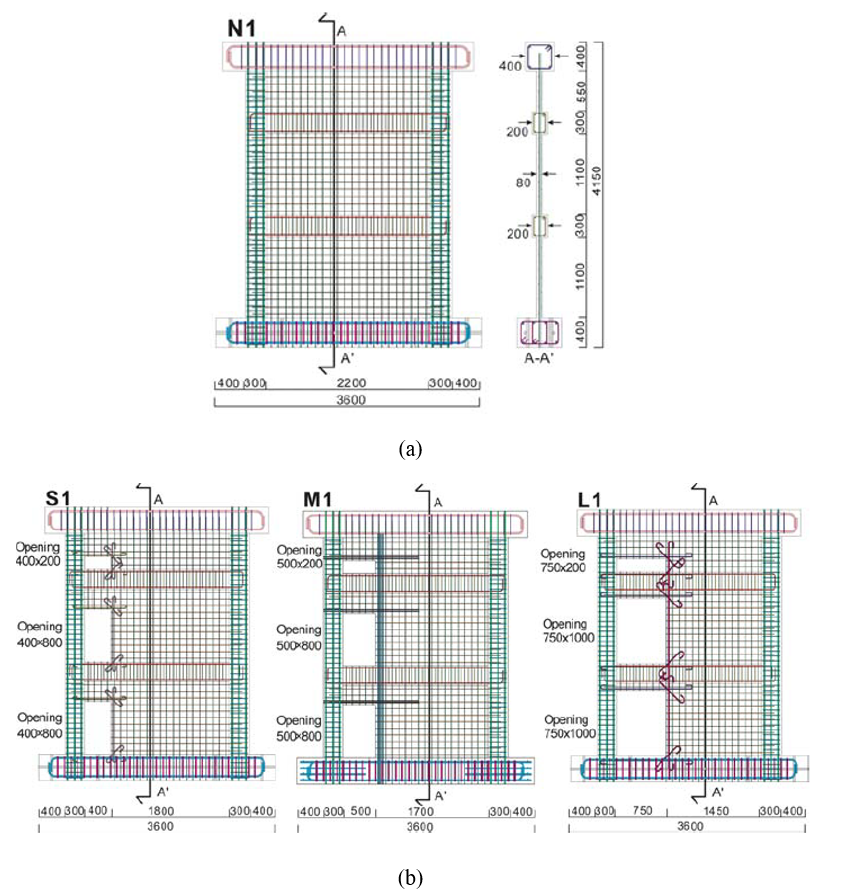
En la Universidad de Kioto se construyeron y ensayaron cuatro probetas de muro de hormigón armado. Como se muestra en la figura 3.3, tres especímenes (S1, M1, L1) tenían aberturas excéntricas, mientras que un espécimen (N1) no tenía aberturas. Las variables principales de las muestras de tres pisos con aberturas eran la proporción de apertura y la ubicación de las aberturas. Uno de los principales objetivos de las pruebas experimentales era evaluar el impacto de las diferentes relaciones de apertura en la resistencia a cortante de los muros estructurales. Los coeficientes de apertura para las muestras S1, M1 y L1 fueron de 0,30, 0,34 y 0,46, respectivamente.

Figura 3.3: Configuraciones de los especímenes y disposición de las barras de refuerzo: a) detalles y dimensiones del espécimen N1 sin abertura, y b) detalles de las dimensiones y aberturas de los especímenes S1, M1 y L1.

Análisis IDEA StatiCa

El comportamiento de las probetas de muro de cortante de hormigón armado con aberturas, tal y como se exploró en la Sección 3.3.1, se analizó utilizando el IDEA StatiCa Detail. Este estudio amplía la investigación previa de Taleb et al. (2012) y se centra en los especímenes N1, S1, M1 y L1. Estos especímenes se eligieron específicamente para investigar la influencia de las diferentes relaciones de apertura y ubicaciones en su rendimiento estructural. La metodología de modelado en IDEA StatiCa Detail integró la resistencia a compresión real del hormigón y los límites elásticos y últimos de las barras de acero de refuerzo, siguiendo los parámetros descritos por Taleb et al. (2012).

En el análisis IDEA StatiCa, se utilizaron factores de carga de 1,0 para ambos patrones de carga -el peso propio y la carga lateral aplicada- centrados en la combinación de carga del estado límite último (ULS). Para garantizar la exactitud de las simulaciones y su alineación con los resultados experimentales, los factores de material para el hormigón (_fc) y el acero de refuerzo (_fs) dentro de IDEA StatiCa se fijaron en 1,0.

El proceso de cálculo de la capacidad para IDEA StatiCa consistió en aumentar progresivamente la carga lateral aplicada en el centro de la viga superior hasta alcanzar cualquiera de las siguientes condiciones:

1. El hormigón en cualquier punto del modelo alcanzaba el 100% de su capacidad resistente bajo la carga aplicada.
2. El acero de refuerzo alcanza el 100% de su capacidad de resistencia bajo la carga aplicada.
3. El acero de anclaje alcanzó el 100% de su capacidad de resistencia bajo la carga aplicada.

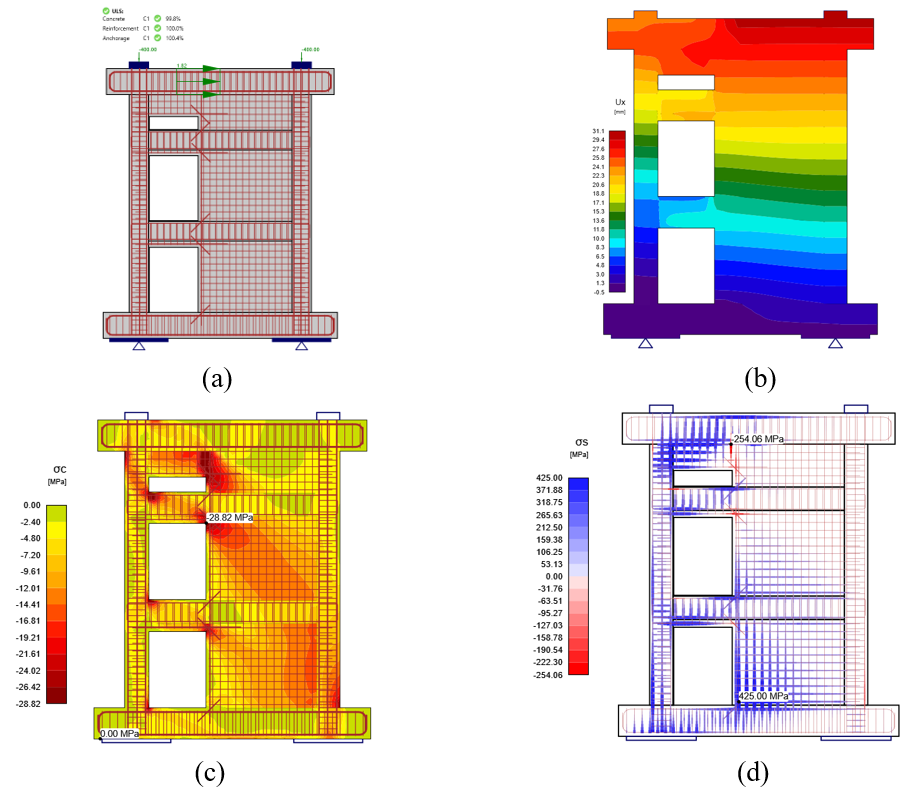
Figura 3.5: Muro cortante con aberturas L1 a 1.82 kN/mm (10.4 kip/in.) carga lateral: a) Modelo IDEA StatiCa Detail con resultados, b) contorno de deflexión, c) tensiones principales del hormigón (σc), y d) tensiones en la armadura (σs).

Cálculo de capacidad utilizando el modelo de puntales y tirantes

Las capacidades para todos los muros de cortante con aberturas se determinaron siguiendo las disposiciones para el Modelo de Puntal y Tirante (STM) como se indica en el código del Instituto Americano del Hormigón (ACI 318-19), descrito específicamente en la Sección 2.2. Dependiendo de la ubicación de las zonas nodales y de los puntales en el, factor de modificación del confinamiento de puntales y nodos (_βc), coeficiente de puntal(_βs) _y coeficiente de zona nodal(_βn) se tomaron de las Tablas 2.1 a 2.3 del Capítulo 2, respectivamente. La resistencia efectiva a compresión del hormigón(_fce) en un puntal y en una zona nodal se calculó mediante las ecuaciones 2.4 y 2.9, respectivamente.

Se desarrollaron múltiples modelos de riostras y tirantes para identificar el mejor modelo que produjera la máxima capacidad de carga lateral y la localización del fallo con la mayor precisión posible. Para construir los modelos de celosía (o STM con puntales como elementos de celosía a compresión y tirantes como elementos de celosía a tracción), se utilizaron diagramas de flujo de tensiones y gráficos de optimización topológica del análisis StatiCa de IDEA para todas las muestras de muros de cortante. El volumen efectivo fue del 20% en los gráficos de optimización topológica generados por IDEA StatiCa.

El desarrollo de un modelo de celosía o STM implica la creación de una representación simplificada del comportamiento estructural complejo utilizando principios de equilibrio de fuerzas y distribución de tensiones. El enfoque específico para diseñar el modelo de celosía puede variar significativamente, dependiendo del juicio, las preferencias y la experiencia de los ingenieros estructurales involucrados. Los ingenieros eligen entre una variedad de métodos para construir el modelo de celosía, con el objetivo de representar con precisión cómo se transmiten y distribuyen las tensiones y fuerzas dentro de la estructura. Este proceso tiene por objeto garantizar que el modelo de celosía represente eficazmente el comportamiento físico global y la integridad estructural, y que sea coherente con los requisitos de carga del diseño.

La navegación por los requisitos descritos en los códigos y normas, como los de la norma ACI 318-19 (especialmente en el capítulo 23), presenta varios retos en el desarrollo de un modelo de celosía o STM. Estas normas especifican factores críticos como el tamaño de los elementos, la conectividad y las trayectorias de carga para garantizar la integridad estructural y la seguridad en distintas condiciones de carga. Los requisitos específicos incluyen garantizar que todos los nodos estén en equilibrio, equilibrar las fuerzas verticales y horizontales en los puntales inclinados en las zonas nodales y evitar que los puntales y los tirantes se crucen. Además, los puntales deben mantener un ángulo de inclinación mínimo de 25 grados, y tanto los puntales como las zonas nodales deben estar dimensionados adecuadamente para soportar las cargas aplicadas. Las dimensiones de las riostras y de las zonas nodales se determinan en función de las resistencias efectivas del hormigón definidas en los apartados 2.3 y 2.4 del capítulo 2.

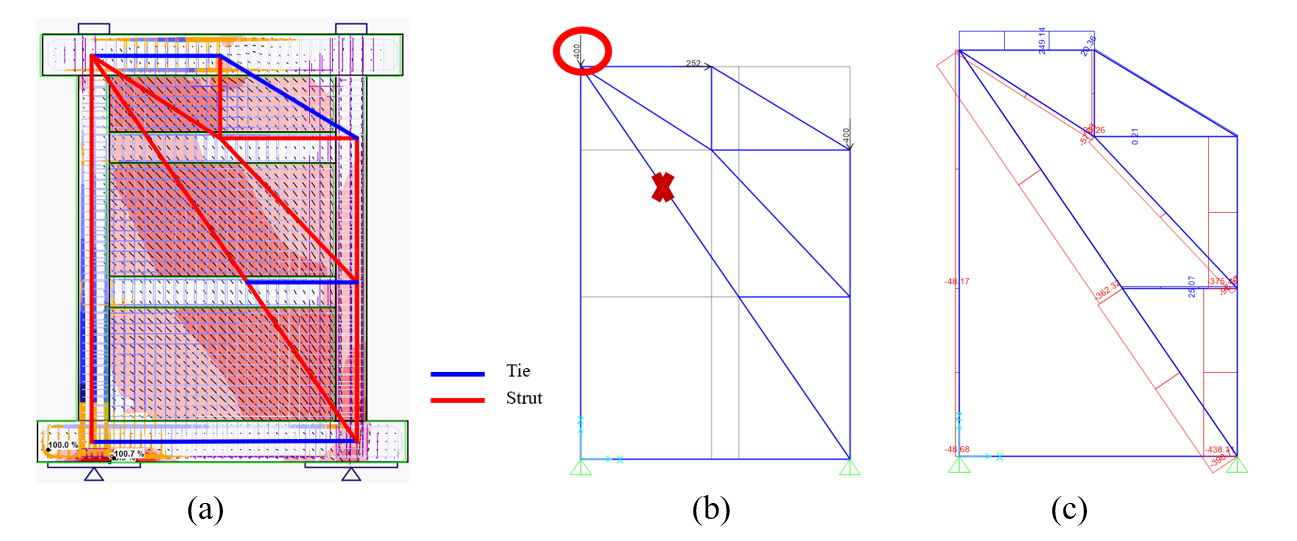
Basado en el diagrama de optimización topológica y los diagramas de flujo de tensiones determinados a partir del análisis IDEA StatiCa para el espécimen de muro cortante N1, se desarrollaron varios modelos de celosía. A continuación, estas cerchas se analizaron utilizando el software SAP2000 (2024). Este proceso se centró en dos objetivos principales: (a) identificar las riostras, los tirantes y las zonas nodales críticas (utilizando diagramas de flujo de tensiones del análisis StatiCa de IDEA) y (b) evaluar la capacidad de carga de cada modelo (utilizando las fuerzas de reacción y los miembros de la celosía del análisis SAP2000). Tras múltiples iteraciones, se presentaron los resultados del STM final y se compararon con los datos de ensayo medidos.

Figura 3.269: Modelo de puntales y tirantes para el espécimen N1: a) STM con flujo de tensiones, b) STM en SAP2000, y c) fuerzas axiales en los miembros STM calculadas en SAP2000.

Desarrollo y análisis del modelo ABAQUS

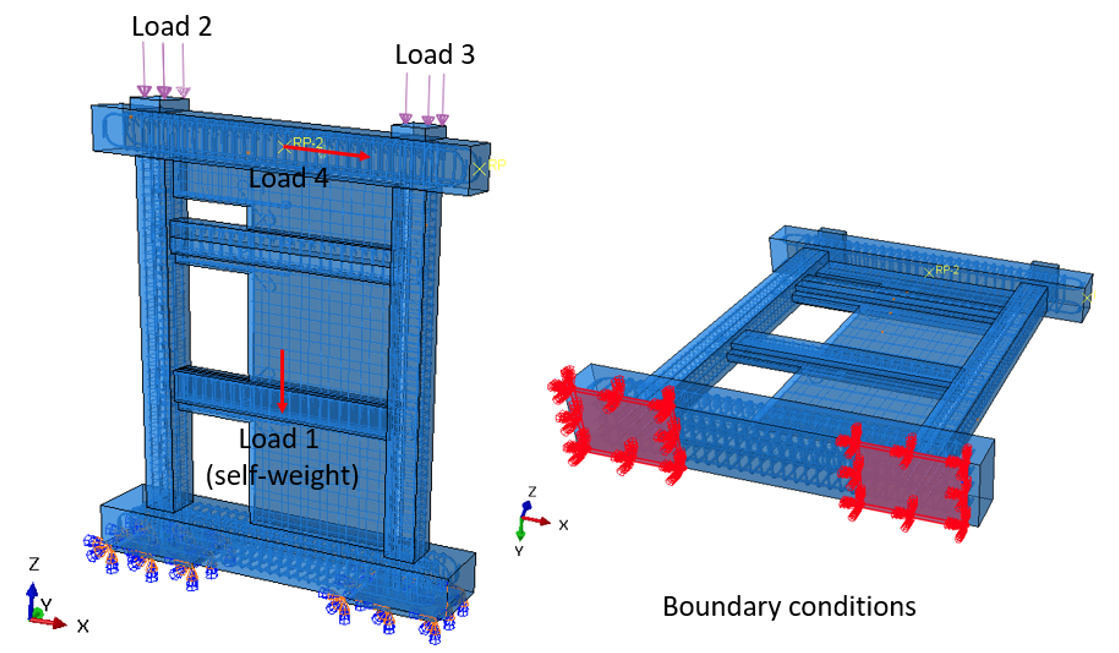
En esta sección, el espécimen L1, que fue modelado y analizado en la Sección 3.5.1, fue remodelado utilizando el software ABAQUS (2023) para el análisis de elementos finitos (FE). A continuación, se compararon los resultados con los obtenidos con IDEA StatiCa. Debido a la complejidad de la estructura, el modelo CAD, incluyendo el hormigón y las barras de refuerzo, se dibujó en el software Rhino (McNeel, 2020) y luego se exportó a ABAQUS como un archivo STEP. La versión de Rhino utilizada se incluirá en las Referencias. De forma similar al modelo IDEA StatiCa, en ABAQUS, además del peso propio (es decir, Carga 1), se aplicaron dos cargas verticales (es decir, Cargas 2 y 3), cada una de 400 kN, a dos placas portantes con un espesor de 4 pulgadas, tal y como se muestra en la Figura 3.34. Dado que la carga lineal sólo puede utilizarse para elementos viga en ABAQUS, para imitar la carga lateral impuesta a la estructura en el ensayo experimental y en IDEA StatiCa, se aplicó una fuerza horizontal (es decir, la Carga 4) a un punto de referencia definido (es decir, RF2) que se acopló a los bordes de la viga superior para asemejarse a la carga lineal.

Figura 3.34: Configuración del modelo en ABAQUS mostrando las ubicaciones y detalles de la carga aplicada y las condiciones de contorno.

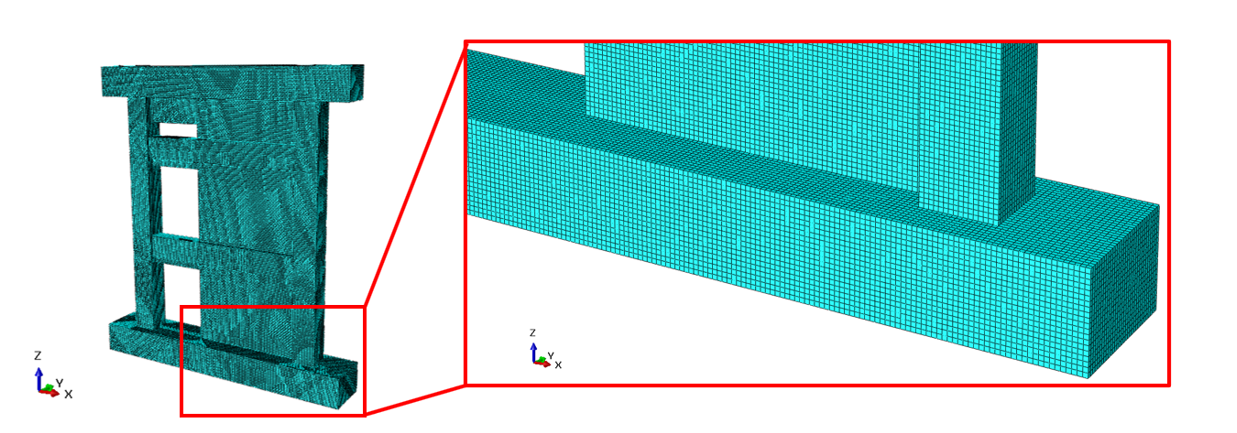
Se fijaron dos placas de soporte bajo la estructura para restringir el desplazamiento vertical y lateral (ver Figura 3.34). Para capturar con precisión el inicio y la evolución de la grieta, se eligió un tamaño de elemento de 20 mm, resultando un total de 396.505 elementos en el modelo (ver Figura 3.35). Para el hormigón se seleccionó el tipo de elemento 3D stress, 8-node linear brick reduced integration (i.e., C3D8R), mientras que para las barras de refuerzo se eligió el elemento truss.

Figura 3.35: Densidad de malla con un tamaño de elemento de 20 mm.

En ABAQUS, se utilizó el modelo constitutivo Concrete Damage Plasticity (CDP). Los parámetros necesarios para describir este modelo se obtuvieron tras su calibración de diversas fuentes (Federal Highway Administration, 2006, y Watanabe et al., 2004), ya que no se indicaban explícitamente en Taleb et al. (2012). Para las barras de acero, el comportamiento del material se modeló mediante plasticidad bilineal. Otros parámetros, incluyendo la densidad, el módulo elástico y la relación de Poisson, se tomaron exactamente de la biblioteca de materiales IDEA StatiCa. La simulación numérica se llevó a cabo en una máquina virtual con 16 procesadores (Intel Xeon® Gold Processor 6430 @2.10GHz) y tardó aproximadamente 185 minutos en finalizar, mientras que IDEA StatiCa completó el cálculo en menos de dos minutos.

Resumen

En conclusión, se evaluaron las capacidades de muros de cortante de hormigón armado con aberturas utilizando IDEA StatiCa Detail, comparando el modelo de puntales y tirantes de ACI 318-19, ABAQUS, el Método de Campo de Esfuerzos Compatibles (CSFM) y datos experimentales. El estudio reveló que el STM subestimaba significativamente la capacidad de carga debido a sus hipótesis de diseño conservadoras. Por el contrario, tanto el CSFM como ABAQUS proporcionaron resultados que se alineaban estrechamente con las capacidades medidas, especialmente en condiciones de carga positiva. Además, el análisis consideró los efectos del material de hormigón confinado frente al no confinado sobre la resistencia y el comportamiento a la deriva. Los resultados mostraron que, en general, el confinamiento mejora la capacidad del muro de cortante, aunque el impacto en los ángulos de deriva varía según las muestras. En general, los resultados ponen de relieve la importancia de seleccionar los métodos de predicción adecuados, con CSFM y ABAQUS demostrando una precisión superior en comparación con STM y subrayan la necesidad de una cuidadosa consideración de los efectos de confinamiento en el diseño y análisis.

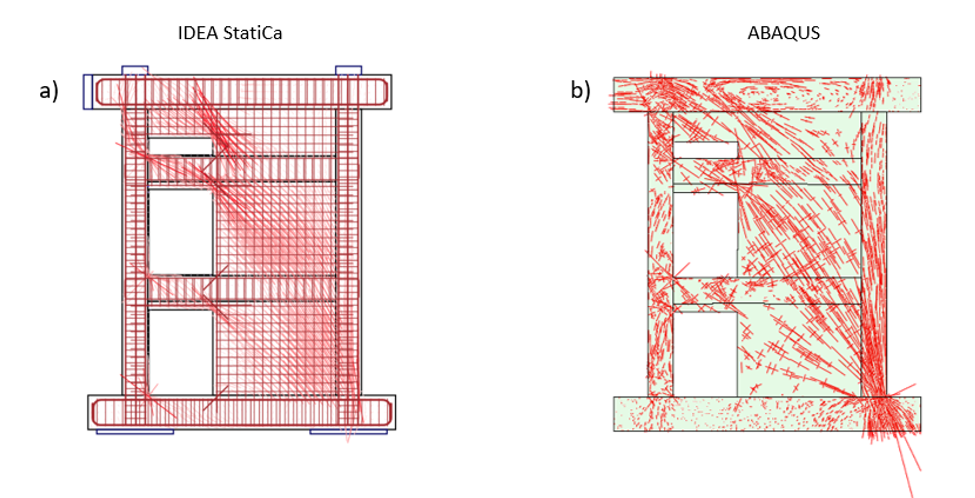
Figura 3.39: Comparación de la dirección de las tensiones principales entre IDEA StatiCa y ABAQUS.

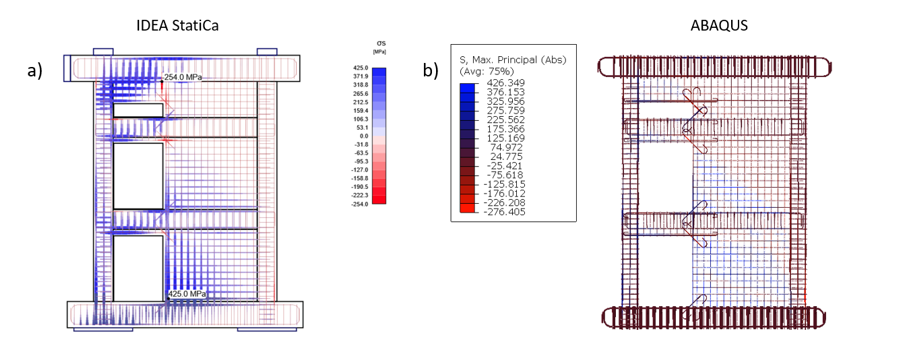
Figura 3.41: Comparación de las tensiones en las barras de acero entre a) IDEA StatiCa, y b) ABAQUS.