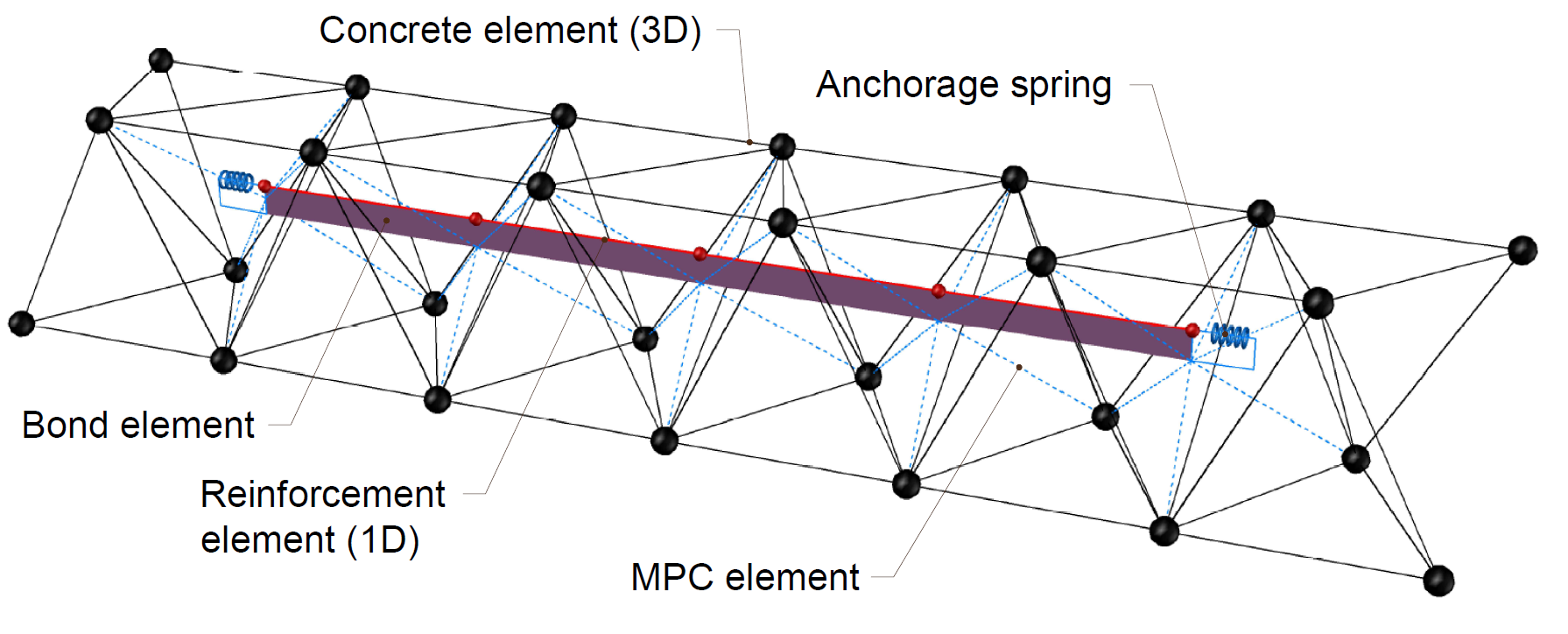
El modelo de análisis de elementos finitos no lineal (inelástico) se crea mediante varios tipos de elementos finitos utilizados para modelizar el hormigón, la armadura y la unión entre ellos. Los elementos de hormigón y armadura se mallan primero de forma independiente y luego se interconectan mediante restricciones multipunto (elementos MPC). Esto permite que la armadura ocupe cualquier posición no limitada a los nodos de la malla tetraédrica. Para verificar la longitud de anclaje, la unión y el extremo de anclaje se insertan elementos de muelle entre la armadura y los elementos MPC.
\[ \textsf{\textit{\footnotesize{Fig. 10\qquad Modelo de elementos finitos: elementos de refuerzo mapeados a la malla de hormigón utilizando elementos MPC y de enlace}} {}]
Hormigón
El hormigón se analiza utilizando elementos tetraédricos mixtos con rotaciones nodales. Los elementos tetraédricos nos permiten mallar regiones de cualquier topología mientras que la formulación implementada garantiza resultados de deformación precisos (sin esfuerzos cortantes espurios conocidos como efecto shear lock) incluso para la malla gruesa que no sería adecuada para la formulación de elementos tetraédricos lineales.
Se utiliza la integración completa. Esto significa que cada elemento está equipado con cuatro puntos de integración situados dentro del volumen. Esta integración permite obtener un campo de deformaciones y tensiones preciso, lo que permite evaluar y presentar los resultados de forma suficiente en todo el volumen. Posteriormente, los criterios de parada se establecen en función del valor en el punto de integración.
Refuerzo
Las armaduras se modelizan mediante elementos "varilla" 1D de dos nodos (CROD), que sólo tienen rigidez axial. Estos elementos están conectados a elementos especiales de "unión" que se desarrollaron para modelar el comportamiento de deslizamiento entre una barra de refuerzo y el hormigón circundante. Estos elementos de unión se conectan posteriormente mediante elementos MPC (restricción multipunto) a la malla que representa el hormigón. Este planteamiento permite el mallado independiente de la armadura y el hormigón, mientras que su interconexión se garantiza posteriormente.
Elementos de unión
La longitud de anclaje se verifica implementando los esfuerzos cortantes de enlace entre los elementos de hormigón (3D) y los elementos de armadura (1D) en el modelo de elementos finitos. Para ello, se ha desarrollado el tipo de elemento finito "enlace".
El elemento de unión se define como un elemento finito de cáscara conectado a los elementos que representan el refuerzo por la primera capa y por la segunda capa a la malla de hormigón mediante restricciones multipunto (elementos MPC). Cabe señalar que el elemento de unión siempre se muestra en este artículo con una altura distinta de cero, que, sin embargo, se define como infinitesimal en el modelo.
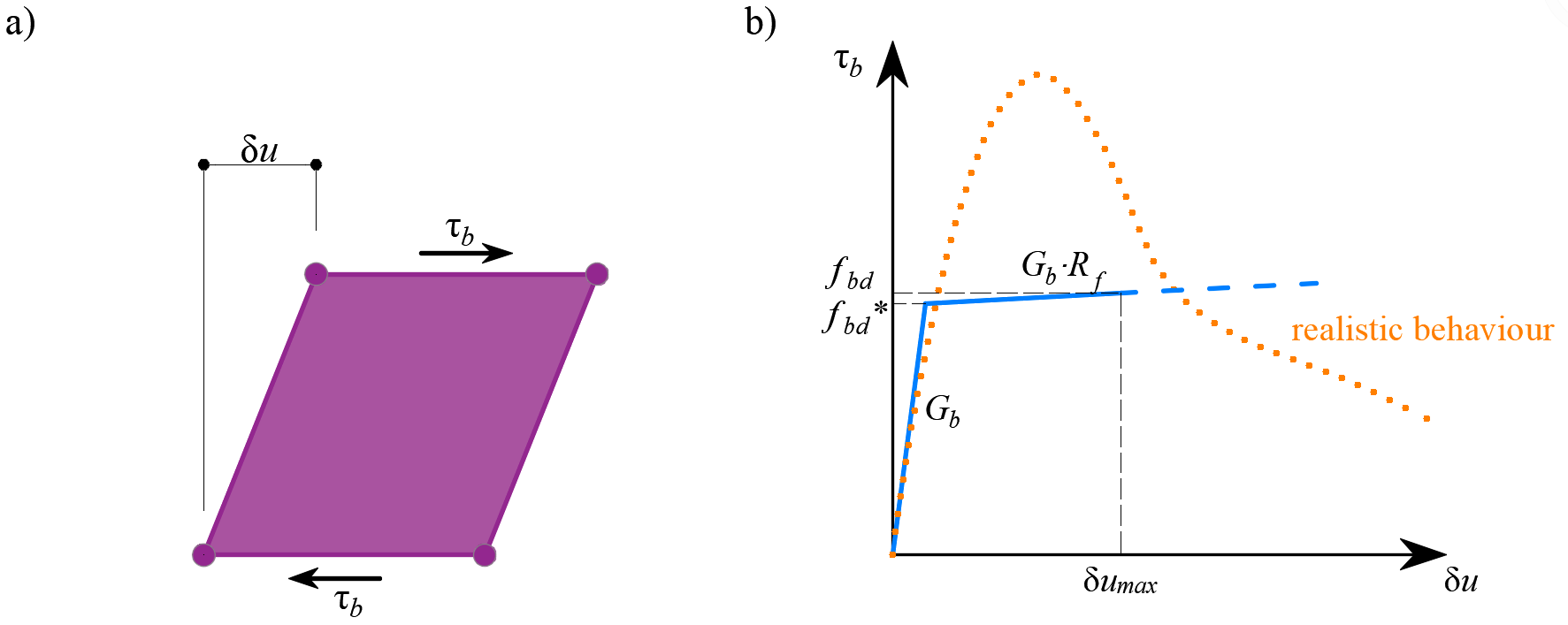
El comportamiento de este elemento se describe por la tensión de adherencia, τb, como una función bilineal del deslizamiento entre los nudos superior e inferior, δu, ver (Fig. 11).
\[ \textsf{\textit{footnotesize{Fig. 11\qquad (a) Ilustración conceptual de la deformación de un elemento de unión; (b) función cizalladura-deformación}}}]
El módulo de rigidez elástica de la relación adherencia-deslizamiento, Gb, se define como sigue:
\[G_b = k_g \cdot \frac{E_c}{Ø}]
coeficiente kg en función de la superficie de la barra de armadura (por defecto kg = 0,2)
Ec módulo de elasticidad del hormigón (tomado como Ecm en el caso de EN)
Ø diámetro de la armadura
Para verificar la longitud de anclaje se utilizan los valores de cálculo (valores factorizados) del esfuerzo cortante último de adherencia, fbd, proporcionados en los respectivos códigos de cálculo seleccionados EN 1992-1-1 o ACI 318-19. El endurecimiento de la rama plástica se calcula por defecto como Gb/105.
Muelle de anclaje
La provisión de extremos de anclaje a las barras de armadura (es decir, codos, ganchos, lazos...), que cumple las prescripciones de los códigos de diseño, permite reducir la longitud de anclaje básica de las barras(lb,net) en un determinado factor β (denominado a continuación "coeficiente de anclaje"). El valor de diseño de la longitud de anclaje(lb) se calcula entonces de la siguiente manera:
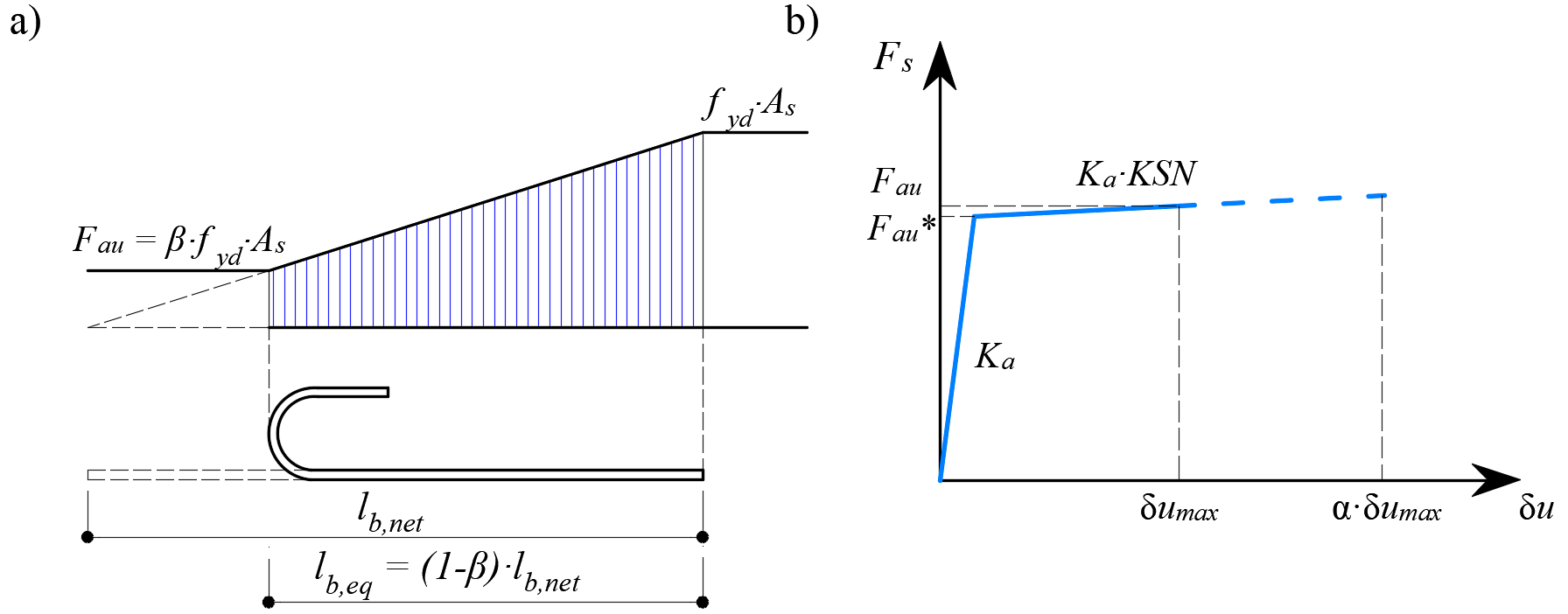
\[ \textsf{\textit{footnotesize{Fig. 12\qquad Modelo para la reducción de la longitud de anclaje: a) Fuerza de anclaje a lo largo de la longitud de anclaje de }}}]. \[ \textsf{textit{footnotesize{la barra de refuerzo, b) ley constitutiva de la fuerza de deslizamiento-anclaje}}}]
La reducción de la longitud de anclaje se incluye en el modelo de elementos finitos mediante un elemento muelle en el extremo de la barra (Fig. 12a), que viene definido por el modelo constitutivo mostrado en (Fig. 12b). La fuerza máxima transmitida por este muelle(Fau) es:
\[F_{au} = \beta \cdot A_s \cdot f_{yd}\]
donde :
β el coeficiente de anclaje en función del tipo de anclaje
Como la sección transversal de la barra de refuerzo
fyd el valor de cálculo (valor factorizado) del límite elástico de la armadura