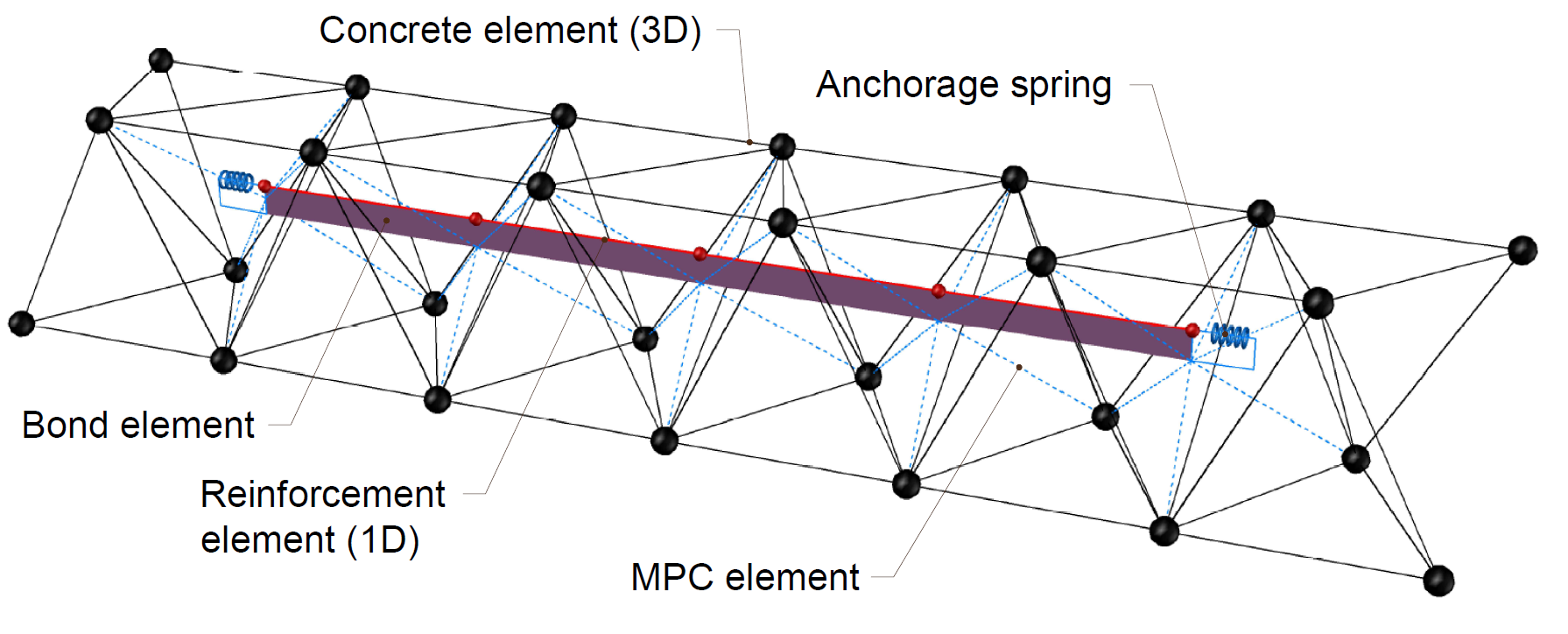
O modelo de análise de elementos finitos não linear (inelástico) é criado por vários tipos de elementos finitos utilizados para modelar o betão, a armadura e a ligação entre eles. Os elementos de betão e de armadura são inicialmente malhados de forma independente e depois interligados através de restrições multiponto (elementos MPC). Isto permite que o reforço ocupe qualquer posição não limitada aos nós da malha tetraédrica. Para verificar o comprimento da ancoragem, a ligação e a extremidade da ancoragem, são inseridos elementos de mola entre a armadura e os elementos MPC.
\[ \textsf{\textit{\footnotesize{Fig. 10\qquad Modelo de elementos finitos: elementos de reforço mapeados para a malha de betão utilizando elementos MPC e de ligação}}}\]
Betão
O betão é analisado utilizando elementos tetraédricos mistos com rotações nodais. Os elementos tetraédricos permitem-nos criar malhas em regiões de qualquer topologia, enquanto a formulação implementada garante resultados de deformação precisos (sem tensões de corte espúrias, conhecidas como efeito de bloqueio de corte), mesmo para malhas grosseiras que não seriam adequadas para a formulação de elementos tetraédricos lineares.
É utilizada a integração total. Isto significa que cada elemento está equipado com quatro pontos de integração situados dentro do volume. Esta integração produz um campo preciso de deformação e tensão, permitindo uma avaliação e apresentação suficientes dos resultados em todo o volume. Posteriormente, os critérios de paragem são estabelecidos com base no valor do ponto de integração.
Reforço
As armaduras são modeladas por elementos de "barra" 1D de dois nós (CROD), que apenas têm rigidez axial. Estes elementos são ligados a elementos especiais de "ligação" que foram desenvolvidos para modelar o comportamento de deslizamento entre um varão de reforço e o betão circundante. Estes elementos de ligação são posteriormente ligados por elementos MPC (multi-point constraint) à malha que representa o betão. Esta abordagem permite a criação de malhas independentes para a armadura e para o betão, enquanto a sua interligação é assegurada posteriormente.
Elementos de ligação
O comprimento de ancoragem é verificado através da implementação das tensões de corte de ligação entre os elementos de betão (3D) e os elementos do varão de reforço (1D) no modelo de elementos finitos. Para este efeito, foi desenvolvido o tipo de elemento finito "ligação".
O elemento de ligação é definido como um elemento finito de casca ligado a elementos que representam a armadura pela primeira camada e pela segunda camada à malha de betão através de restrições multiponto (elementos MPC). É de notar que o elemento de ligação é sempre apresentado neste artigo com uma altura diferente de zero, que é, no entanto, definida como infinitesimal no modelo.
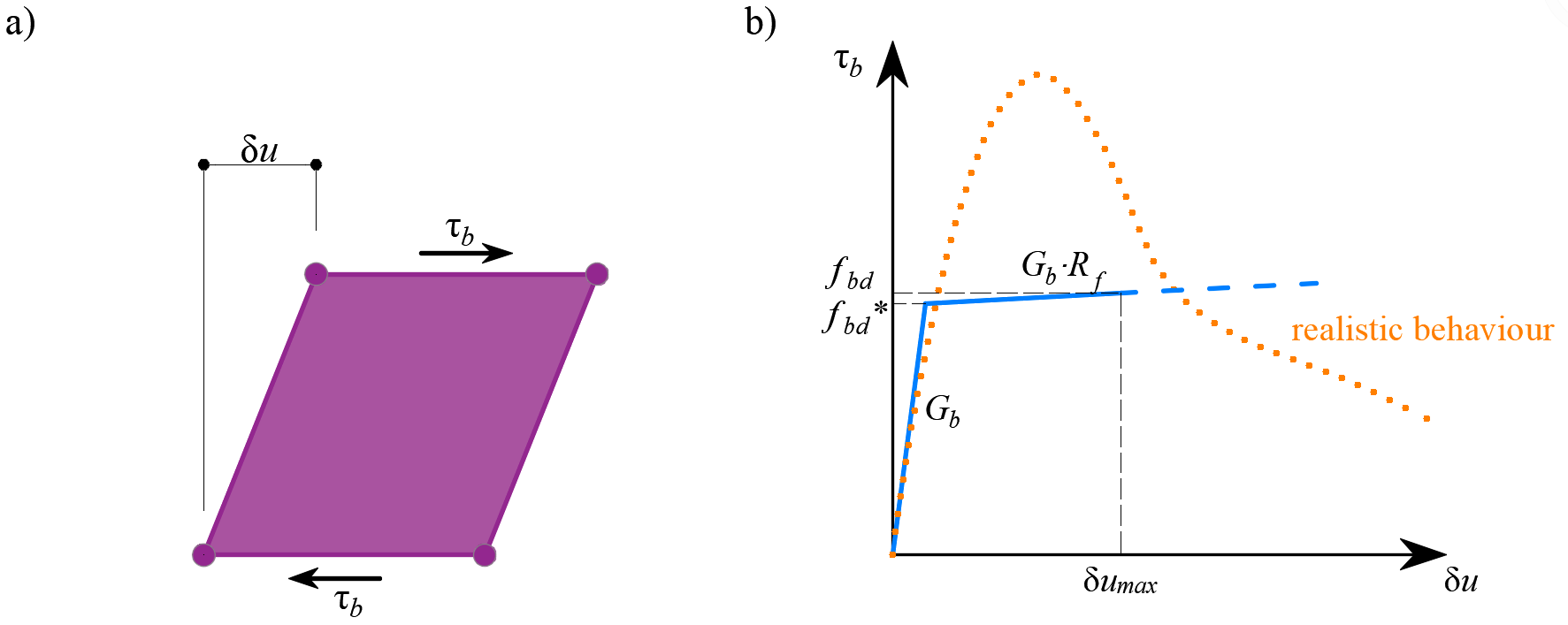
O comportamento deste elemento é descrito pela tensão de ligação, τb, como uma função bilinear do deslizamento entre os nós superior e inferior, δu, ver (Fig. 11).
\[ \textsf{\textit{\footnotesize{Fig. 11\qquad (a) Ilustração concetual da deformação de um elemento de ligação; (b) função de deformação de corte}}}\]
O módulo de rigidez elástica da relação ligação-deslizamento, Gb, é definido da seguinte forma:
\[G_b = k_g \cdot \frac{E_c}{Ø}\]
kg coeficiente dependente da superfície do varão de reforço (por defeito, kg = 0,2)
Ec módulo de elasticidade do betão (tomado como Ecm no caso de EN)
Ø o diâmetro do varão de reforço
Os valores de cálculo (valores ponderados) da tensão última de corte da ligação, fbd, fornecidos nos respectivos códigos de cálculo selecionados EN 1992-1-1 ou ACI 318-19 são utilizados para verificar o comprimento da ancoragem. O endurecimento do ramo plástico é calculado por defeito como Gb/105.
Mola de ancoragem
O fornecimento de extremidades de ancoragem aos varões de reforço (i.e., curvas, ganchos, laços...), que cumprem as prescrições dos códigos de dimensionamento, permite a redução do comprimento de ancoragem básico dos varões(lb,net) por um determinado fator β (referido como o "coeficiente de ancoragem" abaixo). O valor de projeto do comprimento de ancoragem(lb) é então calculado da seguinte forma:
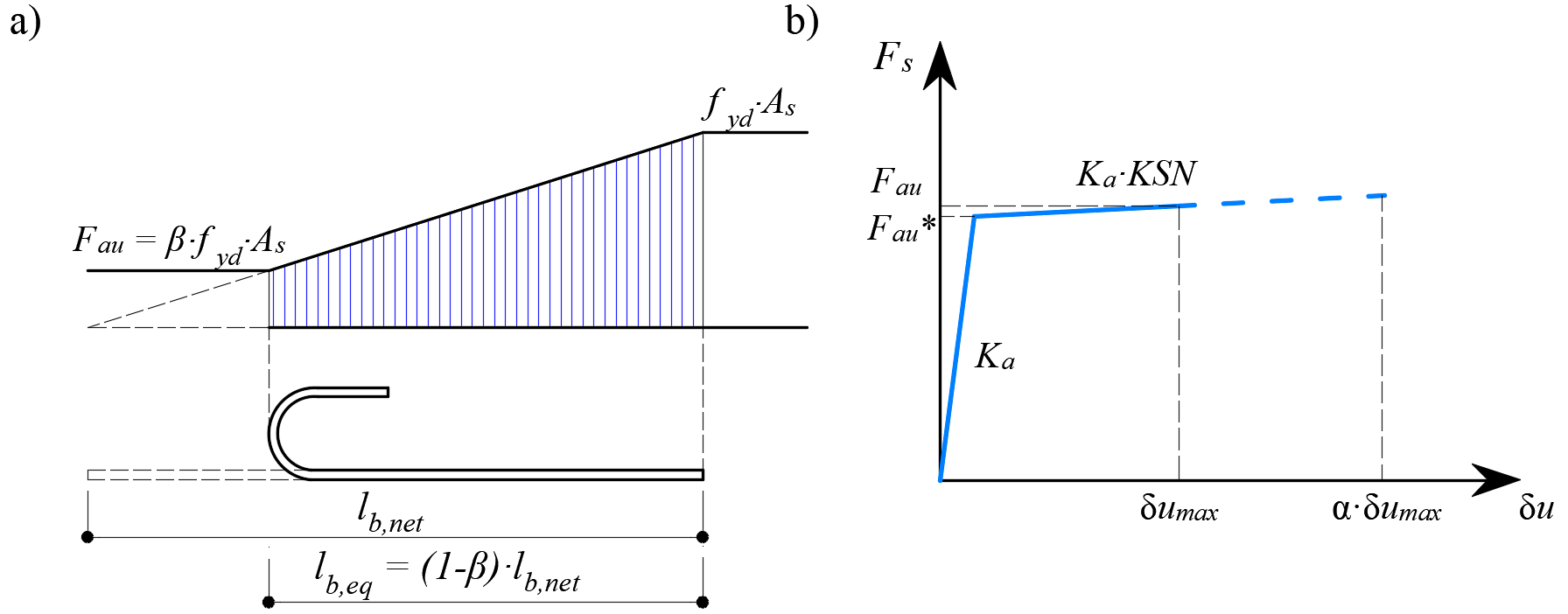
\[ \textsf{\textit{\footnotesize{Fig. 12\qquad Modelo para a redução do comprimento de ancoragem: a) Força de ancoragem ao longo do comprimento de ancoragem de }}}\] \[ \textsf{\textit{\footnotesize{a barra de reforço, b) lei constitutiva da força de ancoragem por deslizamento}}\]
A redução do comprimento de ancoragem é incluída no modelo de elementos finitos através de um elemento de mola na extremidade da barra (Fig. 12a), que é definido pelo modelo constitutivo apresentado na (Fig. 12b). A força máxima transmitida por esta mola(Fau) é:
\[F_{au} = \beta \cdot A_s \cdot f_{yd}\]
onde :
β o coeficiente de ancoragem baseado no tipo de ancoragem
Como a secção transversal do varão de reforço
fyd o valor de projeto (valor calculado) da tensão de cedência da armadura