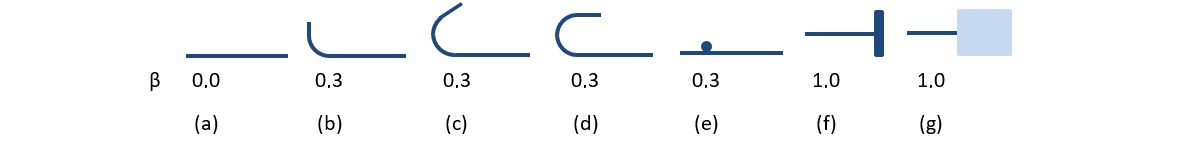As diferentes verificações exigidas pela norma EN 1992-1-1 são avaliadas com base nos resultados diretos fornecidos pelo modelo. As verificações ULS são efectuadas para a resistência do betão, a resistência das armaduras e a ancoragem (tensões de corte da ligação).
A resistência do betão à compressão é avaliada como o rácio entre a tensão principal equivalente máxima σc,eq obtida da análise de EF e o valor limite σc,lim = fcd.
A tensão principal equivalente expressa a tensão uni-axial equivalente para um estado de tensão tri-axial geral.
\[\sigma_{c,eq} = \sigma_{c3} - \sigma_{c1}\]
O valor σc,eq pode, portanto, ser diretamente comparado com os limites de resistência uniaxial de acordo com 1992-1-1 Cl. 3.1.7 (1).
Esta expressão é derivada da implementação da teoria da plasticidade de Mohr-Coulomb, assumindo conservadoramente o ângulo de atrito interno φ = 0°.
A resistência da armadura é avaliada tanto em tração como em compressão como a relação entre a tensão na armadura nas fissuras σsr e o valor limite especificado σs,lim:
\(σ_{s,lim} = \frac{k \cdot f_{yk}}{γ_s}\qquad\qquad\textsf{\small{para diagrama bilinear com ramo superior inclinado}}\)
\(σ_{s,lim} = \frac{f_{yk}}{γ_s}\qquad\qquad\,\,\,\,\,\textsf{\small{para diagrama bilinear com ramo superior horizontal}}\)
em que:
fyk é a tensão de cedência da armadura de acordo com a norma EN 1992-1-1 Cl. 3.2.3,
k é o rácio entre a resistência à traçãoftk e a tensão de cedência,
\(k = \frac{f_{tk}}{f_{yk}}\)
γs é o fator de segurança parcial para o reforço.
A tensão de corte da ligação é avaliada independentemente como o rácio entre a tensão da ligação τb calculada pela análise de EF e a resistência final da ligação fbd, de acordo com a norma EN 1992-1-1 cap. 8.4.2:
\[\frac{τ_{b}}{f_{bd}}\le 1\]
\[f_{bd} = 2,25 \cdot η_1\cdot η_2\cdot f_{ctd}\]
em que:
fctd é o valor de projeto da resistência à tração do betão de acordo com a norma EN 1992-1-1 Cl. 3.1.6 (2). Devido à fragilidade crescente do betão de resistência mais elevada, fctk,0.05 é limitado ao valor para C60/75 de acordo com a norma EN 1992-1-1 Cl. 8.4.2 (2)
η1 é um coeficiente relacionado com a qualidade da condição de ligação e a posição da barra durante a betonagem (Fig. 31).
η1 = 1,0 quando se obtêm "boas" condições e
η1 = 0,7 para todos os outros casos e para barras em elementos estruturais construídos com formas deslizantes, a menos que se possa demonstrar que existem "boas" condições de ligação
η2 está relacionado com o diâmetro da barra:
η2 = 1,0 para Ø ≤ 32 mm
η2 = (132 - Ø)/100 para Ø > 32 mm
\[ \textsf{\textit{\footnotesize{Fig. 20\qquad EN 1992-1-1 Figura 8.2 - Descrição das condições de ligação.}}}\]
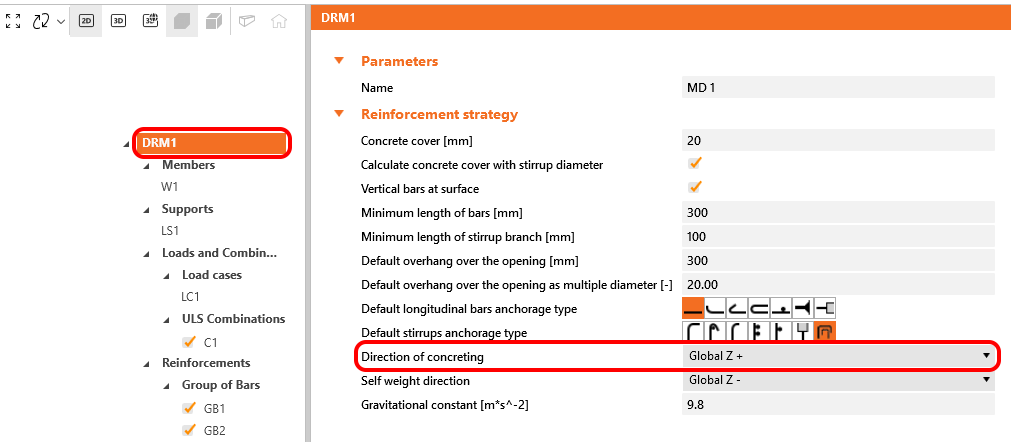
No IDEA StatiCa Detail, as condições de ligação são tidas em conta de acordo com a Fig. 20 c) e d). A direção da betonagem pode ser definida na aplicação para cada item do projeto da seguinte forma:
\[ \textsf{\textit{\footnotesize{Fig. 21\qquad Direção de betonagem}}}\]
Estas verificações são efectuadas em relação aos valores-limite apropriados para as respectivas partes da estrutura (isto é, apesar de haver uma única classe para o betão e para o material de reforço, os diagramas finais de tensão-deformação serão diferentes em cada parte da estrutura devido aos efeitos de enrijecimento por tração e amolecimento por compressão).
Força total Ftot e força limite Flim
A força total Ftot é o resultado da análise de elementos finitos e pode ser definida de duas formas.
\[F_{tot}=A_{s}\cdot \sigma_{s}\]
ondeAs é a área da barra de reforço e σs é a tensão na barra.
Ou como uma soma da força de ancoragemFa e da força de ligação Fbond.
\[F_{tot}=F_{a}+F_{bond}\]
em queFa é a força real na mola de ancoragem e Fbond é a força de ligação que pode ser obtida através da integração da tensão de ligação τb ao longo do comprimento da barra de reforço l.
\[F_{bond}=C_{s} \cdot \int_{0}^{l}\tau_{b}\left( x \right)dx\]
Cs é a circunferência do varão de reforço.
A força limiteFlim é a força máxima no elemento do varão considerando a resistência última do varão e também as condições de ancoragem (ligação entre o betão e a armadura e ganchos de ancoragem, laços, etc.).
\[F_{lim}=min\left( F_{lim,bond}+F_{au},F_{u} \right)\]
\[F_{u}=k\cdot f_{yd}\cdot A_{s}\]
\[F_{au}=\beta\cdot k\cdot f_{yd}\cdot A_{s}\]
\[F_{lim,bond}=C_{s}\cdot l \cdot f_{bd}\]
em que Cs é a circunferência da barra de reforço e l é o comprimento desde o início da barra de reforço até ao ponto de interesse.
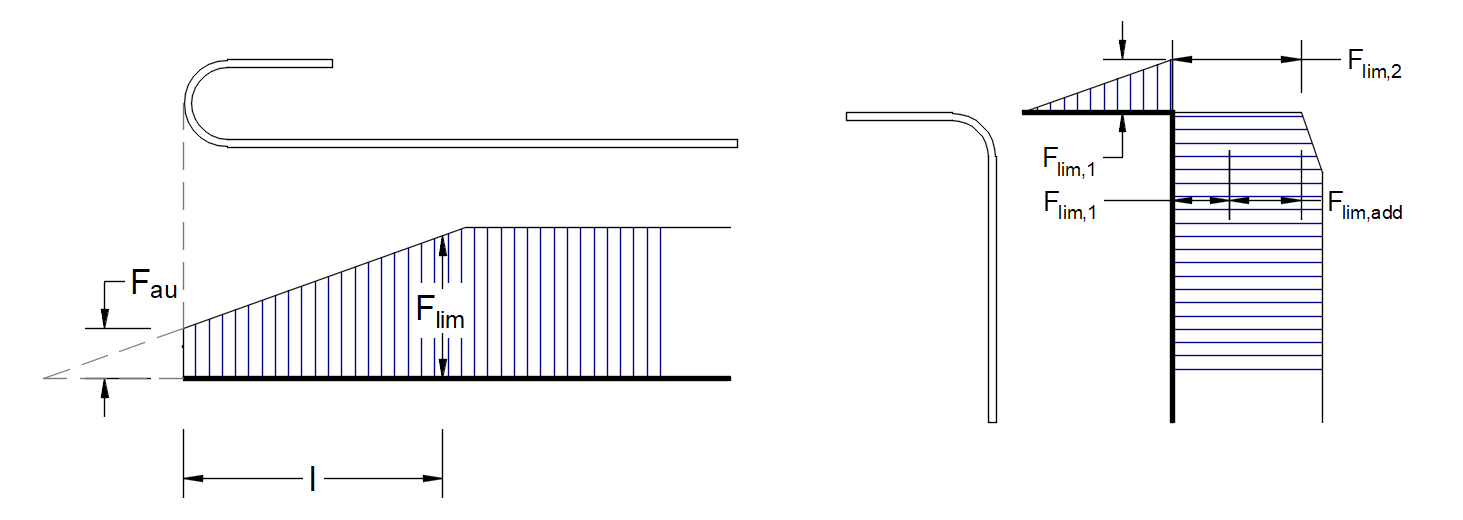
\[ \textsf{\textit{\footnotesize{Fig. 22\qquad Definição da força limite Flim}}\]
\[F_{lim,2}=F_{lim,1}+F_{lim,add}\]
em queFlim,add é a força adicional calculada a partir da magnitude do ângulo entre elementos vizinhos.Flim,2 deve ser sempre inferior aFu.
Os tipos de ancoragem disponíveis no CSFM 3D incluem uma barra reta (i.e., sem redução da extremidade da ancoragem), curva, gancho, laço, barra transversal soldada, ligação perfeita e barra contínua. Todos estes tipos, juntamente com os respectivos coeficientes de ancoragem β, são apresentados na Fig. 23 para a armadura longitudinal e na Fig. 24 para os estribos. Os valores dos coeficientes de ancoragem adoptados estão de acordo com a norma EN 1992-1-1, secção 8.4.4 Tab. 8.2. É de notar que, apesar das diferentes opções disponíveis, o CSFM 3D distingue três tipos de extremidades de ancoragem: (i) nenhuma redução no comprimento da ancoragem, (ii) uma redução de 30% do comprimento da ancoragem no caso de uma ancoragem normalizada, e (iii) ligação perfeita.
\[ \textsf{\textit{\footnotesize{Fig. 23\qquad Tipos de ancoragem disponíveis e respetivos coeficientes de ancoragem para varões de reforço longitudinal no CSFM 3D:}}}\]
\[ \textsf{\textit{\footnotesize{(a) varão reto; (b) dobra; (c) gancho; (d) laço; (e) varão transversal soldado; (f) ligação perfeita; (g) varão contínuo.}}}\]
\[ \textsf{\textit{\footnotesize{Fig. 24\qquad Tipos de ancoragem disponíveis e respectivos coeficientes de ancoragem para estribos.}}}\]
\[ \textsf{\textit{\footnotesize{Estribos fechados: (a) gancho; (b) dobra; (c) sobreposição. Estribos abertos: (d) gancho; (e) barra contínua.}}}\]
Para cumprir a norma EN 1992-1-1, a mola de ancoragem deve ser utilizada no cálculo, a mola de ancoragem é modificada pelo coeficiente β, pelo que o utilizador deve utilizar um dos tipos de ancoragem disponíveis ao definir as condições de início e fim da armadura.