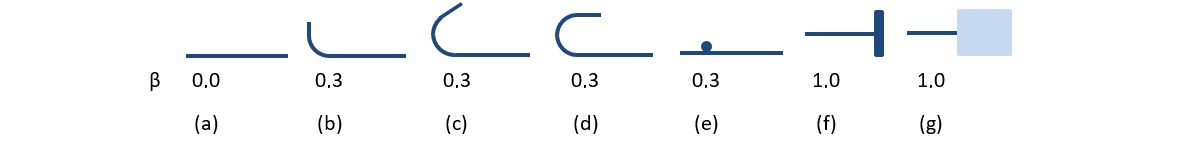De verschillende door EN 1992-1-1 vereiste verificaties worden beoordeeld op basis van de directe resultaten van het model. UGT-verificaties worden uitgevoerd voor betonsterkte, wapeningssterkte en verankering (afschuifspanningen).
De betonsterkte in druk wordt geëvalueerd als de verhouding tussen de maximale equivalente hoofdspanning σc,eq verkregen uit de FE-analyse en de grenswaarde σc,lim = fcd.
De equivalente hoofdspanning drukt de equivalente uni-axiale spanning uit voor een algemene tri-axiale spanningstoestand.
\[\sigma_{c,eq} = \sigma_{c3} - \sigma_{c1}\]
De σc,eq waarde kan daarom direct worden vergeleken met de grenswaarden voor deuni-axiale sterkte volgens 1992-1-1 Cl. 3.1.7 (1).
Deze uitdrukking is afgeleid van de toepassing van de Mohr-Coulomb plasticiteitstheorie, waarbij conservatief is aangenomen dat de hoek van inwendige wrijving φ = 0°.
De sterkte van de wapening wordt zowel in trek als in druk geëvalueerd als de verhouding tussen de spanning in de wapening bij de scheuren σsr en de gespecificeerde grenswaarde σs,lim:
\(σ_{s,lim} = \frac{k \cdot f_{yk}}{γ_s}\qquad\qquad\textsf{\small{for bilinear diagram with inclined top branch}}\)
\(σ_{s,lim} = \frac{f_{yk}}{γ_s}\qquad\qquad\,\,\,\,\textsf{\small{for bilinear diagram with horizontal top branch}}\)
waarin:
fyk de vloeigrens van de wapening is volgens EN 1992-1-1 Cl. 3.2.3,
k de verhouding is tussen de treksterkte ftk en de vloeispanning, \(k = \frac{f_{tk}}{f_{yk}}\)
γs is de partiële veiligheidsfactor voor wapening.
De afschuifspanning van de aanhechting wordt onafhankelijk geëvalueerd als de verhouding tussen de bondstress τb berekend door FE-analyse en de uiteindelijke aanhechtsterkte fbd, volgens EN 1992-1-1 hoofdstuk. 8.4.2:
\[\frac{τ_{b}}{f_{bd}}\le 1\]
\[f_{bd} = 2.25 \cdot η_1\cdot η_2\cdot f_{ctd}\]
waarbij:
fctd de ontwerpwaarde is van de betontreksterkte volgens EN 1992-1-1 Cl. 3.1.6 (2). Vanwege de toenemende brosheid van beton met een hogere sterkte is fctk,0.05 beperkt tot de waarde voor C60/75 volgens EN 1992-1-1 Cl. 8.4.2 (2)
η1 is een coëfficiënt die verband houdt met de kwaliteit van de aanhechting en de positie van de staaf tijdens het betonstorten (Fig. 31).
η1 = 1,0 wanneer 'goede' omstandigheden worden verkregen en
η1 = 0,7 voor alle andere gevallen, tenzij kan worden aangetoond dat er 'goede' omstandigheden zijn.
η2 is gerelateerd aan de staafdiameter:
η2 = 1,0 voor Ø ≤ 32 mm
η2 = (132 - Ø)/100 voor Ø > 32 mm
\[ \textsf{\textit{\footnotesize{Fig. 20\qquad EN 1992-1-1 Figure 8.2 - Beschrijving van aanhechtingscondities.}}}\]
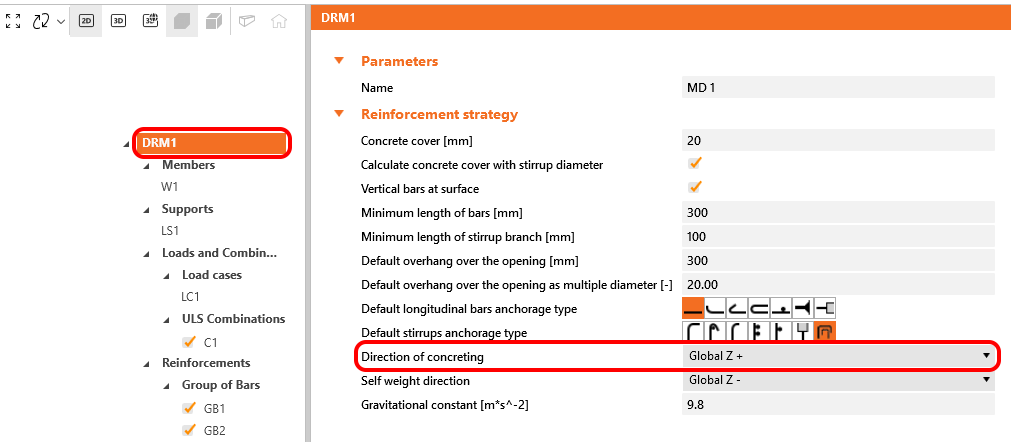
In IDEA StatiCa Detail wordt rekening gehouden met de omstandigheden volgens Fig. 20 c) en d). De betonstortrichting kan in de toepassing voor elk projectonderdeel als volgt worden ingesteld:
\[ \textsf{\textit{\footnotesize{Fig. 21\qquad Richting van betonstorten}}}\]
Deze controles worden uitgevoerd met betrekking tot de juiste grenswaarden voor de respectieve delen van de constructie (d.w.z. ondanks het feit dat er één klasse is voor zowel beton als wapeningsmateriaal, zullen de uiteindelijke spanning-rekdiagrammen verschillen in elk deel van de constructie vanwege verstijvings- en samendrukkingseffecten).
Totale kracht Ftot en limiet kracht Flim
De totale kracht Ftot is een resultaat van de eindige-elementenanalyse en kan op twee manieren worden gedefinieerd.
\[F_{tot}=A_{s}\cdot \sigma_{s}\]
waarbijAs de oppervlakte van de wapeningsstaaf is en σs de spanning in de staaf.
Of als een som van de verankeringskrachtFa en de aanhechtingskracht Fbond.
\[F_{tot}=F_{a}+F_{bond}\]
waarbijFa de werkelijke kracht in de verankeringsveer is en Fbond de aanhechtingskracht die kan worden verkregen door de aanhechtspanning τb te integreren langs de lengte van wapeningsstaaf l.
\[F_{bond}=C_{s} \cdot \int_{0}^{l}\tau_{b}\left( x \right)dx\]
Cs is de omtrek van de wapeningsstaaf.
De limiet kracht Flim is de maximale kracht in het element van de wapening, rekening houdend met de uiterste sterkte van de wapening en ook met de verankeringsomstandigheden (verbinding tussen beton en wapening en verankeringshaken, lussen, enz.)
\[F_{lim}=min\left( F_{lim,bond}+F_{au},F_{u} \right)\]
\[F_{u}=k\cdot f_{yd}\cdot A_{s}\]
\[F_{au}=\beta\cdot k\cdot f_{yd}\cdot A_{s}\]
\[F_{lim,bond}=C_{s}\cdot l \cdot f_{bd}\]
waarbij Cs de omtrek van de wapeningsstaaf is en l de lengte vanaf het begin van de wapening tot aan het punt dat van belang is.
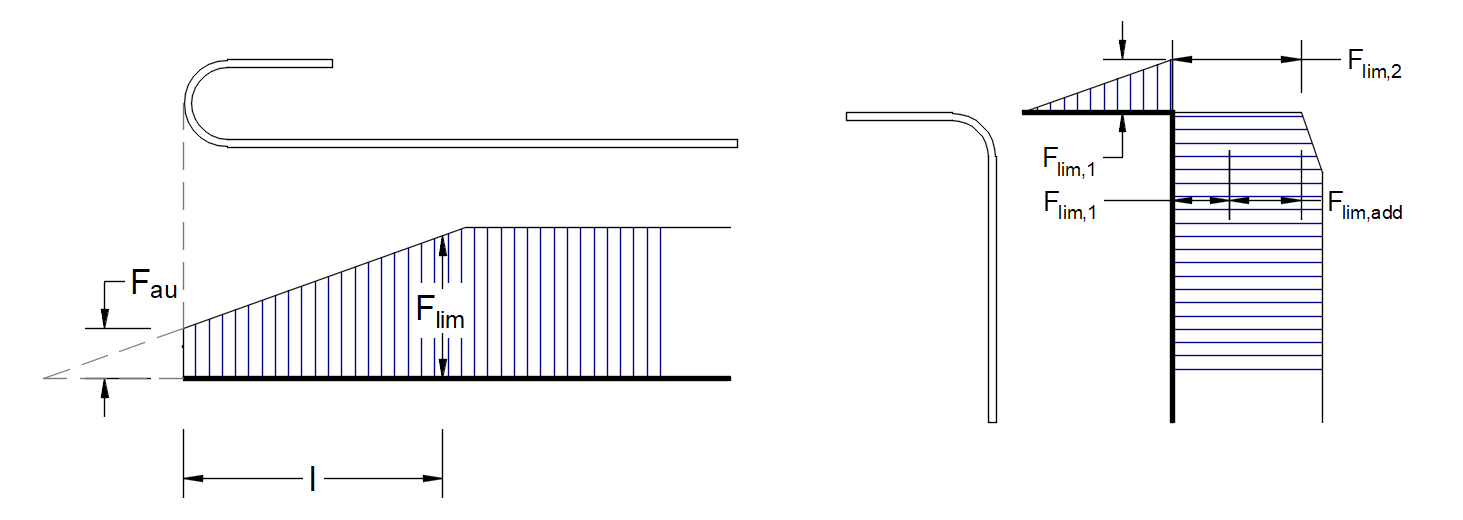
\[ \textsf{\textit{\footnotesize{Fig. 22\qquad Definitie van limiet kracht Flim}}}\]
\[F_{lim,2}=F_{lim,1}+F_{lim,add}\]
waarbijFlim,add de extra kracht is die berekend wordt uit de grootte van de hoek tussen naburige elementen.Flim,2 moet altijd lager zijn danFu.
De beschikbare verankeringstypes in 3D CSFM omvatten een rechte staaf (d.w.z. zonder reductie van het ankereinde), bocht, haak, lus, gelaste dwarsstaaf, perfecte verbinding en doorlopende staaf. Al deze types, samen met de respectievelijke verankeringscoëfficiënten β, worden getoond in Fig. 23 voor langswapening en in Fig. 24 voor beugels. De waarden van de aangenomen verankeringscoëfficiënten zijn in overeenstemming met EN 1992-1-1 paragraaf 8.4.4 Tab. 8.2. Er dient opgemerkt te worden dat ondanks de verschillende beschikbare opties, 3D CSFM drie types verankeringseinden onderscheidt: (i) geen reductie van de verankeringslengte, (ii) een reductie van 30% van de verankeringslengte in het geval van een genormaliseerde verankering en (iii) perfecte aanhechting.
\[ \textsf{\textit{\footnotesize{Fig. 23\qquad Beschikbare verankeringstypes in 3D CSFM:}}}\]
\[ \textsf{\textit{\footnotesize{(a) recht; (b) bocht; (c) haak; (d) lus; (e) gelast; (f) perfecte aanhechting; (g) doorgaande staaf.}}}\]
\[ \textsf{\textit{\footnotesize{Fig. 24\qquad Beschikbare verankeringstypes en respectievelijke verankeringscoëfficiënten voor beugels.}}}\]
\[ \textsf{\textit{\footnotesize{Gesloten beugels: (a) haak; (b) bocht; (c) overlap. Open beugels: (d) haak; (e) doorgaande staaf.}}}\]
Om te voldoen aan EN 1992-1-1, moet wapening altijd gemodelleerd worden met rechte uiteinden en moet de verankeringseigenschap gebruikt worden (een verankeringsveer moet toegepast worden). Het modelleren van de verankeringshaak door het direct wijzigen van de wapeningsgeometrie is niet in overeenstemming met EN 1992-1-1.