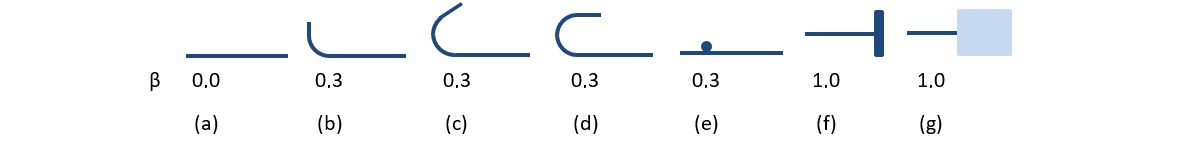Die GZT-Nachweise werden für die Betonfestigkeit, die Betonstahlfestigkeit und die Verankerung (Verbundschubspannungen) geführt.
Die Druckfestigkeit des Betons wird als Verhältnis zwischen der aus der FE-Analyse erhaltenen maximalen Vergleichsspannung σc,eq und dem Grenzwert σc,lim = fcd bewertet.
Die äquivalente Hauptspannung drückt die äquivalente einachsige Spannung für einen allgemeinen dreiachsigen Spannungszustand aus.
\[\sigma_{c,eq} = \sigma_{c3} - \sigma_{c1}\]
Der σc,eq-Wert kann daher direkt mit den Grenzwerten für die einachsige Festigkeit nach EN 1992-1-1 verglichen werden.
Dieser Ausdruck ergibt sich aus der Anwendung der Mohr-Coulomb-Plastizitätstheorie, wobei konservativ der innere Reibungswinkel φ = 0° angenommen wird .
Die Festigkeit der Bewehrung wird sowohl auf Zug als auch auf Druck als das Verhältnis zwischen der Spannung in der Bewehrung an den Rissen σsr und dem angegebenen Grenzwert σs,lim bewertet:
\(σ_{s,lim} = \frac{k \cdot f_{yk}}{γ_s}\qquad\qquad\textsf{\small{für bilineares Diagramm mit geneigtem oberen Ast}}\)
\(σ_{s,lim} = \frac{f_{yk}}{γ_s}\qquad\qquad\,\,\,\,\textsf{\small{für bilineares Diagramm mit horizontalem oberem Ast}}\)
wobei:
fyk ist die Streckgrenze der Bewehrung nach EN 1992-1-1 Cl. 3.2.3,
k ist das Verhältnis der Zugfestigkeit ftk zur Streckspannung,
\(k = \frac{f_{tk}}{f_{yk}}\)
γs ist der Teilsicherheitsbeiwert für die Bewehrung.
Die Verbundschubspannung wird unabhängig als das Verhältnis zwischen der durch FE-Analyse berechneten Verbundspannung τb und der Verbundendfestigkeit fbd gemäß EN 1992-1-1, Kap. 8.4.2:
\[\frac{τ_{b}}{f_{bd}}\le 1\]
\[f_{bd} = 2,25 \cdot η_1\cdot η_2\cdot f_{ctd}\]
wobei:
fctd ist der Bemessungswert der Betonzugfestigkeit nach EN 1992-1-1 Cl. 3.1.6 (2). Wegen der zunehmenden Sprödigkeit von höherfestem Beton ist fctk,0.05 auf den Wert von C60/75 nach EN 1992-1-1 Cl. 8.4.2 (2) begrenzt.
η1 ist ein Koeffizient, der von der Qualität des Verbundzustandes und der Lage des Stabes während des Betonierens abhängt (Abb. 31).
η1 = 1,0, wenn "gute" Bedingungen erreicht werden und
η1 = 0,7 für alle anderen Fälle und für Stäbe in Strukturelementen, die mit Gleitschalungen gebaut werden, es sei denn, es kann nachgewiesen werden, dass "gute" Verbundbedingungen bestehen
η2 bezieht sich auf den Stabdurchmesser:
η2 = 1,0 für Ø ≤ 32 mm
η2 = (132 - Ø)/100 für Ø > 32 mm
\[ \textsf{\textit{\footnotesize{Abb. 20\qquad EN 1992-1-1 Abbildung 8.2 - Beschreibung der Verbundbedingungen}}}\]
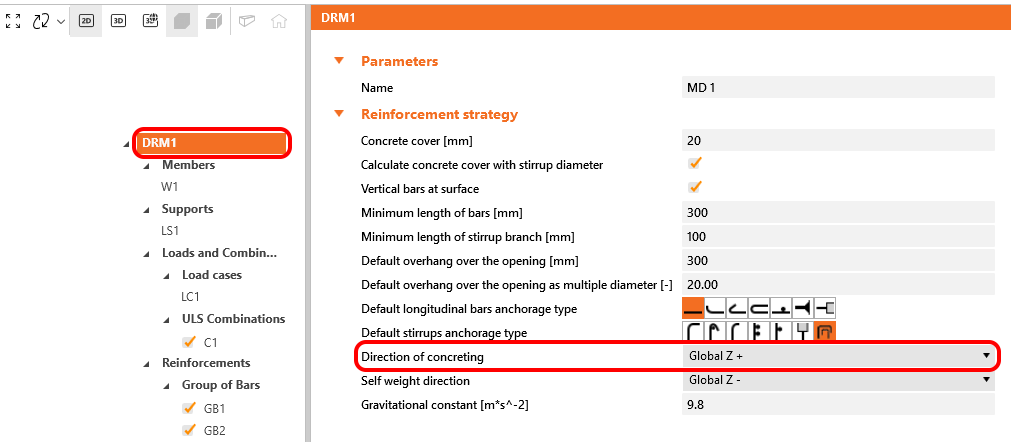
In IDEA StatiCa Detail werden die Verbundbedingungen gemäß Abb. 20 c) und d) berücksichtigt. Die Betonierrichtung kann in der Anwendung für jede Projektposition wie folgt eingestellt werden:
\[ \textsf{\textit{\footnotesize{Abb. 21\qquad Betonierrichtung}}}\]
Gesamtkraft Ftot und Grenzkraft Flim
Die Gesamtkraft Ftot ist ein Ergebnis der Finite-Elemente-Analyse und kann auf zwei Arten definiert werden.
\[F_{tot}=A_{s}\cdot \sigma_{s}\]
wobei As die Fläche des Bewehrungsstabs und σs die Spannung im Stab ist.
Oder als Summe aus der Verankerungskraft Fa und der Verbundkraft Fbond.
\[F_{tot}=F_{a}+F_{bond}\]
wobei Fa die tatsächliche Kraft in der Verankerungsfeder und Fbond die Verbundkraft ist, die durch Integration der Verbundspannung τb über die Länge des Bewehrungsstabs l ermittelt werden kann.
\[F_{bond}=C_{s} \cdot \int_{0}^{l}\tau_{b}\left( x \right)dx\]
Cs ist der Umfang des Bewehrungsstabs.
Die Grenzkraft Flim ist die minimale Kraft im Element des Bewehrungsstabs unter Berücksichtigung der Tragfähigkeit des Bewehrungsstabs und der Verankerungsbedingungen (Verbund zwischen Beton und Bewehrung und Verankerungshaken, Schlaufen usw.).
\[F_{lim}=min\left( F_{lim,bond}+F_{au},F_{u} \right)\]
\[F_{u}=k\cdot f_{yd}\cdot A_{s}\]
\[F_{au}=\beta\cdot k\cdot f_{yd}\cdot A_{s}\]
\[F_{lim,bond}=C_{s}\cdot l \cdot f_{bd}\]
wobei Cs der Umfang des Bewehrungsstabs und l die Länge vom Anfang des Bewehrungsstabs bis zum interessierenden Punkt ist.
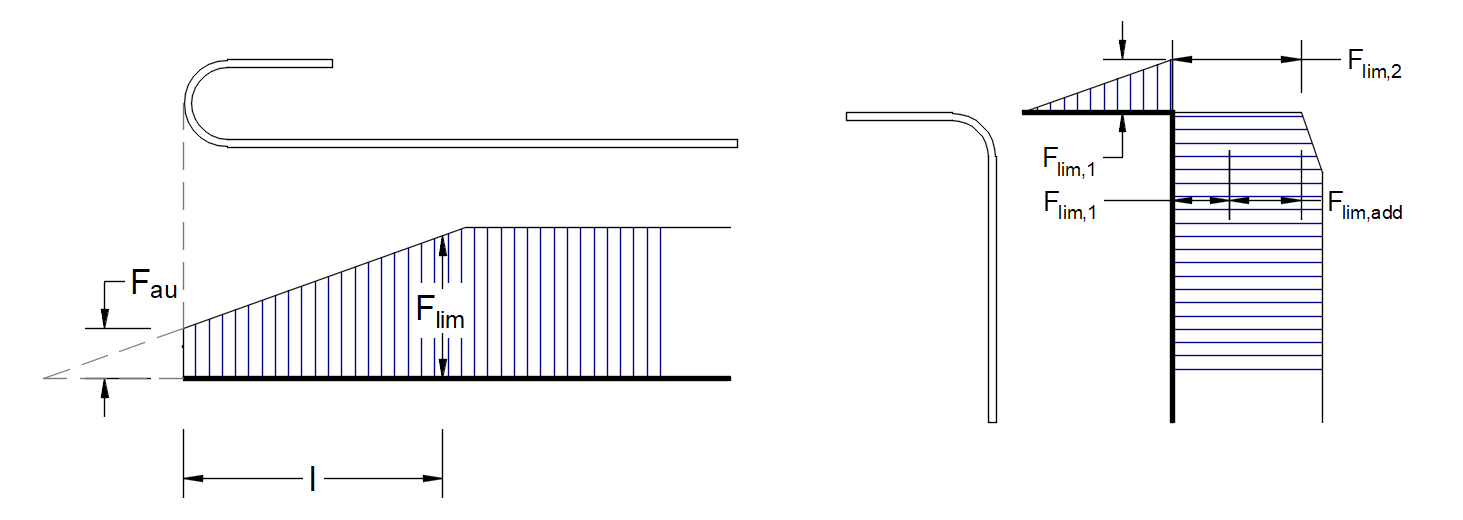
\[ \textsf{\textit{\footnotesize{Abb. 22\qquad Definition der Grenzkraft Flim}}}\]
\[F_{lim,2}=F_{lim,1}+F_{lim,add}\]
wobei Flim,add die zusätzliche Kraft ist, die aus der Größe des Winkels zwischen benachbarten Elementen berechnet wird. Flim,2 muss immer kleiner als Fu sein.
Zu den verfügbaren Verankerungstypen in 3D CSFM gehören ein gerader Stab (d.h. keine Reduzierung der Ankerenden), ein gebogener Stab, ein Haken, eine Schlaufe, ein geschweißter Querstab, ein perfekter Verbund und ein durchgehender Stab. Alle diese Typen sind zusammen mit den jeweiligen Verankerungsbeiwerten β in Abb. 23 für die Längsbewehrung und in Abb. 24 für die Bügel dargestellt. Die Werte der angenommenen Verankerungsbeiwerte entsprechen EN 1992-1-1 Abschnitt 8.4.4 Tab. 8.2. Es ist zu beachten, dass 3D CSFM trotz der verschiedenen Möglichkeiten drei Arten von Verankerungsenden unterscheidet: (i) keine Verringerung der Verankerungslänge, (ii) eine Verringerung der Verankerungslänge um 30% im Falle einer normalisierten Verankerung und (iii) perfekter Verbund.
\[ \textsf{\textit{\footnotesize{Abb. 23\qquad Verfügbare Verankerungstypen und entsprechende Verankerungsbeiwerte für Längsbewehrungsstäbe im 3D-CSFM:}}}\]
\[ \textsf{\textit{\footnotesize{(a) gerader Stab; (b) Biegung; (c) Haken; (d) Schlaufe; (e) geschweißter Querstab; (f) perfekte Verbindung; (g) durchgehender Stab}}}\]
\[ \textsf{\textit{\footnotesize{Abb. 24\qquad Verfügbare Verankerungstypen und entsprechende Verankerungsbeiwerte für Bügel.}}}\]
\[ \textsf{\textit{\footnotesize{Geschlossene Steigbügel: (a) Haken; (b) Biegung; (c) Überlappung. Offene Steigbügel: (d) Haken; (e) durchgehender Stab}}}\]
Um die Anforderungen von EN 1992-1-1 zu erfüllen, sollte die Verankerungsfeder in der Berechnung verwendet werden. Die Verankerungsfeder wird durch den Beiwert β modifiziert, so dass der Benutzer bei der Definition der Anfangs- und Endbedingungen der Bewehrung eine der verfügbaren Verankerungsarten verwenden muss.