Steel joint buckling analysis
Buckling is usually not an important issue in joints. However, it should be checked that there are no buckling issues and that the results of strength analysis, which uses only geometrically linear analysis, are correct.
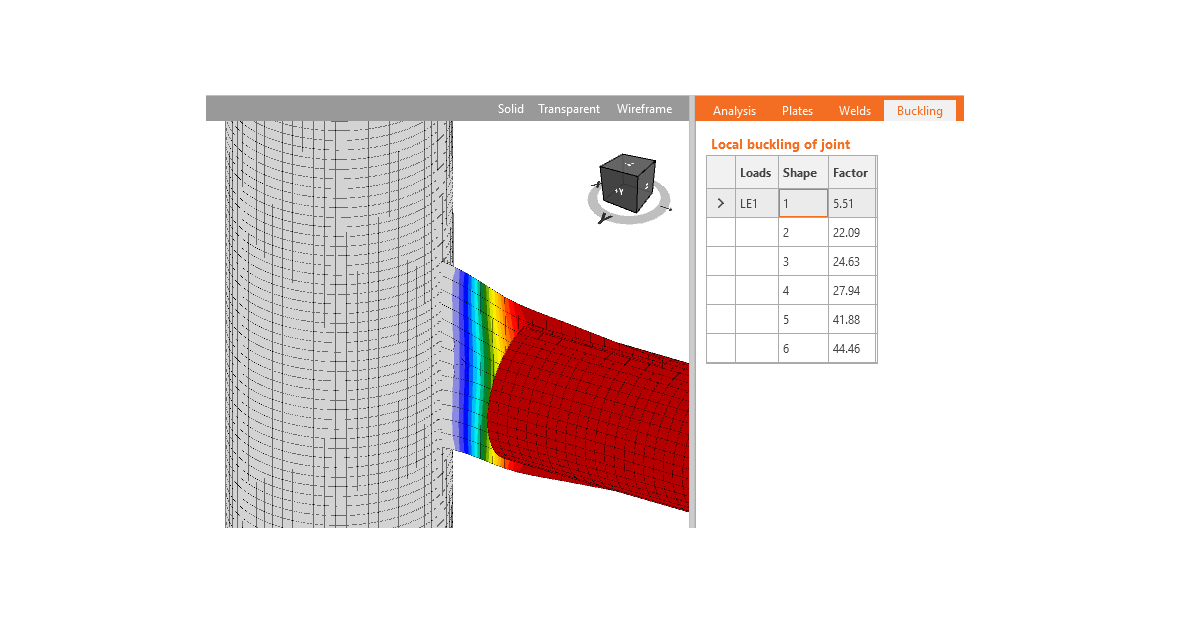
IDEA StatiCa Connection can perform linear buckling analysis of a model of a joint. The results are predicted in buckling modes. Critical load, at which buckling of the perfect model occurs, is calculated for each buckling mode. Critical load is presented by multipliers of the load acting on the joint. According to the buckling mode and critical load multiplier, the user can determine the safe buckling design.
Some codes, e.g. Eurocode (EN 1993-1-1, Chapter 5.2.1), recommend a critical load multiplier higher than 15 for bar models of structures. If the critical load multiplier is higher than 15, the code does not require a buckling check of members.
For joints, the matter is different, and the code does not provide any specific recommendation. The design of local buckling must be tackled in another way. Generally, the local buckling may be divided into three groups:
- Plates connecting individual members
- Stiffening plates in the joint – stiffeners, ribs, short haunches
- Closed sections and thin-walled sections
The buckling of plates from group 1 affects the buckling shape of the whole member. Therefore, it is recommended to apply the same rules as for these members also to these plates, i.e., consider safe critical load multiplier 15 and higher. The engineer should verify that the real execution of the joint corresponds to the boundary conditions of the model used for buckling analysis of the whole structure.
Plates from group 2 affect the local buckling of the joint. For such plates, the safe boundary of critical load multiplier 15 is conservative, but specific guidance is missing in codes. The guidance is provided by research papers that recommend a safe boundary of critical load multiplier equal to 3.
Buckling of plates and members from group 3 is very problematic, and individual assessment of each particular case is necessary.
For plates with a critical load multiplier smaller than suggested values (15 for group 1, 3 for group 2), plastic design cannot be used. Other methods that are not offered by IDEA StatiCa are necessary for their check.
The result of buckling analysis in IDEA StatiCa Connection is not a definite check. The codes do not give sufficient guidance. The assessment requires engineering judgment and IDEA StatiCa provides unique tools not available in standard design software.
Gusset plate as an elongation of a truss – example of the plate from group 1 for which buckling can be neglected if the critical buckling factor is higher than 15
Examples of buckling shapes of plates from group 2 where the buckling can be neglected if the critical buckling factor is higher than 3
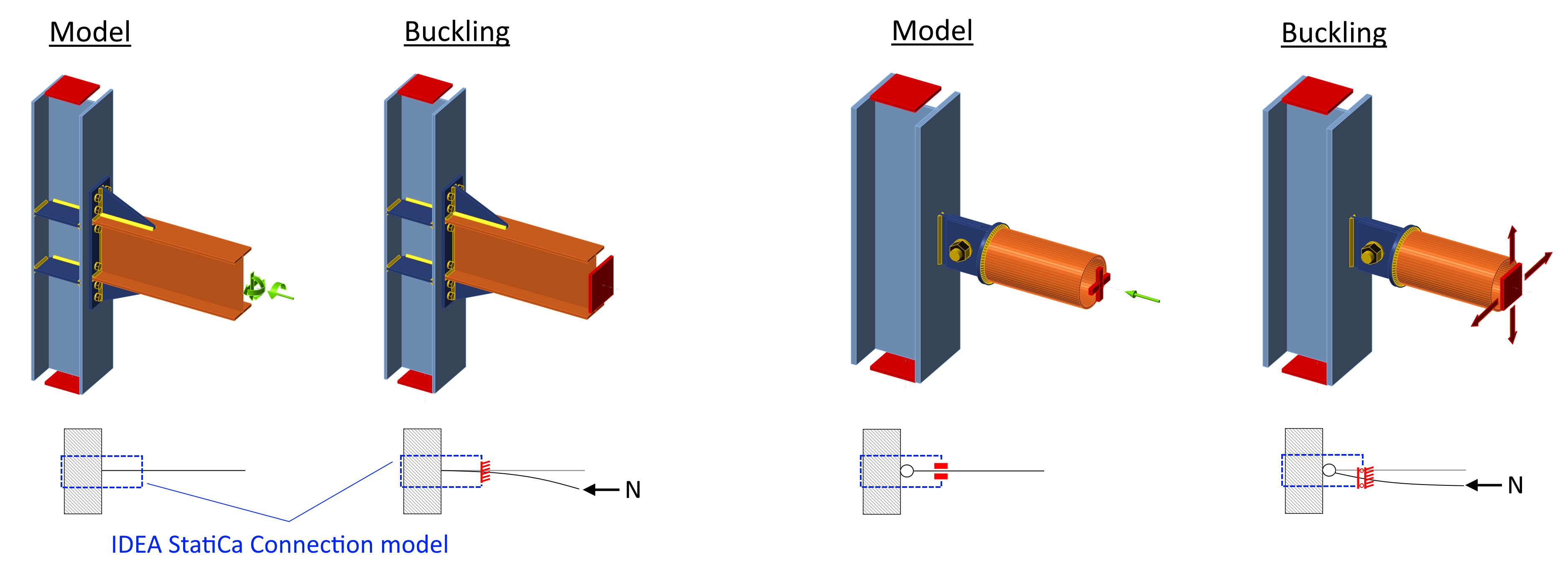
The model used for buckling analysis is supported by different supports than set by the user in stress, strain analysis type (EPS). The bearing member stays fully supported. Model type of a beam set as N-Vy-Vz-Mx-My-Mz (free to move in stress, strain analysis type) is fully supported in buckling analysis. All other beam analysis types have restrained bending moments and normal force but are free to move sideways.
- Model type N-Vy-Vz-Mx-My-Mz: supports in buckling model: N-Vy-Vz-Mx-My-Mz
- Model type N-Vy-Vz: supports in buckling model: N-Mx-My-Mz
- Model type N-Vz-My: supports in buckling model: N-Mx-My-Mz
- Model type N-Vy-Mz: supports in buckling model: N-Mx-My-Mz
It is assumed that in case of rigid joint, user sets the bending moment and the buckling of the short beam segment is not relevant. On the other hand, in the case of the pinned joint, user sets only normal and shear force and no bending moment, but the buckling of the pinned member is relevant, so it contributes to the buckling factor. See the figure below. "Model" shows the model in the stress-strain analysis type, and "Buckling" shows the model in the buckling analysis.