Beton unterhalb der Fußplatte wird vom Winkler-Untergrund mit gleichmäßiger Steifigkeit simuliert, die die Kontaktspannungen liefert. Für den Drucknachweis wird die nach EN 1993-1-8 ermittelte mittlere Spannung an der wirksamen Fläche verwendet.
Die Tragfähigkeit von Beton bei räumlichem Druck wird in Anlehnung an EN 1993-1-8 durch Berechnung der Bemessungstragfähigkeit des Betons im Anschluss fjd unter der wirksamen Fläche Aeff der Fußplatte ermittelt. Die Bemessungstragfähigkeit des Anschlusses fjd wird nach Abs. 6.2.5 in EN 1993-1-8 und Abs. 6.7 in EN 1992-1-1 ermittelt. Die Qualität und Dicke des Mörtels wird durch den Fugenbeiwert βjd bestimmt. Für eine Mörtelqualität gleich oder besser als die Qualität des Betonblocks wird βjd = 1,0 angenommen, EN 1993-1-8 empfiehlt den Wert βjd = 0,67. Die wirksame Fläche Aeff,cm unter der Fußplatte wird als die Form des Stützenquerschnitts, vergrößert um zusätzliche Ausbreitungsbreite c, ermittelt.
\[ c = t \sqrt{\frac{f_y}{3 f_{jd} \gamma_{M0}}} \]
mit t als Dicke der Fußplatte, fy der Streckgrenze der Fußplatte und γM0 als Teilsicherheitsbeiwert für Stahl.
Die wirksame Fläche wird durch Iteration berechnet, bis die Differenz zwischen den zusätzlichen Ausbreitungsbreiten der aktuellen und vorherigen Iteration |ci – ci–1 | weniger als 1 mm beträgt. Für die erste Iteration wird die Fläche der Fußplatte als tragende Fläche Ac0 angenommen.
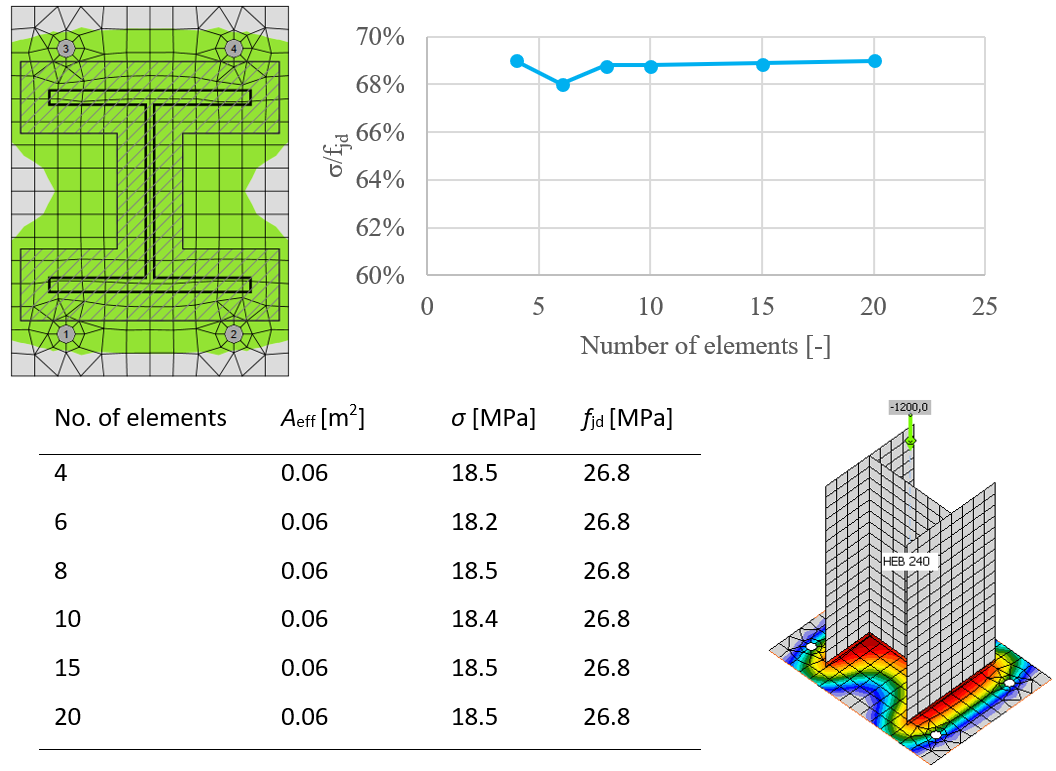
Die Fläche, in der der Beton unter Druck steht, wird den Ergebnissen der FEM entnommen. Diese aus Druck belastete Fläche Aeff,FEM ermöglicht das Ermitteln der Position der neutralen Achse. Der Nutzer kann diese Fläche ändern, indem er in den Normeinstellungen „Wirksamer Bereich – Einfluss der Netzgröße“ bearbeitet. Der Standardwert ist 0,1, für den die Verifizierungsstudien durchgeführt wurden. Es wird nicht empfohlen, diesen Wert zu verringern. Eine Erhöhung dieses Wertes macht die Beurteilung der Betontragfähigkeit sicherer. Der Wert in den Normeinstellungen bestimmt die Grenze des Bereichs, Aeff,FEM, z.B. berücksichtigt der Wert von 0,1 nur Bereiche, in denen die Betonspannung größer ist als das 0,1-fache der maximalen Betonspannung, σc,max. Der Schnittpunkt der Druckfläche Aeff,FEM und der wirksamen Fläche Aeff,cm ermöglicht die Bewertung der Tragfähigkeit für eine allgemein belastete Fußplatten jeder Form mit beliebigen Versteifungen und wird mit Aeff bezeichnet. Die durchschnittliche Spannung σ auf der wirksamen Fläche, Aeff, wird als Druckkraft dividiert durch die wirksame Fläche bestimmt. Nachweis des Bauteils auf Spannungen mit σ ≤ fjd.
Betontragfähigkeit bei konzentriertem Druck:
\[ f_{jd}= \beta_j k_j \frac{f_{ck}}{\gamma_c} \]
Konzentrationsfaktor unter Berücksichtigung der Erhöhung der Betondruckfestigkeit durch mehraxiale Spannung:
\[ k_j=\sqrt{\frac{A_{c1}}{A_{eff}}} \le 3,0 \]
mit Ac1 nach EN 1992-1-1 – Abs. 6.7. Die Fläche muss konzentrisch und geometrisch ähnlich der tragenden Fläche Aeff sein.
Durchschnittliche Spannung unter der Fußplatte:
\[ \sigma = \frac{N}{A_{eff}} \]
Ausnutzung bei Druck [%]:
\[ Ut = \frac{\sigma}{f_{jd}} \]
Wo:
- fck – Charakteristische Druckbetonfestigkeit
- βj = 0,67 – Faktor der Mörtelqualität, änderbar in den Normeinstellungen
- γc – Sicherheitsfaktor für Beton
- Aeff – Wirksame Fläche, auf die sich die Normalkraft N verteilt
Die wirksame Fläche, Aeff,cm, berechnet nach EN für reinen Druck, ist mit einer gestrichelten Linie markiert. Die grafische Darstellung zeigt die Art der Überprüfung. Die berechnete wirksame Fläche Aeff,fem ist grün markiert. Die endgültige wirksame Fläche, Aeff, für den Nachweis der Kontaktspannung ist schraffiert hervorgehoben.
In seltenen Fällen, insbesondere bei nur durch Zugkraft belasteten Fußplatten (Druck im Beton wird durch Abstützkräfte verursacht) oder Zugkraft und Biegemoment, ist der Schnittpunkt der Flächen Aeff,cm und Aeff,fem sehr klein oder gar nicht vorhanden. In solchen Fällen sind die Druckkräfte im Allgemeinen sehr klein, der Nachweis liegt außerhalb des Geltungsbereichs des Eurocodes und der Beton unter Druck wird nicht nachgewiesen.
Netzsensitivität
Dieses Verfahren zur Beurteilung der Druckfestigkeit des Betons ist unabhängig vom Netz der Fußplatte, wie in den folgenden Abbildungen zu sehen ist. Sie wird am Beispiel von Beton in der Druckbemessung nach EN gezeigt. Es wurden zwei Fälle untersucht: Belastung durch reinen Druck von 1200 kN und Belastung durch eine Kombination von Druckkraft 1200 kN und Biegemoment 90 kN.
Einfluss der Anzahl der Elemente auf die Vorhersage des Drucktragfähigkeit des Betons bei reinem Druck
Der Einfluss der Anzahl der Elemente auf die Vorhersage die Tragfähigkeit des Betons unter Druck bei Druck und Biegung
Schub im Betonblock
Schub in Betonblock kann auf eine der drei Arten übertragen werden:
- Reibung
\( Ut = \frac{V}{V_{Rd}} \)
Vrd = N * Cf
- Scherlasche
\( Ut = \max \left ( \frac{V_y}{V_{Rd,y}}, \, \frac{V_z}{V_{Rd,z}}, \, \frac{V}{V_{c,Rd}} \right ) \) \(V_{Rd,y} = \frac{A_{Vy} f_y}{\sqrt{3} \gamma_{M0}} \)
\( V_{Rd,z} = \frac{A_{Vz} f_y}{\sqrt{3} \gamma_{M0}} \)
\( V_{c,Rd} = A \sigma_{Rd,max} \)
Profildübel und Schweißnähte werden ebenfalls durch die FEM überprüft.
- Anker
Der Nachweis erfolgt gemäß ETAG 001 - Anhang C
Wo:
- AV,y, AV,z – Scherflächen des Querschnitts der Scherlasche in Richtung der Achsen y und z
- fy – Streckgrenze
- γM0 – Sicherheitsfaktor
- Vy – Scherkraftkomponente in der Ebene der Fußplatte in y-Achsrichtung
- Vz – Scherkraftkomponente in der Ebene der Fußplatte in z-Achsrichtung
- V – Scherkraft (Vektorsumme beider Scherkraftkomponenten)
- N – Kraft senkrecht zur Fußplatte
- Cf – Reibungskoeffizient zwischen Stahl und Beton/Mörtel; änderbar in den Normeinstellungen
- A = l * b – Projizierte Fläche der Scherlasche ohne den Bereich über der Betonoberfläche
- l – Länge der Scherlasche ohne den Bereich über der Betonoberfläche
- b – Projizierte Breite der Scherlasche in Richtung der Schubbelastung
- σRd,max = k1 * v' * fcd – Maximale Spannung, die an den Kanten des Knotens aufgebracht werden kann
- k1 = 1 – Faktor (EN 1992-1-1 – Gleichung (6.60))
- v' = 1 – fck / 250 – Faktor (EN 1992-1-1 – Gleichung (6.57N))
- \( f_{cd} = \alpha_{cc} \frac{f_{ck}} {\gamma_c} \) – Bemessungsdruckfestigkeit des Betons
- αcc – Koeffizient für Langzeitwirkungen auf die Druckfestigkeit von Beton
- fck – Charakteristische Druckfestigkeit des Betons
- γc – Sicherheitsfaktor für Beton