Leermodule: Belastingspad en faalwijzen van een stijve verbinding (EN)
IDEA StatiCa maakt gebruik van een niet-lineair analysemodel en heeft een gebruiksvriendelijke interface met een 3D-weergave van resultaten (vervorming, spanning, plastische rek) en is dus zeer geschikt voor het onderzoeken van het gedrag van staalverbindingen.
Voortbouwend op deze sterke punten is een reeks oefeningen opgesteld, waarin IDEA StatiCa dient als virtueel laboratorium om studenten inzicht te geven in het gedrag en ontwerp van staalverbindingen. Deze leermodules zijn in de eerste plaats bedoeld voor gevorderde bachelor- en masterstudenten, maar zijn ook geschikt voor praktijk ingenieurs. De leermodules werden ontwikkeld door Associate Professor Mark D. Denavit van de University of Tennessee, Knoxville. Deze leermodule is afgeleid van de leermodule: Load Path and Failure Modes of Fully Restrained Moment Connections (AISC) en aangepast voor Eurocode door assistent professor Martin Vild van de Technische Universiteit van Brno.
Leerdoel
Na het voltooien van deze module is de lezer in staat het belastingspad van een stijve verbinding te beschrijven en de relevante faalwijzen te identificeren.
Volg het pad van de belasting
Belastingen die op een constructie worden uitgeoefend, worden via staven en verbindingen overgedragen voordat ze uiteindelijk worden opgenomen door de fundering. Het volgen van het pad van de belasting, vanaf het punt van inwerking tot aan de fundering, is een nuttige kwalitatieve oefening om te controleren of het lastpad ononderbroken is en of elk onderdeel voldoende stijfheid en sterkte heeft. Het volgen van een deel van dit pad door een verbinding biedt dezelfde voordelen.
Bij traditioneel verbindingontwerp helpen belastingspaden ingenieurs om een lijst van controlepunten op te stellen en na te gaan of elke stap in het pad voldoende stijfheid en sterkte heeft. Bij ontwerpen op basis van inelastische analyse geven belastingspaden inzicht in het gedrag van de verbinding, waarmee de resultaten van numerieke analyses kunnen worden beoordeeld.
Momentverbindingen
Een van de belangrijkste classificaties van verbindingen is gebaseerd op hun rotatiestijfheid. Eenvoudige dwarskrachtverbindingen zijn voldoende soepel om aan te nemen dat er geen moment wordt overgedragen. Momentvaste verbindingen daarentegen dragen wél een moment over tussen ligger en kolom. Volledig stijve verbindingen zijn zo stijf dat er geen relatieve rotatie optreedt tussen de staven.
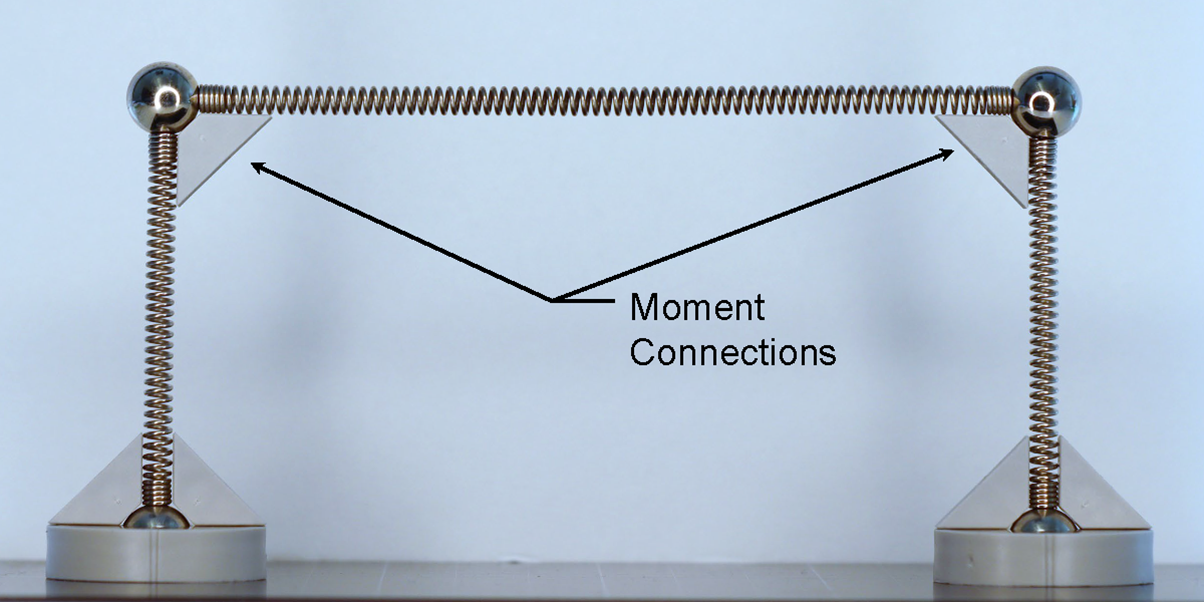
Gedemonstreerd moment-frame met onderdelen uit een Mola bouwpakket
Aangezien het grootste deel van het moment in een I-profiel wordt opgenomen door de flenzen, moeten momentvaste verbindingen rechtstreeks op deze flenzen aangrijpen. Meestal dragen momentverbindingen ook afschuif- of andere krachten van de ligger over op de kolom. Daarom grijpen ze doorgaans ook rechtstreeks aan op het lijf van de ligger. Hierdoor zijn momentverbindingen in de regel statisch onbepaald, en de werkelijke spanningsverdeling in de verbinding hangt af van de relatieve stijfheid van de verschillende onderdelen.
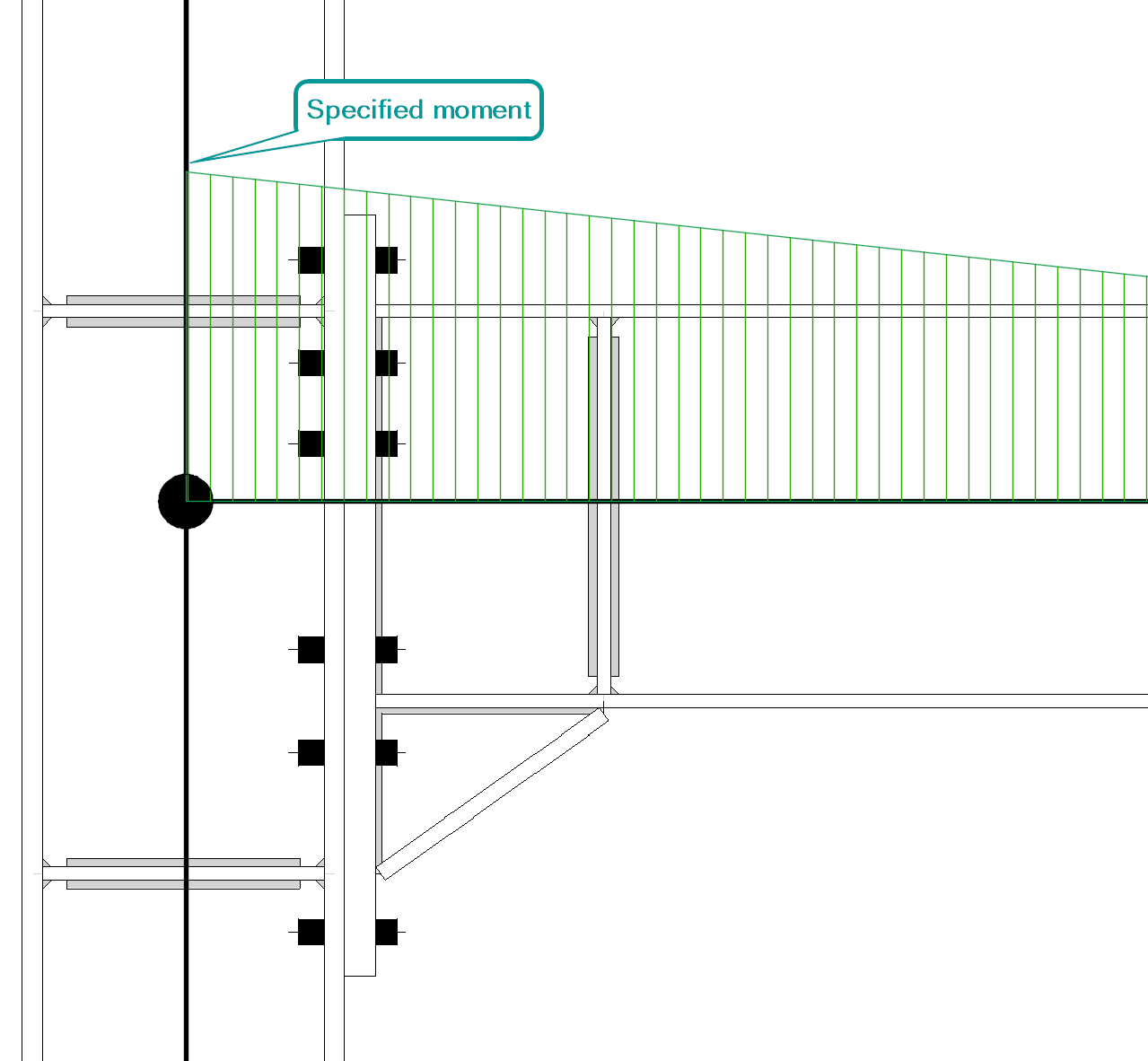
Afschuifkrachten zorgen voor een momentverloop in de ligger. Bij momentverbindingen die zich over een bepaalde lengte van de ligger uitstrekken, is het moment dus niet constant. In handberekeningen wordt dit momentverloop vaak conservatief verwaarloosd en wordt uitgegaan van één enkele momentwaarde, ongeacht de lengte van de verbinding. In IDEA StatiCa kan dat niet, omdat de analyse het evenwicht bewaart en het momentverloop dus correct gedefinieerd moet worden, in overeenstemming met de globale analyse. Het opgegeven moment wordt toegepast op de locatie die is ingesteld via de optie “Forces in” in het staafmenu.
De verbinding die we gaan analyseren
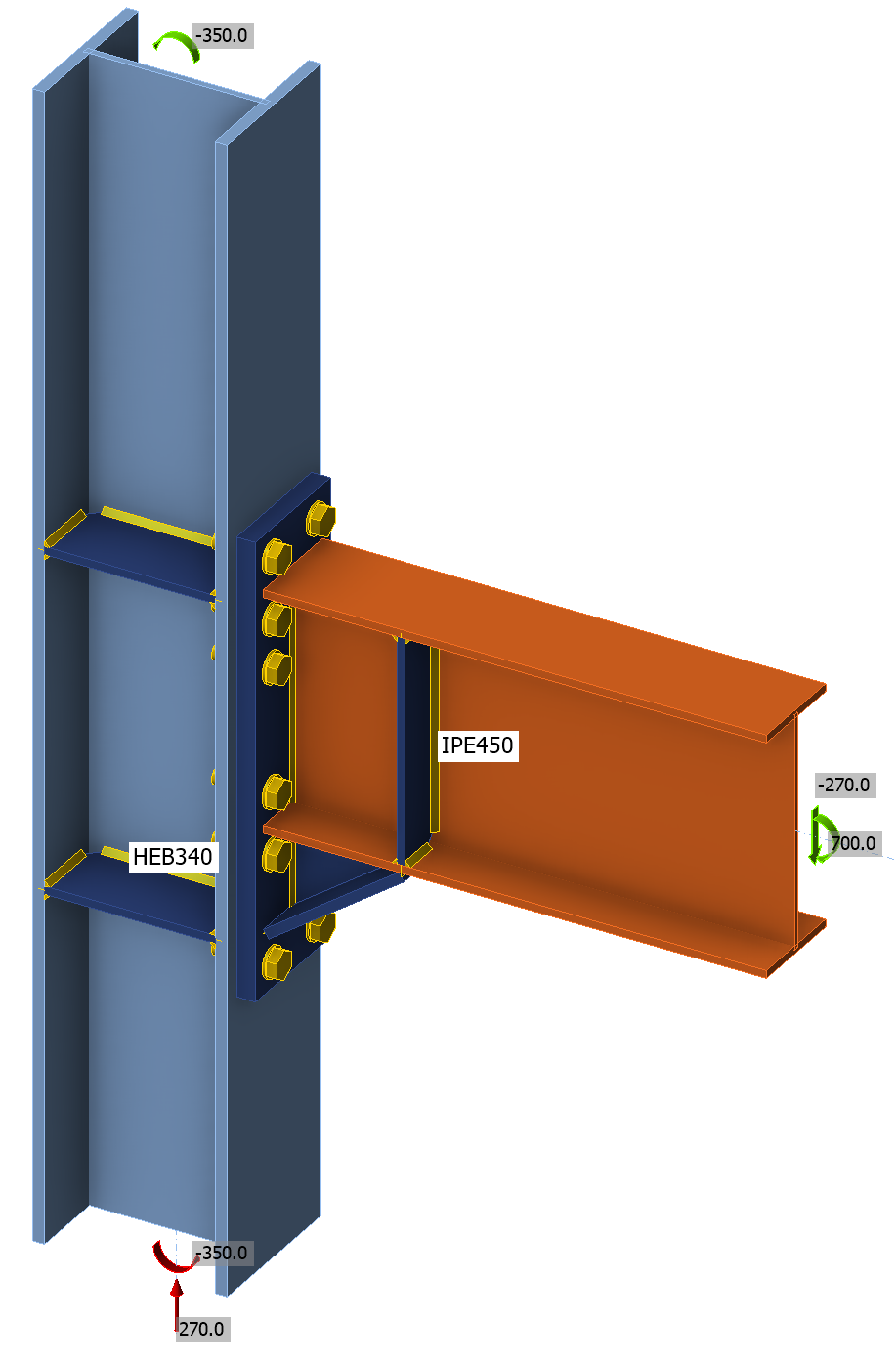
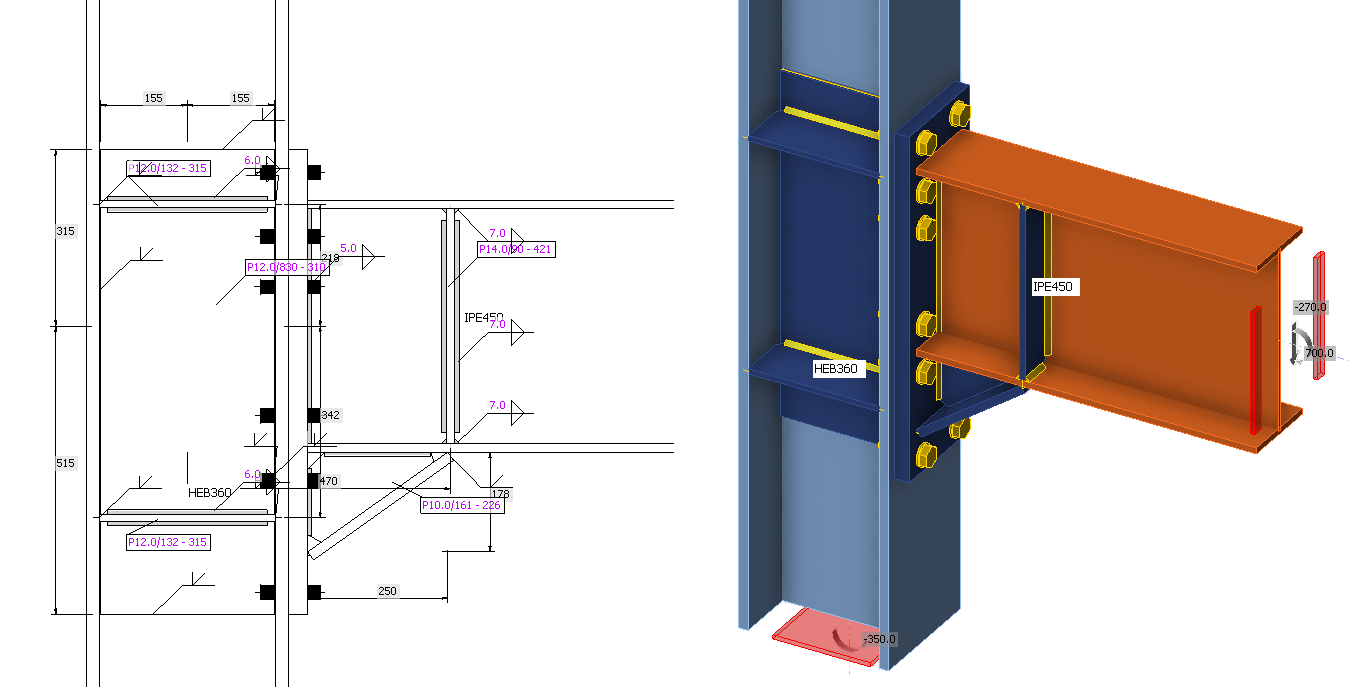
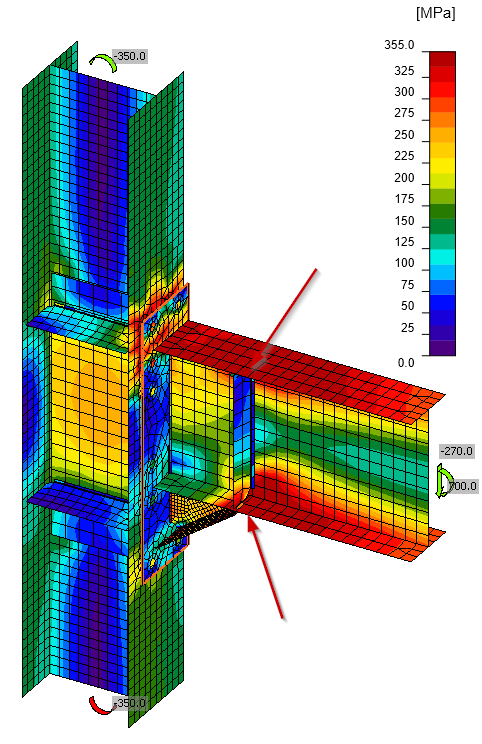
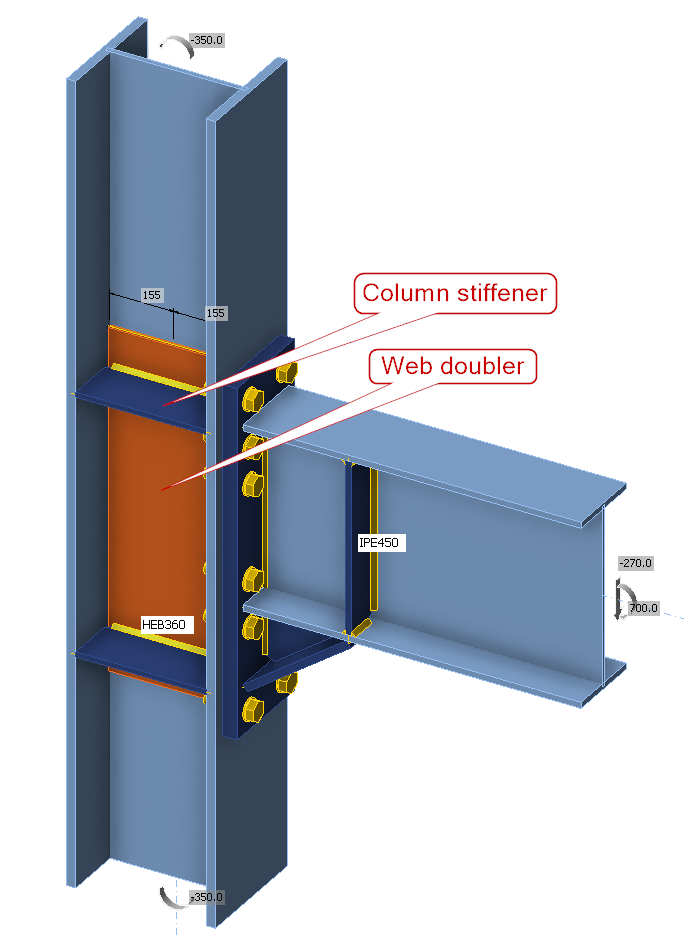
De onderzochte verbinding is geïnspireerd op het Equaljoints project. De verbinding die we gaan bekijken is een momentverbinding, verstevigd met een console (haunch) en verstijvers in de kolom en ligger.
De verbinding wordt belast met een dwarskracht van Vz = 270 kN en een buigend moment van My = 700 kNm. De belastingen zijn gespecificeerd in het knooppunt.
Deze leermodule gaat ervan uit dat de lezer vertrouwd is met het gebruik van IDEA StatiCa, zoals het navigeren door de software, definiëren van bewerkingen, uitvoeren van berekeningen en het analyseren van resultaten.
Download en open het IDEA StatiCa model. Volg vervolgens de uitleg, voer de opdrachten uit en beantwoord de vragen om de leermodule te voltooien.
Belastingspad
Het belastingspad voor afschuiving van de ligger naar de kolom is als volgt:
- De afschuiving concentreert zich in het lijf van de ligger.
- De afschuifspanningen stromen door de lassen naar de kopplaat.
- Via de kopplaat wordt de belasting verdeeld over de bouten.
- Via afschuiving in de bouten wordt de dwarskracht overgebracht naar de kolomflens en vervolgens door normaalkracht in de kolom naar de fundering.
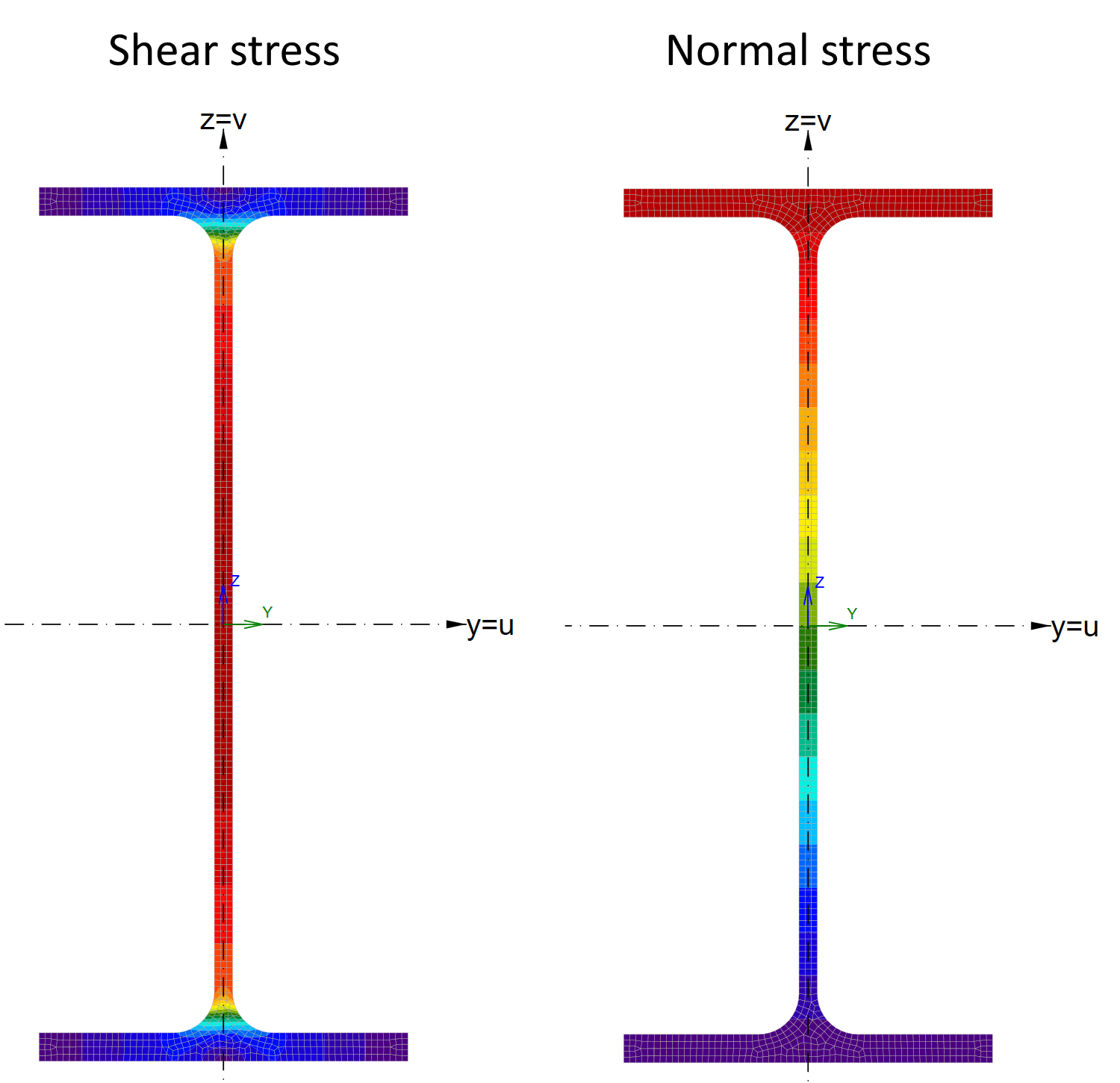
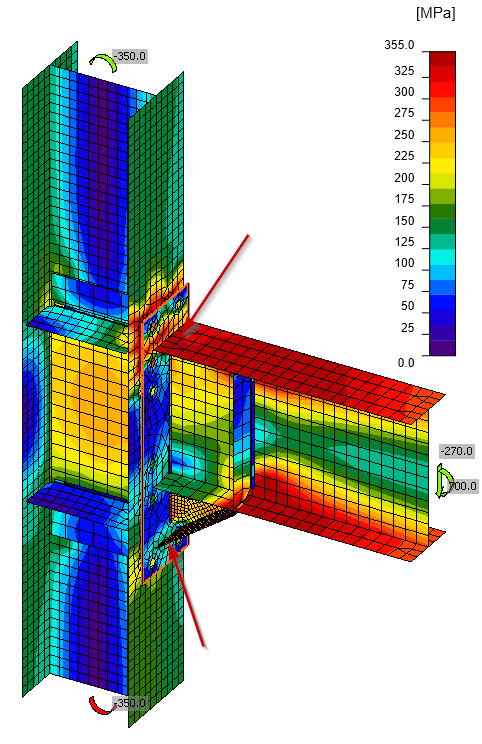
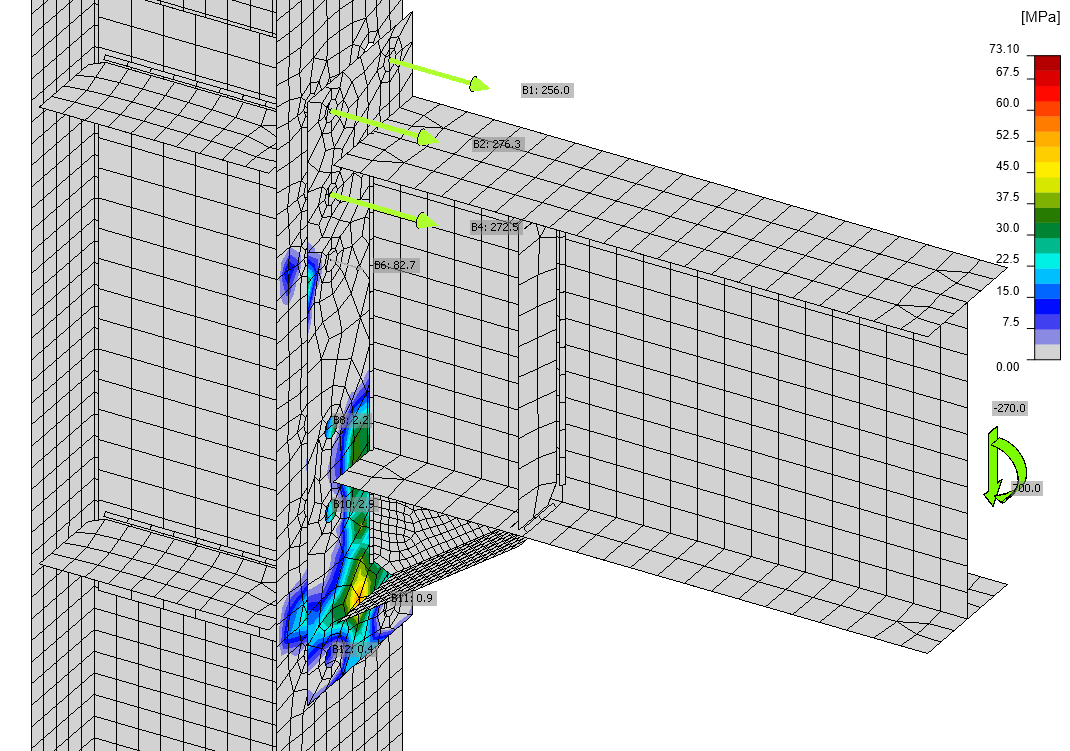
Schuifspanningen veroorzaakt door dwarskracht en normaalspanningen veroorzaakt door buigmoment bij elastische fase
Het belastingspad voor het buigend moment van de ligger naar de kolom is als volgt:
- Het moment concentreert zich voornamelijk in de flenzen van de ligger, die daardoor onder trek en druk komen te staan.
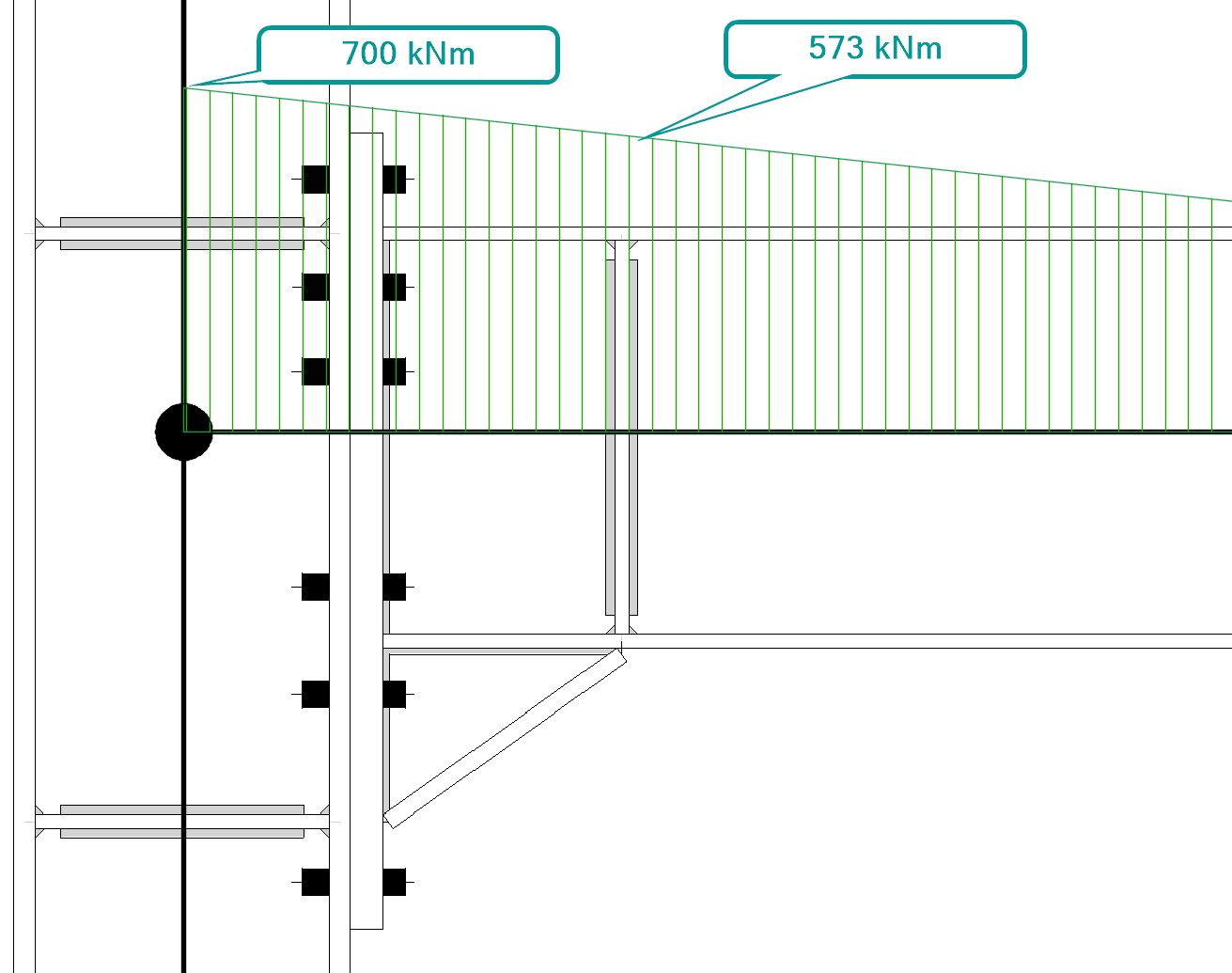
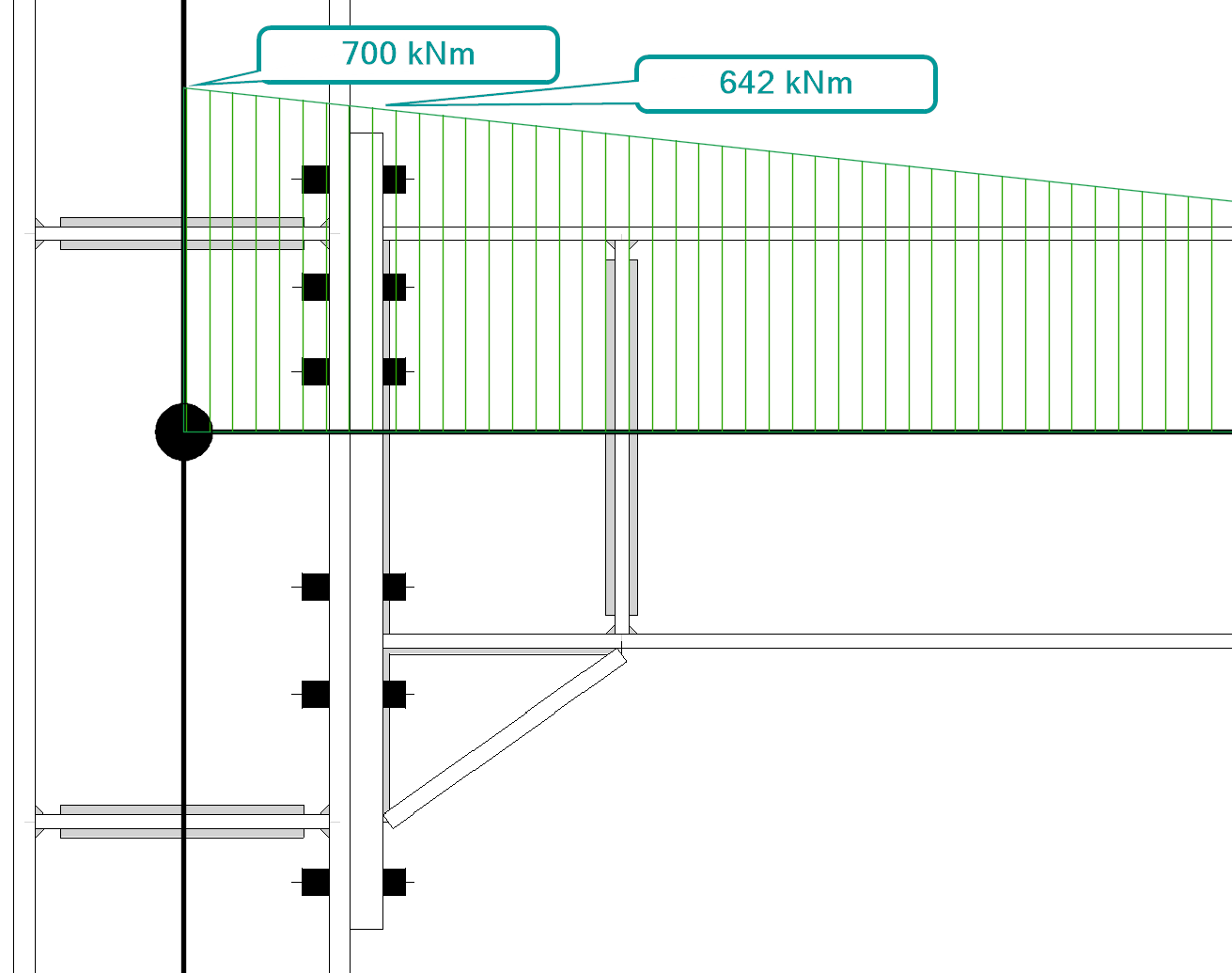
- De console is toegevoegd om de hefboomarm en daarmee de momentweerstand te vergroten. Het buigend moment is het grootst in de knoop en neemt dankzij de afschuifkracht geleidelijk af. De spanningen als gevolg van het buigend moment verlopen voornamelijk via de bovenflens en de flens van de console.
- Vanuit de ligger en de console wordt de belasting via lassen overgedragen op de kopplaat.
- Het buigend moment wordt overgedragen via de hefboomwerking van twee krachten: trek via de boutkrachten in de boutrijen nabij de bovenflens, en druk via contact tussen de kopplaat en de kolomflens.
- Kolomverstijvers vergroten de sterkte en stijfheid van de kolom tegen geconcentreerde belastingen op de plekken waar deze het grootst zijn – bij de bovenflens van de ligger en de onderflens van de console.
- De belasting uit de kopplaatbouten en de lassen van de verstijvers verspreidt zich door de kolomdoorsnede, wat resulteert in afschuif in de panel zone en een buigend moment in de kolom.
Ligger
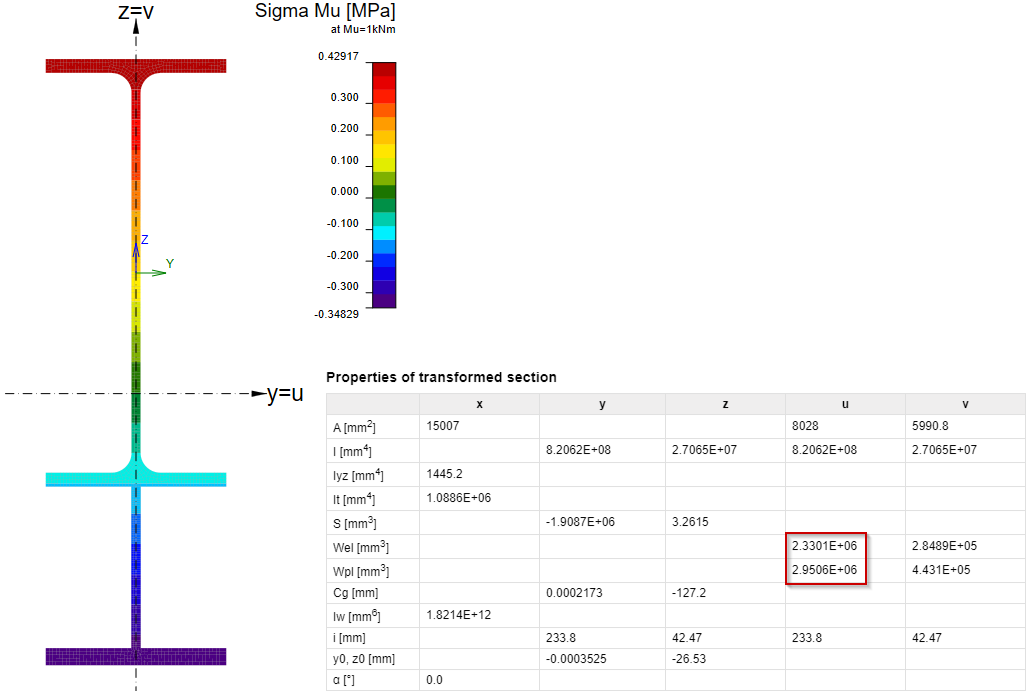
De ligger wordt belast met een moment, daarom moeten faalwijzen zoals plastisch bezwijken bij buiging en globale instabiliteit worden onderzocht als onderdeel van de staafcontrole. De globale stabiliteit kan in IDEA StatiCa Member worden gecontroleerd. Buiging met plastisch bezwijken wordt in IDEA StatiCa Connection getoetst aan de grens van 5% plastische rek. Het meest kritieke punt bevindt zich aan het uiteinde van de console.
De afstand tot het begin van de console is:
\[ h_c/2+t_p+b_h = 360/2+35+255 = 470 \textrm{ mm} \]
En het buigend moment:
\[ M_{Ed} + 0,470 \cdot V_{Ed} = 700 + 0,470 \cdot (-270) = 573,1 \textrm{ kNm} \]
De spanning in de balk kan worden berekend met behulp van het elastisch of plastisch weerstandsmoment. Door gebruik te maken van het elastisch weerstandsmoment verkrijgen we:
\[ M_{Ed} / W_{el,y} = 573,1 \cdot 10^6/ 1,5 \cdot 10^6 = 382 \textrm{ MPa} \]
Dit is hoger dan de vloeigrens, wat betekent dat de flenzen al moeten bezwijken.
Op basis van het plastisch weerstandsmoment:
\[ M_{Ed} / W_{pl,y} = 573,1 \cdot 10^6/ 1,7 \cdot 10^6 = 337 \textrm{ MPa} \]
Dit is onder de vloeigrens. De doorsnede is aan het buigen maar nog niet volledig geplastificeerd. We kunnen 355 MPa verwachten bij de flenzen en een elasto-plastische spanningsverdeling in het lijf.
Merk op dat de eenassige langsspanning gelijk is aan de equivalente spanning die IDEA StatiCa laat zien. De spanningen bevestigen onze berekeningen.
Console
De console (haunch) vergroot de doorsnede van de ligger. Hierdoor wordt de hefboomsarm tussen de trekkrachten in de bouten en het drukpunt in de onderflens groter en nemen de sterkte en stijfheid van de verbinding toe.
Het buigend moment tussen de kopplaat en de console is:
\[ M_{Ed} + (h_c/2+t_p) \cdot V_{Ed} = 700 + (0.36/2+0.035) \cdot (-270) = 642 \textrm{ kNm}\]
De exacte berekening van het weerstandsmoment van een ligger met console is relatief ingewikkeld. In een vereenvoudigde berekening kunnen we de onderste flens van de ligger verwaarlozen en aannemen dat de dikte van het lijf en de flens van de haunch gelijk is aan de dikte van het lijf en de flens van de ligger.
\[W_{pl,y} = 2 \cdot [(14.6 \cdot 190) \cdot (450+178)/2 +(450+178)/2 \cdot (450+178)/4)] = 1 840 668 \textrm{ mm}^3 \]
De spanning rond de flens aan het uiteinde van de console is:
\[ \sigma = M_{Ed}/W_{pl,y} = 642 \cdot 10^6 / 1840668 = 349 \textrm{ MPa}\]
Ook hier zullen we plastische rekken verwachten in de flenzen. Dit komt overeen met IDEA StatiCa.
De algemene doorsnede-editor van IDEA StatiCa kan helpen om het weerstandsmoment van complexere doorsnedes exact te berekenen.
Kopplaat
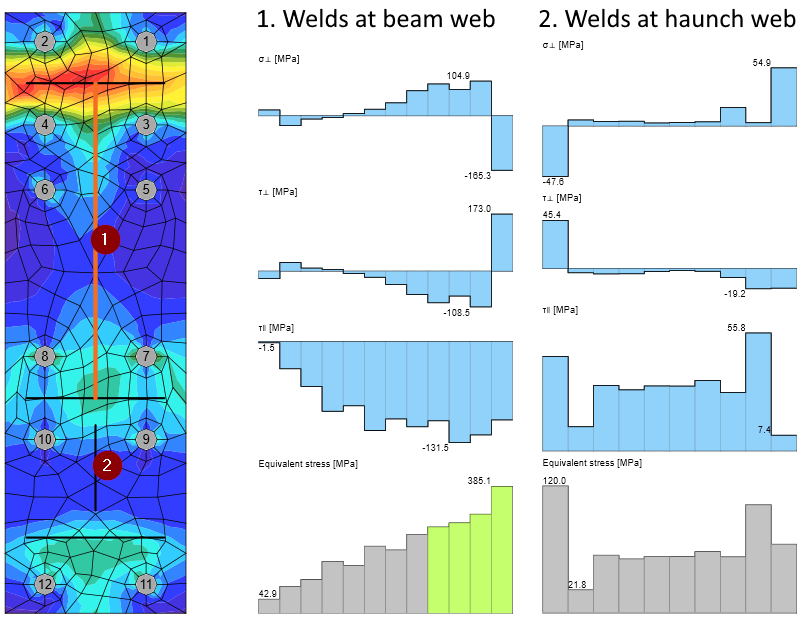
De afschuif- en normaalspanningen worden via lassen overgebracht naar de kopplaat. Lassen met volledige doorlassing worden gebruikt voor kritische lassen van flenzen. Een dubbele hoeklas wordt gebruikt bij het lijf waar de lassen minder belast worden.
Er zijn verschillende benaderingen die we kunnen gebruiken voor het ontwerpen van lassen op I-profielen.
- De meest eenvoudige is aan te nemen dat lassen bij flenzen buigmomenten opnemen en lassen bij het lijf afschuifkracht overbrengen.
- Nauwkeuriger in het elastische stadium is de aanname dat de lasgroep het buigmoment overdraagt in verhouding tot het traagheidsmoment, d.w.z.:
\[ M_{flens} = I_{flens}/I_{totaal} \]
\[ M_{lijf} = I_{lijf}/I_{totaal} \]
waarbij:
- Mflens - deel van het buigmoment overgedragen via flenslassen
- Mlijf - deel van het buigmoment dat wordt overgebracht via lassen in het lijf
- Merk op dat \( M_{flens}+M_{lijf} = M_{totaal} \)
- Iflens - traagheidsmoment van flenzen
- Ilijf - traagheidsmoment van de lijfplaat
- Itotaal - totaal traagheidsmoment
- Merk op dat \( I_{flens}+I_{lijf} = I_{totaal} \)
De dwarskracht wordt verondersteld alleen door het lijf van de ligger te worden opgenomen.
We kunnen dus aanzienlijke afschuifspanningen parallel aan de las verwachten, \( \tau_\parallel\), en wat normaal- en afschuifspanningen, \(\sigma_\perp.\) en \(\tau_\perp.\) als gevolg van buiging.
De grootte van \(\tau_\parallel\) kan worden berekend door de som te maken van de oppervlakken van de hoeklassen bij de lijfplaat van de ligger en de lijfplaat van de console:
\[A_w = 2 \cdot 5 \cdot 421 + 2 \cdot 5 \cdot 118 = 5390\textrm{ mm}^2\]
Dan kunnen we de verwachte equivalente spanning berekenen:
\[\tau_\parallel = V_{Ed} / A_w = 270 \cdot 10^3 / 5390=50 \textrm{ MPa}\]
De berekende spanning is lastig te vergelijken met de lasresultaten in IDEA StatiCa. CBFEM geeft een veel gedetailleerder en niet-uniform spanningsbeeld, waarbij rekening wordt gehouden met verschillende stijfheden en herverdeling van spanningen over de laslengte. Hierdoor ontstaat een spanningsverdeling die niet eenvoudig te vergelijken is met een handberekening.
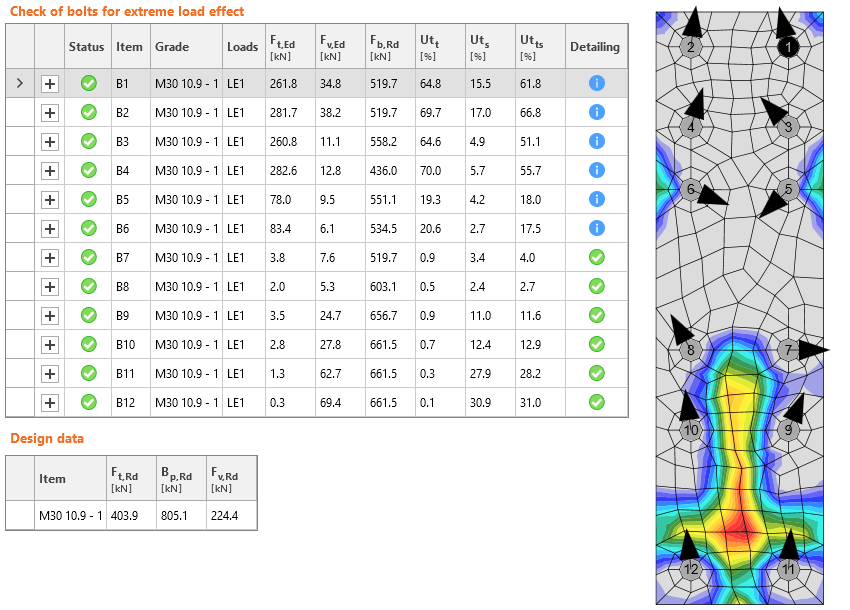
De belasting wordt via de kopplaat overgebracht naar de bouten. Gewoonlijk wordt aangenomen dat de afschuifkrachten gelijkmatig over alle bouten worden verdeeld. Als alternatief worden de bouten die het meest op trek worden belast buiten beschouwing gelaten en wordt aangenomen dat de bouten in de drukzone de afschuifkracht overbrengen.
\[ F_{v,Ed} = V_{Ed} / n = 270 / 12 = 22,5 \textrm{ kN} \].
waarbij:
- \(F_{v,Ed}\) - dwarskracht in één bout
- \(V_{Ed}\) - totale dwarskracht
- n - aantal bouten
De boutkrachten in IDEA StatiCa zijn vrij verschillend. Dit komt door de vervorming van de kopplaat en richting van de krachten.
De eerste rijen bouten worden op trek belast en de kopplaat maakt contact met de kolomflens ter hoogte van de onderflens van de console.
Om het buigend moment met de hand te berekenen, mogen de trekkrachten in de bouten plastisch worden aangenomen op voorwaarde dat aan punt 6.2.7.2 (9) wordt voldaan. In principe moet modus 1 of 2 (relatief dunne kopplaat of kolomflens vergeleken met bouten) van toepassing zijn om ductiel gedrag te garanderen.
Kolom
De belasting wordt overgedragen op de kolom via trek- en afschuifkrachten in de bouten en via contactspanningen tussen de kopplaat en de kolomflens.
Verschillende bewerkingen moeten worden uitgeschakeld:
De analyse stopt bij het bereiken van de lasweerstand bij 97% van de toegepaste belasting.
Dit is een verrassend resultaat. Het falen van de kolom op afschuiving zou een logische veronderstelling zijn. Op het tweede gezicht is het resultaat logisch: De kolom in afschuiving vervormt veel meer en hoewel dit niet tot bezwijken leidt (meer dan 5% plastische rekgrens), verhoogt het de belasting op andere onderdelen. De las is het meest bros en bezwijkt als eerste wanneer de omringende platen vervormen.