Webinar
Lateral Torsional Buckling of Precast Beams
-
2025-06-18T09:00:00.0000000Z(in Ihrer Ortszeit, 24-Stunden-Format)
Webinar Datum:
Nehmen Sie am Webinar teil und erfahren Sie mehr über
- What lateral-torsional buckling is and why long, prestressed beams are especially vulnerable
- How to assess every critical stage – lifting, transport, and final service – all in one analysis model
- How to define all inputs with confidence – imperfections, sling geometry, flexible supports
- How to run the GMNIA analysis and see second-order effects, internal forces, and deflections
- How to push results straight for code checks and generate ready-to-share reports
Sprecher
Orsolya Kartali
Product Engineer
IDEA StatiCa
IDEA StatiCa
Adam Kozousek
Produkt-Ingenieur
IDEA StatiCa
IDEA StatiCa
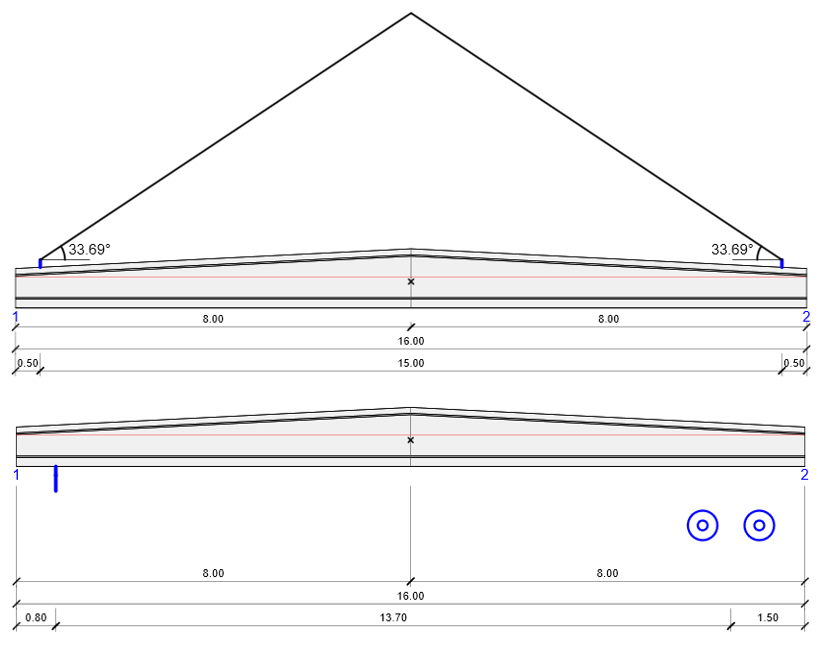
Slender precast beams can fail unexpectedly - not from lack of strength, but due to stability loss during lifting, transport, or service. With advanced GMNIA in IDEA StatiCa Beam, you can go beyond rough hand checks and ensure stability with confidence.
Several site incidents show that lateral-torsional buckling (LTB) is still one of the most costly and misunderstood stability problems in concrete construction. With the new advanced geometrically and materially non-linear LTB analysis in IDEA StatiCa Beam, you no longer have to rely on estimates when it comes to stability of prestressed or reinforced concrete beams.
Join our live webinar to learn, step by step, how to model, analyze, and code-check LTB so you can deliver safer, leaner designs quickly and avoid the financial and reputational hits that come from unexpected instability failures on site.
Who should attend?
- Structural engineers
- Bridge and precast designers
- Anyone responsible for the safety and economy of long concrete members
Resources
- Lateral stability for concrete beams – all inputs and outputs, analysis, and known limitations
- Lateral stability of long prestressed concrete beams during lifting
Register for free and join the live webinar on Wednesday, June 18, 2025, at 11:00 CEST (Prague time, UTC+2).
2025-06-18T09:00:00.0000000Z
1 Stunde