Description
A uniplanar T-joint of a rectangular hollow section brace to an open section chord, which is located in a lattice truss is studied. The RHS brace is welded directly onto the H or I chord, open sections, without use of reinforcing plates. The prediction by component-based finite element method (CBFEM) is verified with the failure modes method (FM) implemented in EN 1993-1-8:2005.
Analytical model
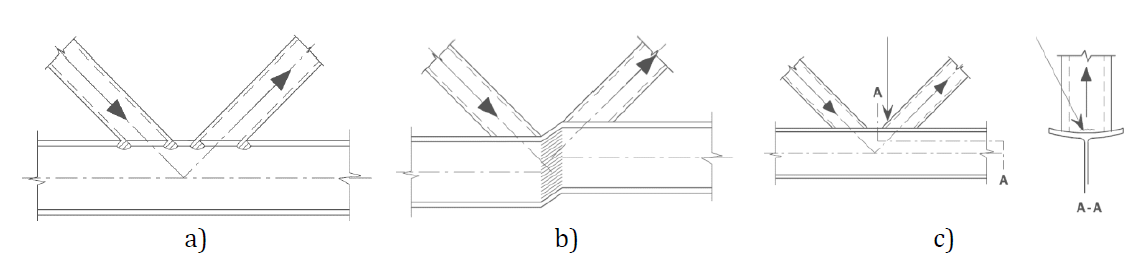
Three failure modes occur in the uniplanar T-joint of the welded rectangular hollow sections to the open sections: the local yielding of brace, called brace failure, the chord web failure, and the chord shear. All these failure modes are examined in this study; see Fig. 7.4.1. Welds are designed not to be the weakest component in a joint according to EN 1993-1-8:2005. The elements of lattice trusses are loaded by normal forces and bending moments. A point of action of internal forces of T-joint is described as follows:
Axially loaded H/I chord
Normal forces in the chord right and left of a T-joint act in the direction of chord longitudinal axis.
Diffraction loaded H/I chord
Bending moments right and left of a T-joint in plane of the T-joint are considered in the chord, and these bending moments rotate around one of the axes in plane of the chord cross-section for rotation in plane of the T-joint.
Axially loaded RHS brace
The normal force in the brace of a T-joint acts in the direction of brace longitudinal axis.
\[ \textsf{\textit{\footnotesize{Fig. 7.4.1 Major failure modes a) chord web failure, b) chord shear (in case of gap), c) brace failure}}}\]
The resistance of the chord web is determined using the method given in section 7.6 of the EN 1993-1-8:2005, which is described in (Wardenier et al,. 2010). The stresses from the brace are transferred through the flange of the chord to an effective area of the chord web. This area is located in the chord web at the point where the brace walls cross the chord web. The design axial resistance of the joint is the minimum of the design resistances:
Chord web failure
\[N_{\mathrm{i,Rd}} = \frac{f_{\mathrm{y0}} \cdot t_{\mathrm{w}} \cdot b_{\mathrm{w}}}{\sin(\theta_{\mathrm{i}}) \cdot \gamma_{\mathrm{M5}}}\]
Chord shear
\[N_{i,\mathrm{Rd}}=\frac{f_\mathrm{y0}\,A_\mathrm{v}}{\sqrt{3}\,\sin\theta_\mathrm{i}\cdot \gamma_{\mathrm{M5}}}\]
Brace failure
\[N_{i,\mathrm{Rd}}=2\,f_\mathrm{y1}\,t_\mathrm{1}\,p_{\mathrm{eff}}/\gamma_{\mathrm{M5}}\]
where
\[p_{\mathrm{eff}}=t_\mathrm{w}+2r+7\,t_\mathrm{f}\,\frac{f_\mathrm{y0}}{f_\mathrm{y1}}\]
and \(A_\mathrm{v}\) is the effective shear area.
The design bending resistance of the joint is the minimum of the design resistances:
Chord web failure
\[M_{\mathrm{ip,Rd}} = \frac{0.5 \, f_{\mathrm{y0}} \, t_{\mathrm{w}} \, b_{\mathrm{w}} \, h_1}{\gamma_{\mathrm{M5}}}\]
Brace failure
\[M_{\mathrm{ip,Rd}}=f_\mathrm{y1}\,t_\mathrm{1}\,b_{\mathrm{eff}}\,(h_\mathrm{1}-t_\mathrm{1})/\gamma_{\mathrm{M5}}\]
where
\[b_{\mathrm{w}} = \frac{h_1}{\sin \theta_{\mathrm{i}}} + 5 \cdot t_{\mathrm{f,0}} + r \;\leq\; 2 \, t_{\mathrm{i}} + 10 \cdot (t_{\mathrm{f,0}} + r)\]
\[b_{\mathrm{eff}}=t_\mathrm{w}+2r+7\,t_\mathrm{f}\,\frac{f_\mathrm{y0}}{f_\mathrm{y1}}\]
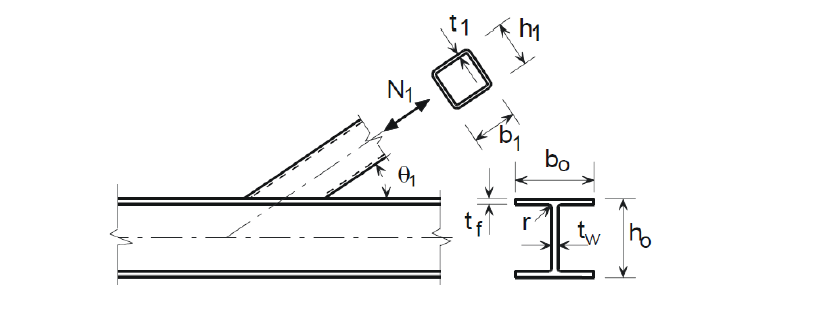
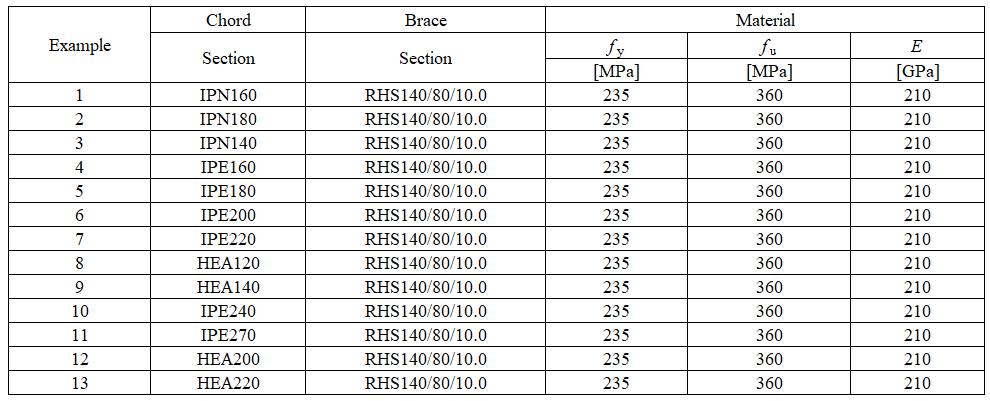
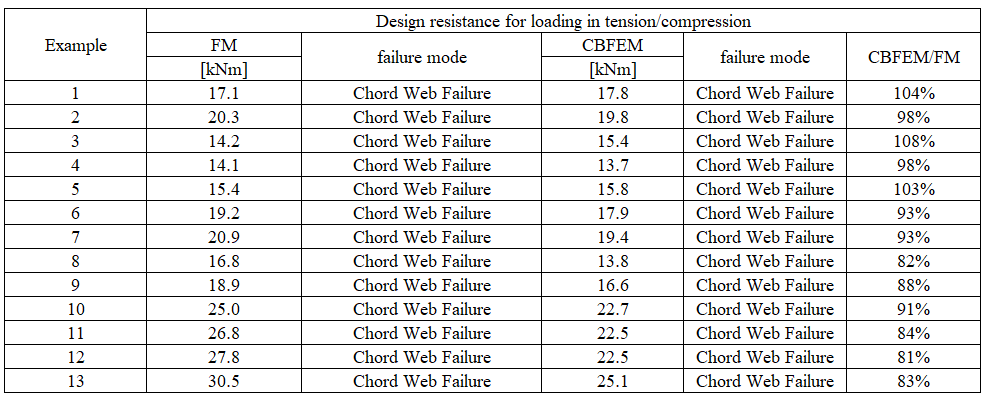
An overview of the considered examples loaded by axial force is described in Tab. 7.4.1. An overview of the considered examples loaded by bending moment is described in Tab. 7.4.2. A geometry of a joint with dimensions is shown in Fig. 7.4.2.
\[ \textsf{\textit{\footnotesize{Fig. 7.4.2 Joint geometry with dimensions}}}\]
Tab. 7.4.1 Examples of joints loaded by axial force
Tab. 7.4.2 Examples of joints loaded by in-plane moment
Verification of resistance
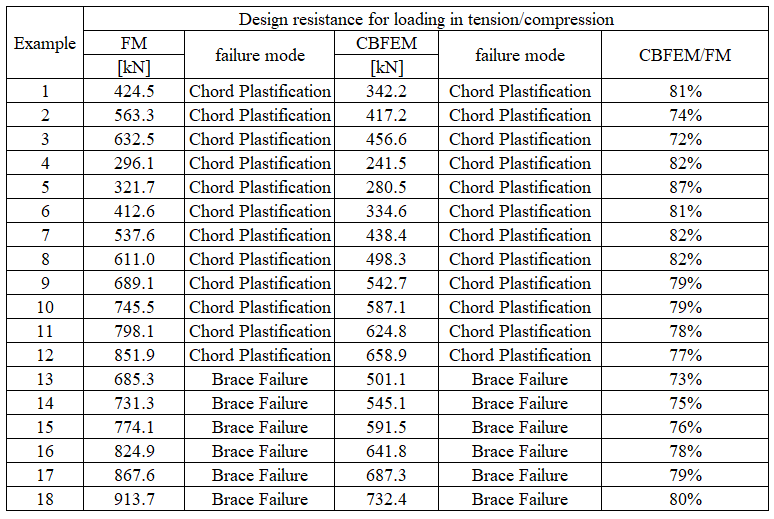
The study was focused on comparison of the failure models and the prediction of the design resistance. The results are presented in Tab. 7.4.3 and 7.4.4.
Tab. 7.4.3 Comparison of CBFEM and FM for axial force in brace
Tab. 7.4.4 Comparison of CBFEM and FM for in-plane moment in brace
The sensitivity study shows good agreement for all applied load cases. In the CBFEM method, the rounding of the wall of open cross-section is simplified, which brings a conservative estimate of the stress in the connected diagonal and the assumption of bearing capacity till 15 %. To illustrate the accuracy of the CBFEM model, the results of the parametric studies are summarized in a diagram comparing design resistances by CBFEM and FM; see Fig. 7.4.3.
\[ \textsf{\textit{\footnotesize{ Fig. 7.4.3 Verification of CBFEM to FM for axial force and bending moment in the brace}}}\]
Range of validity
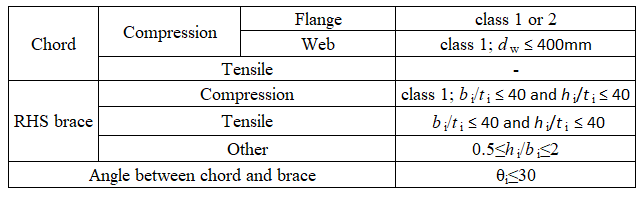
Range of validity, on which is verified CBFEM for T-joints between rectangular hollow section and open section, is defined in Table 7.20 of EN 1993-1-8:2005, see Tab. 7.4.5. In case of application of the CBFEM model outside the range of validity of FM, the validation to experiments or verification to validated research model should be prepared to approve the quality of prediction.
Tab. 7.4.5 Range of validity of T-joints
Benchmark example
Inputs
Chord
• Steel S235
• IPN280
Brace
• Steel S235
• RHS 140×80×10
Mesh size
• 16 elements on the biggest web of rectangular hollow member
Outputs
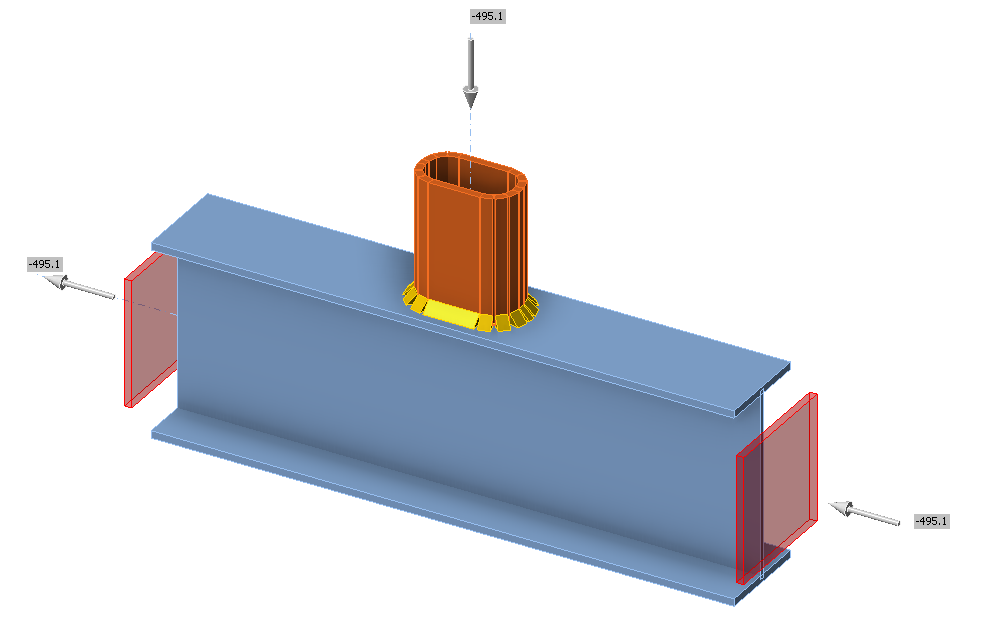
• Design resistance in compression/tension Fc,Rd = 457 kN (It should be noted that the resistance was calculated using the "Stop at limit strain" function. Consequently, the actual CBFEM resistance may be marginally higher.)
• Collapse mode is chord plastification
\[ \textsf{\textit{\footnotesize{Fig. 7.4.4 Benchmark example for chord IPE270 and brace RHS 140×80×10}}}\]