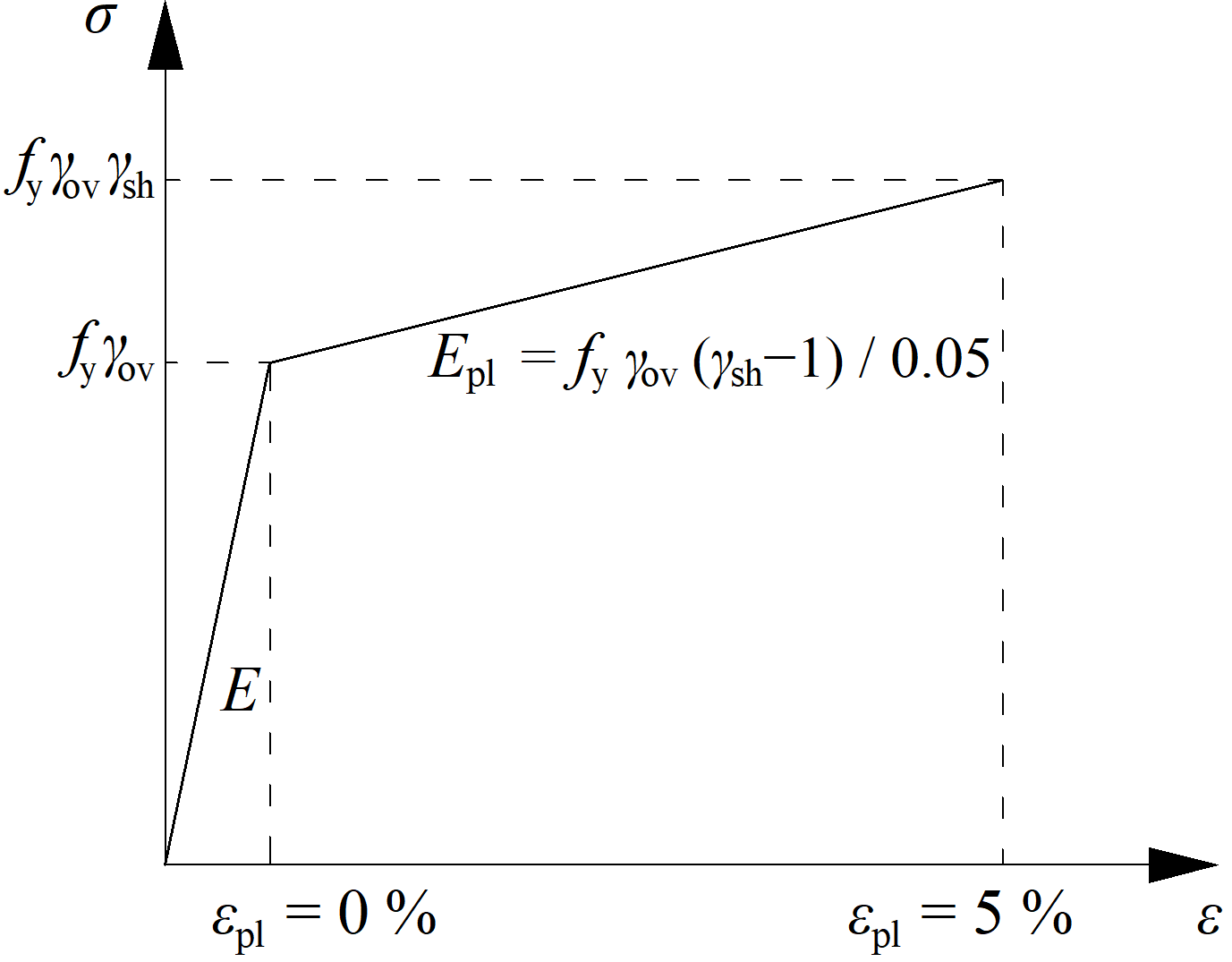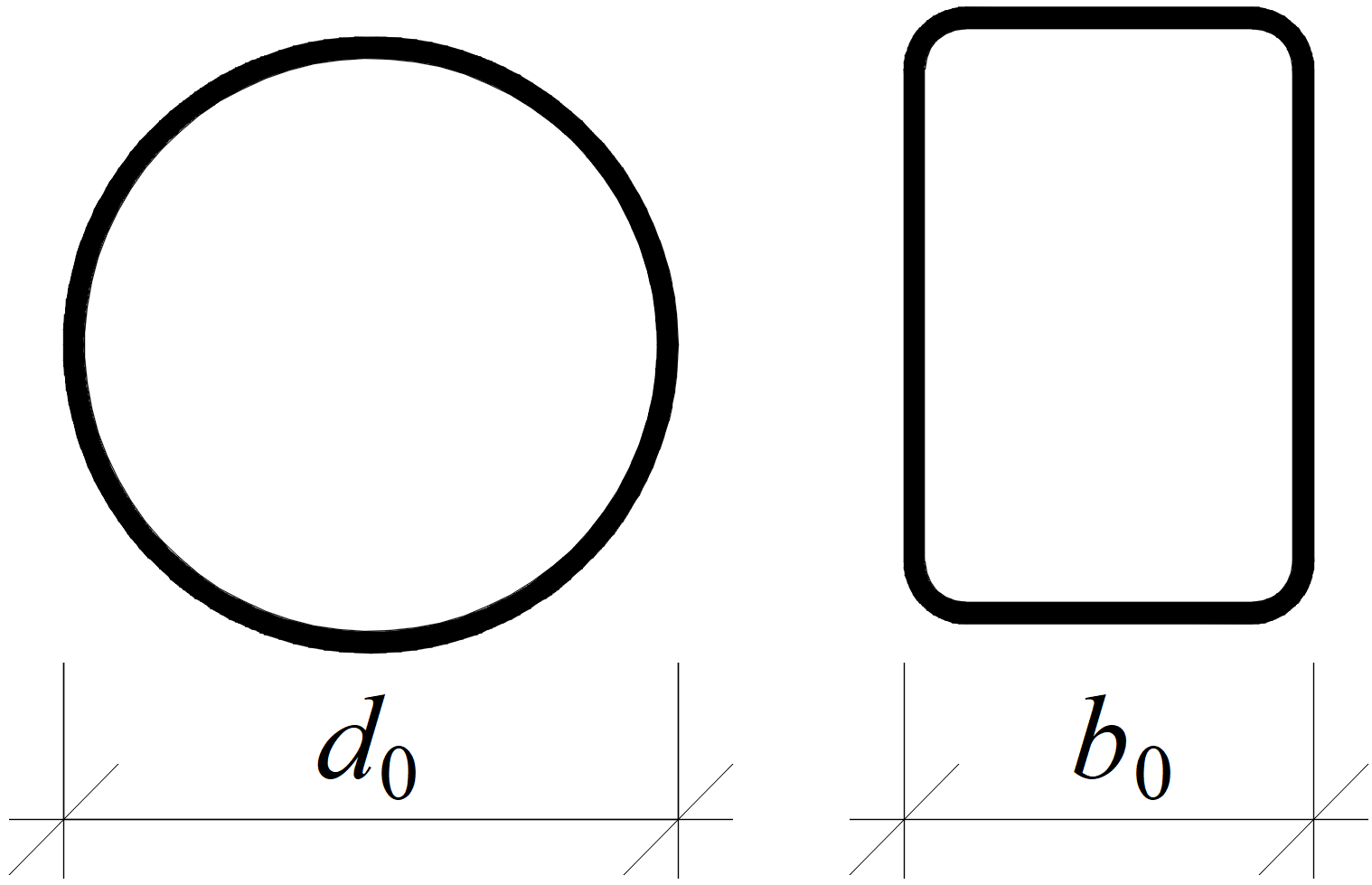Общие теоретические основы

Общая информация

Введение

При расчёте стальных конструкций они зачастую моделируются стержневыми элементами. Однако, многие области конструкции не соответствуют стержневым моделям, например, сварные или болтовые соединения, опорные узлы и отверстия вс тенах, места изменений сечения и приложения сосредоточенных нагрузок. Расчёт таких областей весьма сложен и требует особого внимания. Также стоит учитывать нелинейное поведение конструкции, которая может проявляться, например, в материале пластин, контактных поверхностях между фланцами или опорной плитой и бетонным блоком, односторонние эффекты при моделировании анкеров и сварных швов и т.д. В нормах проектирования, н-р, EN 1993-1-8 и технической литературе предлагается множество инженерных решений подобных вопросов. Их общая идея – упрощение и типизация моделей и нагрузок. Чаще всего используется компонентный метод.

Компонентный метод

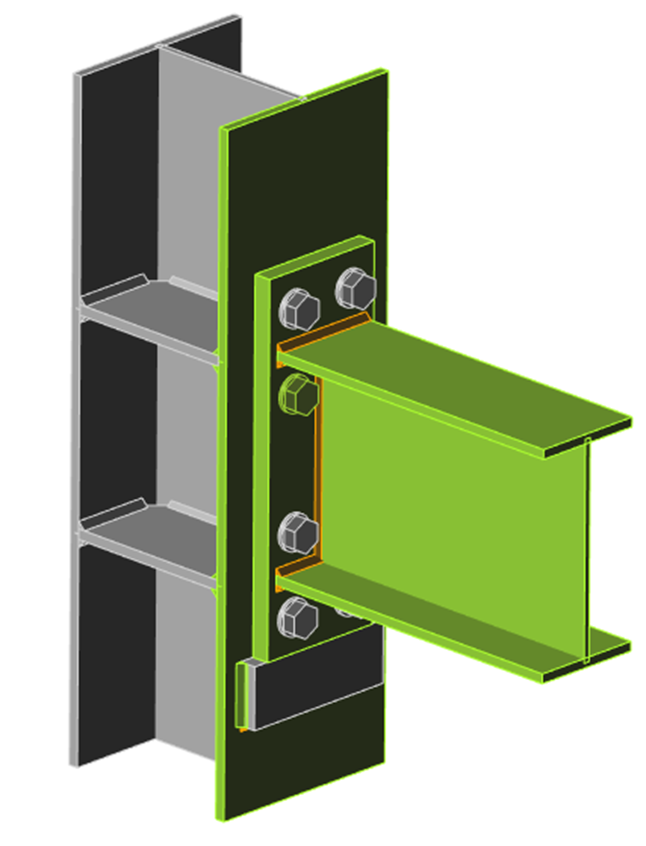
Компонентный метод (КМ) рассматривает узел как совокупность связанных элементов – компонентов. Соответствующая расчётная модель строится для каждого типа узла и позволяет вычислить усилия и напряжения в каждом компоненте – см. картинку ниже.

Компоненты узла с фланцами на болтах моделируются упругими связями

Каждый компонент проверяется отдельно по своим формулам. В силу того, что для каждого типа узла приходится строить отдельную модель, компонентный метод весьма ограничен и плохо подходит для сложных узлов, нагруженных произвольным образом.

Совместно с коллективом Кафедры Стальных и Деревянных Конструкций Факультета Гражданского Строительства в Праге и Институтом Металлических и Деревянных Конструкций Факультета Гражданского Строительства Технологического Университета в Брно компания IDEA StatiCa разработала новую продвинутую методику для расчёта узлов стальных конструкций.

Особенности нового Компонентного метода конечных элементов (КМКЭ) состоят в следующем:

• Универсальность. Метод применим к большинству типов соединений, опорных узлов, деталей, встречающихся в инженерной практике.
• Удобство и быстрота. КМКЭ очень прост для использования в ежедневной практике, результаты расчёта можно получить гораздо быстрее по сравнению с другими программами.
• Комплексное решение. КМКЭ даёт инженеру понятную информацию о работе узла, его напряжённо-деформированном состоянии и резервах несущей способности отдельных компонентов, а также общие данные о безопасности и надёжности конструкции

В основу КМКЭ заложен следующий принцип: многие верифицированные модели КМ и его сильные стороны сохраняются. Слабое место КМ – его универсальность при вычислении напряжений в отдельных компонентах, заменяется методом конечных элементов (МКЭ) и соответствующими расчётами. 

МКЭ весьма универсален и очень часто используется для расчёта строительных конструкций. Его применимость к моделированию узлов любой формы кажется вполне обоснованной (Virdi, 1999). Подразумевается, что расчёт должен быть упругопластическим, так как сталь в строительных конструкциях обычно подвержена текучести. Фактически, результаты упругого расчёта для узлов являются бесполезными.

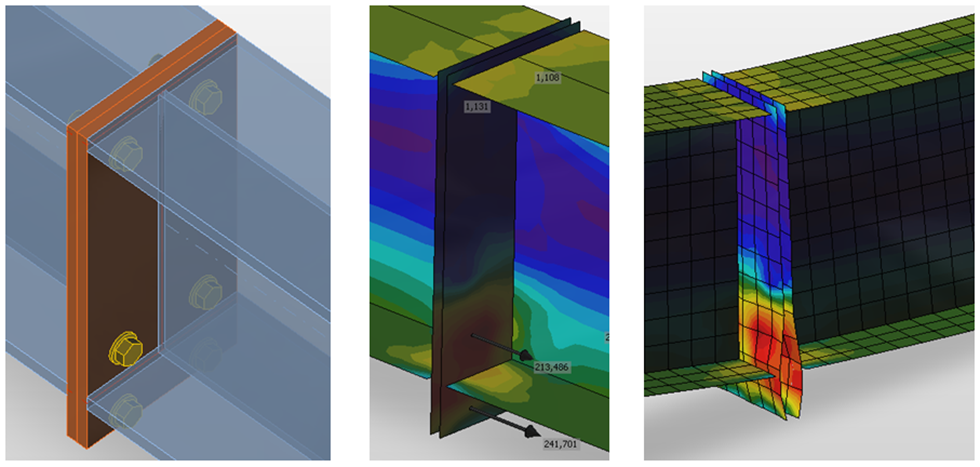
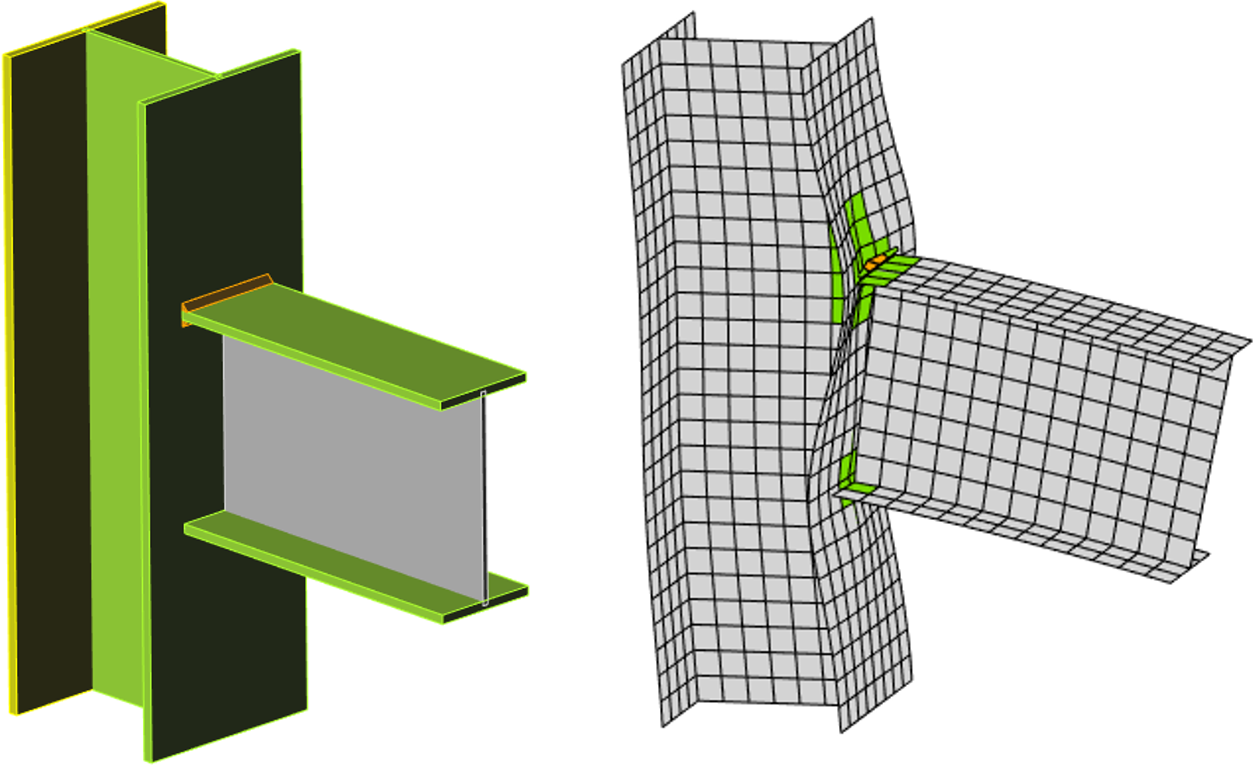
МКЭ модели используются для исследования поведения узла, который моделируется объёмными элементами с заданными характеристиками реального материала.

КМКЭ модель фланцевого соединения на болтах

И стенки, и полки соединяемых элементов в КМКЭ моделируются плоскими конечными элементами, для которых давно доступно известное решение.

Крепёжные элементы – болты и сварные швы – одно из самых проблемных мест при построени расчётной модели. Их моделирование в МКЭ программах общего вида – очень сложная задача, так как они не предоставляют всех необходимых свойств для описания этих моделей. Поэтому для сварки и болтов были разработаны специальные КЭ модели.

КМКЭ модель фланцевого соединения на болтах

При расчёте стальных каркасов или балочных клеток узлы моделируются точками, не имеющими массы. Для узлов записываются уравнения равновесия, и затем в ходе расчёта всей конструкции находятся внутренние усилия по концам каждого стержневого элемента. Фактически, узел испытывает воздействие именно этих усилий, равнодействующая которых равна нулю – так как узел при статическом нагружении находится в равновесии. 

В расчётной схеме конструкции (н-р, каркаса) реальная форма узла не учитывается. Расчётчик лишь задаёт тип поведения этого узла – шарнирный или жёсткий.

Для корректного расчёта и конструирования узла должна создаваться надёжная модель, учитывающая его реальное состояние и размеры. В КМКЭ размеры узла зависят от размеров сечений – расстояние от узла до конца элемента составляет примерно 2-3 высоты его сечения. Эти участки моделируются пластинчатыми элементами.

Теоретический (безмассовый) узел и реальный - с учётом размеров элементов, но без креплений

Для большей точности КМКЭ модели усилия с торцов 1D элементов прикладываются как нагрузки к концам элементов в IDEA StatiCa. Все 6 составляющих внутренних усилий прикладываются к концу элемента – их значения сохраняются, за исключением моментов, которые пересчитываются в соответствии с заданными плечами сил.

Концы отдельных элементов никак не соединяются друг с другом. Поэтому для моделирования всех соединений и стыков элементов друг с другом используются так называемые монтажные операции. Они подразделяются на: вырезы, смещения, отверстия, рёбра жёсткости, торцевые пластины и стыки, уголки, фасонки и другие. К ним, как правило, добавляются элементы крепежа – сварные швы и болты. Таким образом элементы крепятся друг к другу.

В IDEA StatiCa Connection можно выполнить два типа расчёта:

1. Геометрически линейный, но физически нелинейный расчёт с учётом контактных поверхностей для получения напряжённо-деформированного состояния (НДС) узла,
2. Расчёт с вычислением собственных чисел для определения коэффициентов запаса устойчивости узла.

При расчёте узлов учёт геометрической нелинейности не нужен ввиду того, что его расчётная модель строится из тонких пластин. Их гибкость может быть определена при помощи расчёта узла на устойчивость (вычисления собственных чисел). В разделе 3.9 приводится описание границ применимости геометрически линейного расчёта с точки зрения предельной гибкости. Геометрическая нелинейность в программе не учитывается за исключением случаев использования отдельной опции в Настройках норм.

CBFEM Components

Модель материала

Для описания работы материала стальных конструкций, как правило, используются следующие модели (диаграммы работы): упруго-идеально-пластическая, идеально-упругая упрочняющаяся и истинная диаграмма напряжение-деформация. Истинная диаграмма работы строится по результатам испытаний лёгких сталей на растяжение при заданной температуре окружающей среды. Истинные значения напряжения и деформации могут быть получены из следующих формул:

\[ \sigma_{ист}=\sigma (1 + \epsilon) \]

\[ \epsilon_{ист}=\ln (1 + \epsilon) \]

где σ_ист – истинное напряжение, ε_ист – истинная деформация, σ и ε – номинальное напряжение и деформация.

Пластины в IDEA StatiCa Connection моделируются упругопластическими с условным пределом текучести, выраженным практически горизонтальной ветвью на диаграмме работы согласно EN1993-1-5, п. С.6, (2) с небольшим наклоном, равным tan^-1 (E/1000). Поведение материала подчиняется критерию текучести по фон Мизесу. Считается, что вплоть до достижения условного предела текучести fyd материал работает упруго, f_yd.

Критерием наступления предельного состояния для областей, не подверженных потере устойчивости, является достижение главной мембранной деформацией предельной величины. Рекомендуется использовать значение предельной пластической деформации, равное 5% (см. EN1993-1-5 app. C par. C8 note 1).

Диаграммы работы материала в численных моделях

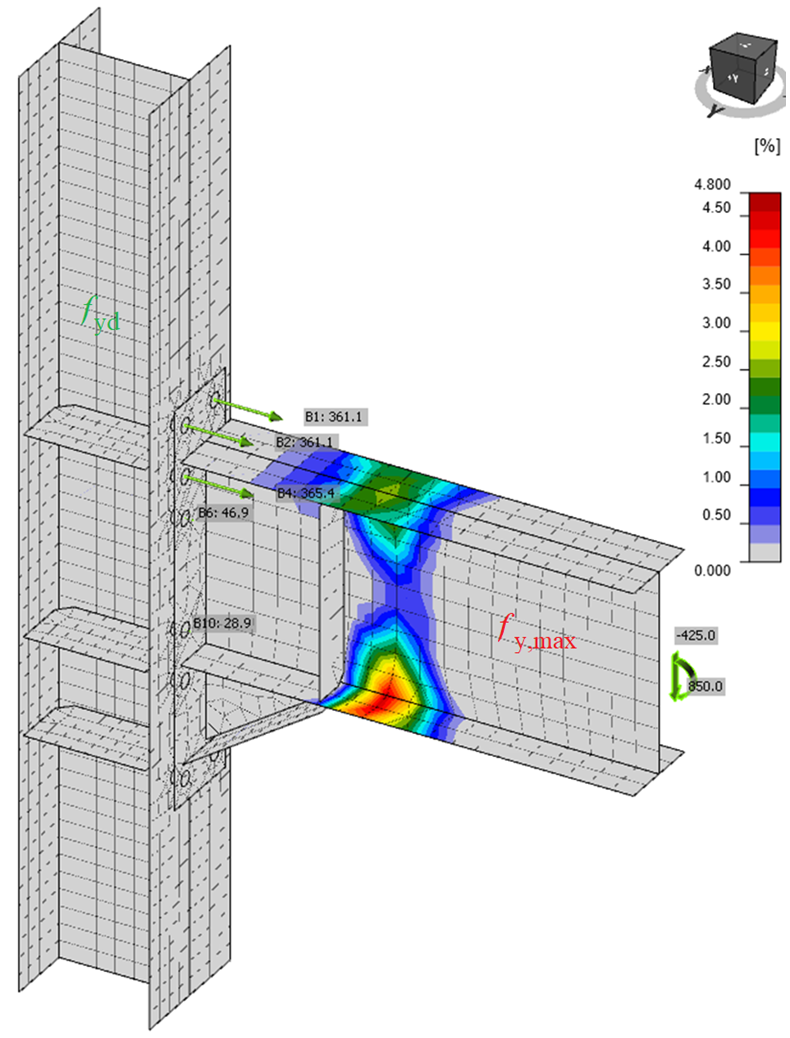
Величина предельной пластической деформации часто служит предметом для дискуссий. По правде говоря, в упруго-идеально-пластической модели предельная нагрузка не сильно чувствительна к величине предельной пластической деформации. Продемонстрируем это на примере стыка балки с колонной. Балка двутаврового профиля IPE 180 крепится к двутавровой колонне HEB 300 и загружается изгибающим моментом.

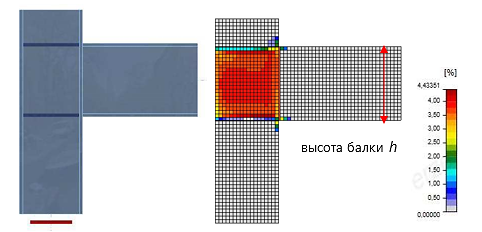
Влияние величины предельной пластической деформации на расчётную несущую способность балки показано ниже. Предельная пластическая деформация менялась от 2% до 8%, но при этом изменение несущей способности (предельного момента) составило менее 4%

Нагрузки, эквивалентные напряжения и деформации в узле. Пример возможного наступления предельного состояния стыка балки с колонной

Влияние величины предельной пластической деформации на предельный момент

Модель пластин, сетка конечных элементов и сходимость расчёта

Увеличение количества конечных элементов обеспечит большую точность результов, но потребует больших затрат машинного времени.

Модель пластин

Для моделирования пластин в соединениях стальных конструкций рекомендуется использовать КЭ оболочек. Здесь применяются четырёхузловые (четырёхугольные) элементы оболочек, узлы пластины находятся в её углах. В каждом узле имеется по 6 степеней свободы: 3 поступательные (u_x, u_y, u_z) и 3 вращательные (φ_x, φ_y, φ_z). Деформации элемента разделяются на мембранные и изгибные составляющие.

За основу поведения КЭ оболочки в плоскости взята работа Ибрагимбеговича (Ibrahimbegovic, 1990). Учитываются углы поворота, перпендикулярные плоскости элемента. Обеспечивается полное трёхмерное описание элемента. Сдвиговые деформации из плоскости учитываются формулировками, описывающими поведение изгибаемых пластин, согласно гипотезе Миндлина (Mindlin). Используются элементы типа MITC4, см работу Дворкина (Dvorkin, 1984). Пластина имеет 5 точек интегрирования по высоте, появление пластических деформаций фиксируется в каждом слое (каждой точке). Подобный способ носит название «интегрирование по Гауссу-Лобатто (Gauss - Lobatto integration). Нелинейная стадия работы выявляется для каждого слоя на основе известных относительных деформаций.

Сходимость решения и сетка конечных элементов

При генерации сетки конечных элементов расчётной модели необходимо следовать определённым правилам. Результаты проверки соединения не должны зависеть от размера сетки КЭ. Разбивка отдельных пластин на конечные элементы обычно не вызывает сложности. Особое же внимание следует уделять сложным геометрическим объектам, таким как укреплённые панели, Т-образные стыки и опорные пластины. Для таких моделей необходимо выполнять сопоставление получаемых результатов в зависимости от размера сетки КЭ.

Все КЭ пластин балочных элементов, которыми моделируются сечения, имеют одинаковый размер. Размер КЭ ограничен заданными значениями. По умолчанию минимальный размер элемента составляет 10 мм, а максимальный – 50 мм. Сетки стенок и поясов элементов не зависят друг от друга. Число КЭ по высоте сечения по умолчанию равно 8, как показано на рисунке ниже. Пользователь может изменить значения, используемые по умолчанию, в Настройках норм.

Сетка балочного элемента с объединением перемещений между стенкой и поясами

Генерация сетки КЭ торцевых пластин производится независимо от других частей соединения. По высоте пластина разбивается по умолчанию на 16 элементов, как показано на рисунке ниже.

Сетка КЭ торцевой пластины, 7 элементов по ширине

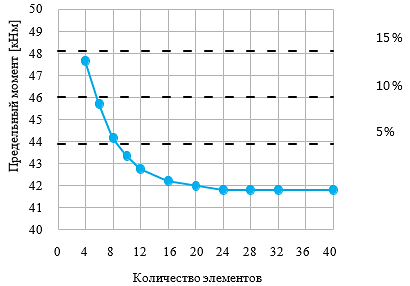
Следующий пример - стык балки с колонной показывает, как влияет размер сетки КЭ на предельный момент. Балка двутаврового профиля IPE 220 крепится к двутавровой колонне HEA200 и загружается изгибающим моментом, как показано на следующем рисунке. Критическим компонентом здесь является стенка колонны, подверженная срезу. Число КЭ по высоте сечения меняется от 4 до 40, для каждого случая оцениваются результаты и затем производится их сравнение. Пунктирные линии показывают различия в результатах, равные 5%, 10% и 15%. Рекомендуется производить разбивку сечения по высоте на 8 конечных элементов.

Стык балки с колонной и пластические деформации в предельном состоянии

Влияние количества элементов вдоль края на предельный момент

Ниже приводится пример исследования чувствительности к размеру сетки тонкой пластины - сжатого ребра жёсткости, установленного на колонне. Геометрия модели берётся по примеру из раздела 6.3. Количество элементов по ширине ребра жёсткости меняется от 4 до 20 и производится сравнение результатов. Первая форма потери устойчивости и влияние количества элементов на устойчивость узла и величину предельного момента приводятся на рисунках ниже. На графиках показаны различия в 5% и 10%. Для расчётов рёбер жёсткости (пластин) рекомендуется принимать 8 элементов по ширине.

Первая форма потери устойчивости и влияние числа элементов вдоль ребра жёсткости на предельный момент

Также рассматривается пример влияния крупности сетки на результаты на примере Т-образного фланцевого соединения. Геометрия фланцевого соединения описана в разделе 5.1. Половина ширины фланца разбивается на элементы – от 8 до 40, и минимальный размер элемента принимается равным 1 мм. Влияние числа элементов на расчётное сопротивление фланцевого узла поясняется на рисунках. Пунктирные линии обозначают расхождения в 5%, 10% и 15% соответственно. Для расчётов рекомендуется принимать 16 элементов по ширине половины фланца.

Влияние числа элементов на пред. нагрузку на фланцевое соединение

Контактные поверхности

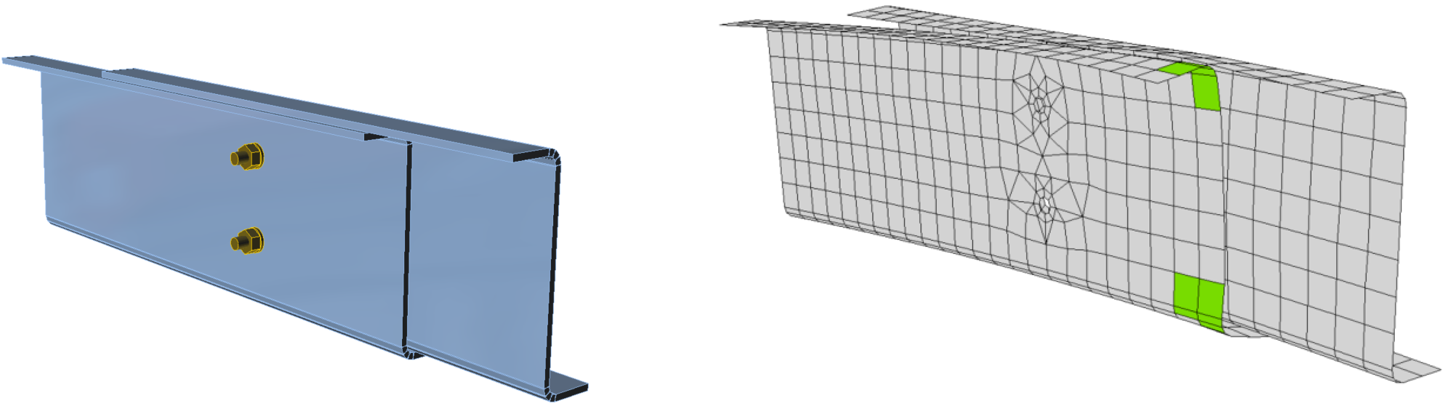
Для моделирования контактных поверхностей обычно используется стандартный метод «пенальти». Если в схеме имеется узел, проникающий в поверхность соседней пластины, то между этим узлом и пластиной добавляется «штрафная» жёсткость. В процессе итерационного расчёта эта жёсткость контролируется специальным алгоритмом («эвристическим») для достижения лучшей сходимости. Решатель автоматически определяет узлы расчётной схемы, проникающие в соседние пластины, и вычисляет распределение контактных напряжений между этими узлами и пластинами. Это позволяет создавать контактные зоны с разной сеткой на пластинах, как показано на рисунке. Преимуществом метода «пенальти» является автоматизация создания расчётной модели. Контактные зоны между пластинами существенно влияют на распределение напряжений между элементами узла.

Пример, демонстрирующий работу контактных зон между стенками и полками Z-образных профилей

Программа позволяет создавать контактные поверхности между

• двумя поверхностями (гранями),
• двумя краями (торцами),
• краем (торцом) и поверхностью (гранью).

Пример контакта между двумя краями – торцом фланца и опорного столика

Пример контакта между краем и поверхностью – торцом нижней полки балки и гранью колонны

Напряжения в контактных поверхностях могут быть отображены на 3D виде, а их значения выводятся в таблицу проверки пластин. Однако, эти значения не используются в проверках и носят исключительно информативный характер. Напряжения в пластинах из плоскости и за счёт давления слоёв друг на друга также не учитываются. 

Сварные швы

Существует несколько вариантов численного моделирования сварных швов. Отказ от предположения малости перемещений и переход к большим деформациям значительно усложняют расчёты. Однако имеется возможность различного описания сетки КЭ, использования других кинематических вариаций и соответствующих моделей. Используемые в повседневной практике различные геометрические модели - 2D и 3D, имеют различную степень приближения к реальным результатам. Чаще всего используется пластическая модель материала, не зависящая от скорости нагружения, с критерием текучести по Фон-Мизесу. Ниже описывается два подхода для описания сварных швов. Остаточные напряжения, вызванные сваркой, расчётной моделью не учитываются.

Сварка - Непосредственное соединение пластин

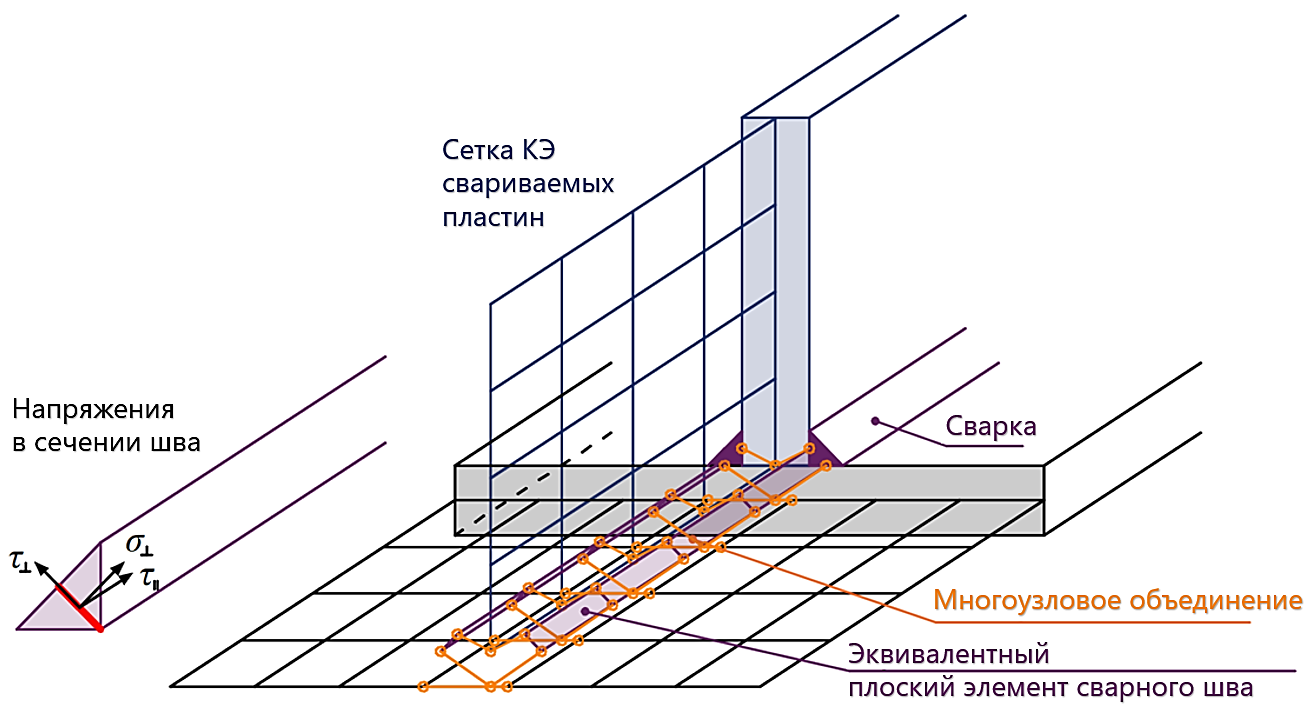
Первый подход состоит в моделировании сварного шва между пластинами путём прямого объединения узлов сетки пластин в окрестностях шва. Нагрузка передаётся с одной пластины на другую через специальные ограничения, в основу которых заложена формулировка Лагранжа для усилий и деформаций. Это называется многоузловым объединением (multi point constraint - MPC), связывающим узлы сетки одной пластины с узлами другой. Но при этом узлы сеток не соединяются напрямую друг с другом. Преимуществом такого подхода является возможность стыковки несогласующихся сеток КЭ (разной крупности). Таким образом, данный способ позволяет замоделировать срединную поверхность присоединяемой пластины с небольшим смещением, с некоторым приближением к реальному положению сварного шва и его толщине. Передача нагрузки на сварной шов происходит через МРС, таким образом находятся напряжения в сечении сварного шва. Этому стоит уделять особое внимание при вычислении напряжений в пластине под сварным швом и при моделировании тавровых соединений.

Сварка – Упругопластические элементы с перераспределением пластических деформаций

Модель с многоузловым объединением не учитывает жёсткость сварного шва, а напряжения вычисляются с большим запасом. Пики напряжений, возникающие на концах сварных швов, в углах и закруглениях, влияют на прочность всего сварного шва, хотя отдельные его участки могут быть менее нагруженными. Для устранения этого эффекта была разработана улучшенная модель сварных швов. Суть её в том, что между пластинами добавляются специальные упругопластические элементы, учитывающие положение сварного шва, его ориентацию и толщину. Добавляемый эквивалентный объёмный КЭ сварного шва имеет размеры, соответствующие размеру сварного шва. Материал данного объёмного элемента работает нелинейно, поведение шва считается упругопластическим. Момент появления пластического течения при упруго-идеально-пластической работе отслеживается по величинам напряжений в сечении сварного шва. Пики напряжений перераспределяются вдоль большей части сварного шва.

Оценка напряжений в сварном шве

Пластическая модель сварных швов даёт истинные значения напряжений, и необходимости в дальнейшей интерполяции результатов нет. Вычисленные значения напрямую используются для проверок. В этом случае больше нет необходимости занижать прочность сварных швов с ломаной осью, швов у неподкреплённых полок и длинных швов.

Ограничения между конечными элементами сварки и узлами сетки 

Сварные швы общего вида, использующие пластическое распределение, могут быть непрерывными, частичными или прерывистыми. Непрерывные сварные швы устраиваются по всей заданной грани, частичный сварной шов задаётся так же, но со смещениями в начале и конце, а при задании прерывистых швов можно назначать длины привариваемых участков и зазоры между ними.

Обычные и преднапряжённые болты

Болты

В КМКЭ болты моделируются нелинейными упругими связями, воспринимающими растяжение, срез и смятие соответственно. При растяжении болт заменяется упругой связью, имеющей только продольную жёсткость, предел прочности, а также начальный предел текучести и деформативности. Продольная жёсткость описывается аналитически, как в VDI2230. Модель хорошо отвечает экспериментальным данным (см. Gödrih, 2014). При задании предела текучести и деформативности считается, что пластическая деформация возникает только в резьбовой части тела болта.

Зависимость деформаций от усилия при смятии пластины

Данная зависимость строится по следующим уравнениям и формулам:

Упругая жёсткость:

\( k=\frac{E A_s}{L_b} \)

Пластическая жёсткость:

\[ k_t = c_1 k \]

Усилие на границе упругости:

\[ F_{t,el} = \frac{F_{t,Rd}}{c_1 c_2 - c_1 +1} \]

Деформация на границе упругости:

\[ u_{el} = \frac{ F_{t,el} }{k} \]

Деформация на границе пластичности:

\[ u_{t,Rd} = c_2 u_{el} \]

где:

• E – модуль упругости болта
• A_s – площадь сечения болта нетто (по резьбе)
• L_b – рабочая длина, то есть, размер пакета (сумма толщин пластин, стянутых болтом), толщина шайб, половина толщины гайки и половина толщины головки болта
• F_t,Rd – предел прочности болта при растяжении
• \( c_1 = \frac{R_m - R_e}{\frac{1}{4} A E - R_e} \)
• \( c_2 = \frac{AE}{4 R_e} \)

В окрестностях отверстия от болта на пластину передаются только сжимающие усилия. Это осуществляется при помощи специальных интерполяционных вставок между узлами тела болта и узлами краёв отверстий. Деформационная жёсткость элемента оболочки, которыми моделируются пластины, распределяет усилия между болтами и обеспечивает имитацию процесса смятия пластины.

Отверстия под болты по умолчанию назначаются круглыми, но могут быть овальными (их форму можно изменить в редакторе пластин). Болты в обычных (круглых) отверстиях могут воспринимать срезающие усилия по всем направлениям, в то время как болты в овальных отверстиях могут свободно перемещаться по горизонтали или вертикали, не воспринимая поперечных усилий по этим направлениям.

Совместное действие продольной и поперечных сил в болте может быть напрямую учтено его расчётной моделью. Такое распределение усилий достаточно приближено к реальности (см. диаграмму). Болты, подверженные высоким растягивающим усилиям, воспринимают меньшие срезающие усилия и наоборот.

Диаграмма взаимодействия растягивающего и срезающего усилий (Еврокод)

Преднапряжённые болты

Преднапряжённые болты используются в случаях, когда требуется минимизировать деформации узла. Поведение таких болтов при растяжении аналогично обычным болтам. Сдвигающее усилие в таких соединениях воспринимается не смятием пластин, а трением между ними (болто-контактом).

Расчётная прочность болто-контакта на срез для преднапряжённых болтов (класса прочности 8.8 и выше) зависит от величины приложенного растягивающего усилия.

В IDEA StatiCa Connection выполняется проверка фрикционных соединений именно на восприятие сдвигающего усилия болто-контактом (проверка деформаций соединения на малость – в таких соединениях не должно возникать проскальзывания). Если наблюдается проскальзывание, преднапряжённые болты не проходят проверку по деформациям. В таком случае после необходимо выполнить проверку болтов, считая их обычными, воспринимающими срез, растяжение и передающими смятие на соединяемые пластины.

Пользователь сам выбирает, какую проверку следует выполнять – на восприятие усилий за счёт трения (2 ГПС) либо же на прочность (смятие, срез и растяжение) после проскальзывания (1 ГПС). Выполнить обе проверки сразу для одного узла нельзя. Подразумевается, что после проскальзывания фрикционное соединение работает как соединение на обычных болтах, которые при этом могут проверяться на срез, растяжение и смятие пластин.

Изгибающий момент, приложенный к соединению, оказывает несущественное влияние на несущую способность болто-контакта. Тем не менее было принято выполнять проверку на трение для каждого болта отдельно. Эта проверка встроена в КМКЭ модель болта. В общем случае сложно сказать, является ли внешняя растягивающая нагрузка в болте нагрузкой от момента или растягивающей нагрузки, приложенной к узлу.

Изополя напряжений в соединении на обычных болтах и высокопрочных

Анкерные болты

Анкерные болты моделируются по тем же принципам, что и обычные. Только в этом случае болт с одного конца закрепляется в бетоне. Его длина, L_b,берётся как сумма толщин шайбы, t_w, опорной плиты, t_bp, слоя раствора, t_g, и свободной длины анкера в бетоне, которая предполагается равной 8d, где d – диаметр анкера (этот коэффициент может быть изменён в Настройках норм и расчётов). Это значение берётся в соответствии с положениями Компонентного Метода (EN 1993-1-8); значение свободной длины анкера в бетоне также может быть изменено в Настройках норм и расчётов. Осевая жёсткость анкеров при растяжении определяется как k = E A_s / L_b. 

Диаграмма работы анкерных болтов приводится на следующем рисунке. Ниже даются сводная таблица и общие формулы из ISO 898:2009.

Диаграмма работы анкерного болта

\[ F_{t,el}=\frac{F_{t,Rd}}{c_1 c_2 - c_1 + 1} \]

\[ k_t = c_1 k; \qquad c_1 = \frac{R_m - R_e}{\left ( \frac{1}{4} A - \frac{R_e}{E} \right )E} \]

\[ u_{el} = \frac{F_{t,el}}{k}; \qquad u_{t,Rd} = c_2 u_{el}; \qquad c_2 = \frac{AE}{4R_e} \]

где:

• A – удлинение анкера
• E – модуль Юнга (упругости)
• F_t,Rd – прочность стали анкера при растяжении
• R_m – предел прочности стали (при растяжении)
• R_e – предел текучести

Жёсткость анкерных болтов при сдвиге принимается как для обычных болтов.

Анкерные болты с зазором

Анкеры с зазором могут проверяться на стадии монтажа перед тем, как зазор заполняется на постоянной основе. Анкерные болты с зазором моделируются стержневыми элементами, нагруженными срезающим усилием, изгибающим моментом и/или сжимающим или растягивающим усилием. Эти величины определяются в процессе МКЭ расчёта. Анкер закрепляется с двух сторон, с одной стороны – на 0,5d ниже поверхности бетона, а с другой – в середине толщины опорной пластины. При расчёте на устойчивость для расчётной длины стержня обычно берётся коэффициент, равный двум. В расчётах используется пластический момент сопротивления. Форма эпюры изгибающих моментов зависит от соотношения жёсткостей анкеров и опорной плиты.

Анкеры с зазором – плечо поперечной силы и расчётные длины; первый случай (жёсткие анкеры) более консервативный

Бетонные блоки

Расчётная модель

В КМКЭ удобно моделировать бетонный блок контактными 2D элементами. Это значительно упрощает расчёты. Контактные элементы между бетоном и опорной плитой работают только на сжатие. Сжимающие напряжения находятся по модели Винклера-Пастернака и определяют деформации бетонного блока. Растягивающие усилия между опорной плитой и бетоном воспринимаются только анкерными болтами. Сдвигающее усилие воспринимается трением по границе стали и бетона, противосдвиговым упором и анкерами (за счёт изгибной жёсткости). Прочность анкеров при сдвиге оценивается аналитически. Трение и противосдвиговой упор моделируются как полное одноузловое ограничение в плоскости контакта стали и бетона.

Жёскость при деформировании

Бетонный блок при расчёте опорных узлов колонн может быть определён как упругое полупространство с заданной жёсткостью. Для упрощения расчётов фундаментов обычно используется модель упругого основания (далее – УО) Винклера-Пастернака. Его жёсткость определяется с учётом модуля упругости бетона и эффективной высоты УО по формуле:

\[ k = \frac{E_c}{(\alpha_1 + \upsilon) \sqrt{\frac{A_{eff}}{A_{ref}}}} \left( \frac{1}{\frac{h}{a_2 d} + a_3}+a_4 \right) \]

где:

• k – жёсткость бетонного основания при сжатии
• E_c – модуль упругости бетона
• υ – коэффициент Пуассона бетона фундамента
• A_eff – эффективная площадь при сжатии
• A_ref = 10 m² – опорное значение площади
• d – ширина опорной плиты
• h – высота бетонного блока
• a₁ = 1.65; a₂ = 0.5; a₃ = 0.3; a₄ = 1.0 – коэффициенты

Для формулы должны использоваться единицы измерения в системе СИ, результат вычислений (жёсткость) при этом будет в Н/м³.

Передача сдвигающего усилия в опорном узле

Сдвигающее усилие, действующее в плоскости опорной плиты, может быть воспринято:

• Трением
• Противосдвиговым упором
• Анкерами

Пользователь может выбрать нужный вариант в настройках монтажной операции Опорная плита. Программа не позволяет использовать сразу несколько вариантов, однако EN 1993-1-8 – Cl. 6.2.2 и Fib 58 – Chapter 4.2 в определённых случаях разрешает передавать сдвиговое усилие через анкера и трение. В общем случае, пренебрежение трением при расчёте анкеров будет идти в запас, хотя в некоторых случаях это может привести к недооценке трещиностойкости бетона на стадии эксплуатации. Как правило, пренебрегать сопротивлением трения можно, если:

• толщина бетонного раствора превышает половину диаметра анкера,
• несущая способность анкера определяется близостью его расположения к краю фундамента (скалывание),
• Анкер предназначен для восприятия сейсмических нагрузок.

Комбинации с использованием противосдвигового упора не допускаются ни в каких случаях в виду совместности деформаций (в расчётной модели противосдвиговой упор заменяется полным одноузловым ограничением).

Восприятие усилия трением

Прочность на сдвиг определяется как коэффициент надёжности, помноженный на коэффициент трения (задаётся в Настройках) и на сжимающую нагрузку. При вычислении сжимающей нагрузки учитываются все нагрузки, то есть, в случае колонны, загруженной продольной силой и изгибающим моментом, величина, используемая в проверке на сдвиг, будет больше именно за счёт изгиба.

Восприятие усилия противосдвиговым упором

TПротивосдвиговой упор представляет собой профиль, погружённый в бетон под опорной плитой. Предполагается, что сдвигающее усилие распределяется по погружённому в бетонный блок профилю равномерно, то есть все узлы упора нагружены одинаково. Часть противосдвигового упора, находящаяся над поверхностью бетонного блока (в зазоре, заполненном раствором), нагрузки не воспринимает. Также следует помнить, что плечо между сдвигающей силой (приложенной в уровне опорной плиты) и отпором погружённого профиля может вызывать изгиб, который передаётся на анкера в виде растягивающих и сжимающих усилий.

Противосдвиговой упор разбивается на пластинчатые КЭ и проверяется как остальные пластины. Сварные швы крепления противосдвигового упора к опорной плите также проверяются по стандартной процедуре, реализованной в IDEA StatiCa Connection. В ручных расчётах противосдвиговые упоры обычно рассматриваются как балки, что не совсем корректно, так как отношение длины профиля к его ширине слишком мало. Поэтому результаты расчётов, сделанных в IDEA StatiCa Connection, могут отличаться от традиционных.

Восприятие усилия анкерами

Сопротивление сдвигу в этом случае определяется прочностью анкеров на срез. Поведение стали анкеров принимается упругопластическим, но разрушение бетона по всем формам считается идеально хрупким.

Analysis

Расчётная модель

Разработанный компонентный метод конечных элементов предоставляет возможность быстрого расчёта узлов практически любой формы и конфигурации.  Модель собирается из элементов, к которым прикладываются нагрузки, и монтажных операций (включая элементы усиления), которые служат для соединения элементов между собой. Не стоит путать «элементы» с «элементами усиления» (первое – Элемент, второе – Монтажная операция); при подрезке «элементы» крепятся к главной точке узла и могут деформироваться не так, как «элементы усиления». Возьмите за правило: всё

Расчётная модель узла строится автоматически. Пользователь не тратит время на создание КЭ-модели, он конструирует узел при помощи монтажных операций – см. рисунок ниже.

Монтажные операции/элементы, с помощью которых конструируется узел

Каждая монтажная операция создаёт в узле определённые элементы или производит некоторые действия – добавляет пластины, болты, сварные швы, вырезы, отверстия и т.д.

Несущий элемент и опоры

Независимо от конфигурации один элемент узла всегда назначается «несущим». Все остальные элементы считаются «присоединяемыми». Несущий элемент может быть назначен пользователем. Он может быть «Непрерывным» или «Конечным». Несущие элементы с типом «Конечный» всегда закрепляется с одного конца, а «Непрерывный» - с обоих концов.

Присоединяемые элементы могут быть различных типов, в зависимости от их характера работы и воспринимаемых усилий:

• Тип N-V_y-V_z-M_x-M_y-M_z – элемент может передавать все 6 компонентов внутренних усилий (н-р, несущий элемент пространственного каркаса).
• Тип N-V_y-M_z – элемент может передавать только нагрузки в плоскости XY, а именно N, V_y и M_z (балочные элементы, элементы плоских расчётных схем).
• Тип N-V_z-M_y – элемент может передавать только нагрузки в плоскости XZ – а именно N, V_z, M_y (балочные элементы, элементы плоских расчётных схем).  
• Тип N-V_y-V_z ­– элемент может передавать только поступательные нагрузки – всё, кроме моментов (связевые элементы каркасов, тонкие пластины)

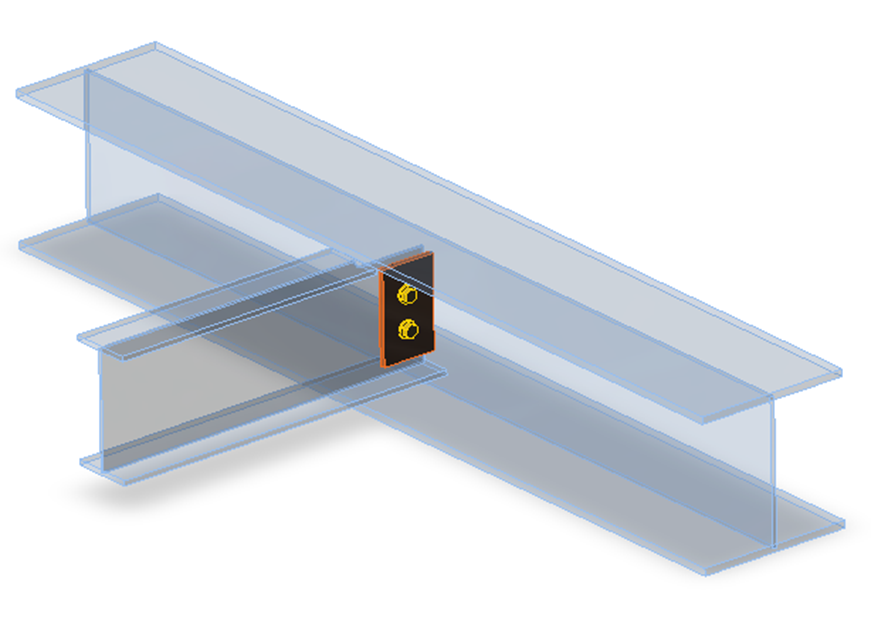
Стык балок на торцевых пластинах. Передаются все компоненты усилий

Планка на болтах. Передаются нагрузки только в плоскости XZ – усилия N, V_z, M_y

Связевой элемент – крепление решётки к колонне. Элемент B передаёт только поступательные усилия N, V_y и V_z

При статическом расчёте стержневой конструкции каждый её узел (место сопряжения элементов) находится в состоянии равновесия. Это условие должно соблюдаться и в КМКЭ модели при задании нагрузок на концах отдельных элементов. Поэтому задавать какие-либо опоры не обязательно – условия равновесия и так выполняются. Однако, из некоторых практических соображений, несущий элемент всё равно закрепляется в начале от всех перемещений (полная заделка). Это никак не сказывается на напряжениях и внутренних усилиях в элементах, а влияет только на вид деформированной схемы.

На конце каждого элемента задаются закрепления, соответствующие его типу. Это позволяет избежать геометрической изменяемости и некорректных результатов.

Длина каждого элемента по умолчанию принимается равной двум высотам сечения. Свободная длина элемента должна составлять не менее одной высоты его сечения от местоположения последней монтажной операции (сварного шва, отверстия, ребра жёсткости и т.д.). Это обусловлено тем, что на конце каждого элемента в месте его подрезки создаются жёсткие вставки, и если длина участка элемента до этой вставки будет слишком маленькой, то он будет деформироваться некорректно.

Равновесие узла

Каждый узел КЭ схемы в 3D должен находиться в равновесии. Данное требование логично и правильно, но для расчёта простых узлов соблюдать его не обязательно. Как уже говорилось, один из элементов узла всегда является «несущим», а остальные – «присоединяемыми». Если стоит задача только о проверке соединений узла – сварных швов, болтов, то условие равновесия можно не соблюдать. Это практически никак не скажется на коэффициентах использования анализируемых элементов (болтов и сварных швов). Поэтому в программе доступны два режима задания нагрузок (для версии 9.0 и новее есть отличия):

• Упрощённый – в этом режиме «несущий» элемент закрепляется с двух сторон, а нагрузки прикладываются только к «присоединяемым» элементам.
• Расширенный (более точный с проверкой равновесия). При этом «несущий» элемент закрепляется только с одного конца, а нагрузки могут быть приложены ко всем элементам узла. Условие равновесия нагрузок в узле проверяется программой.

Нужный режим можно задать в группе ленты Опции, щёлкнув на кнопку Равновесие нагрузок.

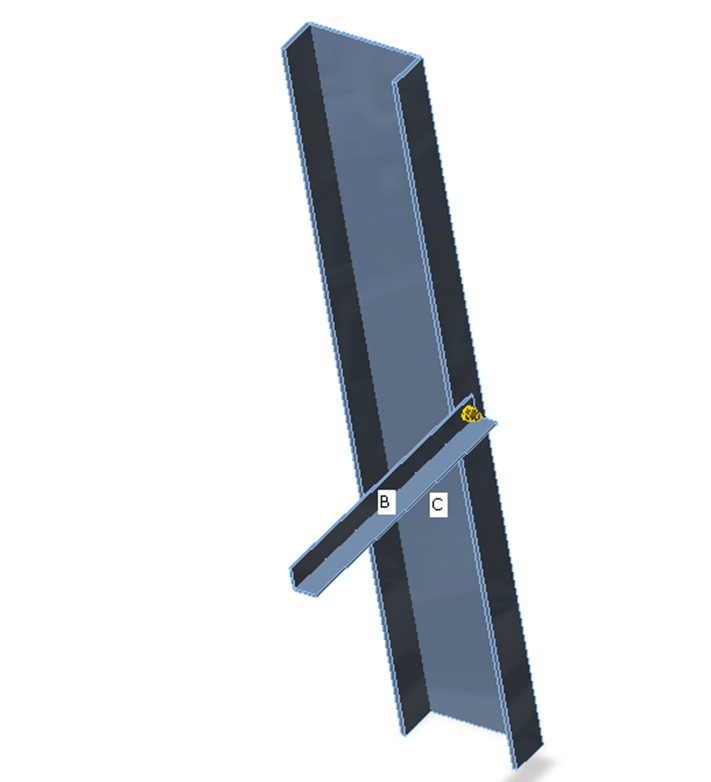
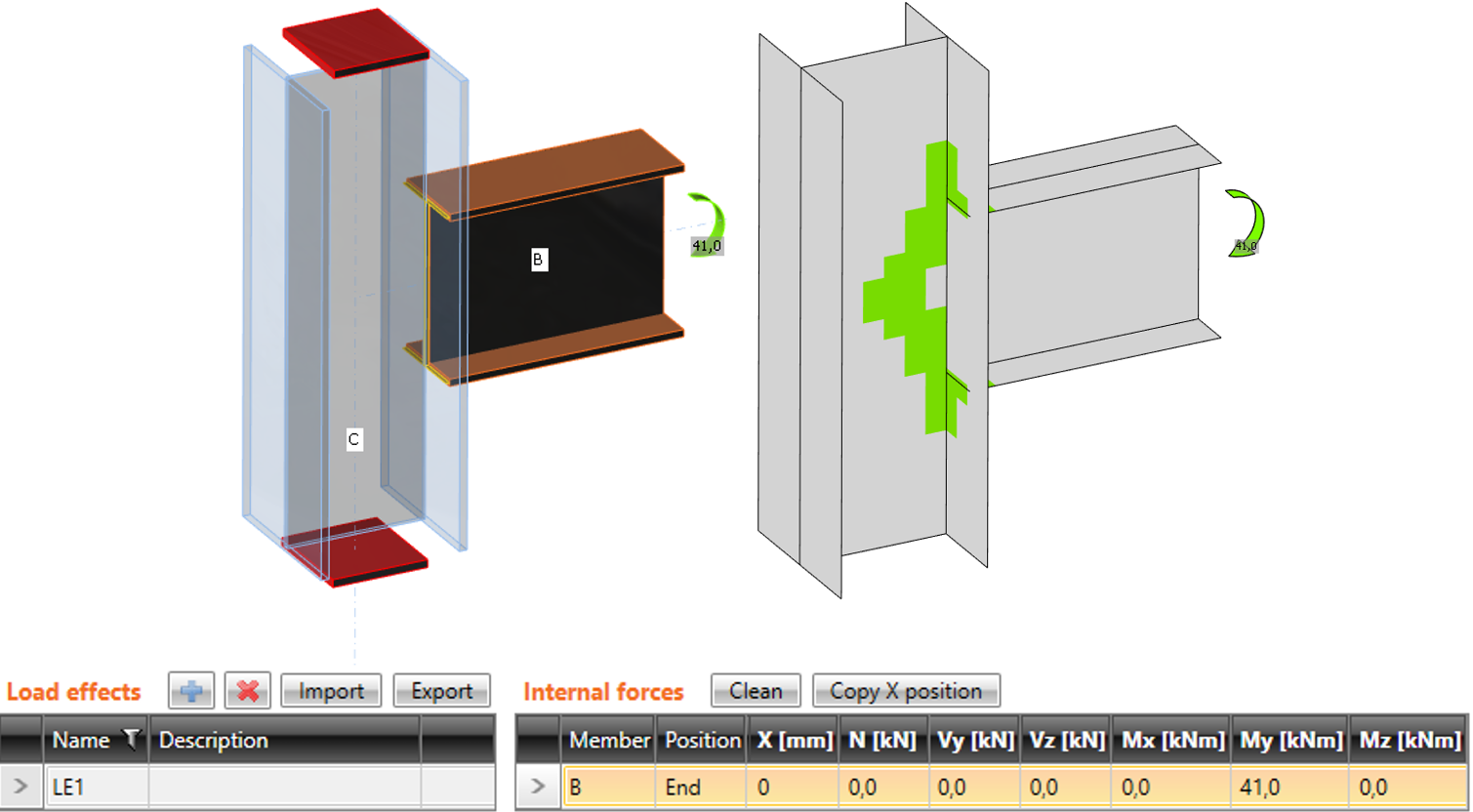
Различия при использовании двух разных режимов приводится ниже. В качестве примера рассматривается рамный узел – стык балки и колонны. К концу балки приложен изгибающий момент 41 кНм. Колонна испытывает действие сжимающей нагрузки в 100 кН. В случае упрощённого режима продольная сила в колонне не учитывается, так как она закрепляется с двух концов. Программа покажет только влияние изгибающего момента. Действие продольной силы можно оценить только в расширенном режиме.

Упрощённый режим: продольная сила в колонне НЕ учитывается

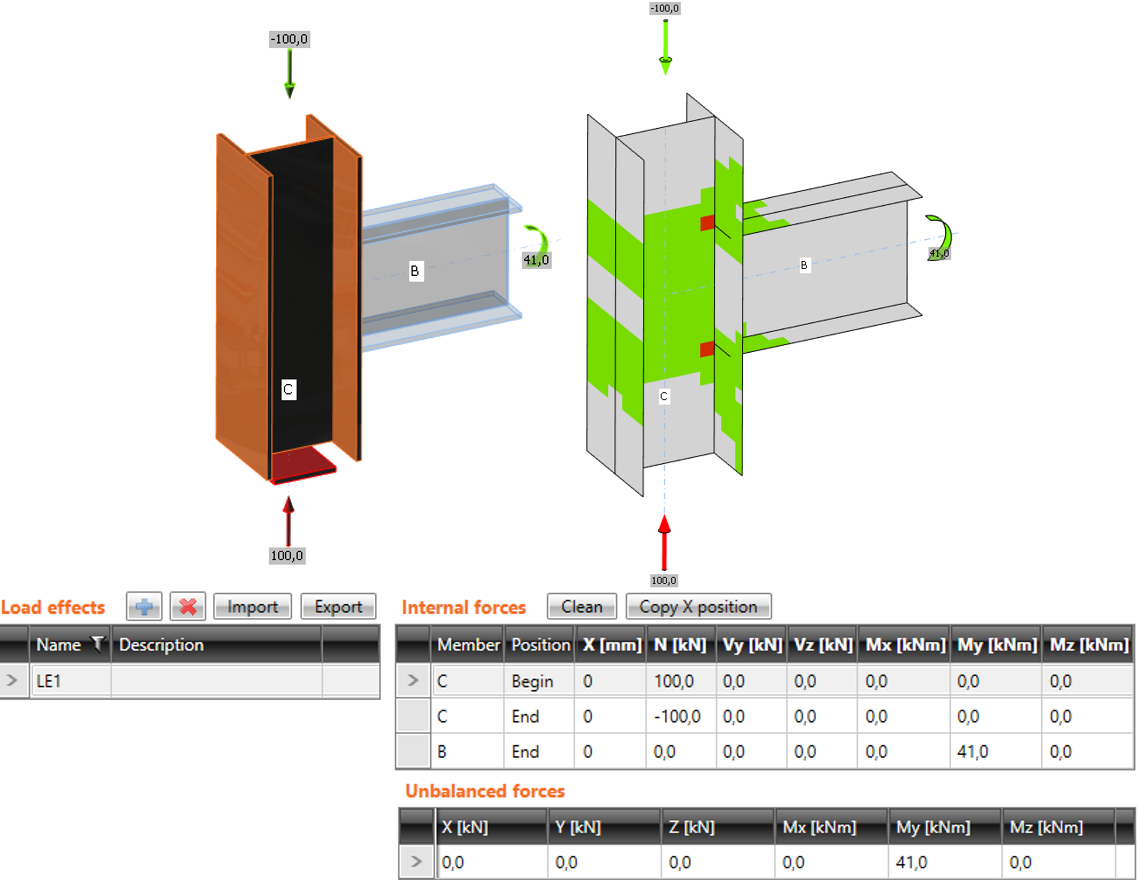
Расширенный режим: продольная сила в колонне учитываетсяУпрощённый режим более удобен для пользователя, но он подходит только для случая, когда анализируются отдельные элементы узла (болты, сварные швы), а не работа всего узла.

В случае, когда «несущий» элемент испытывает значительные нагрузки и напряжения в нём близки к предельным, необходимо использовать расширенный режим, задавая при этом соответствующие внутренние усилия.

Нагрузки

Усилия на концах элемента стержневой расчётной схемы приводятся к усилиям, приложенным к элементам сечения элемента в IDEA StatiCa. При приведении усилий учитываются эксцентриситеты отдельных элементов, вызванные конструкцией узла. 

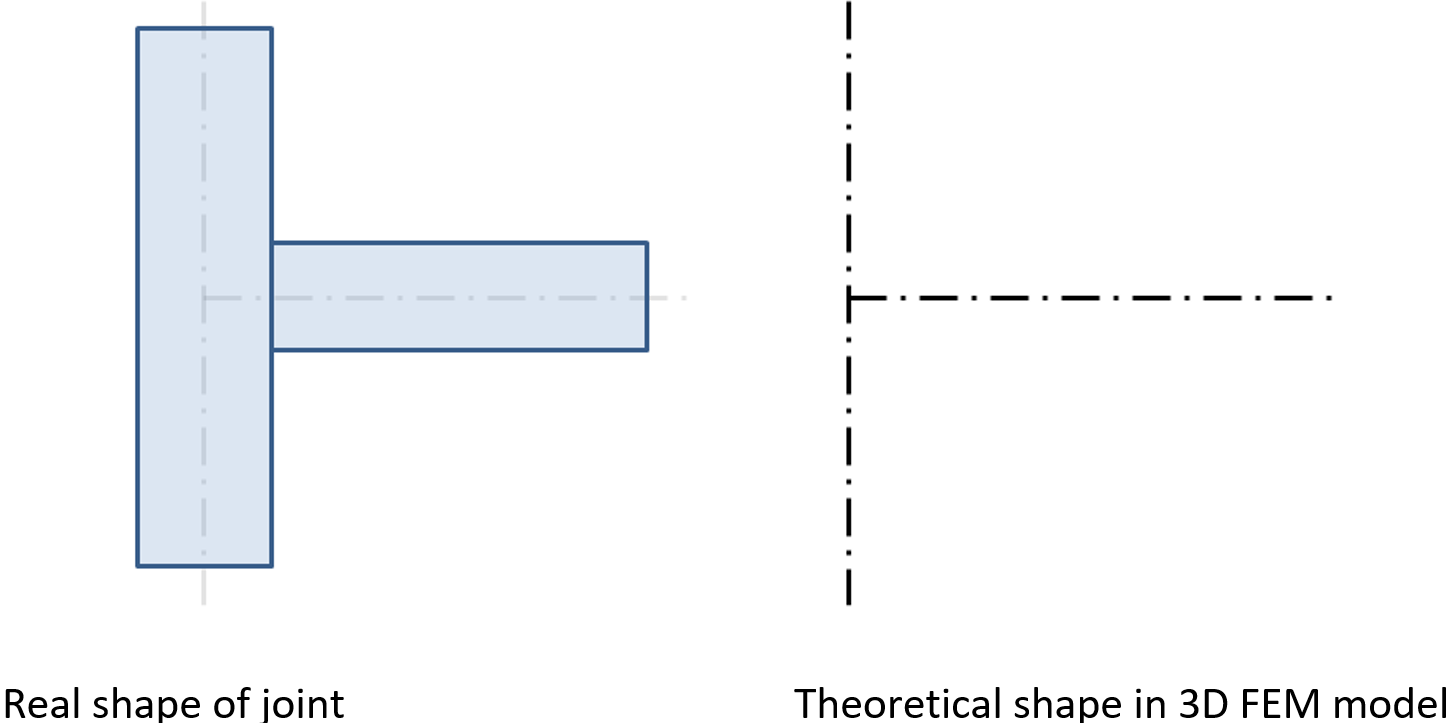
Расчётная КМКЭ-модель очень точно учитывает реальную форму узла, в то время как величины внутренних усилий берутся из идеализированной КЭ пространственной стержневой схемы, в которой балки и колонны моделируются просто осевыми линиями, а узлы – сопряжения этих элементов – просто узлами, не имеющими размеров.

Узел стыка балки с колонной. Реальная форма узла и его теоретическая КЭ модель

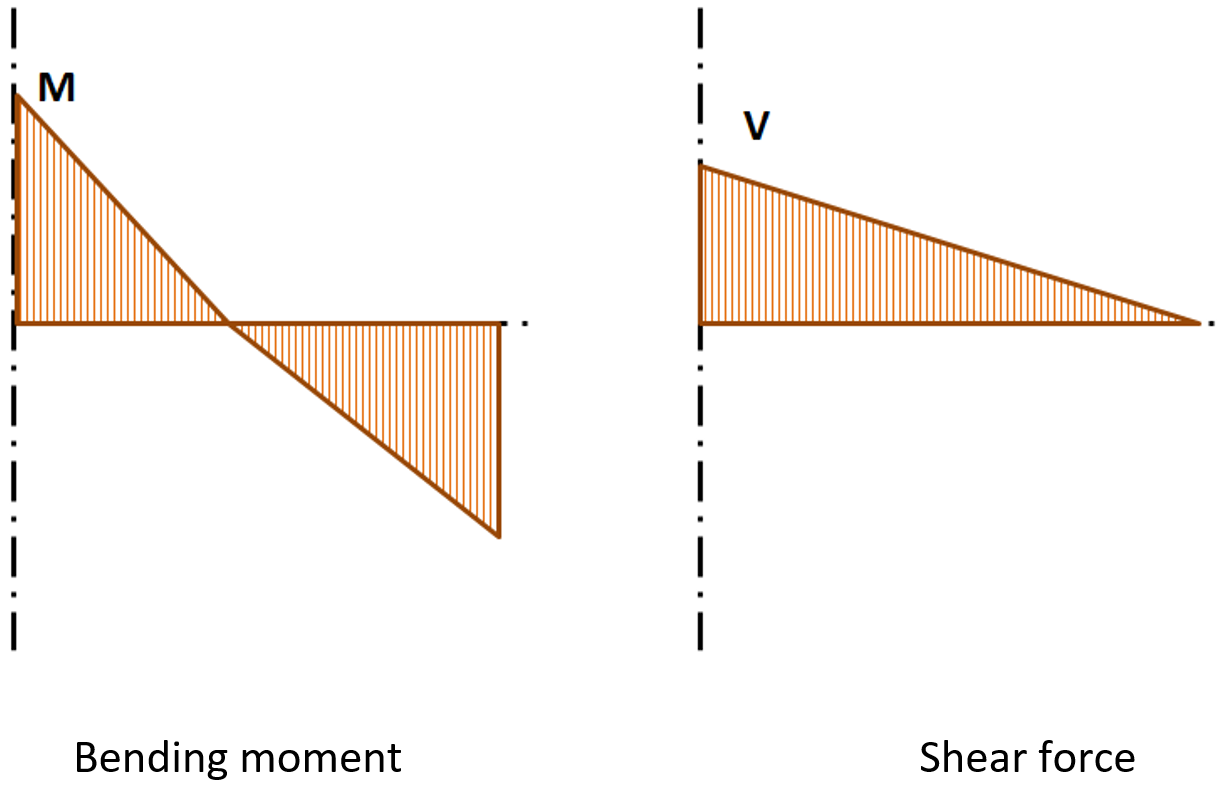
Внутренние усилия находятся в пространственных стержневых элементах. Ниже приводится пример – эпюры внутренних усилий в стержневом элементе.

Эпюры изгибающего момента и поперечной силы в балке. M и V – величины усилий в узле

При конструировании и расчёте узла (соединения) важно учесть его реальные размеры. Это в свою очередь влияет на процедуру задания нагрузок – см. поясняющие рисунки ниже:

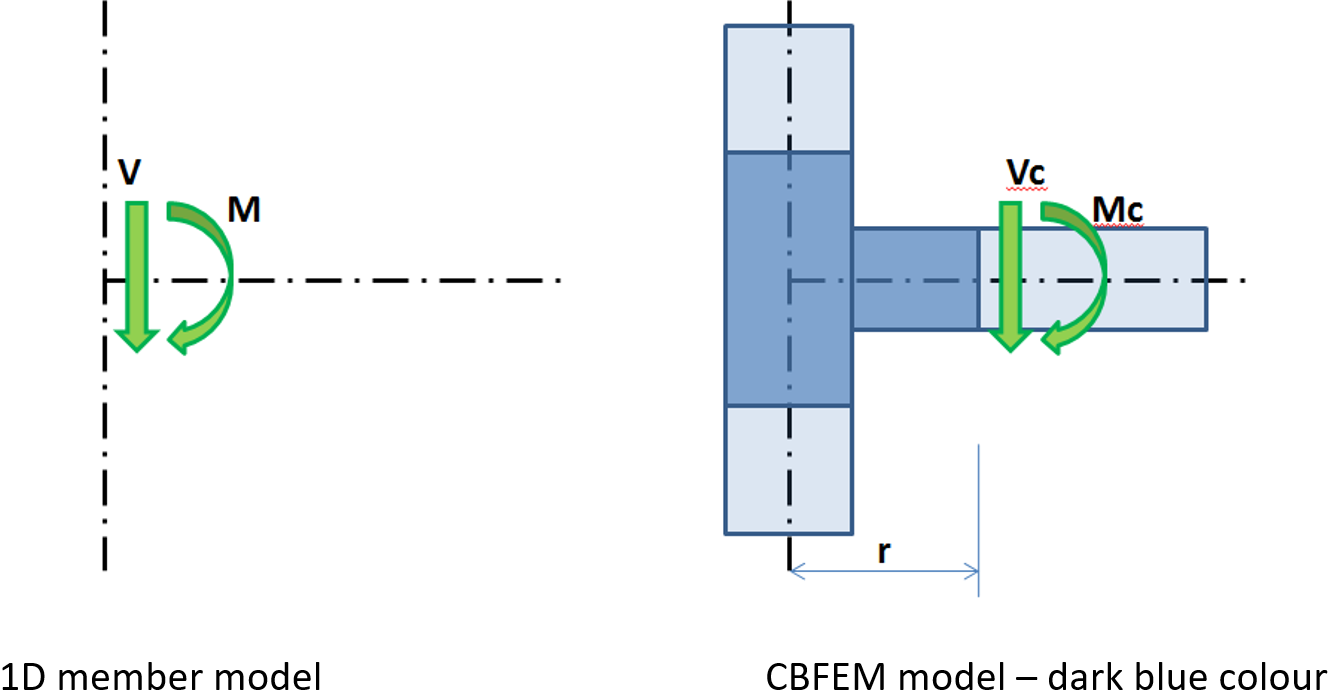
Влияние реальных размеров узла на нагрузки в КМКЭ модели (выделена тёмно-синим цветом)

Изгибающий момент М и поперечная сила V действуют в теоретическом узле. Эта точка – теоретический узел, в КМКЭ модели фактически не существует. Следовательно, в ней не могут быть заданы нагрузки. Их можно приложить только к концам элементов, но значения этих нагрузок должны быть пересчитаны с учётом реальных размеров элементов узла – расстояний r (от конца элемента до т.н. теоретического узла)

M_c = M – V ∙ r

V_c = V

IКМКЭ модель узла оперирует именно усилиями, приложенными к торцам элементов – M_c и V_c, несмотря на то, что в загружениях задаются именно усилия из стержневой модели - M и V.

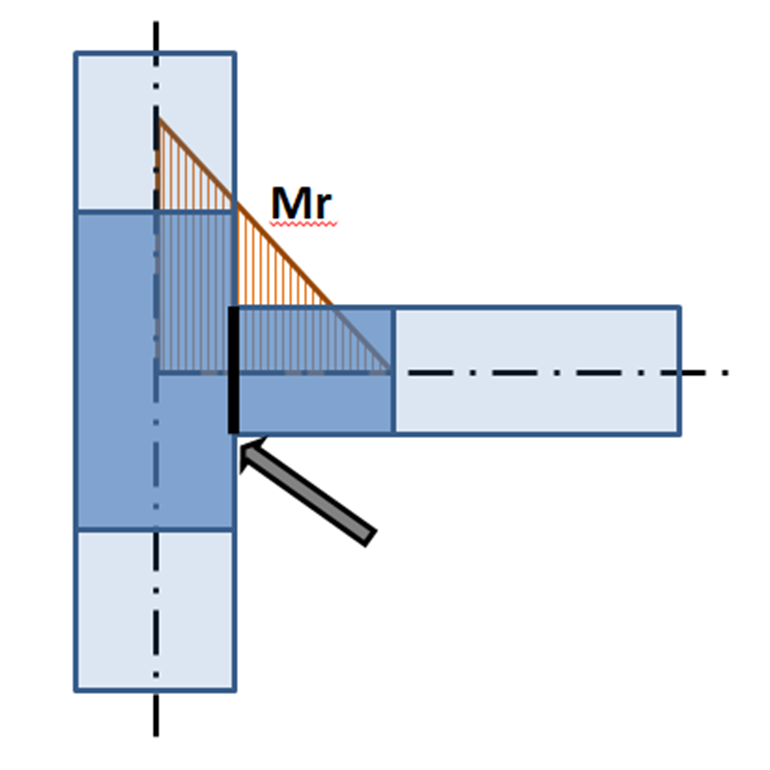
При расчёте и конструировании узла необходимо также учитывать его реальное положение в составе конструкции относительно теоретического узла. Обычно внутренние усилия, действующие в реальном узле, отличаются от усилий, действующих в теоретическом узле. Благодаря использованию точной КМКЭ модели расчёт соединений производится на заниженные значения усилий – см. рисунок с эпюрой M_r:

Эпюра изгибающего момента в КМКЭ модели. Стрелка указывает на фактическое расположение стыка элементов

При задании нагрузок необходимо понимать, что реальная конструкция узла должна соответствовать принятой ранее теоретической модели с точки зрения внутренних усилий. Для жёстких соединений всё кажется довольно очевидным – внутренние усилия идентичны, но в случае шарнирных узлов есть существенные различия.

Положение шарнира в теоретической КЭ модели 3D узла и его фактическое положение в реальной конструкции (КМКЭ модели)

Предыдущий рисунок как раз демонстрирует различия в положении шарнира в стержневой КЭ модели и в реальной конструкции узла. Следует помнить, что любая теоретическая модель в полной мере не соответствует реальности. При приложении к узлу вычисленных значений внутренних усилий (см. рисунок выше), в шарнире возникнет существенный изгибающий момент (шарнир смещен относительно теоретического узла). В этом случае узел будет перегружен или же вовсе не сможет быть рассчитан. Решение данной проблемы весьма простое – модели должны согласоваться друг с другом. Либо шарнир будет задаваться в нужном положении в КЭ стержневой модели, либо же эпюра внутренних усилий будет смещаться в сторону до тех пор, пока изгибающий момент в шарнире не станет нулевым.

Смещённая эпюра изгибающего момента в балке: момент в шарнире нулевойСмещение эпюр может быть задано в таблице задания внутренних усилий (в версии 9.0 и новее это задаётся в свойствах самого элемента).

Положение заданных внутренних усилий оказывает большое влияние на правильность результатов расчёта. Во избежание недоразумений пользователь сам может выбрать место приложения усилий – Узел/ Болты / Позиция. Второй вариант предназначен для тех случаев, когда болты перпендикулярны оси элемента и физически пересекают какой-либо из его элементов сечения.  

Варианты приложения усилий – в узле, в болтах, в заданной позиции

Обратите внимание на то, что при выборе опции «Узел» для задания положения нагрузок, усилия будут прикладываться в начале выбранного элемента, которое, как правило, находится в главной (теоретической) точке узла, если только вручную не было задано смещение этого элемента.

Импорт нагрузок из сторонних КЭ-программ

IDEA StatiCa при импорте из сторонних КЭ-программ считывает из них результаты расчётов (внутренние усилия, деформации, реакции). Также считывается информация по комбинациям. Список и содержание комбинаций отображаются в мастере (или же BIM приложении).

При расчётах в КЭ программах обычно работают с огибающими комбинациями. В IDEA StatiCa Connection узлы стальных конструкций рассчитываются в нелинейной постановке (модель материал конструкций – упругопластическая). Это значит, что использовать огибающие комбинации в данном случае нельзя, так как они являются совокупностью линейных расчётов. При расчёте в IDEA StatiCa определяется наихудшее сочетание внутренних усилий (N, V_y, V_z, M_x, M_y, M_z) из всех заданных комбинаций усилий, приложенных к концам элементов, сходящихся в узле. Для каждого экстремального значения также определяются соответствующие значения внутренних усилий, приложенных к остальным элементам. Это сочетание усилий и используется как загружение при моделировании узла в IDEA StatiCa Connection.

Пользователь может при желании вносить изменения в список загружений. Он может работать с загружениями в специальном мастере (или BIM-связке) или же может удалить некоторые из загружений непосредственно в IDEA StatiCa Connection.

Внимание!

При импорте обязательно нужно контролировать равновесие нагрузок, действующих в узле. В следующих случаях можно получить несбалансированные усилия:

• В импортируемой схеме имеются нагрузки, приложенные к рассматриваемому узлу как сосредоточенные. Программа может не понять, какому из элементов следует воспринимать эту узловую нагрузку, и проигнорирует её в расчётной модели.
  Возможное решение: Не прикладывайте узловых нагрузок при расчёте всей конструкции. При необходимости усилие может быть вручную назначено выбранному элементу как продольная или поперечная сила.
  
• К рассматриваемому узлу крепится неметаллический (обычно бетонный или деревянный) элемент, воспринимающий нагрузку. Такой элемент не участвует в расчёте и усилия в нём не будут учитываться.
  Возможное решение: замените рассматриваемый элемент бетонным блоком с анкерами. 
  
• Узел является частью какой-нибудь стены или плиты (обычно из ЖБ). Плита или стена не рассматриваются как часть расчётной схемы, и усилия в них будут проигнорированы.
  Возможное решение: замените плиту или стену бетонным блоком с анкерами.
  
• Некоторые элементы присоединяются к узлу при помощи жёстких вставок. Такие элементы не будут включены в модель, и усилия в них будут проигнорированы.
  Возможное решение: добавьте эти элементы в IDEA StatiCa вручную.
  
• В программе, из которой осуществляется импорт, производился расчёт на сейсмические нагрузки. Большинство программ на основе МКЭ для решения задач, связанных с сейсмикой, используют процедуру модального расчёта. Результаты внутренних усилий при расчётах на сейсмические нагрузки обычно представляются в виде огибающих по сечениям. Ввиду импользуемого метода расчёта (извлечение квадратного корня из суммы квадратов) все внутренние усилия будут положительными, а найти усилия, соответствующие заданному экстремальному значению. В этом случае внутренние усилия не будут находиться в равновесии.
  Возможное решение: знаки внутренних усилий можно изменить вручную.

Расчёт на прочность

Расчёт узла производится с учётом нелинейной работы материала. Нагрузка прикладывается пошагово, для каждого шага определяется соответствующее равновесное напряжённо-деформированное состояние (НДС). В IDEA Connection имеется два режима расчёта:

• Отклик конструкции (узла) на всю приложенную нагрузку. В этом режиме к узлу прикладывается вся заданная нагрузка (100%) и вычисляется результирующее НДС.

• Расчёт узла до наступления предельного состояния. В этом режиме ищется такое состояние узла, при котором все проверки ещё удовлетворяются, но дальнейший прирост нагрузки не возможен, так как при этом не будет выполняться одна из проверок (или несколько сразу). В случае, когда нагрузка превышает расчётную несущую способность узла, расчёт помечается красной меткой, а в статусе отображается процент приложенной нагрузки.

Второй режим более полезен в практическом использовании. Первый – лучше подходит для детального анализа сложных узлов.

Расчёт жёсткости и деформативности

Узлы можно классифицировать на жёсткие, полужёсткие и шарнирные в зависимости от их деформативной способности. При глобальном расчёте инженер-конструктор должен быть уверен в том, что принятые им гипотезы о жёсткости/шарнирности узлов соответствуют их реальной работе.

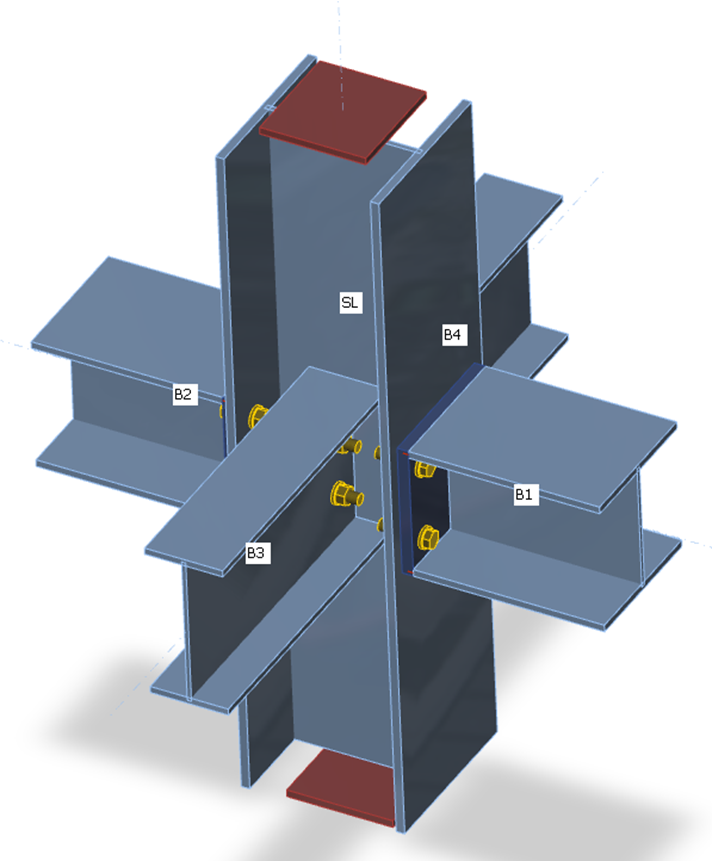
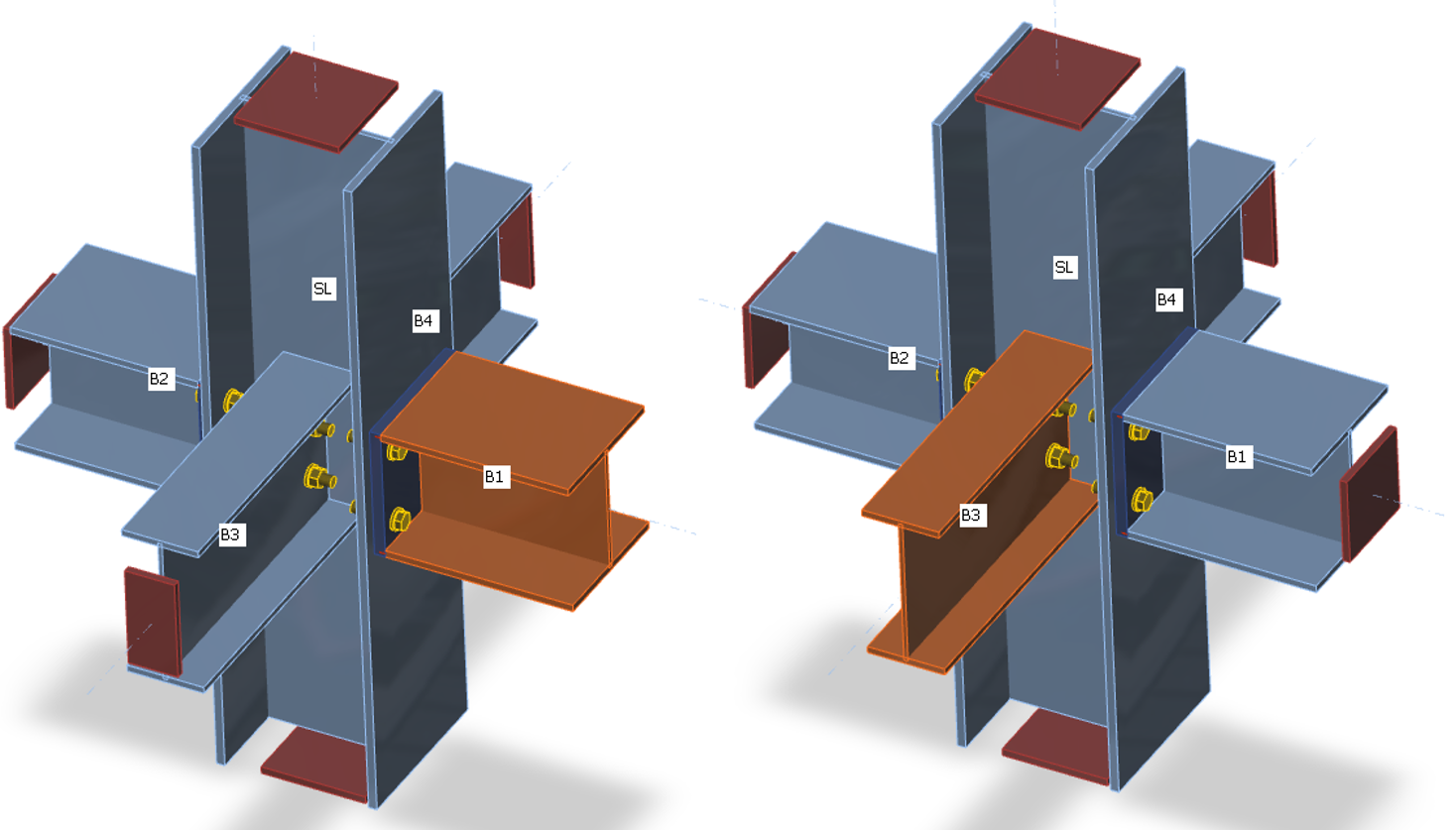
При помощи КМКЭ можно оценивать жёсткость прикрепления отдельных элементов узла. Для правильного расчёта жёсткости необходимо создать отдельные расчётные модели для каждого исследуемого элемента. На жёсткость прикрепления отдельного элемента не влияет жёсткость других, а влияет сам узел и способ присоединения к нему этого элемента. Если при расчёте прочности (элемент SL на рисунке ниже) закрепляется только «несущий» элемент, то при расчёте жёсткости закрепляются все элементы, кроме рассчитываемого (ниже приводятся рисунки – для расчёта прочности и для расчёта жёсткости элементов B1 и B3).

Закрепления элементов при расчёте на прочность

Закрепления элементов при расчёте жёсткости элемента B1

Закрепления элементов при расчёте жёсткости элемента B3

Нагрузки в этом режиме могут быть приложены только к рассчитываемому элементу. Если задаётся изгибающий момент M_y, то анализируется вращательная жёсткость относительно
оси Y. Если будет задан M_z – вращательная жёсткость относительно оси Z. Если приложить к элементу продольную силу, программа отобразит график продольной жёсткости.

График жёсткости программа строит автоматически, он отображается в графическом окне и может быть добавлен в отчёт.  Графики вращательной жёсткости или поступательной продольной жёсткости могут быть построены для конкретной величины нагрузки. IDEA StatiCa Connection также может выполнять эту процедуру с учётом влияния других внутренних усилий.

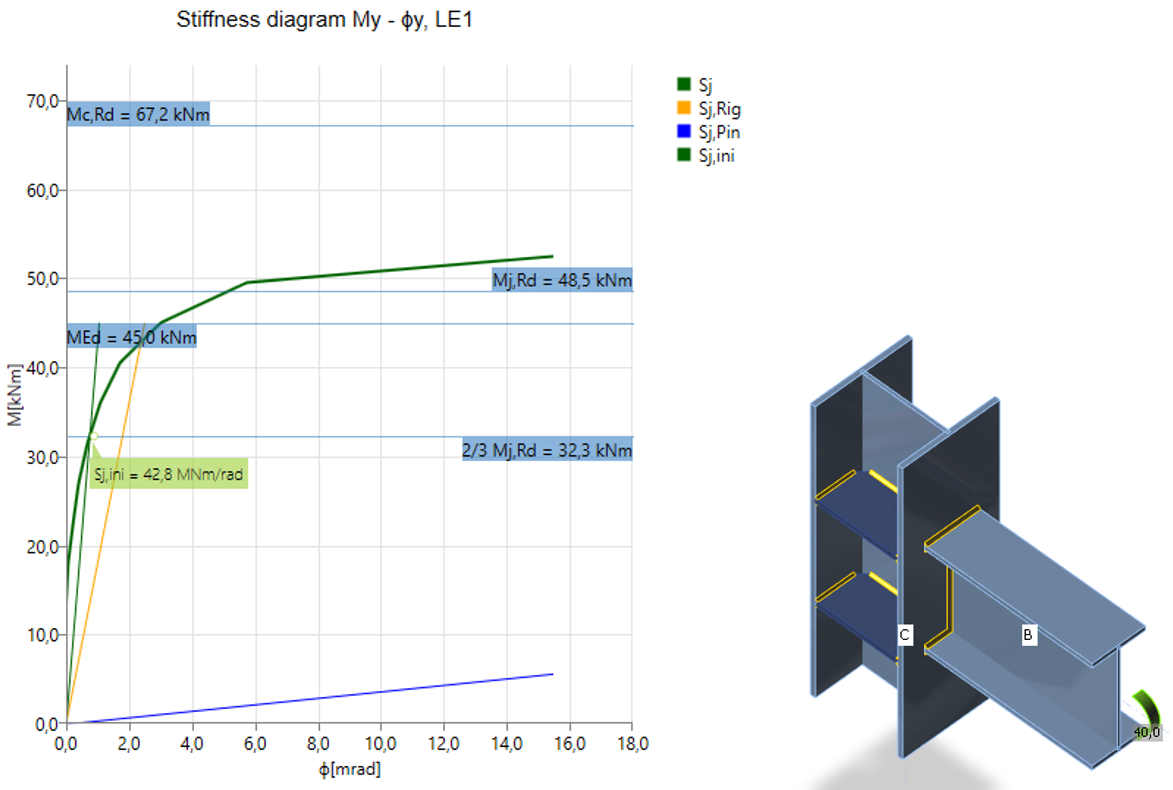
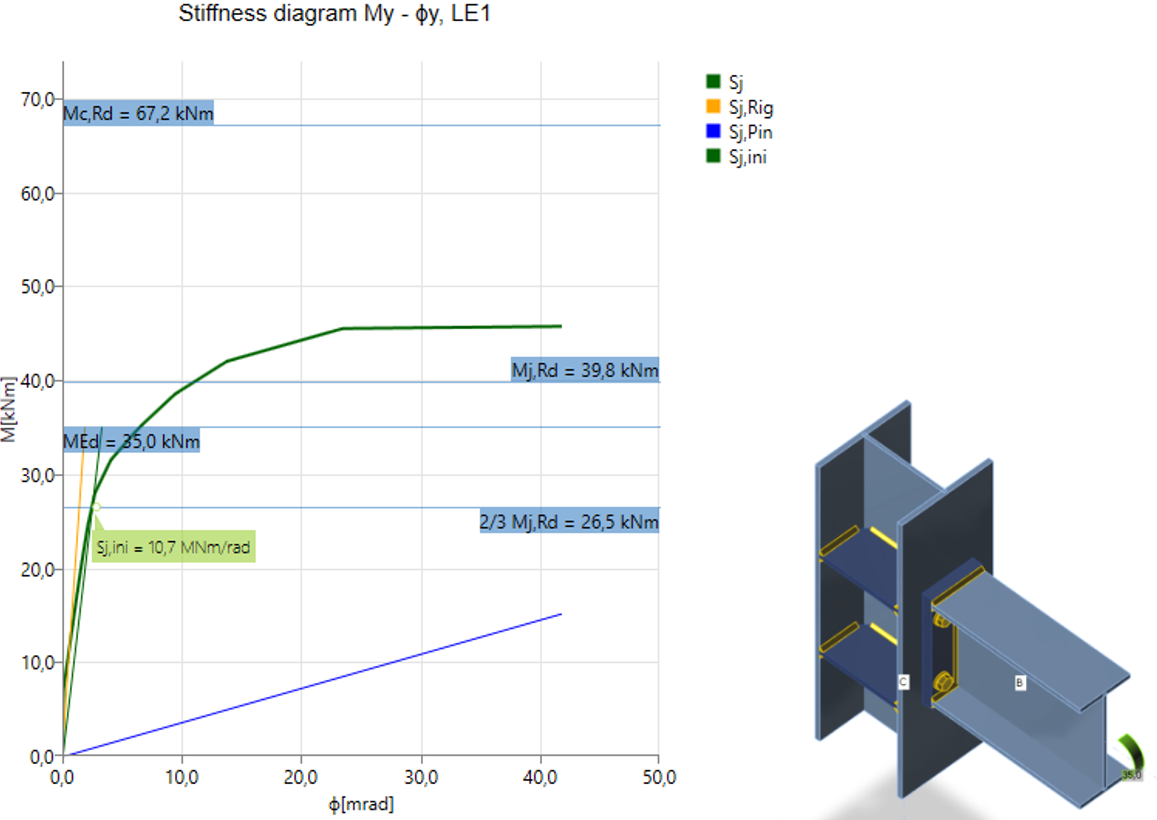
На графике отображаются:

• Уровень расчётной нагрузки M_Ed
• Предел несущей способности соединения при 5% эквивалентной деформации M_j,Rd; предельное значение пластической деформации может быть изменено в Настройках норм и расчётов
• Предел несущей способности элемента (подходит также для сейсмостойкого проектирования) M_c,Rd
• 2/3 предела несущей способности для расчёта начальной жёсткости
• Величина начальной жёсткости S_j,ini
• Величина секущей жёсткости S_js
• Граничные значения, по которым можно разделить узлы на группы – жёсткие и шарнирные
• Угол поворота Φ
• Предельный угол поворота Φ_c

Жёсткий узел на сварке

Полужёсткий узел на сварке и болтах

После достижения 5% деформации в стенке колонны при сдвиге развитие пластических деформаций идёт быстрее

Узлы классифицируются по их жёсткости на жёсткие, полужёсткие и шарнирные в зависимости от заданных норм. Для рассчитываемого элемента можно задать теоретические длины в плоскостях XOZ и XOY:

Под теоретической длиной здесь подразумевается пролёт балки в метрах до ближайшего раскрепления от перемещений по заданному направлению

Предельная деформативность

Предельная деформативность/пластичность δ_Cd относится к понятиям прочности и жёсткости, которые в совокупности описывают работу соединения. В рамных узлах пластичность достигается за счёт значительного предельного угла поворота φ_Cd (предельного угла поворота). Предельные значения деформативности/угла поворота вычисляются для каждого соединения отдельно друг от друга. 

Оценка предельного угла поворота ­– особенно важный вопрос при конструировании узлов, подверженных сейсмическим нагрузкам: см. (Gioncu and Mazzolani, 2002) и (Grecea 2004), и экстремальным нагрузкам: см. (Sherbourne AN, Bahaari, 1994 and 1996). Вопросами изучения предельной деформативности элементов стальных узлов занимаются уже с конца предыдущего века (Foley and Vinnakota, 1995). Faella и другие (2000) проводили эксперименты на Т-образных фланцах и аналитически выводили зависимости для предельной деформативности. Kuhlmann и Kuhnemund (2000) проводили тесты применительно к стенке колонны, подверженной поперечному сжатию, при различных уровнях продольной силы в колонне.   Da Silva и другие (2002) исследовали предельную деформативность при различных значениях продольной силы в прикрепляемой балке. На основании результатов экспериментов в сочетании с КЭ расчётом (Beg и другие, 2004) были получены значения предельной деформативности по основным аналитическим моделям. В данной работе компоненты представлялись нелинейными пружинами, объединёнными соответствующим образом. С помощью такой модели определялась предельная деформативность рамных узлов, фланцевых соединений (с пластиной заподлицо и с болтами в верхней части) и соединений на сварке. Как оказалось, наиболее существенный вклад в предельную деформативность колонны вносят пружины, отвечающие за сжатие и растяжение стенки, её сдвиг, а также связи, моделирующие изгиб пояса колонны и изгиб торцевой пластины (фланца). Компоненты, относящиеся к стенке колонны, оказывают существенное влияние только в случае отсутствия рёбер жёсткости, которые берут на себя сжимающие, растягивающие и сдвигающие усилия. Наличие ребра жёсткости сводит к минимуму работу этого компонента (стенка колонны), и поэтому его влиянием на предельную деформативность можно пренебречь. Торцевые пластины (фланцы) и пояса колонны важно учитывать только при расчёте фланцевых соединений (крепление балки к колонне через торцевую пластину), где компоненты взаимодействуют по Т-образной схеме, в которой также учитывается деформативность болтов при растяжении. Girao и другие в 2004 году занимались вопросами изучения пределов деформативной способности соединений из высокопрочной стали.

Расчёт узла с учётом образования пластического шарнира

Данный расчёт является неотъемлемой частью процесса проектирования конструкций в сейсмоопасных регионах. Расчёт выполняется в том предположении, что в одном из элементов наблюдается появление пластического шарнира.

Цель расчёта с учётом пластического шарнира – подтверждение заложенного варианта пластического разрушения (механизма) для предотвращения неконтролируемого обрушения, возникающего при расчётном землетрясении.

Один из элементов назначается диссипативным, прочность которого будет выше, чем остальных, и диаграмма работы немного будет отличаться. Коэффициент переупрочнения \(\gamma_{ov}\) задаётся в Материалах, а коэффициент деформационного упрочнения \(\gamma_{sh}\) – в настройках свойств самого диссипативного элемента. Обращаем ваше внимание на то, что наименования коэффициентов и терминов могут варьироваться в зависимости от выбранных норм проектирования. Диссипативный элемент не включается в проверку пластин по пластическим деформациям. 

Модифицированная диаграмма работы диссипативного элемента

При расчёте IDEA StatiCa Connection проверяет узел на действие приложенной нагрузки, которая должна приводить к появлению пластического шарнира в выбранном диссипативном элементе, обычно балке. Уровень пластических деформаций в этом элементе обычно должен составлять около 5 %. Это может служить подтверждением правильного задания как положения нагрузок, так и их величины. 

Пластический шарнир, возникающий в характерном месте диссипативного элемента – балки

Опорные связи непрерывного элемента автоматически задаются с одной стороны – полным защемлением, а с другой - с запретом изгибающих моментов. В этом случае непрерывная колонна может быть нагружена продольной и поперечными силами, а также имеет возможность перемещаться в стороны, чтобы можно было отследить предельное состояние стенки колонны.  

Особенно важно в расчёте подобных узлов на сейсмическую нагрузку соблюдать конструктивные требования, которые для данного расчёта в IDEA StatiCa не проверяются. 

Расчёт предельной нагрузки для узла

Рассчитывая узлы, инженер, как правило, решает конкретную задачу – вычисление реакции узла, напряжённо-деформированного состояния, от известной нагрузки. Однако, зачастую бывает необходимо понимать, насколько это состояние близко к предельному. Другими словами, насколько велики резервы его несущей способности и безопасна его конструкция? Ответить на этот вопрос поможет режим «Расчёт предельной нагрузки».

Пользователь задаёт нагрузки в обычном режиме. Программа пропорционально увеличивает все компоненты нагрузки до тех пор, пока какая-нибудь из проверок не будет выполняться. К ним относятся:

• проверка пластин,
• проверка болтов – по прочности на срез, растяжение и их совместное действие,
• проверка анкеров – по срезу и растяжению
• проверка сварных швов.

В итоге пользователь получает коэффициент отношения максимальной приложенной нагрузки к заданной расчётной. По результатам расчёта строится простой и наглядный график. Для более точной оценки работоспособности узла рекомендуется выполнить поверочный расчёт в режиме Напряжения/Деформации (EPS). 

Результаты расчёта на заданное загружение отображаются, только если величины нагрузок не превышают расчётного сопротивления узла. В противном случае результат расчёта покажет коэффициент менее 100%. Это значит, что итерационный процесс не был завершён, так как нагрузка уже превышает предельную. При этом результаты отобразятся только для последней итерации.

Линейный расчёт устойчивости

Обычно линейный расчёт устойчивости не так важен для узлов. Однако, проверку можно выполнять для того, чтобы быть уверенным, что результаты прочностного расчёта (который геометрически линейный) корректны.

IDEA StatiCa Connection позволяет выполнять линейный расчёт устойчивости модели узла. В качестве результатов отображаются формы потери устойчивости. Критическая нагрузка, при которой происходит потеря устойчивости идеализированной модели, вычисляется для каждой формы. Величина этой силы представлена множителем к действующей в узле нагрузке. В соответствии с этими результатами пользователь может сам предусмотреть мероприятия для обеспечения надёжности конструкции.

Некоторые нормы проектирования, например, Еврокоды, рекомендуют опираться на коэффициент не менее 15 для стержневых моделей конструкций. Если критическая нагрузка превышает в 15 раз действующую, то, согласно нормам, выполнять проверку конструкций на устойчивость не обязательно.

Для узлов ситуация обстоит немного иначе, и нормы не дают особых рекомендаций. Вопрос местной устойчивости следует решать по-другому. Как правило, местная потеря устойчивости происходит в следующих частях конструкции:

1. Пластины, соединяющие отдельные элементы
2. Элементы жёсткости – рёбра, диафрагмы и короткие вуты
3. Замкнутые профили и тонкостенные сеченияПотеря устойчивости пластин из группы 1 влияет на форму потери устойчивости всего элемента. Поэтому рекомендуется применять к таким пластинам те же правила, что и к элементам, то есть, считать безопасными коэффициенты, равные или большие 15. При этом инженер должен следить за соответствием граничных условий модели узла, используемой для расчёта устойчивости, глобальной модели всей конструкции.

Пластины группы 2 влияют на местную потерую устойчивости в узле. Для таких пластин граничное значение коэффициента, равное 15, слишком консервативно, а в нормах отсутствуют чёткие рекомендации по этому случаю. Рекомендации могут быть взяты из результатов исследований, в ходе которых выяснилось, что для таких пластин коэффициента, равного 3, вполне достаточно. Потеря устойчивости пластин и элементов из группы 3 – самый сложный вопрос и требует индивидуальной проработки каждого случая.

Для пластин с коэффициентом, меньшим рекомендуемого значения (15 для группы 1, 3 для группы 2), пластический расчёт не применим. Для их проверки следует использовать другие методики, которых нет в IDEA StatiCa.

Результаты проверки узла в режиме «Устойчивость» совсем не похожи на привычные результаты проверок. Для таких случаев нормы не дают чётких рекомендаций. Оценка этих результатов требует серьёзных инженерных познаний. IDEA StatiCa обладает уникальным набором инструментов, которые не всегда есть в обычных программно-вычислительных комплексах, и будет вам надёжным помощником в решении сложных вопросов, связанных с устойчивостью.

Фасонка является продолжением трубы – пример пластины из группы 1, для которой минимальный коэффициент запаса равен 15

Примеры форм потери устойчивости пластин из 2ой группы, где минимальный коэффициент запаса равен 3

Модель, используемая для расчёта устойчивости, имеет граничные условия, отличающиеся от модели, используемой для расчёта НДС узла. Опорный элемент по-прежнему полностью закрепляется. Расчётная модель элемента N-Vy-Vz-Mx-My-Mz (в режиме НДС конец такого элемента полностью свободен от перемещений) соответствует полной заделке в режиме расчёта устойчивости. Все другие типы расчётных моделей ограничивают изгиб в двух плоскостях, но допускают поступательные перемещения по этим осям.

• Расчётная модель N-Vy-Vz-Mx-My-Mz:
  опоры в модели для оценки устойчивости по направлениям: N-Vy-Vz-Mx-My-Mz
• Расчётная модель N-Vy-Vz:
  опоры в модели для оценки устойчивости по направлениям: N-Mx-My-Mz
• Расчётная модель N-Vz-My:
  опоры в модели для оценки устойчивости по направлениям: N-Mx-My-Mz
• Расчётная модель N-Vy-Mz:
  опоры в модели для оценки устойчивости по направлениям: N-Mx-My-Mz

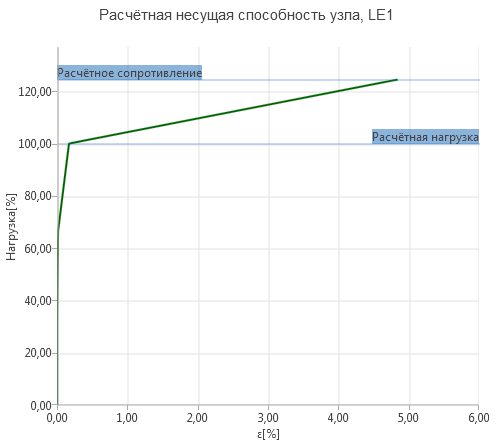
Предполагается, что в случае жёсткого узла пользователь задаёт изгибающий момент и устойчивость короткого участка балки не является столь значимым фактором. С другой стороны, в случае шарнирного узла пользователь задаёт только нормальную и срезающие силы без изгибающих моментов, но в этом случае потеря устойчивости элемента, примыкающего к узлу, будет критичной, так как это сильно влияет на коэффициент запаса устойчивости. Взгляните на картинки ниже. «Модель» - используется для анализа НДС узла, а «Устойчивость» — это модель для оценки устойчивости узла.

Сходимость расчёта

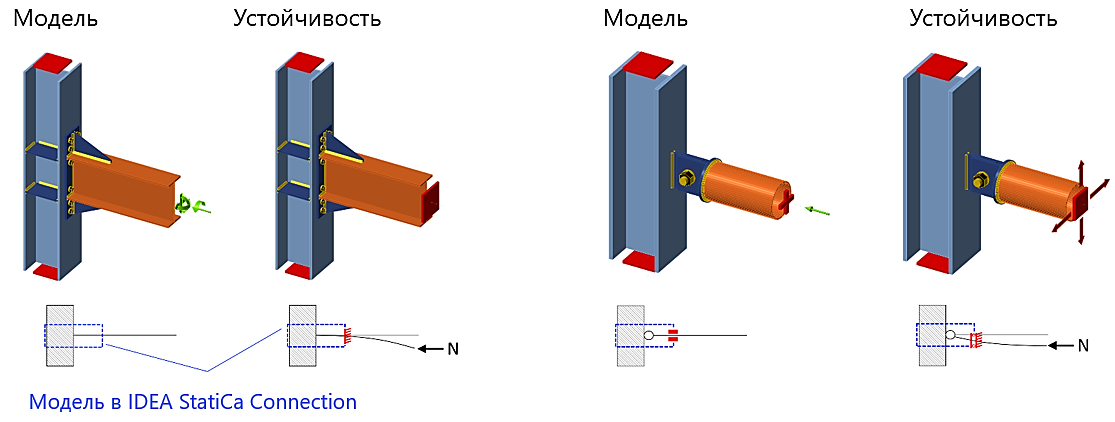
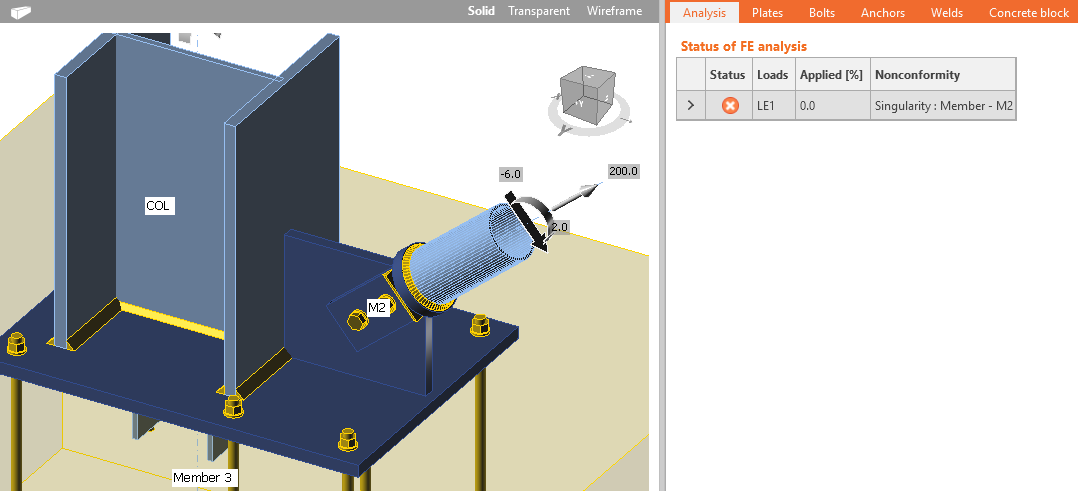
Для лучшей сходимости КМКЭ расчёта вторая ветвь диаграммы работы стали, отвечающая за пластическое деформирование, строится с небольшим наклоном. В некоторых случаях, особенно при работе со сложными моделями, в которых имеется большое количество контактных поверхностей, расчёт не всегда может сходиться к решению. В этом случае будет полезным увеличить количество расходящихся итераций (или количество итераций расчёта), это может решить проблему. Этот параметр может быть изменён в Настройках норм и расчётов. Наиболее распространённой ошибкой, не позволяющей завершить расчёт, является сингулярность матрицы жёсткости. Эта ошибка возникает, когда отдельные части модели не соединены должным образом друг с другом и имеют активные степени свободы (могут беспрепятственно перемещаться или поворачиваться). Чтобы проще было понять, где именно в модели возникла сингулярность, достаточно взглянуть на деформированную схему – незакреплённые элементы смещаются на 1 м относительно исходного положения.

Отсутствие сварных швов крепления фасонки к опорной плите приводит к сингулярности

Незакреплённый элемент смещается на 1м от заданного положения, позволяя быстро обнаружить сингулярность

Тонкостенные элементы

Программное обеспечение IDEA StatiCa Connection предназначено для анализа узлов из прокатных профилей, которые не сильно подвержены потере устойчивости. В программе реализован геометрически линейный и физически нелинейный расчёт в силу его быстроты и стабильности. Однако, этого расчёта может быть недостаточно в тех случаях, когда элементы узла теряют устойчивость. Когда потеря устойчивости оказывается серьёзной проблемой, расчёт устойчивости в линейной постановке как раз помогает выявить наиболее опасные области и получить коэффициенты запаса по Эйлеру (точки бифуркации). Но этого всё равно оказывается недостаточно при расчёте тонкостенных стержней. Их расчёт следует выполнять в геометрически нелинейной постановке с учётом начальных несовершенств.

Если вы всё-таки решили использовать IDEA StatiCa для расчёта соединений из тонкостенных профилей, вам следует:

• Выполнить линейный расчёт на устойчивость и досконально проанализировать каждую форму потери устойчивости, первых пяти форм может быть недостаточно.
• Не руководствуйтесь пластикой, возникающей в пластинах, скорее, наоборот, ограничьте напряжения по фон-Мизесу пределом текучести или даже меньшим значением.
• Помните, что местная потеря устойчивости, которая не учитывается, может привести к различному распределению внутренних усилий в компонентах.
• Не забывайте, что жёсткость компонентов может быть различной при различных формах потери устойчивости или их комбинациях.
• Помните, что отображаемые коэффициенты использования и результаты конструктивных проверок компонентов (болтов, сварных швов) вычисляются аналогично стандартным элементам. Эти же проверки для тонкостенных элементов могут отличаться, поэтому их результаты могут быть некорректными. 

Расчёт и проектирование соединений из тонкостенных элементов очень сложный вопрос, для которого нет общего подхода. Использовать IDEA StatiCa Connection в этой области не предполагалось.

Проверка компонентов – EN

В EN 1993-1-1 тонкостенные элементы определены следующим образом: «Класс 4 - сечения, в которых потеря местной устойчивости наступает до достижения предела текучести в одной или более зонах поперечного сечения». Основной раздел Еврокода для стальных конструкций ограничивает толщину элементов величиной t≥3мм, а глава 4 – использование сварных соединений – они применимы только к элементам с толщиной t≥4мм. Поэтому проверки компонентов, предоставляемые программой, не подходят для ЛСТК. Об этом нужно помнить и обязательно не забывать проверять такие элементы вручную по формулам из EN 1993-1-3.

Расчёту узлов из полых профилей также следует уделять пристальное внимание, особенно если они не описаны в таблице 7.1 EN 1993-1-8. Для этих случаев нет особых указаний, и тестирование IDEA StatiCa в этой области не выполнялось.

Проверка компонентов – AISC

В разделе А из AISC 360-16 имеется следующее примечание: «При расчёте и проектировании конструкций из ЛСТК (холодногнутых профилей) следует руководствоваться положениями документа AISI North American Specification for the Design of Cold-Formed Steel Structural Members (AISI S100), за исключением сечений из ЛСТК (HSS), которые были запроектированы в соответствии с данным документом». А в документах AISI S100 и AS/NZS 4600 приводятся формулы для проверки прочности на срез и растяжение наиболее часто используемых типов крепежа вместе с областями их применения.

Проверка компонентов – CISC

В Главе 1 CSA S16-14 говорится: “Требования к стальным конструкциям, таким как мосты, антенные мачты, морские сооружения и конструкции из холодногнутых профилей приводятся в других документах CSA Group Standards (Стандартах группы CSA)”.

Узлы из элементов замкнутого профиля (труб)

Узлы из тонкостенных профилей могут подвергаться серьёзным деформациям, но при этом допуская прирост нагрузки. С другой стороны, их отдельные стенки могут терять устойчивость в неупругом диапазоне. Для решения подобной проблемы был реализован физически и геометрически нелинейный расчёт.

Деформации из плоскости

Одним из критериев наступления предельного состояния в подобных узлах является деформация трубы из плоскости. Эта проверка реализована в программе (в Настройках норм за это отвечает чек-бокс «Проверка локальных пластических деформаций», он по умолчанию активен для моделей узлов, в которых несущим элементом выбрана труба). Это описано в нормах CIDECT. Предельные значения составляют составляют 3 % от меньшего размера сечения (0.03 d0 для круглых труб и 0.03 b0 для прямоугольных труб) для первого предельного состояния и 1 % для второго предельного состояния.

Размеры сечений для круглых и прямоугольных труб, используемые в проверках

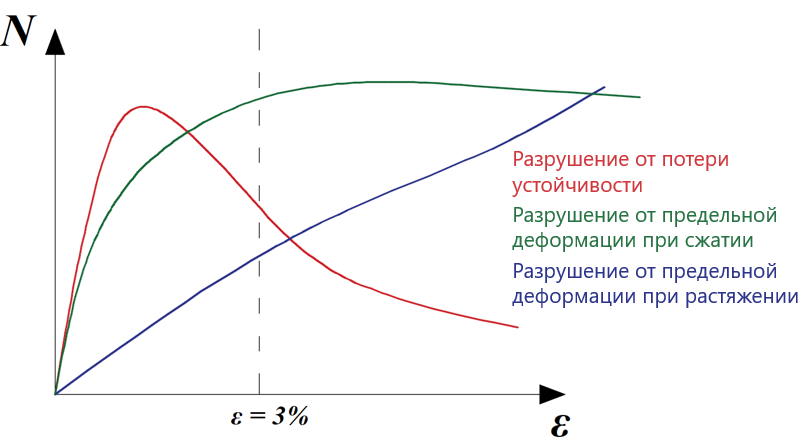
Характерные для узлов из труб диаграммы работы; красная кривая соответствует тонкостенным (гибким) элементам, подверженным сжатию, зелёная – обычным элементам при сжатии, голубая – Х-образным узлам, подверженным растяжению

Геометрически и физически нелинейный расчёт (ГФНР)

Для некоторых узлов из труб, особенно в случаях, когда отношение диаметра (высоты стенки) к толщине очень велико, геометрически линейный расчёт может не давать полное представление о работе узла, а прочность таких конструкций может быть завышена либо занижена. В подобных случаях для узлов из труб (или тонкостенных профилей) рекомендуется использовать более продвинутый геометрически и физически нелинейный расчёт, даже несмотря на большие затраты машинного времени. Если в Настройках норм активен чек-бокс Геометрическая нелинейность (ГНЛ), то расчёт моделей, в которых опорный элемент имеет сечение трубы, будет выполняться как с учётом физической, так и с учётом геометрической нелинейности (по умолчанию в IDEA StatiCa Connection активна только физическая нелинейность, ФНЛ).